基于高频热压成型的竹集成材制备及力学性能评价*

刘延鹤 周建波,2 傅万四 张 彬,2 常飞虎 何 文

(1. 国家林业和草原局北京林业机械研究所 北京 100029； 2. 中国林业科学研究院林业新技术研究所 北京 100091； 3. 南京林业大学材料科学与工程学院 南京 210037)

木材是国民经济发展的战略资源，在可持续发展战略实践中发挥着重要作用。当前，我国木材资源相对匮乏，各种木材和木制品需求越来越大，木材资源供不应求的现象越来越明显，寻找新的木材替代品迫在眉睫。竹子被认为是一种可以很好替代木材的 “绿色”原材料。我国竹林面积、竹材蓄积量均居世界首位，同时竹材强度、硬度、刚度高，生产周期短，作为性质优良的可再生材料具有广阔的应用前景(江泽慧等， 2005)。

竹集成材(glued laminated bamboo)是一种新型的竹制人造板，是竹材工业利用的主要方式之一(叶张柠， 2019； 李海涛等， 2016； 常飞虎等， 2018)。现行竹集成材大多采用多层热压成型加工(热压成型是竹单元或压坯在高温下的单轴向压制，从而激活扩散和蠕变现象)，工艺复杂，生产效率低，耗能高，所需模具数量多，使用寿命短； 也有少量竹集成材采用间歇冷压加工(间歇冷压是竹单元在室温、一定压力及器械下压制成具有一定形状、尺寸、强度、密度的坯体)，温度低，加工周期长，耗水量大，磨具损耗快。高频介质加热是在电磁波辐射下非导电物质分子(称为偶极子)反复极化振动和摩擦而发热，能耗低、加工速度快，是新时代很有潜力的新型能源之一(刘晓辉， 2018； 常飞虎等， 2018； 詹先旭等， 2018； 李文定等， 2014)。将高频介质加热技术引入到竹集成材加工中，将对竹材工业技术进步具有很大促进作用。竹材是一种多孔、低导热的天然复合材料，由纤维素、半纤维素、木质素以及少量有机物和无机物组成，受外部加热时，其内部升温速率较低。同时，竹材也是一种存在自由离子和束缚离子的介电物质，在细胞壁无定形区域有多种极性基团，如羟基等。此外，竹材还含有大量水分，当暴露在高频电场时，其中的分子将发生定向极化，竹材会迅速升温。竹坯作为加热介质，置于平行金属板间，当高频发生器工作时，正负板间形成高频交变电磁场，竹材中的极化分子和水分子会按电场方向被极化排列，随电场剧烈振动和摩擦而发热，用于蒸发水分并提高温度，促使胶黏剂快速凝固，缩短加工时间，提高生产效率(Weietal.， 2020； Xuetal.， 2019； Xuetal.， 2018； Muhammadetal.， 2018)。

热压温度和热压压力对竹集成材力学性能影响较大，同时高频介质加热也受竹材含水率和施胶量的影响。鉴于此，本研究以竹材含水率、热压压力、施胶量和热压温度为试验因子，探索4个参数变量对高频热压成型竹集成材力学性能的影响，并优化高频热压加工工艺获得力学性能较优的竹集成材，以期为竹集成材高频热压成型提供技术参考。

1 材料与方法

1.1 试验材料

竹条采自湖南省益阳市海利宏竹业有限公司，原材料为当地3～5年生毛竹(Phyllostachysedulis)，经定段、破竹、粗铣和干燥等工序后，精铣制成450 mm(长)×20 mm(宽)×5 mm(高)标准竹片。将竹条含水率分别调整为6%、9%、12%和15%，并按8个(长)×1个(宽)×4个(高)组坯(图1)，根据表1所示参数施胶。选用浙江诸暨光裕竹业有限公司生产的酚醛树脂胶黏剂(PF)，其固体含量为50%，酚醛树脂与面粉配胶时按10∶1使用。

图1 竹条及竹坯

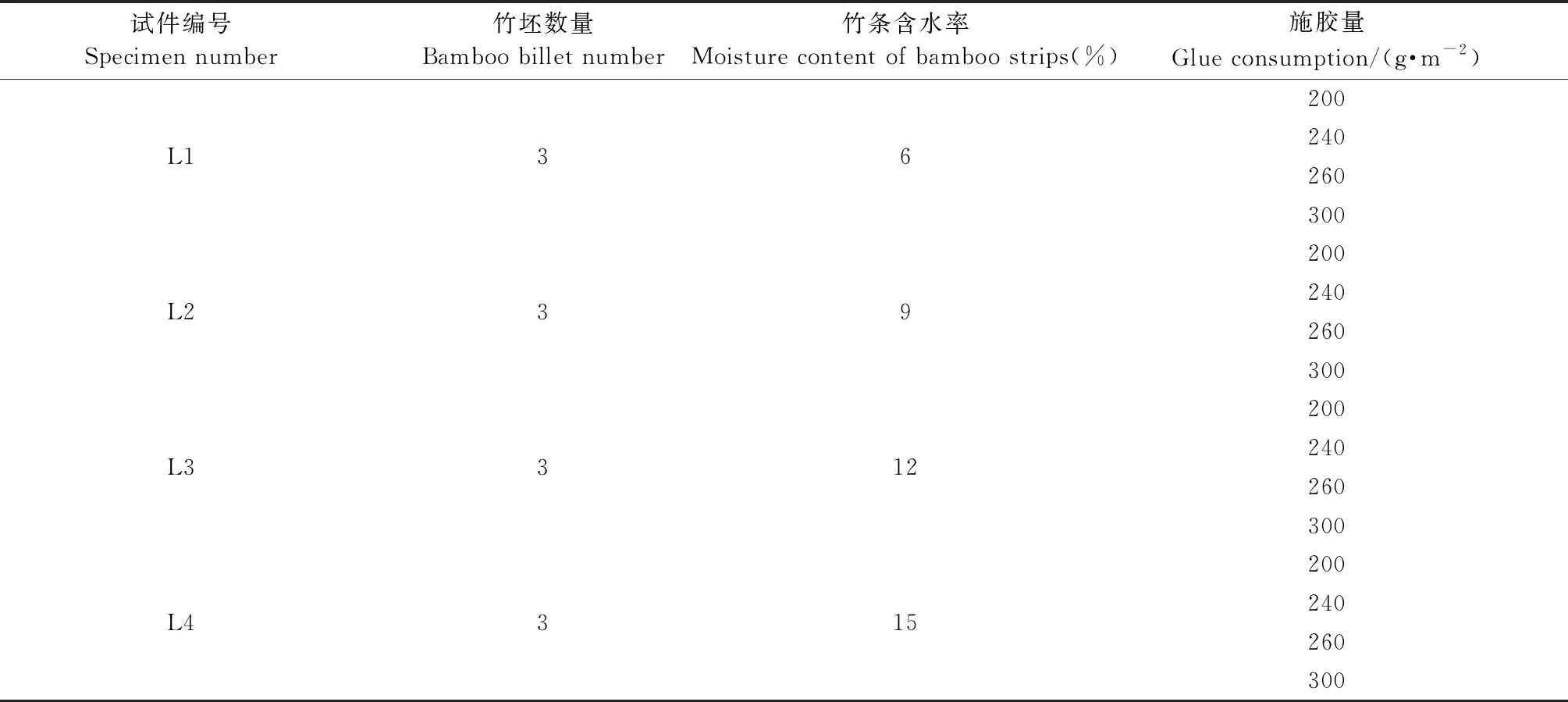
表1 竹坯试件及参数

1.2 热压参数及水平选择

采用河北省石家庄开发区纪元电气有限公司的GJ-15-6B-I型射高频发生器和GJB-PI-51B-JY型高频液压机(图2)，高频热压参数： 阳极电压Ua=5 kV、阳极电流Ia=2.0～3.0 A、栅级电流Ig=0.4～0.5 A、工作频率6.78 MHz(阮氏香江等， 2014； Nguyen等， 2015)，组坯完成的试件经高频热压加工成竹集成材。本研究考虑竹材含水率、热压压力、施胶量和热压温度4个参数变量对竹集成材力学性能的影响，热压参数及水平见表2(Kalawateetal.， 2017； Aydinetal.， 2005； Sharmaetal.， 2015； 王文静等， 2015)。高频热压成型的竹集成材在宽度方向两边各锯削30 mm，再锯削加工成2个450 mm(长)×50 mm(宽)×20 mm(高)的试件，按GB/T 17657—2013在CMT-4204万能力学试验机上进行抗弯曲和抗剪切试验，测量抗弯强度和剪切强度。每组试验重复3次，求平均值。

图2 GJ-15-6B-I型射高频发生器(a)和GJB-PI-51B-JY型高频液压机(b)

表2 热压参数及水平

1.3 研究方法

本研究参数变量4个，各参数水平变量4个，正常试验768次(每组试验重复3次)。为了减少试验次数并保证足够的信息，采用正交试验设计，选取5列16行的L16正交表。L16正交阵列设计试验只需48次(每组试验重复3次)，如表3所示。

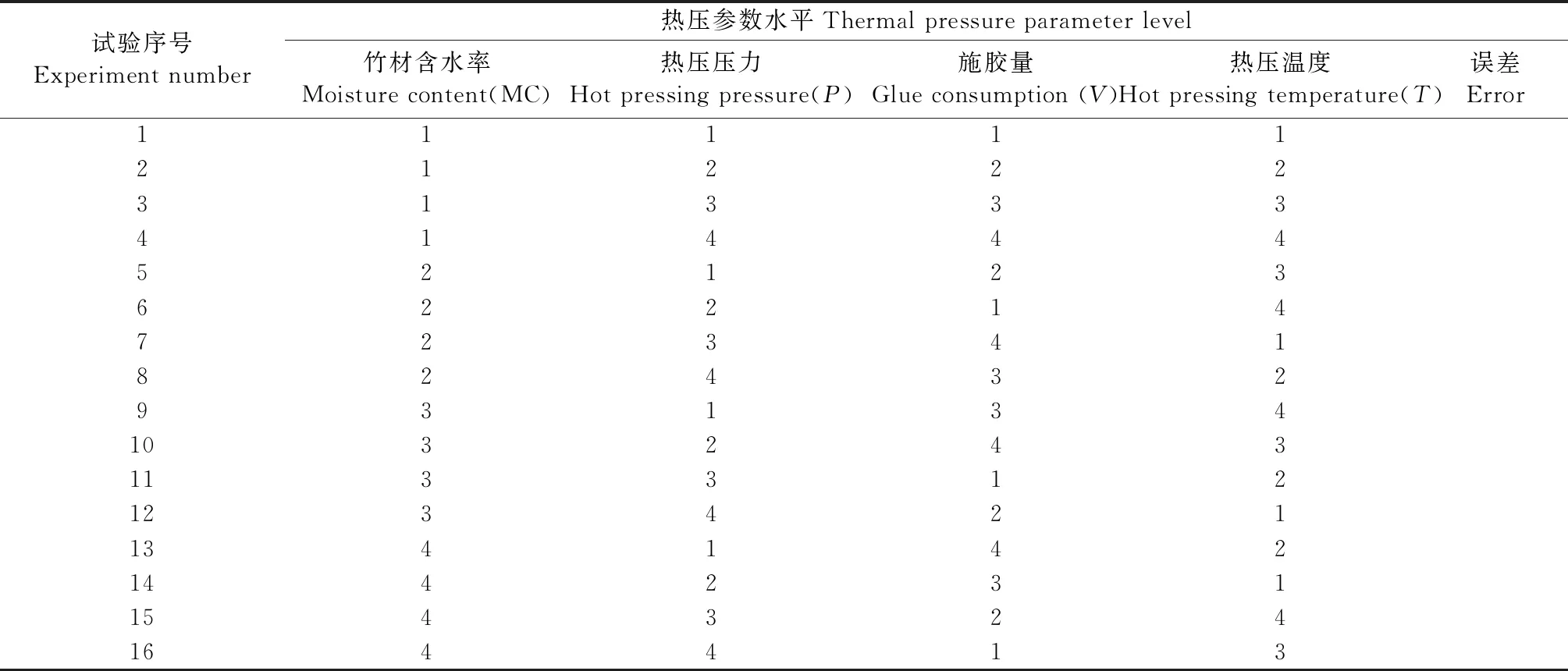
表3 L16正交试验

2 结果与分析

竹集成材高频热压正交试验结果如表4所示，对试验结果分别进行极差分析、主效应分析、交互分析、方差分析和数学建模(张浩等， 2015； Xiaoetal.， 2017)。

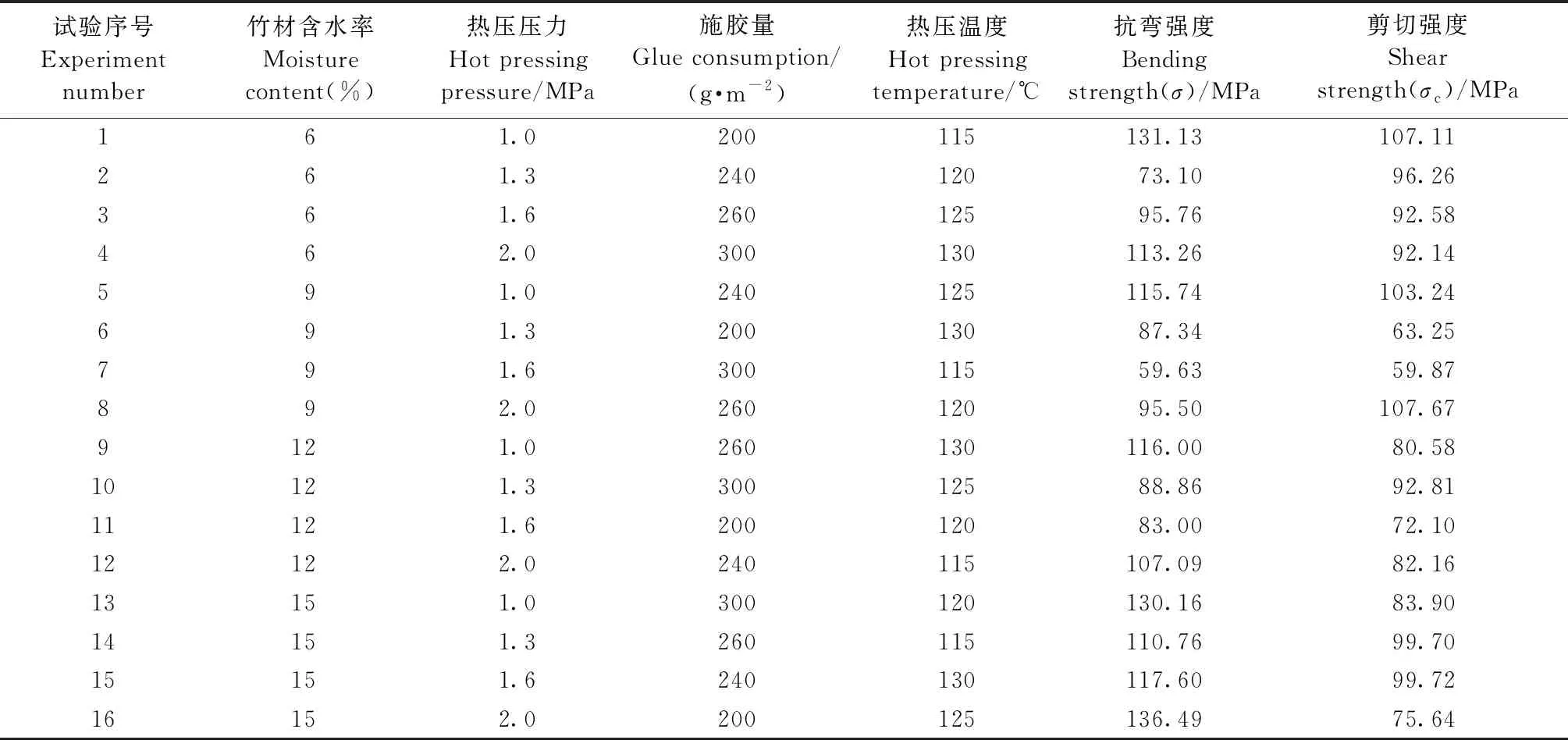
表4 正交试验结果

2.1 极差分析

由于试验设计是正交的，因此可在不同水平上分离出每个参数对竹集成材力学性能的影响。平均抗弯强度和平均剪切强度的极差分析表如表5所示，此外还计算了16次试验的总平均抗弯强度和剪切强度。可见，热压压力和竹材含水率对平均抗弯强度影响特别显著，热压温度对平均抗弯强度影响次之，最后是施胶量； 施胶量对平均剪切强度影响特别显著，竹材含水率对平均剪切强度影响次之，热压压力是第3个最显著的因素，最后是热压温度。平均抗弯强度为103.839 MPa，平均剪切强度为88.046 MPa。

2.2 主效应分析

抗弯强度和剪切强度主效应分析结果如图3所示。竹材含水率对抗弯强度和剪切强度影响较大，竹材介质损耗因素小于酚醛树脂，酚醛树脂介质损耗因素远小于水(陈勇平等， 2007)。在高频介质加热时，竹材含水率过高会优先吸收大量热量蒸发水分，影响酚醛树脂固化，继而影响竹集成材的力学性能。

当竹材含水率从6%增至9%时，抗弯强度趋于下降显示最低抗弯强度，剪切强度大幅下降，竹材含水率6%显示最高剪切强度； 当竹材含水率从9%增至12%时，抗弯强度响应值增大，剪切强度响应值继续下降显示最低剪切强度； 当竹材含水率从12%增至15%时，抗弯强度继续增大得最佳抗弯强度，剪切强度逐渐上升但小于最大剪切强度。

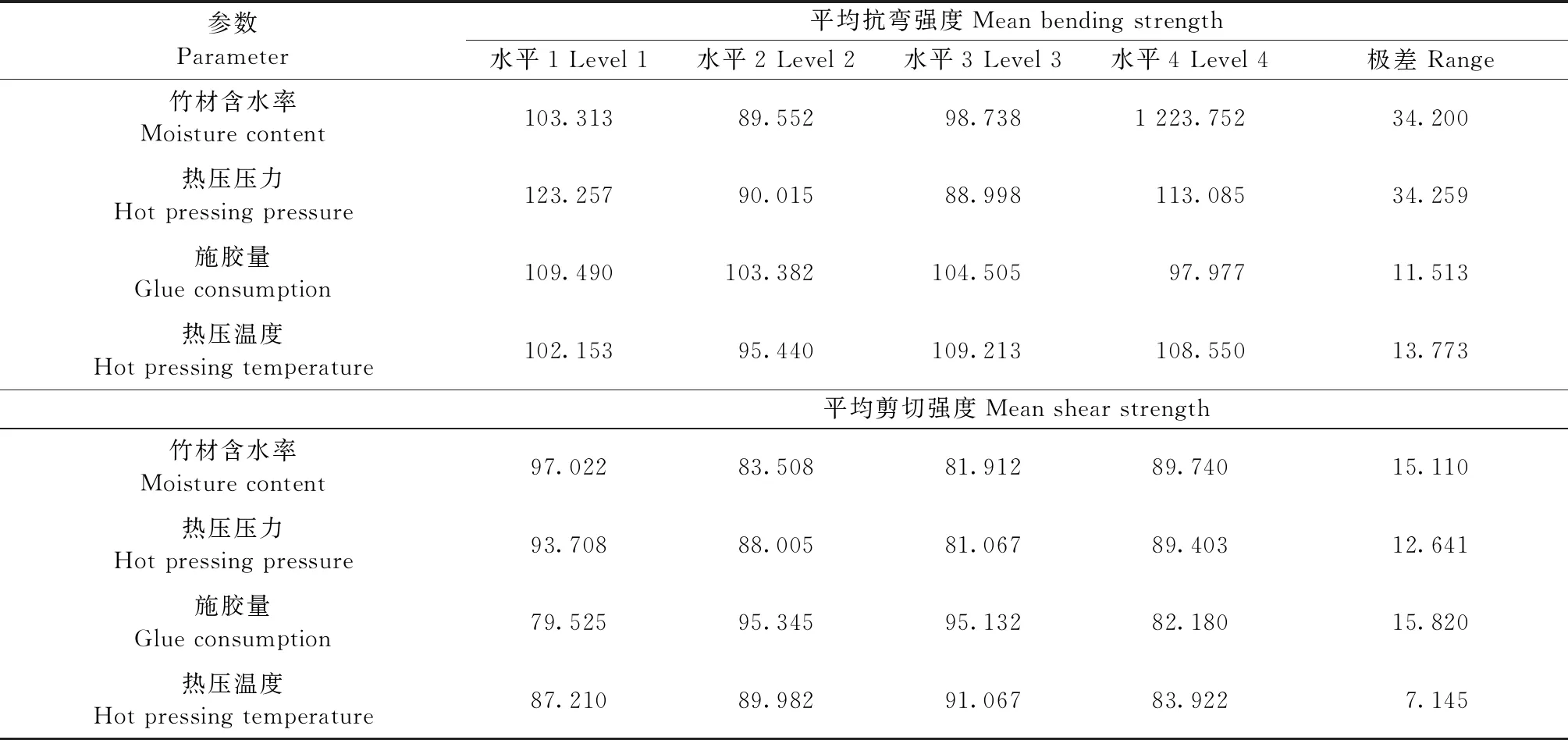
表5 极差分析

当热压压力从1 MPa增至2 MPa时，抗弯强度和剪切强度均呈先下降后上升趋势，热压压力1 MPa时显示最高抗弯强度和剪切强度； 当热压压力从1 MPa增至1.3 MPa时，抗弯强度大幅下降，剪切强度略微下降； 当热压压力从1.3 MPa增至1.6 MPa时，抗弯强度略微下降，剪切强度大幅下降得最低抗弯强度和剪切强度； 当热压压力大于1.6 MPa时，抗弯强度和剪切强度不断增大，但热压压力2 MPa时抗弯强度小于最大抗弯强度。

当施胶量从200 g·m-2增至300 g·m-2时，抗弯强度呈整体下降趋势， 200 g·m-2施胶量显示最高抗弯强度； 当施胶量从200 g·m-2增至240 g·m-2时，剪切强度大幅上升，并在施胶量240 g·m-2时达到最大值； 当施胶量从240 g·m-2增至260 g·m-2时，抗弯强度略微上升，剪切强度略微下降； 当施胶量大于240 g·m-2时，抗弯强度和剪切强度均大幅下降，300 g·m-2施胶量显示最低抗弯强度。

当热压温度从115 ℃增至120 ℃时，抗弯强度趋于下降显示最低抗弯强度，剪切强度逐渐上升； 当热压温度从120 ℃增至125 ℃时，抗弯强度和剪切强度逐渐增加至最大，即最佳抗弯强度和剪切强度； 当热压温度大于125 ℃时，抗弯强度和剪切强度均大幅下降，130 ℃热压温度显示最低剪切强度。

综上分析可知， 4级竹材含水率、1级热压压力、1级施胶量和3级热压温度为最佳抗弯强度的热压参数， 1级竹材含水率、1级热压压力、2级施胶量和3级热压温度为最佳剪切强度的热压参数。

图3 主效应分析

2.3 交互分析

抗弯强度和剪切强度交互分析结果如图4、5所示，具有4个热压参数的交互作用效应显示了所有2个参数组合的单独双向交互作用效应。

图4第1行3幅图自左向右显示4个竹材含水率水平(6%、9%、12%和15%)平均抗弯强度与热压压力、施胶量、热压温度的交互作用效应，第2行2幅图自左向右显示4个热压压力水平(1.0、1.3、1.6和2.0 MPa)平均抗弯强度与施胶量、热压温度的交互作用效应，第3行1幅图显示4个施胶量水平(200、240、260和300 g·m-2)平均抗弯强度与热压温度的交互作用效应。可见，所有交互作用效应都显示非平行线，表明所有参数间均存在交互作用。剪切强度交互分析结果与抗弯强度相似，所有交互作用效应都显示非平行线，表明所有参数间均存在交互作用。

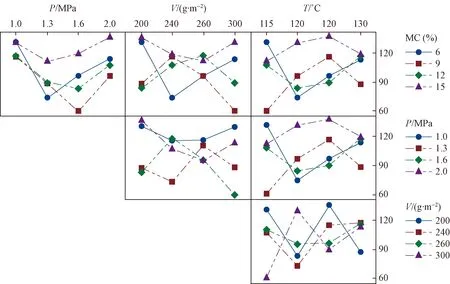
图4 抗弯强度交互分析

2.4 方差分析

抗弯强度和剪切强度方差分析结果如表6所示,通常F越大，表示参数变化对性能特性的影响越显著。

由表6可知，影响竹集成材抗弯强度的最重要因素是贡献率25.821%的热压压力，其次是贡献率18.524%的竹材含水率，施胶量和热压温度的贡献率分别为1.978%和3.677%，误差贡献率为50%。热压压力和竹材含水率显著影响竹集成材抗弯强度，施胶量和热压温度变化对抗弯强度的影响较显著。

影响竹集成材剪切强度的最重要因素是贡献率22.618%的施胶量，其次是贡献率15.221%的竹材含水率，热压压力和热压温度的贡献率分别为8.874%和3.286%，误差贡献率为50%。施胶量和竹材含水率显著影响竹集成材抗弯强度，热压压力和热压温度变化对抗弯强度的影响较显著。

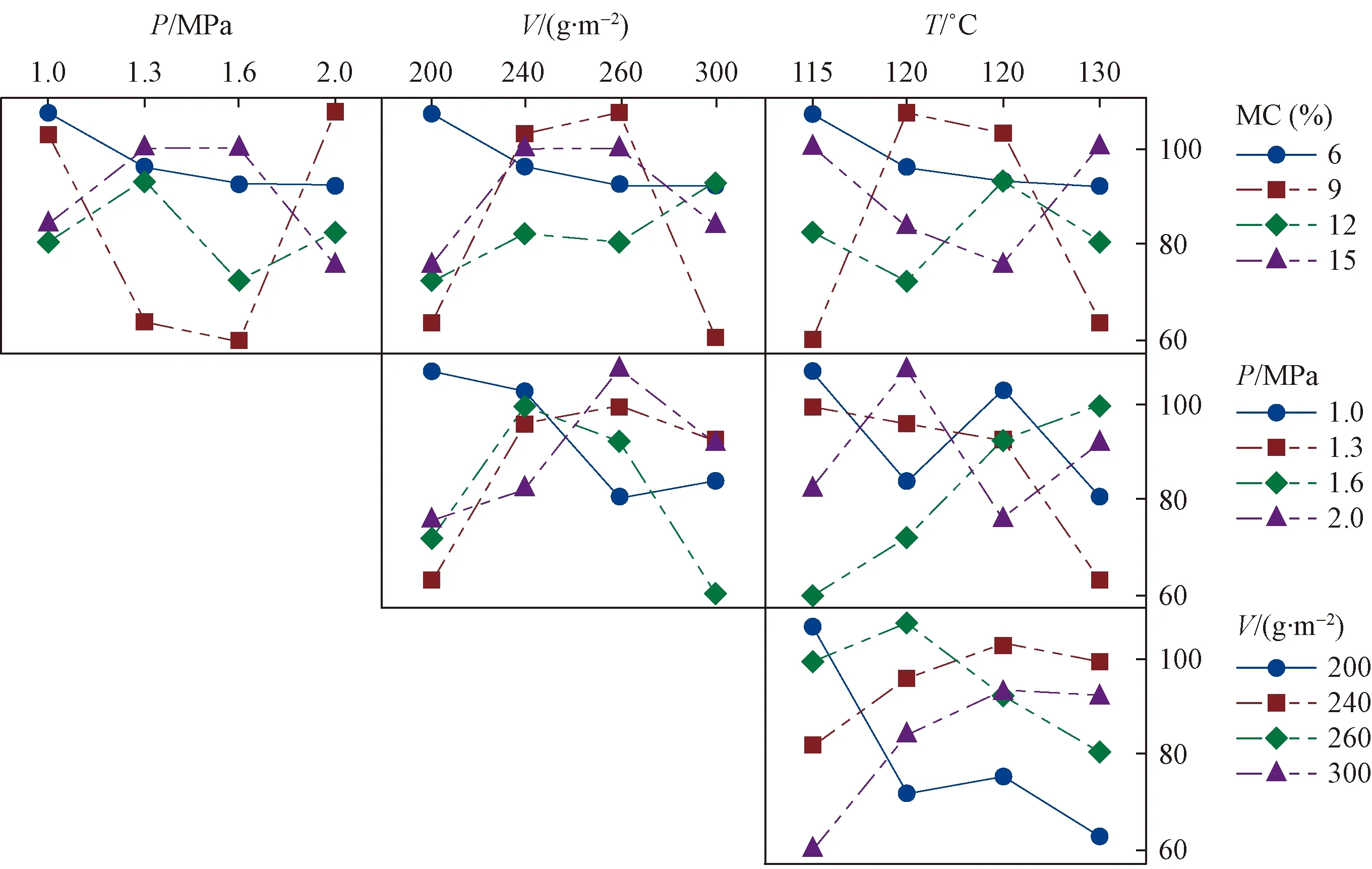
图5 剪切强度交互分析

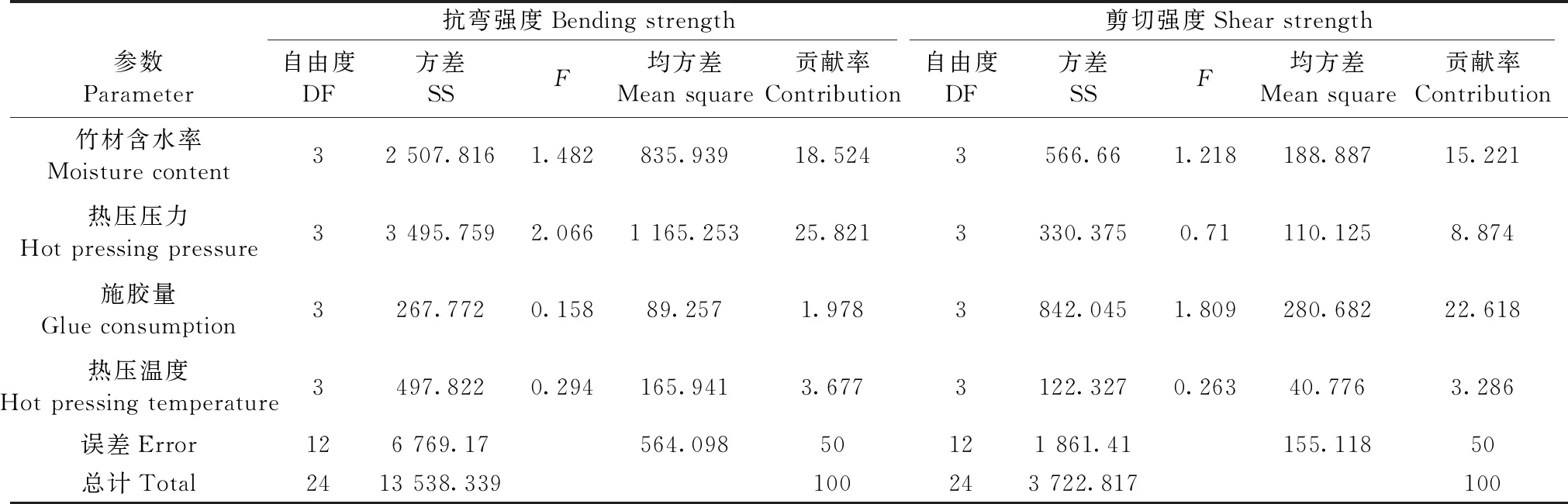
表6 抗弯强度和剪切强度方差分析

2.5 数学建模

利用SPSS 22.0软件建立数学模型(朱红兵等， 2013)，分析各热压参数对竹材集成力学性能的影响。根据试验数据建立抗弯强度和剪切强度回归方程，将一阶线性模型拟合成公式如下：

y=β0+β1x1+β2x2+β3x3+β4x4。

(1)

式中：y为竹集成材的力学性能；x1、x2、x3、x4为热压参数；β为回归系数。

一阶线性模型可表示为热压参数(竹材含水率、热压压力、施胶量和热压温度)与竹集成材力学性能的函数。根据式(1)，用于预测竹集成材力学性能与热压参数间的关系表示为：

y=β0+β1MC+β2P+β3V+β4T。

(2)

将试验结果代入式(2)，建立抗弯强度(σ)和剪切强度(σc)与热压参数间的数学模型：

σ=36+2.35MC-7P-0.109V+0.66T；(3-1)

σc=119.1-0.78MC-5.2P+0.025V-0.176T。(3-2)

测定系数(R2)是对模型解释平均值变化量的度量，抗弯强度R2=22.02%，剪切强度R2=5.98%，表明一阶线性回归模型结果不理想，还需进一步改进。

图6所示为竹集成材抗弯强度概率，解释了近80%的抗弯强度低于120 MPa，平均抗弯强度为103.8 MPa，标准差为21.75。抗弯强度数据点大致沿着直线，P>0.05，且AD统计值较低，因此可以推断数据处于正态分布。

图7所示为竹集成材剪切强度概率，解释了近80%的抗弯强度低于100 MPa，平均剪切强度为88.05 MPa，标准差为14.84。剪切强度数据点大致沿着直线，P>0.05，且AD统计值较低，因此可以推断数据处于正态分布。

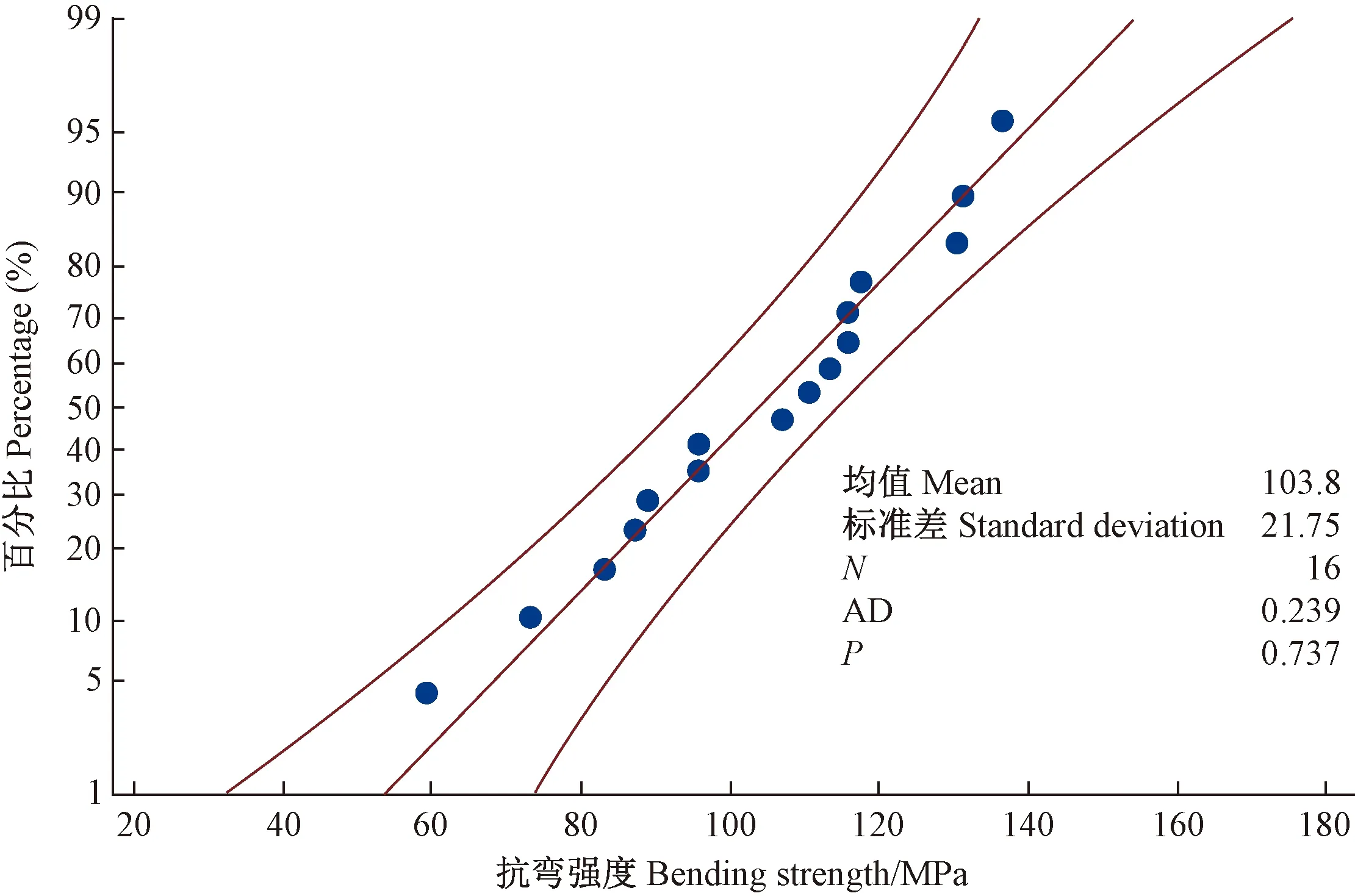
图6 抗弯强度概率

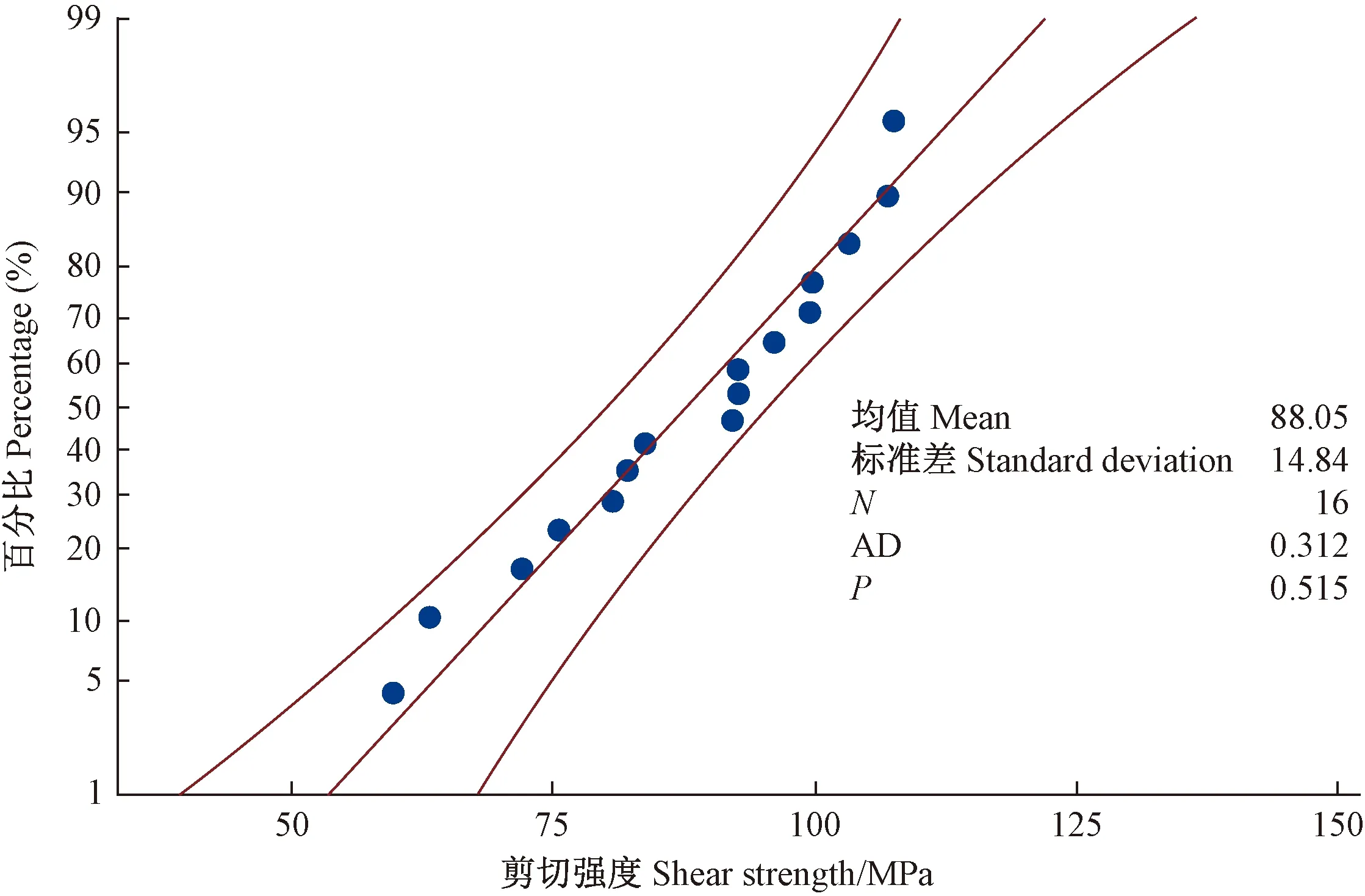
图7 剪切强度概率

抗弯强度和剪切强度数据处于正态分布，因此可用二阶模型进行拟合(张仲凤等， 2014)，表示为：

β11x1x4+β12x2x3+β13x2x4+β14x3x4。

(4)

式中：y为竹集成材的力学性能，x1、x2、x3、x4为热压参数；β为回归系数。

二阶模型可表示为热压参数(竹材含水率、热压压力、施胶量和热压温度)与竹集成材力学性能的函数。根据式(4)，用于预测竹集成材力学性能与热压参数间的关系表示为：

y=β0+β1MC+β2P+β3V+β4T+

β5MC2+β6P2+β7V2+β8T2+

β9MCP+β10MCV+β11MCT+

β12PV+β13PT+β14VT。

(5)

将试验结果代入式(5)，建立抗弯强度(σ)和剪切强度(σc)与热压参数间的数学模型：

σ=3 416.64+1.266MC-893.804P+0.44V-45.732T+0.142MC2+116.99P2-0.003 6V2+0.156T2+3.669MC·P+0.036 2MC·V-0.136MC·T-0.346PV+4.817PT+0.011 8VT；

(6-1)

σc=6 907.42+35.448MC-2 045.468P+9.553V-109.304T-2.995MC2+16.682P2-0.020 1V2+0.318T2+3.319MC·P+0.094 1MC·V-0.033MC·T-1.584PV+19.383PT+0.015 8VT。

(6-2)

由于误差列的自由度为0，故删除1个或多个交互项，并重新拟合模型。根据式(6-1)，相互作用项系数VT的绝对值等于0.011 8，远小于其他各相互作用项系数，因此删除VT项，并重新拟合抗弯强度数学模型； 根据式(6-2)，相互作用项系数VT的绝对值等于0.015 8，远小于其他相互作用项系数，因此删除VT项，并重新拟合剪切强度数学模型。

修正模型表示为：

σ=2 101.23-2.579MC-895.434P+1.283V-25.662T+0.335MC2+124.976P2-0.003 1V2+0.09T2+3.71MCP+0.034 MC·V-0.129MC·T-0.092PV+4.108PT；

(7-1)

σc=5 146.898+30.305MC-2 047.89P+10.684V-82.446T-2.736MC2+27.382P2-0.019V2+0.229T2+3.374MC·P+0.091MC·V-0.024MC·T-1.244PV+18.437PT。

(7-2)

抗弯强度修正模型R2=93.2%，剪切强度修正模型R2=97.1%，均接近于1，表明重新拟合的数学模型能够很好拟合实际数据，所得数学模型可靠。

3 讨论

竹集成材力学性能是衡量其质量的重要指标，抗弯强度和剪切强度与所建数学模型最大值对应时，可考虑为最佳结果，即最优力学性能。利用Matlab 2010软件，表7列出了基于修正模型(7-1)和(7-2)的最佳热压参数组合： 竹材含水率15%、热压压力2.0 MPa、施胶量260 g·m-2、热压温度130 ℃为抗弯强度最优解(168.51 MPa)； 竹材含水率10.2%、热压压力2.0 MPa、施胶量240 g·m-2、热压温度130 ℃为剪切强度最优解(263.26 MPa)。高频热压成型竹集成材的力学性能较优，为竹集成材高频热压成型大规模推广提供了理论依据。在后续研究中，可增加高频热压试验参数和水平，丰富试验数据，进一步深入探索竹集成材高频热压成型机制。

表7 力学性能优解

4 结论

竹材含水率、热压压力、施胶量和热压温度4个参数变量对高频热压成型竹集成材力学性能均有影响，热压压力对竹集成材抗弯强度影响较显著，施胶量对竹集成材剪切强度影响较显著。本研究在此基础上提出了一个热压参数对竹集成材抗弯强度和剪切强度影响的数学模型，并通过试验数据进行拟合验证，结果表明，该模型可有效反映热压参数与竹集成材力学性能间的关系，优化高频热压工艺生产的竹集成材，其力学性能满足相关标准和使用要求，可为竹集成材高频热压成型提供技术参考。