整体式U形渠道不同断面结构抗冻胀性研究
王玉宝, 王 亮, 程森浩, 胡战峰
(1. 西北农林科技大学 旱区农业水土工程教育部重点实验室, 陕西 杨凌 712100; 2. 西北农林科技大学 中国旱区节水农业研究院, 陕西 杨凌 712100; 3. 陕西省桃曲坡水库灌溉管理局, 陕西 铜川 727031)
在我国东北、西北和华北寒冷地区,渠道工程普遍存在着严重的冻害问题.冬季土体水分迁移冻结,体积膨胀,渠道衬砌在较大冻胀力下,发生鼓胀、开裂、隆起架空和滑塌等破坏,不仅缩短渠道使用寿命,降低防渗性能,而且影响灌区的正常运行[1].
近年来,相关学者对土体冻胀研究逐渐成熟,采用水-热-力三场耦合模型模拟土体冻胀过程[2-3];Lai等[4]和He等[5]通过冻胀试验和数值模拟,探究了粉土和亚黏土在寒冷环境下的冻胀表现;Liu等[6]通过数值模拟,指出U形渠道衬砌在冻胀作用下的变形破坏情况;高靖[7]、高凤[8]通过数值模拟分析衬砌受力的不均匀程度、渠道冻结力和冻胀力变化的离散程度,推导出渠道适宜倾角范围.上述模型仅对U形渠道进行结构计算,未针对不同土质、混凝土衬砌等因素提出定量关系,此外,缺少力学模型与数值模拟对渠道抗冻胀性的结合分析.
本文首先建立整体式U形衬砌渠道冻胀破坏力学模型,通过反算得到极限状态下倾角与切向冻结力的关系;然后运用COMSOL Multiphysics软件对不同倾角断面结构进行模拟,分析应力和冻胀量的变化规律,优化倾角取值;最后在考虑抗冻胀性和占地面积的条件下,找到适应于当地冻胀环境的U形渠道断面结构.
1 研究对象与方法
1.1 研究对象
本研究拟以D80整体式U形渠道为例展开研究,其断面形式如图1所示.
1.2 研究方法
1.2.1 力学模型
力学模型基于以下假设:冻胀力对称分布,两侧均以最不利的阴坡计算;冻土的弹性模量远小于混凝土的弹性模量,只考虑土体对衬砌板施加冻胀力并提供被动冻结约束[9].如图2所示,法向冻胀力q在直板处呈线性分布,直板与弧板相接处与基土牢固冻结,该点的法向冻结力为最大值,并在圆弧段均匀分布;切向冻结力τ沿直板线性分布,在直板与弧板相接处取得最大值,且随半圆心角α的增大呈线性递减,在渠底处为零[9].
建立平衡方程(考虑渠道自重):
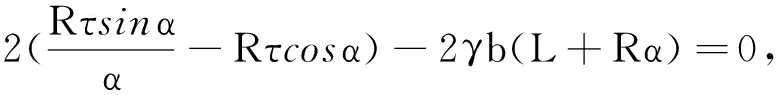
(1)
(2)
求解式(1),得冻胀力:
(3)
式中:R为弧板半径;L为直板长度;τ为切向冻结力;b为混凝土衬砌厚度;γ为混凝土容重.负温度下渠基土和渠道衬砌冻结为一个整体,衬砌和基土在冻胀作用下共同发生位移,而渠道衬砌上下部分发生位移不协调,渠基土为阻止这种位移趋势而产生了法向冻结力F,将此力简化为作用于渠顶的铰支座,支座力为F,如图2所示,则有
(4)
直板和弧板弯矩可由式(5),式(6)计算:
(5)
Mβ=-MF-Mτ+Mq-MG
(6)
直板和弧板轴力可由式(7),式(8)计算:
(7)
(8)
渠道混凝土衬砌可视为受压受弯构件,由于混凝土抗拉强度小,以极限拉应力作为破坏指标,拉应力计算式为
(9)
式中:Mmax为渠道弯矩的极大值;FN为该点轴力.当混凝土衬砌处于极限状态时,衬砌出现开裂并逐渐造成破坏.以混凝土抗拉强度为抗裂标准,计算衬砌各倾角下不同混凝土等级、厚度的极限抗冻胀倾角,计算结果见图3.
根据图3极限切向冻结力-倾角的关系进行公式拟合,提出整体式U形渠道极限切向冻结力-倾角计算公式,见式(10),确定系数范围为0.993 7~0.999 5.
tmax=m0en0θ.
(10)
式中:θ为渠道倾角;m0,n0为与混凝土性质相关的拟合系数,取值见表1.
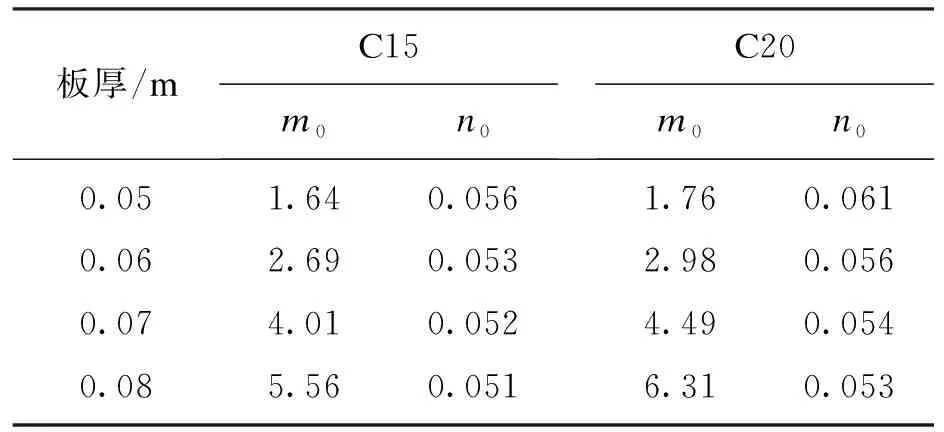
表1 极限切向冻结力公式拟合系数Table 1 Fitting coefficients of tangential limit freezing force formula
以河套灌区亚黏土和粉土为渠基土,最大切向冻结力与土壤温度密切相关,在-15 ℃以内可根据式(11)计算[9]:
τ=c+m|t|
(11)
式中:t为土壤最低温度;c,m为与土质有关的系数,取值见表2.
1.2.2 数学模型
土体冻胀过程基于以下假设:土颗粒为刚性体,在冻结过程中土颗粒不变形;土壤各向处于局部热平衡状态,即局部输出输入热流相等,温度梯度不发生变化;土质均匀,为各向同性材质.根据以上假设,建立数学耦合方程,当温度低于冻结温度时,冻结土壤的传热方程可以表示为[10]

(12)
式中:cp为质量恒压热容;λ为导热系数;L为相变潜热;T为温度.土壤中的水以液态水和冰的形式存在.在负温度下,水分迁移方程表示为
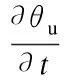
(13)
式中:θu为非饱和土壤冻结时的未冻水含量;θi为冰含量;K(θu)为土壤导湿系数,随未冻水量降低呈指数关系减小[11],亚黏土和粉土导湿系数分别由式(14)和式(15)表示.
K(θ1)=2.965 7-3θu111.259 3
,
(14)
K(θ2)=2.413 5-2θu211.586 5
(15)
冻结过程中,已冻土中部分水变成冰,其余的水仍保持未冻状态,冻土中的未冻水、冰与负温度保持动态平衡关系[11],如式(16)所示:
(16)
式中:Tref为土壤中未冻水的冻结温度;B为与土质因素有关的经验常数,取值见表2.引入Heaviside阶梯函数对土体在冻结区和未冻结区的物理参数进行表述,冻结锋面在[-d,d]区间内可以平滑过渡,表达式为
(17)
则土体导热系数和质量恒压热容分别表示为
λ=λf+(λu-λf)H(T,d)
(18)
cp=cf+(cu-cf)H(T,d)
(19)
式中:下标f和u分别表示冻结区和未冻结区.
应力场方程为[10]
Fv+σ=0
(20)

(21)
σ=σ0+C(ε-εin)
(22)
式中:v,u为位移矢量;σ为正应力;εin为温度应变;σ0为初始应力;C为弹性矩阵.
水分逐渐从未冻结区向冷端迁移,形成冰透镜体,随着体积膨胀引起土壤冻胀变形[6],则冻胀引起的应变增量可以表示为

(23)
式中,ns为土壤孔隙率.冻土强度与温度紧密相关,冻土弹性模量E和温度T之间的相关性可由经验公式[11]表示:
E=a0+b0|T|0.6
(24)
式中,a0和b0为经验系数,取值见表2.
根据实地勘测以及文献[12-13]选取河套灌区土壤参数,见表2.

表2 土壤参数Table 2 Parameters of soil
材料计算参数根据文献[6]设定,如表3所示.
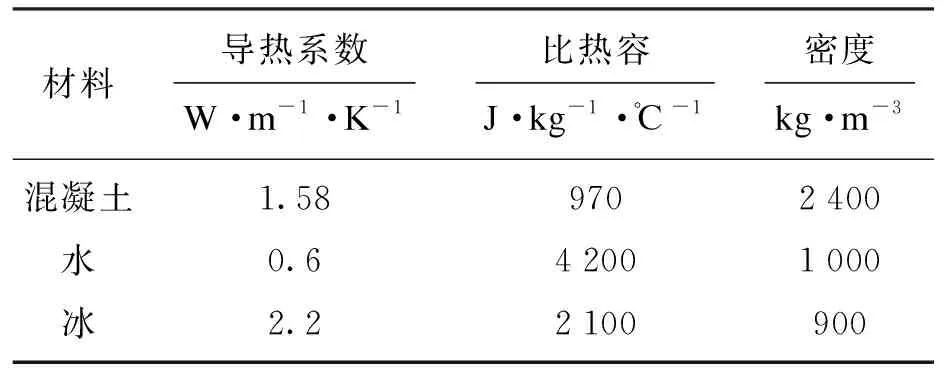
表3 材料参数Table 3 Material parameters
1.2.3 有限元模型
D80整体式U形渠道有限元网格划分如图4所示.
初始值:土体初始温度为6 ℃,含水率为0.3.左右边界指定横向位移为0,下边界指定竖向位移为0,上边界为自由边界.左右边界和下边界为绝热边界(零热梯度);上边界表面热通量为牛顿冷却定律方程[10],如式(25)所示:
n(λT)=hc(Tamb-T)
(25)
式中:hc为对流传热系数;Tamb为外界环境温度.选取河套灌区临河站2017年11月至翌年2月的气象温度作为渠道外界环境温度,如图5所示.
2 结 果
2.1 力学模型计算
取-15 ℃为土壤达到的最低温度,联立式(10)和式(11)求解得到极限状态下,整体式U形渠道的极限抗冻胀倾角,计算结果见表4.极限抗冻胀倾角与土壤冻胀性正相关;与渠道衬砌厚度和强度负相关;同一厚度下,混凝土强度增大,倾角减小,其减小程度基本不变.
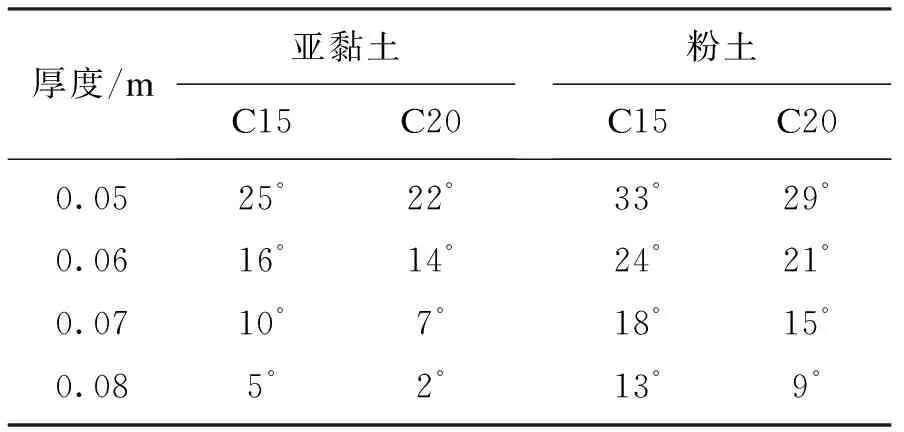
表4 极限抗冻胀倾角Table 4 Limit anti-frost heave obliquities
2.2 数值模拟
图6所示为可以看出温度在近地表土层变化大,到达一定深度后趋于稳定;渠坡冻深较大,渠底冻深较小,最大冻深位于距渠顶1.2 m处,与实际观测值一致.
图7所示为第85天亚黏土基土渠道衬砌不同倾角断面下的应力分布及形变.渠道衬砌内侧受压,外侧受拉,应力集中于渠底部;从渠底至渠顶,应力逐渐减小,倾角增大应力逐渐降低;随倾角增大,直板向渠道内侧倾斜的程度逐渐减小,而弧板上抬趋势相对明显.
如图8所示,第85天粉土冻胀量均大于亚黏土;水平冻胀量随倾角增大而减小;直板沿渠顶方向水平冻胀量增量明显.竖向冻胀量分布呈拱形,渠道衬砌呈上抬趋势,弧板上抬程度大于直板;倾角越大,竖向冻胀量越大;倾角减小,竖向冻胀量曲线趋于水平,弧板与直板各点差异逐渐减小.
如图9所示,正值表示压应力,负值表示拉应力.倾角从0°到10°,粉土、亚黏土最大拉和压应力分别减小了22.8%,26.3%和24.6%,23.6%;从10°到20°,分别减小了10.2%,9.8%,和18.1%,16.2%;从20°到30°,分别减小了8.2%,8.9%和11.4%,10.5%.表面倾角增大,最大拉、压应力值逐渐削弱,但削弱程度随着倾角的增大而减小.
3 讨 论
倾角选择适当,不仅可以依靠渠道结构削弱冻胀力,而且节约施工和维护成本.在10°~20°范围内显著削减了水平冻胀量和竖向冻胀量;同时应力削减程度相对较大,抗冻胀性提升迅速.由图10可知,相同土质下,渠道衬砌随厚度增加,抗冻胀性增量逐渐递减.10°~20°范围面积增加趋势放缓,占地面积适中,此区间内倾角断面既能节约成本,又具备一定抗冻胀能力.综上所述,整体式U形渠道亚黏土基土,选择厚度0.07 m,倾角10°;粉土基土,选择厚度0.08 m,倾角13°.
4 结 论
1) 提出整体式U形渠道极限切向冻结力-倾角计算公式,根据渠道衬砌的切向冻结力得到不同渠基土土质、混凝土衬砌强度和厚度下极限抗冻胀倾角,简化倾角求解过程,计算方便.
2) 整体式U形渠道衬砌渠底下表面最易被拉裂;倾角越小渠道越窄深,渠顶水平冻胀量越大,渠底应力越大;反之,倾角越大渠道越宽浅,渠底竖向冻胀量越大,但渠道各点相对抬升较小,渠道整体上抬,不易破坏.
3) 整体式U型渠道设计倾角在10°~20°范围内,衬砌水平和竖向冻胀量较小,抗冻胀性提升显著,占地面积适中;对于亚黏土基土,选择厚度0.07 m,10°倾角断面结构;对于粉土基土,选择厚度0.08 m,13°倾角断面结构.
致谢本文在计算、模拟及撰写过程中,得到了王正中教授、娄宗科教授、张爱军教授、何武全副教授,以及博士研究生王羿的宝贵建议和帮助,在此表示感谢.

