力电湿多物理场耦合Cell-Based光滑有限元法研究

李 明， 刘铭瑞， 周立明

(吉林大学 机械与航空航天工程学院， 吉林 长春 130025)

压电复合材料是一种应用较广的智能材料，具有应力场与电场耦合的效应[1-4].在电子设备、生物医疗及航空航天等领域都得到了广泛的应用[5-7].压电复合材料在制备及应用时常处于潮湿的环境中，材料的吸湿效应对结构的力学特性具有重要影响.研究压电材料在潮湿环境中的力学性能对压电智能结构的设计应用至关重要.

应用最广泛的有限元法(finite element method, FEM)由于其依赖单元插值的特点具有很大的局限性，如精度较低、体积锁定、对网格精度要求高等.光滑有限元法(smoothed finite element method, SFEM)是近年来被刘桂荣提出的一种新型数值计算方法，其将光滑应变技术引入到传统有限元法中.由于采用线性点插值来建立形函数，省略了计算形函数导数的过程，极大地改善了FEM的不足，使得光滑有限元在处理不规则网格时具有较高的稳定性、收敛性和精度[8].随后SFEM得到了极大的发展，一系列SFEM被提出并应用于结构分析、电磁学、传热学等领域.Zhou等[9]采用Cell-based SFEM对复合材料梁进行了静力学分析.Nguyen-Xuan等[10]利用Edge-based SFEM对二维压电结构进行了自由振动分析.Feng等[11]将Face-based SFEM用于计算复合结构的非线性导热问题.Cell-based光滑有限元(CS-FEM)处理复合材料多物理场耦合问题具有一定的优势.

从空气中吸收水分的特性被称作吸湿效应.文献[12-13]研究了在原子尺度下外部环境对压电复合材料性能的影响.近年来，压电复合材料的力学特性研究取得了众多成果.Allik等[14]应用有限元法研究了三维压电结构的动力学响应问题.Wang[15]利用FEM对压电双晶片的静态和动态性能进行了分析.Wang等[16]研究了机械及电负载下压电材料的裂纹扩展问题.Weaver等[17]研究了高湿度环境下电极材料对压电陶瓷导电率的影响.Gu等[18]研究了压电传感器对湿度变化的响应.

光滑有限元法在处理多物理场耦合问题时具有优势，且未发现有相关文献采用SFEM，研究压电材料的吸湿效应.基于此，本文提出力电湿多物理场耦合CS-FEM,研究湿度对压电材料静力学性能的影响.给出了压电复合材料的本构方程、几何方程和平衡方程；推导了力电湿耦合CS-FEM静力学控制方程；构建了一种新型压电俘能器模型，求解该结构在不同湿度条件下的静力学行为.将数值计算结果与FEM进行了对比，验证了提出的力电湿多物理场耦合Cell-based光滑有限元法的正确性.

1 压电复合结构力电湿耦合Cell-based光滑有限元模型

1.1 本构方程

压电复合材料的本构方程为

σ=Cζ-eE-λΔm,

(1)

D=eTζ+εE+PΔm.

(2)

式中：σ和D为应力和电位移矩阵；ζ和E为应变和电场强度矩阵；C，e和ε分别为弹性常数、压电系数、介电常数矩阵；λ和P表示水分膨胀系数和湿电系数矩阵；λ=Cβ，β为湿膨胀系数矩阵；m表示湿度，即单位介质中水蒸气的质量分数，Δm表示湿度变化矩阵.

几何方程为

ζ=Luu,

(3)

E=-Φ.

(4)

式中:Lu和为微分算子矩阵;Φ为电势矩阵.

平衡方程为

(5)

TD=0

(6)

机械场、电场和湿度场的本质边界条件和自然边界条件如下所示：

(7)

(8)

(9)

(10)

(11)

(12)

Γ=Γu∪ΓT=ΓΦ∪Γq=Γm∪Γv

(13)

1.2 力电湿耦合Cell-based光滑有限元法

(14)

(15)

式中：Nu和NФ为CS-FEM形函数；ne为单元总数.

光滑域内一点xk处的应变和电场强度为

(16)

(17)

(18)

(19)

(20)

式中：ΓC为光滑域ΩC的边界；nu和nΦ为积分域的外法向向量.

(21)

(22)

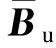
(23)

(24)

其中na为单个光滑子域的边界总数.

Cell-based光滑有限元力场、电场和湿度场耦合多物理场的控制方程为

Kuuu+KuΦΦ-KumΔm=0

(25)

KuΦTu-KΦΦΦ+KΦmΔm=0

(26)

由于湿度场与力场和电场不完全耦合，故可将湿度场以载荷的形式施加，则式(25)和式(26)可改写为

Kuuu+KuΦΦ=Fum

(27)

KuΦTu-KΦΦΦ=-FΦm

(28)

式中：Kuu，KuΦ和KΦΦ为弹性、力电耦合和介电刚度矩阵；Fum和FΦm为湿应力和湿电载荷矩阵.

(29)

(30)

(31)

(32)

(33)

式中,nc为光滑子单元的总个数.

2 数值实验

2.1 压电悬臂梁

悬臂梁由PZT-4构成，几何尺寸如图1所示，沿y轴方向极化.材料参数在表1中给出.边界条件设定为x=-15 mm处ux=0,uy=0,Φ=0，湿度变化为Δm=0.4%.结构处于平面应变状态，将CS-FEM和FEM计算的x和y方向位移及电势(广义位移)结果进行对比.

表1 PZT-4材料参数Table 1 Piezoelectric-4 material parameters

图2给出了悬臂梁上边采用两种计算方法在网格划分为30×4，60×8和120×16时的广义位移解.CS-FEM的解与传统FEM的解吻合良好，由此看出该方法的正确性和有效性；随着网格数量增加计算结果基本相同，由此验证该方法的收敛性.表2给出了不同网格下两种方法的计算时间，在采用相同网格数时两种方法的计算时间大致相同，但随着网格数的增加，CS-FEM的计算时间逐渐小于FEM，由此验证了算法的高效性.

表2 不同单元数的FEM和CS-FEM计算时间对比Table 2 Computation time of FEM and CS-FEM in different element numbers

2.2 压电俘能器吸湿效应

压电俘能器由PZT-4和钢材组成，简化模型见图3.钢的弹性模量E=2.1 GPa,泊松比υ=0.3，在x=0处ux=0，uy=0，Φ=0,网格大小为0.001 mm×0.001 mm,比较广义位移在不同的水分浓度下的变化情况.图4和图5给出了由CS-FEM和FEM计算，湿度变化为Δm=0.4%，0.5%和0.7%的俘能器AB和BC边的广义位移结果图.CS-FEM的解与FEM的解吻合良好，随着Δm的升高广义位移的相对变化也随之增大，并且在结构的自由端获得了广义位移的最大相对变化量.湿度变化Δm=0.7%时获得了结构整体的最大广义位移值.

图6给出了由CS-FEM计算的广义位移云图.从广义位移云图可见湿度的轻微变化引起了结构广义位移较大的变化，空气中湿度的变化对智能结构具有重要影响.

2.3 含孔压电俘能器吸湿效应

含孔压电俘能器由PZT-4和钢材组成，其几何尺寸、材料参数及边界条件与算例2.2相同，在PZT-4压电材料的中心开方孔(30 mm×2 mm)，其简化模型如图7所示.同样采用大小为0.001 mm×0.001 mm的网格.给出了广义位移在湿度变化Δm=0.7%下的变化情况.

图8给出了由CS-FEM和FEM计算的湿度变化为Δm=0.7%的俘能器BC边的广义位移.图9给出了由CS-FEM计算，Δm=0.7%的广义位移云图.从图8中可以得出与2.2节类似的结论.将图8与图5比较可以看出，在只受潮湿环境影响时俘能器结构的变化对广义位移几乎不产生影响.从图9中看出，采用湿度变化Δm=0.7%时获得的结构整体的最大位移及电势与2.2节不含孔的压电俘能器几乎完全一致.

3 结 论

1) CS-FEM较好地解决了压电材料受潮湿环境影响下的静力学问题.将数值模拟结果与传统FEM作对比，验证了方法的正确性与有效性.

2) 广义位移的最大相对变化量在结构的自由端附近获取.在只受潮湿环境影响时，结构变化对广义位移几乎不产生影响.

3) 湿度变化对位移和电势的影响较大，较小的湿度变化就会对广义位移产生较大的影响.