基于CP-ABE重加密的敏感数据访问控制限制方案
古丽米热·尔肯,努尔买买提·黑力力
新疆大学 数学与系统科学学院,乌鲁木齐 830046
1 引言
同一个数据拥有者发布于云上的数据之间可能存在利益冲突或由其推理出敏感信息。云上需要避免若干利益冲突数据或相互关联的数据被同一个用户访问导致的错误或敏感信息的泄露,也即对云上发布的数据,仍需要实施访问控制限制。传统访问控制限制的最为典型代表是基于角色的访问控制(Role-Based Access Control,RBAC)中的职责分离限制(Separation Of Duty,SOD)[1]和中国墙安全策略(Chinese wall security policy)[2]。
属性基加密(Attribute-Based Encryption,ABE)[3]作为一种现代加密技术广泛应用于云上批量数据的访问控制。它后续发展为密钥策略属性基加密(Key-Policy Attribute-Based Encryption,KP-ABE)和密文策略属性基加密(Ciphertext-Policy Attribute-Based Encryption,CP-ABE)[4-6]。其中CP-ABE 更适合云上数据的细粒度访问控制。CP-ABE 中为了体现用户或用户访问能力的动态变化[7]引进了用户撤销[8-10]和属性撤销[11-12]。属性撤销分为属性的直接撤销和间接撤销两种。直接属性撤销将撤销列表嵌入到密文中实现撤销操作。间接撤销通过重加密和密钥更新的方式实现属性撤销,更为灵活。Hur 等人通过使用二叉树提出了一种支持完全细粒度属性撤销的CP-ABE方案[13]。随后中国内国外的学者们提出了更有效的间接属性撤销方案,它们同样采用重加密技术和密钥更新技术[14-19]。
前期工作[20]在传统限制[1-2]的基础上分析了利益冲突数据或相互关联的数据之间的关系并定义敏感数据集(Sensitive Date Set,SDS)限制的概念,并提出了SDS限制的策略隐藏CP-ABE 方案。方案中使用SDS 监视器监控用户对数据的访问是否违反SDS限制。若是,则它销毁用户试图得到的中间密文,从而实现访问控制限制。寻找一种机制能以较小的代价对原有的CP-ABE系统进行改进,有效地隔离用户能访问的数据和不能访问的限制数据,从而实现CP-ABE的访问控制限制仍是本文的出发点。前期工作中通过改变访问树的结构实现了访问控制限制[21],本文参照文献[17]所提出的重加密与密钥更新来处理属性撤销方法,解决在文献[20]中提出的SDS 限制问题。对文献[20]中提出的SDS 限制中的每一个等价类,设定一个参数,一旦用户对某个数据的访问即将违反访问控制限制,就执行重加密和密钥更新,将该用户所拥有的相关参数失效,从而隔离用户能访问与不能访问的限制数据。这点与文献[20]比,更少的代价实现利益冲突数据或相互关联数据上的访问控制限制,使方案具有防止用户访问利益冲突数据或泄露敏感信息的能力,从而提高系统安全性。方案的分析结果表明该方案以较少的系统开销实现访问控制限制,同时能够抵抗RCCA攻击,方案安全并高效。
2 系统模型
2.1 系统框架
云存储服务器(Cloud Storage Server,CSS):云存储服务器内嵌代理服务器,是提供数据文件的存储服务和外包解密服务的实体。此外,它负责对密文重加密,它是半可信的。
密钥分发中心(Key Generation Center,KGC):它是可信赖的第三方,是用于验证数据拥有者与用户属性,并为它们生成加密公钥与解密私钥。
数据拥有者:它为数据文件制定访问策略以及限制策略,并将访问策略和限制策略嵌入数据密文后,存放于云存储服务器。
用户:它是访问云存储上加密数据的对象。每个用户都有一组属性。拥有满足访问结构的属性的用户在不违反限制的情况下能成功解密数据。
下面给出本文中使用的一些数学符号及其解释。
U={u1,u2,…,uq}:系统中所有用户的集合。
Λ={λ1,λ2,…,λt}:系统中使用的所有属性的集合。
({[M1],[M2],…,[Mn]},#k):SDS限制[20]。
[Mj],j=1,2,…,n:SDS限制中的等价类。
ξj,j=1,2,…,n:限制 SDS 中等价类 [Mj],j=1,2,…,n所对应的参数。
Su={λ1,λ2,…,λp}:用户u所拥有的属性的集合。
G:ξj→ 2U,λl→ 2U:参数ξj或者属性λl到用户组的映射。
Gξj,j=1,2,…,n:拥有第j个等价类所对应的参数ξj的所有用户的集合,限制参数用户组。
Gλl:拥有属性λl的所有用户的集合,称用户组。
Kξj(或Kλl):参数ξj(或λl)所对应的参数(或属性)组密钥。
Ti,j:SDSi限制中第j等价类所对应的2γ(单位:bit)字符串。
γ:Hash函数H1所生成的字符串长度。
2.2 算法描述
初始化:setup(κ)→(PK,MK),该阶段KGC将安全参数κ作为算法输入生成公钥PK与主私钥MK。
秘密密钥的生成:算法SecretKeyGen(MK,u,Su)→(SKu,TKu)中KGC将用户u∈U与Su作为算法输入生成令牌TKu和私钥SKu。
KEK 的生成:KEKGen(u)→(KEKs),该算法将用户集U作为输入为每个用户生成KEK。
加密算法:加密算法Encrypt(PK,M,i,j,T)→(CT)中,数据拥有者将公钥PK、消息M、访问结构T、数据M所属的SDS 限制的下标i和M所属的等价类的下标j作为输入生成密文CT。
部分解密算法:Transform(TKu,CT′)→(CT″)由代理服务器执行。它将密文CT′和用户令牌TKu作为输入,输出中间密文CT″。
解密算法:Decrypt(SKu,CT″)→(M) 用户根据中间密文CT″,用私钥SKu解密获取消息M。
2.3 安全模型
本方案的安全模型基于Replayable Chosen Ciphertext Attack(RCCA)安全,敌手A与挑战者C之间的游戏如下:
初始化:C运行setup(κ)→(PK,MK)算法保留主私钥MK,并将PK发送给A。
第一阶段:本阶段A可以向C发出一些询问,C需要给出对应的回应。在询问过程C准备空集合D和空列表L。空集合D和空列表L分别存储密钥查询和解密查询过程中的记录。
(1)密钥查询:C将属性集S作为算法输入进行SecretKeyGen(MK,PK,S)→(SKs)为A生成私钥SKs,并将属性集S存入在空集合D中,即D=D⋃S。
(2)令牌查询:C将属性集S作为算法的输入,在列表L中查询条目(S,SKs,TKs)。如果在列表L中存在条目(S,SKs,TKs),则返回TKs。反之则将S,SKs作为输入生成令牌TKs并发送给A。
(3)解密查询1:C将属性集S和密文CT作为输入执行算法Decrypt(PK,SKs,CT)→M并将M发送给A。
(4)解密查询2:C将属性集S和一对密文(CT,CT′)作为输入,在列表L中查询条目(S,SKs,TKs)。如果列表L中存在 (S,SKs,TKs) ,则执行Decryptout(PK,CT,CT′)→M并将M发送给A。反之则输出⊥。
挑战阶段:A向C发送等长的明文消息M0和M1。C随机选择其中的一个明文Mb,b∈{0,1} 在访问树T 下进行加密Encrypt(PK,Mb,T)→CT*并将CT*作为挑战密文发送给敌手A。
第二阶段:重复第一阶段,但是本阶段敌手A的询问受以下限制:
(1)对于密钥查询阶段,A不能查询满足挑战访问树T 的密钥。
(2)对于解密查询阶段,A不能查询挑战密文CT*对应的明文。
猜测:敌手输出一位b′,若b′=b则敌手赢得游戏;若b′≠b则此模型是安全的。
最后多项式时间内敌手A的优势定义为ε=其中b∈{0,1} ,ε∈R+。
2.4 预备知识
2.4.1 双线性函数
G,GT为两个阶为p的循环群,g是G的生成元。双线性映射e:G×G→GT满足如下性质:
(1)双线性。对于任意g∈G和a,b∈Zp都有e(ga,gb)=e(g,g)ab。
(2)非退化性。存在g1,g2∈G使得e(g1,g2)≠1。
经过多次沟通,我和妍妍父母终于达成共识:一定要通过医生之口清楚地告诉妍妍“你很健康”这个事实,帮助她排除心理障碍,然后再通过其他辅助手段让她逐渐接受上学,能够较好地适应学校生活,重新树立自信。
(3)可计算性。对于任意的u,υ,存在一个有效的算法计算e(u,υ)。
2.4.2 访问结构
设{P1,P2,…,Pn} 是由n个参与者组成的实体集,集合,如对于 ∀B,C,B∈A,B⊆C,有C∈A,那么A是单调的。如果集合A是{P1,P2,…,Pn}的非空子集,即,那么A是一个访问结构,包含在A中的集合成为授权集,不包含在A中的集合称为非授权集。
2.4.3 复杂性假设
本文中提出的方案在双线性对决策并行BDHE 假设[14]下可证明是安全的。
2.4.4 SDS限制
发布在云存储上的数据之间存在利益冲突或相互关联,虽然数据拥有者知道此类数据发布在云上的风险,但他在信息机密性和信息共享之间难以找到折衷。为了解决数据之间的特殊关系导致的风险,文献[20]中提出SDS限制,本文先回顾其定义和相关内容。
定义1(兼容集)设SM为某个数据拥有者数据集的一个子集,定义{M1,M2,…,Mt}⊆SM为一个兼容集,如果{M1,M2,…,Mt}的任何一个子集被同一个用户访问不产生利益冲突或用户从中推理不出任何敏感信息。对 ∀M1,M2∈{M1,M2,…,Mt}称M1和M2兼容。
为了后续表述方便,本文中一个兼容集视为一个等价类。
定义3(SDS 限制)如果任何用户不允许访问来自n个等价类中k个或更多个不同等价类中的数据并且,则 称 ({[M1],[M2],…,[Mn]},#k),2 ≤k≤n为敏感数据集(Sensitive Date Set,SDS)限制。
对 于 ({[M1],[M2],…,[Mn]},#k),2 ≤k≤n,如 果M∈[Mi],M′∈[Mj],i≠j,则M和M′不兼容;如果M,M′∈[Mi],则M和M′兼容。
本文中的SDS限制遵循文献[20]中定义的规则1~3。在这里不再赘述。
3 访问控制限制的重加密实施方案
3.1 方案描述
系统中有多个数据拥有者,而每个数据拥有者可以制定多个SDS。为了简洁,本文方案仅对一个用户u访问一个数据拥有者发布的一个SDS 限制中数据的过程进行描述。用户访问多个SDS 限制中数据的情况亦类似,从而不再赘述。本方案执行过程由图1 所示,下面对图1中每一个过程进行详细介绍。
初始化:初始化算法Setup(κ)→(PK,MK)由KGC来执行。


图1 系统框架




3.2 访问控制限制的重加密实施方案
本文为了有效解决SDS限制,不改变访问结构的情况下对文献[17]进行改进,提出了访问控制限制的重加密实施方案。
方案中数据拥有者制定访问策略和SDS限制(访问控制限制)策略并对SDS中的不同的等价类中的所有数据进行加密并将加密后的数据和SDS 对应的阈值k发送给CSS。CSS不仅存放已加密的数据,根据阈值k还能判断用户是否违反SDS限制,并通过重加密防止用户违反SDS 限制。系统对每一个等价类[Mj],j=1,2,…,n设定一个限制参数ξj,j=1,2,…,n;初始化阶段每一个等价类[Mj],j=1,2,…,n所对应的限制参数组Gξj,j=1,2,…,n包含所有的用户,即Gξj={u1,u2,…,uq},j=1,2,…,n;一旦用户违反SDS 限制,失效该用户拥有的一部分限制参数;CSS对部分数据进行重加密并更新部分限制参数组Gξj,j=k,k+1,…,n和参数组密钥。此操作有效地隔离用户能访问和不能访问的限制数据,从而实现访问控制限制。具体过程如下:
(1)数据拥有者对每一个数据Mi,j对应的密文嵌入Ti,j=H1(i)||H1(j)。Ti,j由 2γbit 字符串组成,前γbit 由数据Mi,j所在的SDS 限制的下标进行Hash 运算而得;后γbit 由数据Mi,j所在的等价类的下标进行Hash运算而得。数据拥有者执行加密算法并将包含Ti,j的密文CT发给云存储服务器。这里CSS知道的仅仅是2γbit字符串和访问限制的阈值k,而2γbit 字符串通过使用Hash函数进行模糊化得到的,实现策略的部分保护。
(2)CSS收到CT后对它进行重加密。重加密的密文CT′同样包含Ti,j。
(3)用户u向CSS 发送访问请求,CSS 对代理服务器发送(Hdr,CT)的响应。
(4)代理服务器收到响应(Hdr,CT)并判断用户u是否满足访问结构,如果用户u的属性满足访问结构,则代理服务器向用户发送部分解密的密文CT″1;向CSS 发送() 。如果用户u的属性不满足访问结构,代理服务器向用户发送⊥;向CSS不发送任何信息。
(5)假设用户u进行(2)~(4)步成功获取第二个部分解密的密文CT″2,CSS将会收到若两次收到的则用户u两次解密获取的数据来自同一个SDS限制中的同一个等价类,从而CSS只保留其中之一即可;若两次收到的则用户u两次解密获取的数据不是来自同一个SDS限制中的同一个等价类,从而CSS保存。
(6)当CSS 关于用户u保存的前γbit 相同后γbit不同的Ti,j个数达到k-1 时,表示用户u已经访问来自同一个SDS 限制中的k-1 个不同的等价类中的数据。这时用户u所拥有的参数ξj,j=k,k+1,…,n失效,即其余n-(k-1)等价类所对应的Gξj,j=k,k+1,…,n中u∉Gξj,j=k,k+1,…,n;CSS对该SDS限制中的剩余n-(k-1)等价类中的数据选取s′∈Zp,K′ξ∈Zp进行重加密。这里K′ξ与之前ξ所对应的Kξ不同。

并且,对于n-(k-1) 等价类所对应的Gξj,j=k,k+1,…,n,CSS 重新选择Gξj的最小覆盖nodeG′ξj并更新头部消息:
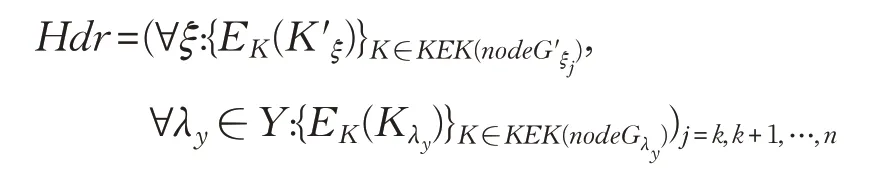
对于前k-1 不同的等价类中的数据不进行重加密操作,它们所对应的CT′与Hdr分别为:

可见,对同一个SDS 限制中前k-1 个不同的等价类中的数据而言用户u所拥有的参数ξj,j=1,2,…,k-1仍有效,即u∈Gξj,j=1,2,…,k-1,且

能够成功获取Kξ。
然而,用户u对前k-1 个不同的等价类中的数据访问结束后,u拥有的ξj,j=k,k+1,…,n失效,CSS对剩余n-(k-1)等价类中的数据进行了重加密操作,并进行了Kξ的更新;这里n-(k-1) 等价类所对应的新的Gξj,j=k,k+1,…,n不包含用户u即KEK(nodeG′ξj)⋂passKeyu=∅ ,因此u无法获取新的,从而不能解密剩余n-(k-1)等价类中的数据。
下面用简单的例子解释实现访问控制限制过程:
假设参与系统的用户有U={u1,u2,u3,u4,u5},数据拥有者制定的访问控制限制为({[M1],[M2],[M3],[M4]},#3) ,则系统初始化阶段限制参数组Gξ1=Gξ2=Gξ3=Gξ4={u1,u2,u3,u4,u5} 。表1 是用户u1,u2,u3,u4,u5的访问情况。
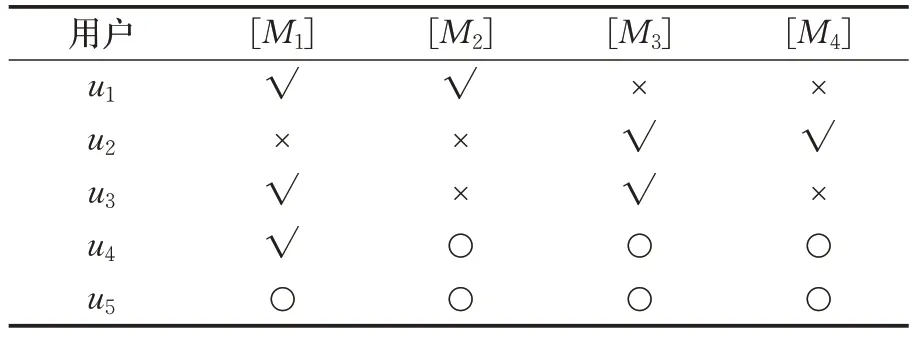
表1 用户访问情况表
4 安全性分析
定理1假设存在对手A在多项式时间内以不可忽略的优势赢得RCCA-安全模型,那么挑战者C能够以不可忽略的优势解决BDHE问题。
证明敌手A给挑战者C提供两个访问树T,T*。挑战者C获得PK=(g,e(g,g)a,h=gβ) 之后随机选取Hash函数,H1:{0,1}*→{0,1}k并将PK=(g,e(g,g)a,h=gβ)发送给敌手A。
第一阶段:敌手A提供属性集Su={λ1,λ2,…,λp}作为私钥询问的输入,由于Su不满足访问树T,T*,所以存在λi∉T,T*。由用户属性集Su不满足访问树T,T*,挑战者生成随机选取z∈Zp且令SK=z,TK=(D,∀λi∈Su:D′i,D″i)。最后,挑战者C将令牌TK发送给敌手A。
挑战:敌手A向挑战者C发送挑战消息M0、M1,挑战者随机选择其中的一个明文Mb,b∈{0,1} 在访问结构下进行加密并发送给敌手A。
第二阶段:挑战者C继续响应阶段一中的请求,如果对解密请求的响应是M0或M1,则挑战者C响应检验消息Mb,b∈{0,1}。
猜测:敌手输出一位b′,若b′=b则敌手赢得游戏;若b′≠b则此模型是安全的。
最后多项式时间内敌手的优势定义为ε=因此挑战者C以优势ε解决BDHE问题。
定理2任何不满足访问结构的用户u无法获取理想值e(g,g)r⋅s/z。
证明假设用户u的Su不满足访问树T ,则用户u从系统中无法获取有效的令牌TKu。当用户向代理服务器发送无效令牌TKu*时代理服务器向用户提供

其中,r对每一个用户而言唯一确定,防止用户合谋攻击。只有拥有有效令牌的用户才能解密CT′。而用户u的Su不满足访问树T ,所拥有的令牌也是无效的。因此该用户无法获取理想值e(g,g)r⋅s/z,理想值e(g,g)r⋅s/z是用户最后执行解密算法所用。若用户无法获取此值,该用户无法解密CT′获取消息M。
上述定理强调只有满足访问结构的用户才能够解密获取消息M,保证了CP-ABE 方案最基本的安全性要求。
定理3任何用户违反SDS限制获取有效的明文消息在计算上不可行。
证明假设用户u的属性满足访问树T ,并通过解密计算已获取来自k-1 个等价类中k-1 数据。由于用户每一次解密请求和是否能够成功解密代理服务器有目共睹,并且该用户u每一次成功获取的数据相关的(u,Ti,j)都保存在CSS 中。从而当用户u一旦获取上述的k-1 数据,该用户u拥有的限制参数ξj,j=k,k+1,…,n失效,即u∉Gξj,j=k,k+1,…,n,CSS立刻更新n-(k-1)等价类所对应的限制参数组并用新的对n-(k-1)等价类中的数据进行重加密。如果用户u想获取这n-(k-1)个等价类中数据必须获取新的K′ξ,然而用户u拥有的参数ξj失效后新的k,k+1,…,n不包含用户u即∅,因此u无法获取新的,从而不能访问其余的n-(k-1)个等价类中数据;由于系统对前k-1 数据不执行重加密,所以用户可以访问该等价类中的数据。从而任何用户违反SDS 限制获取有效的明文消息在计算上不可行。
5 效率分析
表2 将每一步算法中产生的双线性对运算eˆ,指数运算exp 作为衡量计算复杂度的主要标准,对比分析了各方案的密文、密钥长度以及计算复杂度。表中“L0”和“L1”分别表示循环群G与GT中的群元素;“—”表示方案在该算法中并没有产生双线性对和指数运算;表中“”表示方案不包含该算法。如表2所示,本方案在不增加系统的任何额外的计算开销的情况下实现访问控制限制,从而对敏感数据进行保护。

表2 计算开销的比较
对本文方案中的各算法的运行时间进行了简单的测试。系统的运行环境为Intel®CoreTMi7-4790 CPU @3.60 GHz的PC机,内存为8 GB,操作系统为Windows 10(64 bit)专业版本。软件环境为JDK12,算法依赖于Java 密码库JPBC1.2.0。测试结果如图2 所示。测试时间结果是10次测试的平均值。测试中用户最终解密的时间可以忽略不计。

图2 各算法执行所需时间
6 结束语
本文为了实现利益冲突数据或相互关联数据的访问控制限制,提出了访问控制限制的重加密实施方案。方案中,一旦用户即将违反访问控制限制,用户拥有的参数就会失效,云存储服务器对数据进行重加和密钥更新操作隔离用户可访问和不可访问的限制数据实现访问控制限制。实验分析结果表明,本方案在以较小的计算负担实现特殊数据上的限制,支持属性撤销与外包解密功能。并且,在BDHE假设下该方案能够抵抗RCCA共攻击。方案的还有一个优点是,系统启动后数据拥有者仍可以修改限制结构,即不改变门限值k的情况下已定义的限制中可以增添新的等价类,等价类中增添新的数据。

