数字空间中管路协调建模与求解

顾城歌，徐晓坤，周志宇，莫锦秋

（上海交通大学机械与动力工程学院，上海 200240）

1 引言

在一些舰船、航空飞行器、航天运载器中，作为燃料、助燃剂等物质运送通道的管路在安装时，一般是先分段制造，然后再按段拼接与对应的安装接口装配相连。但由于累积误差和焊接变形，实际安装接口会与设计值有偏差，直接按图纸生产分段管件进行拼接装配，一般都无法匹配，如果强迫装配，会使安装后管路存在预应力，降低安全可靠性。因此在这些重要场合的管路制造中会引入管路余量协调。

管路余量协调分为协调余量预留、协调量确定、协调实施三步。协调余量预留指分段制造的管件在设计时即在管件拼接处添加余量，如直管件拉长长度形成直段余量，弯管件扩大弧长形成弯段余量。协调量确定指装配前根据实际管路接口位姿确定各管件最终长度或弧长及空间拼接状态。协调实施指在管件余量段进行实际余量去除，再按协调量确定环节所得的空间拼接状态焊接。协调量确定和协调实施是在总体装配前才能得到足够信息，每次管路连接均带个性化特点。管路余量协调的传统方法是人工试配修挫法[1]。由专业技工师傅将整个管路的管件拿去安装现场与接口尝试匹配，再根据匹配情况结合个人经验进行余量修挫。多次重复上述过程直至试配的结果满足装配要求。这种传统方法严重依赖技工经验，具有很大的主观性和不确定性，在缺乏精确参数的指导下，工作量繁重且效率低下。

数字化管路协调指采用计算、分析的方法取得客观、可追溯的协调量和空间状态，不再依赖技工经验。将实物管件和接口进行数字化测量和重建，如图1所示。在数字空间进行协调量确定，将协调量结果提交输入长度、弧长及空间状态可以调整的数字化放样设备完成最后一道加工。

内容为数字空间中的协调量确定，如图1所示。即根据实际管路接口和实际已生产管件的几何特征参数信息，通过建立的管路协调模型进行协调装配状态求解，并基于遗传算法对协调状态进行优化，最后将得到的解指导后继管件协调加工。内容也可视为管路数字化装配设计，但与目前常规的管路数字化装配内涵有所不同。常规管路数字化装配设计大多处于管路设计阶段[2]，如设计空间连接管路走向、设计装配顺序、设计装配零件容差等[3-7]，而非上述所提出的针对实际已生产管件、接口的按需装配设计。

2 空间管路的协调操作问题描述

空间管路在协调安装时一般分成三段进行。可表述为“左端口-管件1-管件2-管件3-右端口”的形式，如图2所示。图中空间圆面表示的左右端口与管件1左端、管件3右端是配套的法兰连接，安装时直接相连。图中空间圆柱面表示管件的协调余量段，也即管件1、2、3在拼接处需要再设计的地方。管件其余的中间走向体部分因不参与协调，用虚拟轴线代替。协调操作时，首先将管件1左端和管件3右端与接口位姿的左右端口连接重合，经调整使三管件段在空间中走向大致正确后，再确定各管件拼接处余量的协调情况完成管件2与管件1、3的连接。对余量协调时，采用空间平面对其进行裁切，然后根据裁切剖口拼接后的径向位错大小来判定协调的好坏。一般径向位错需要小于给定的工艺参数值才能实现正常拼接。根据以上问题描述，将对协调操作中的关键特征进行抽象提取和数学表达，确定数字化空间管路协调模型的描述参数并求解，并给出目标函数对协调参数进行优化。

3 管路数字化协调模型

3.1 协调各部件的建模

在协调时，总共有法兰接口和协调余量段两类部件。法兰接口作为安装接口与管路端口的配套连接部件，可以在空间中抽象为一个特定直径的圆面。将法兰接口记作F，则其可以表示为：

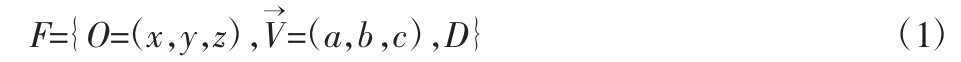
式中：O—接口圆面圆的圆心；D—圆面圆的直径；V→—圆面法向量。不加说明地，这里使用的向量均为单位化向量。

协调余量段无论直弯都可以视为由其端面沿轴线扫掠而成的扫掠件，故可以抽象用空间中的一个端面加轴线表示。端面的表达同法兰接口圆面的表达，轴线表达时直段余量表达为一个空间线段，弯段余量表达为一个空间圆弧段。

直段余量轴线空间线段可以采用线段的一端点、方向向量及长度来表达，如图3（a）所示。记直段余量为S，则其可以表示为：

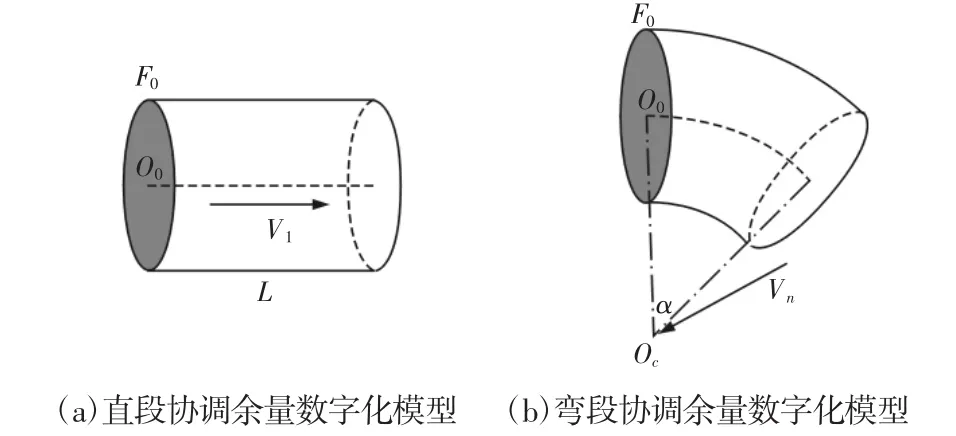
图3 管路协调余量模型Fig.3 Pipe Coordinating Segment Model

3.2 管路协调操作的建模

由于同一根管路的各分段管件具有相同的扫掠端面，在进行管路协调分析时可将各管件简化为轴线来进行分析。在管件1左与管件3右的端口法兰分别直接与左右安装接口法兰对齐连接后，仅需要确定管件2在空间中的位置。考虑所有符合要求的管路协调拼接结果，其管路轴线在空间中自始至终必定是连续不间断的。将此结论作为必要条件应用在管路协调的数字化建模中，可以得出管件2两端协调余量段的轴线必定与与其对应拼接的管件1、3余量段的轴线相交。根据上述分析结果绘制的管路协调表达，如图4所示。图4中实心线表示直段或弯段余量的轴线，虚线示意管件空间走向体，F1、F2、F3、F4表示拼接点处的各余量段端面，P、Q分别为两拼接处余量段轴线的交点。图中：粗实线—管件余量的裁切面。这里采用轴线交角的角平分面作为两管件余量段的裁切面，因为该面确立的管身裁切曲线最接近管管相交的相贯线，在理论上可以保证拼接面径向位错最小，且在实际操作上简单易行。

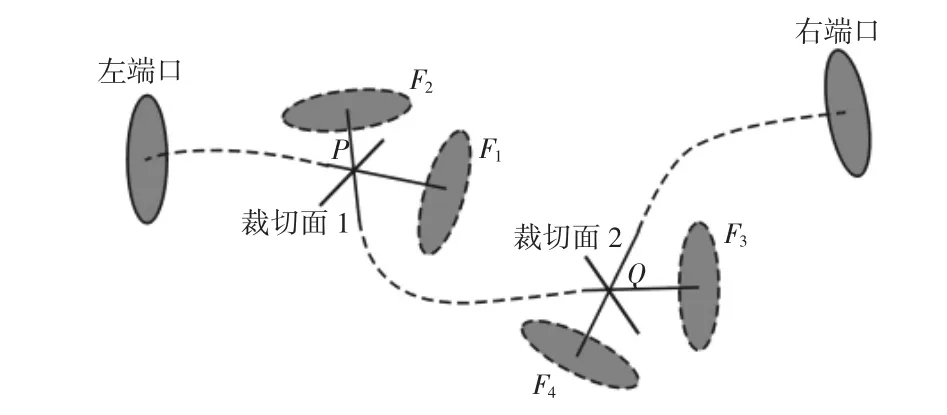
图4 管路协调抽象表达Fig.4 Abstract Expression of Pipeline Coordination

设P点在两协调余量段轴线处的位置分别为k1和k2，P点处扫掠端面分别为F1P和F2P，同理设Q点的为k3和k4以及F3Q和F4Q。则记：

3.3 协调状态的求解

通过上节所建立的管路协调模型可知，只需要在θ1，θ2，θ3，k1，k2，k3，k4，O2，→V这些协调参量中给出6个自由度的参量值便可2以通过模型求解得出管路协调的一种状态。鉴于O2，→V两参量的2取值空间过大，不便直接设定值带入模型进行求解，这里选择θ1，θ2，θ3，k1，k2，k3这六个协调参量来求解模型。相较于将这六个参数带入存在高次项的模型数学表达式中进行多元方程求解，这里给出一种更便捷的模型求解方法，如图5所示。

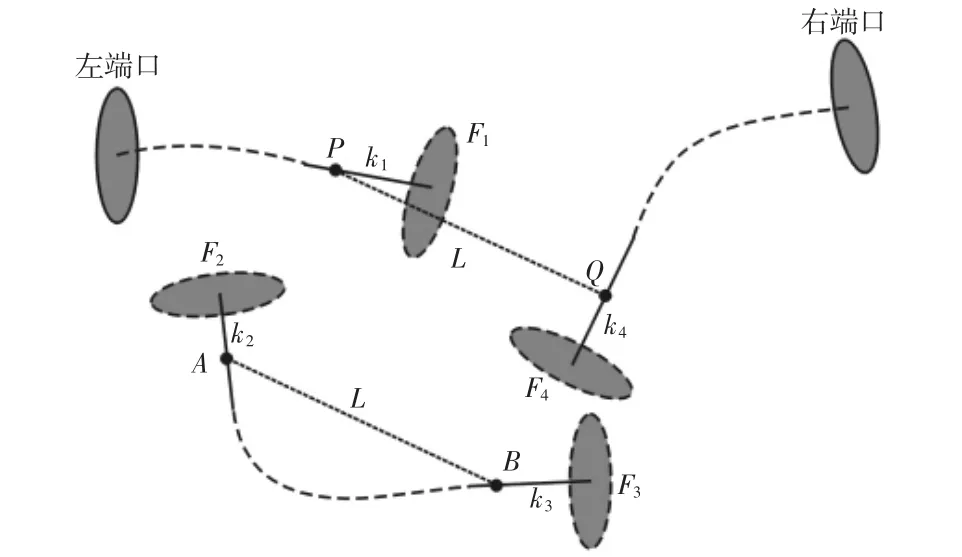
图5 模型求解方法示意图Fig.5 Model Solving Method

假设图中管件1和3的端面F1和F4的位置已经通过给出的 θ1及 θ3参量确定。P、A、B 三点是给出的 k1，k2，k3参量在各协调余量轴线上所确定的点位。设点AB之间的距离为L，若使管路能够实现协调模型中的轴线相交，则必有参量k4在协调余量轴线上确定的点Q能使PQ之间的距离也为L。至此，协调模型求解转化为只需要求解参量k4的一元方程PQ=AB。在求得参量k4后，将A、B两点分别与P、Q重合，再使管件2绕轴PQ旋转给出的θ2角度便得到了管路协调的一个协调状态。事实上，参量θ2可以通过搜寻其最符合评估指标的值来最后获得，而无需提前给定。

3.4 约束条件及评估指标

上述求得的协调状态还需要经过约束条件筛选。由于裁切面可能不垂直于管件余量段的轴线或其切线，也即存在斜切现象，故需要判断余量是否够切。这里只需判断协调余量段的外端是否够切即可，因为越过余量段内端的裁切在实际中是允许的。考虑直段余量协调裁切的情况，如图6（a）所示。图中：点划线—拼接处两余量的轴线；α—轴线的夹角；k—协调参量；D—管径。则可知管件余量段在右端端口处够切需要满足：

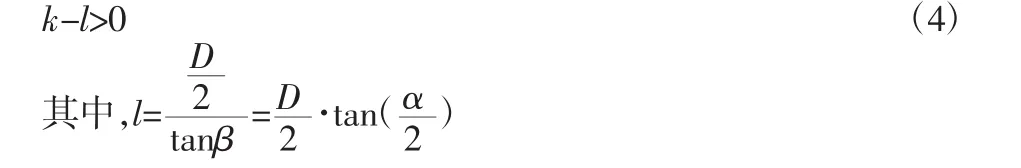
对弯段余量进行协调够切的判断时，鉴于其曲率半径一般较大，采用化曲为直的方法，将弧度参量k转化为长度参量k′，然后按照直段余量够切的式（4）进行判断。转化方法，如图6（b）所示。图中：P点—协调参量k确定的点位；R—弯段圆弧轴线的曲率半径，转化后的参量k′为从端面端点引P点处半径的垂线段长度，则可得：

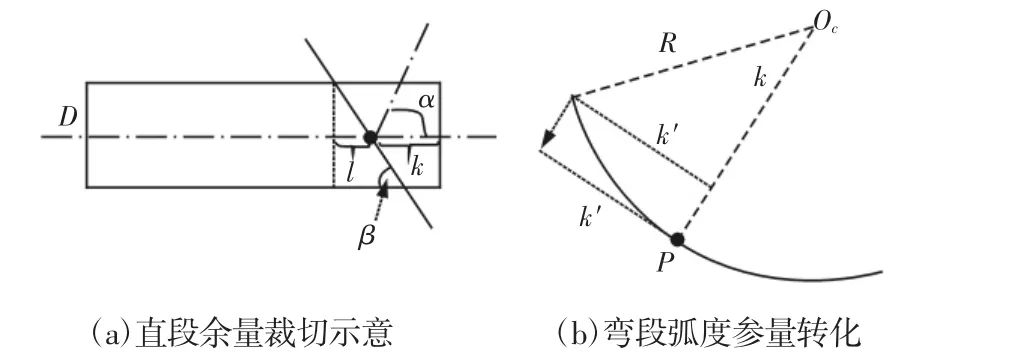
图6 管路裁切约束Fig.6 Pipe Cutting Constraints

对得到的可行协调状态建立评估指标进行优化以得到最终协调解。由上述协调模型可知，裁切面的设立已经在理论上尽可能保证了径向位错最小，现只需要保证协调后管路走向正确。将协调拼接处轴线不相切所产生的凸角作为约束管路走向的指标，记为θcvx。定义协调的凸角为：

理论设计管路轴线在空间中是处处相切过渡的，而凸角指标越小，协调后的管路在拼接处就越光顺相切过渡，也即协调管路走向越接近理论设计管路的空间轴线走向。由此建立起协调模型优化目标为min｛θcvx｝。

4 基于遗传算法的协调求解

4.1 算法描述

在不考虑协调参量θ2的情况下，文章所要处理的求解问题可以看成如下优化问题：

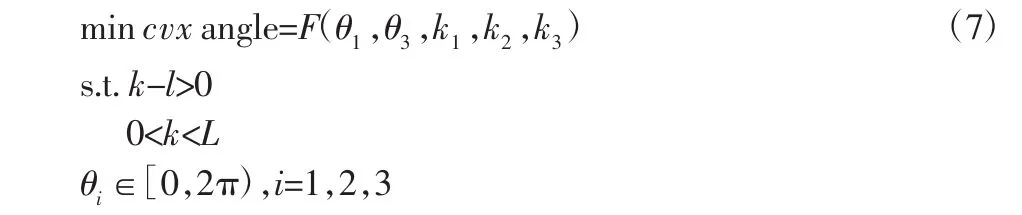
式中：F（θ1，θ3，k1，k2，k3）—将给定协调状态带入协调模型求解得出的优化目标凸角的函数关系；k-l＆gt;0—各余量够切的约束条件；L—给定的各余量长度。

鉴于优化目标函数F无法用解析方法写出，难以求取梯度信息，故这里选取启发式遗传算法对上述有约束非线性优化问题进行求解。直接采取浮点数编码，按照［θ1，θ3，k1，k2，k3］构成染色体基因。算法的终止条件设定为进化达到固定的代数。基于遗传算法所构建的流程图，如图7所示。

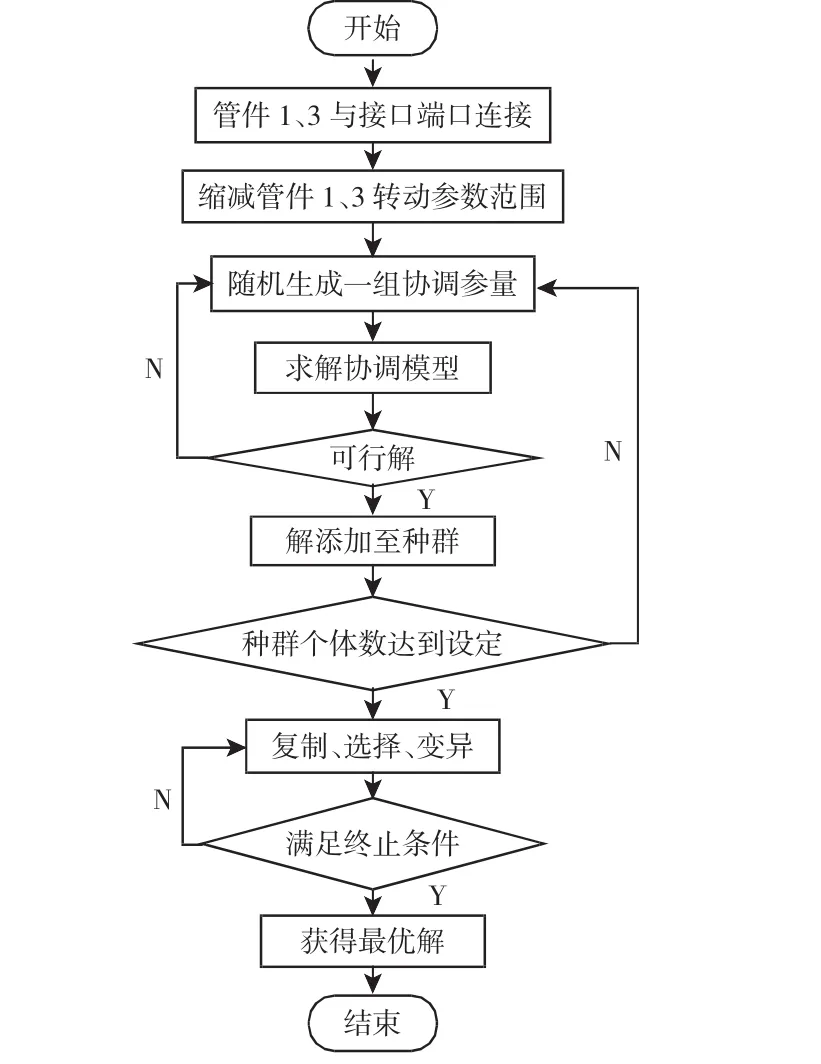
图7 算法流程图Fig.7 Algorithm Flow Chart

4.2 初始种群的产生

采用在协调参量的范围空间随机撒点的方法生成初始种群[8]。但是随机生成参量所求得的协调解可能不符合约束条件，这里采用直接舍弃不可行解重新再生成的手段处理不可行解。

考虑到管件1、3在空间中位置转动范围应在理论设计位置附近，变化不大，为提高计算速度，对协调参量中的［θ1，θ3］进行预处理缩减其范围空间。

4.3 选择、交叉与变异

根据min｛θcvx｝的优化目标确定种群中各个体的适应度，凸角越小，个体适应度越高。采用随机联赛法进行种群选择[9]。

交叉操作采用部分算术交叉策略，仅对余量协调点位置参量进行交叉操作。

变异操作采取随机单点突变法。在基因的2个控制管件1、3的转动协调参量中随机选择一个参量，在其上叠加一个扰动值完成变异操作。

经过交叉和变异所产生的后代同样要满足问题设定的约束条件，不满足的则放弃此次交叉或变异操作。

5 管路数字化协调求解实例

对提出的管路数字化协调求解方法进行实例验证。以实际中某一空间三弯管路作为示例，该管路进行安装协调时三段管件的划分及图纸设计的空间走向，如图8（a）所示。给出该管路实际协调时的一组数字化实例数据，如表1所示。

表1 一组管路协调实例的数字化数据Tab.1 The Data of One Real Pipeline Digital Coordination

设定优化种群大小为200，进化代数为100，交叉概率为0.8，交叉因子为0.1，变异概率为0.4。利用表1中数据进行协调计算，得到最终的协调后拼接结果，如图8（b）所示。图中局部放大区域黑色曲线表示的是管件余量协调裁切前的端面位置。协调拼接后的评估指标值，如表2所示。

从图8（a）、图8（b）的对比以及表2中的评估指标结果可以看出，在管路安装接口与设计值存在偏差的情况下，利用文中提出的管路数字化协调方法较好地完成了分三段装配管路的协调安装再设计。

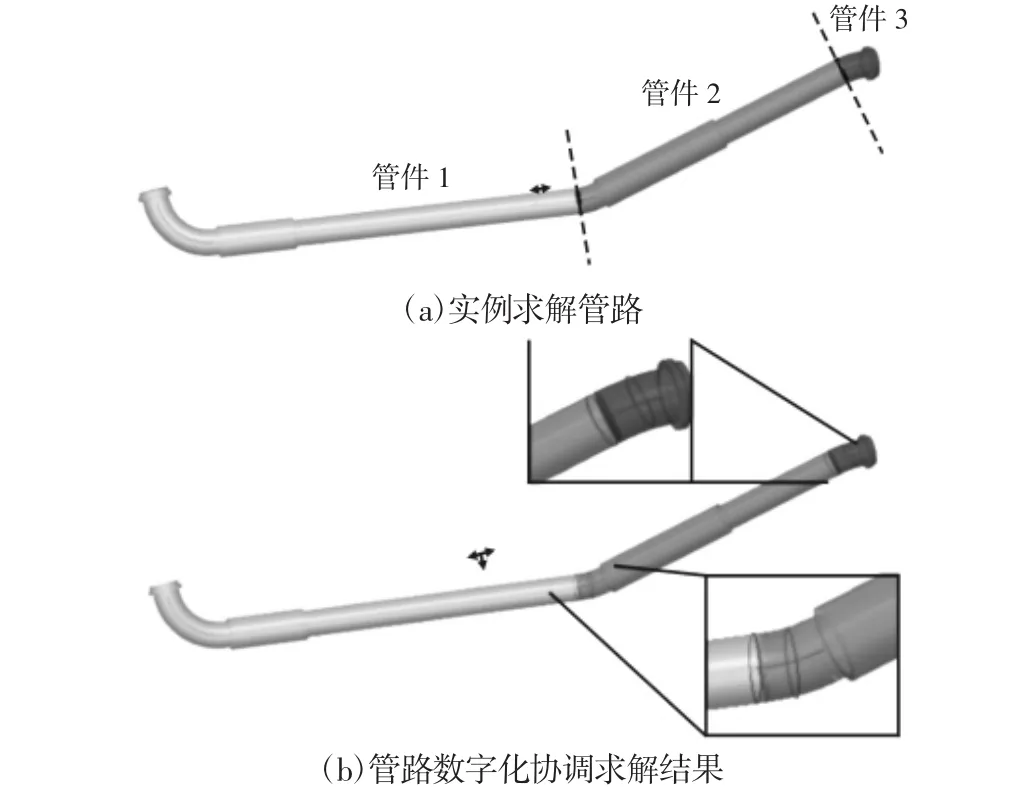
图8 管路三维显示结果Fig.8 Three-Dimension Display of Pipeline

表2 协调拼接的评估指标值Tab.2 Evaluation Results of Pipeline Coordination

6 结论

提出的数字空间中管路协调建模与求解方法，能够在管路空间安装接口与设计值存在偏差的情况下，对分三段进行安装的空间任意走向管路进行协调求解，提供参数化确定的协调指导结果。以凸角值作为协调评估目标，相较于传统人工根据多个经验目标进行协调，更加简单易操作。基于遗传算法的求解优化，计算速度快，能够大幅提高生产效率。