考虑维护且原材料易变质的单机调度问题
石 梅,石 帅,汪 晴
(1.淮北师范大学,安徽 淮北 235000;2.皖西学院,安徽 六安 237012)
机器调度问题作为一类重要的组合优化问题,被广泛应用于企业生产管理等领域。传统的机器调度问题一般假设机器在一个调度周期内一直可用,而在现实的生产作业环境下,机器往往由于需要进行定期维护及生产工具更换而造成在某段时间无法连续使用。机器故障耗费成本相对于维护成本来说更大,产生的后果也更为严重,实施维护对机器性能保证更为有利。因此,将机器因维护导致的机器不可用情形考虑到生产调度中具有重要的现实意义。
近年来,基于维护的单机调度问题引起许多学者关注,Lee 和Liman[1]对单机情形下机器具有维护时段的完工时间和问题进行分析,证明出SPT(shortest processing time,短作业优先)规则求解此问题的最坏情况误差界为2/7。针对同样的问题,Qi等[2]给出了3种启发式算法和一个分支定界算法进行求解。以上都针对作业不可中断情形,也有一些学者对作业部分可恢复的单机调度问题进行研究,目标函数为最小化最大完工时间时,LPT(longest processing time,长作业优先)算法求解此问题的最大情况误差界为α/2,其中α为需要再一次进行加工的系数[3],马英等[4]在另一篇文章中为此问题求解构造了一个启发式算法,并给出了其相对误差界。
上述研究仅考虑了机器具有不可用时段一个约束,也有学者将机器具有不可用时段和其他因素结合考虑。蒋志高和董明[5]同时考虑了机器维护和作业加工时长可变两种约束,目标函数为最小化最大完工时间。谢谢等[6]则认为对于一些加工时间较长且惩罚较小的工件存在拒绝加工情形,将机器具有周期维护和工件可拒绝结合分析,求解目标为最小化加工工件的总完工时间与拒绝工件的惩罚和。王昕等[7]同时考虑了周期维护和工时恶化两种约束,以最小化最大拖期成本和维护成本为求解目标。甘捷和曾建潮[8]对预防性维护和维修共存的情形进行分析,基于故障阀值的视情维护和役龄的混合维修策略建立了加工作业总期望完成时间最小化的集成优化模型;针对同一目标问题,甘捷[9]在视情维修的基础上增加了性能可靠性约束,为建立随机集成优化模型,推导出预防性维修概率及概率密度函数表达式,并给出了求解方法。
目前,大多数研究集中在经典调度环境,不考虑原材料、产成品会变质的情形,而现实生活中许多产品如牛奶、水果等都会随着时间推移发生变质。易变质产品对作业环境要求更高,机器故障的损失更大,也更普遍,维护保养对这类环境的机器性能保证尤为重要。因此,本文对原材料易变质性和机器存在维护时段联合约束下的单机调度问题进行分析,目标函数为作业的总变质成本最小。
1 问题描述和符号表示
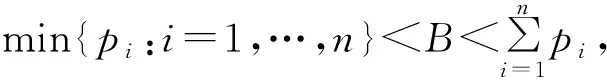
B:维护时段的开始时间;
F:维护时段的结束时间;
pj:作业Jj的加工时间,∀j∈{1,2,…,n};
λj1:作业Jj的原材料在第一阶段单位时间的变质成本,即变质率;
λj2:作业Jj的原材料在第二阶段的单位时间变质成本,即变质率;
tk:原材料变质率的分界点,即[0,tk]属于第一阶段,(tk,+∞)属于第二阶段,tk为一具体的常数,不因作业的不同而改变;
sj:作业Jj的开工时间,∀j∈{1,2,…,n};
tcj:作业Jj的变质成本;
TC:所有作业的总变质成本;

目标函数为:minTC.
2 最优解性质
通过分析该调度问题最优解的特征,根据解的性质提出相应的解决方法,思路主要是基于最优解性质设计启发式算法和对模拟退火算法进行改进。
性质1:在最优解中,对于维护时段之前的作业集和维护时段之后的作业集,其tk在之前开工的作业子集分别服从以第一阶段变质率λj1为权重的WSPT(Weighted Shortest Processing Time first)规则。
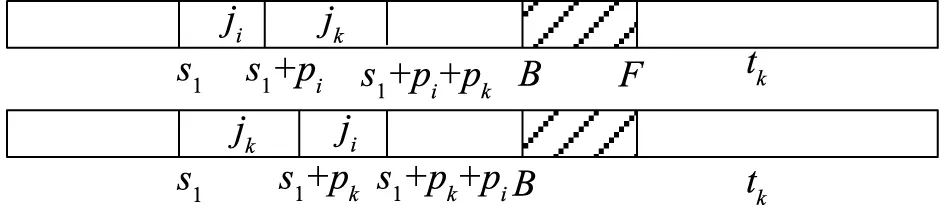
图1 性质1作业加工顺序交换示意图
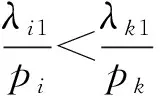
Δ=λk1*s1-λj1*(s1+pk)-λj1*s1-λk1*(s1+pi)
=λi1*pk-λk1*pi
性质2:对于维护时段之前的作业集和维护时段之后的作业集,在tk之后开工的作业分别服从以第二阶段变质率λj2为权重的WSPT规则。

图2 性质2作业加工顺序交换示意图
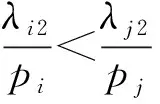
Δ=λj1*tk+λj2*(s-tk)+λi1*tk+λi2*(s+pj-tk)-λi1*tk
+λi2*(s+tk)+λj1*tk+λj2*(s+pi-tk)
=λi2*pj*λj2*pi
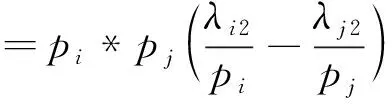
3 求解算法
为解决该问题,结合上述性质设计了启发式算法和改进的模拟退火算法,分布用H1和SA1表示,基于算法进行调度所有作业,实现作业的总变质成本最小化的目标。
3.1 启发式算法H1
Step 2:将在维护时段之前完工的作业加工时间和记为T,将F之后的作业ji重新编号,i=1,2,…,n。令初始i=1。
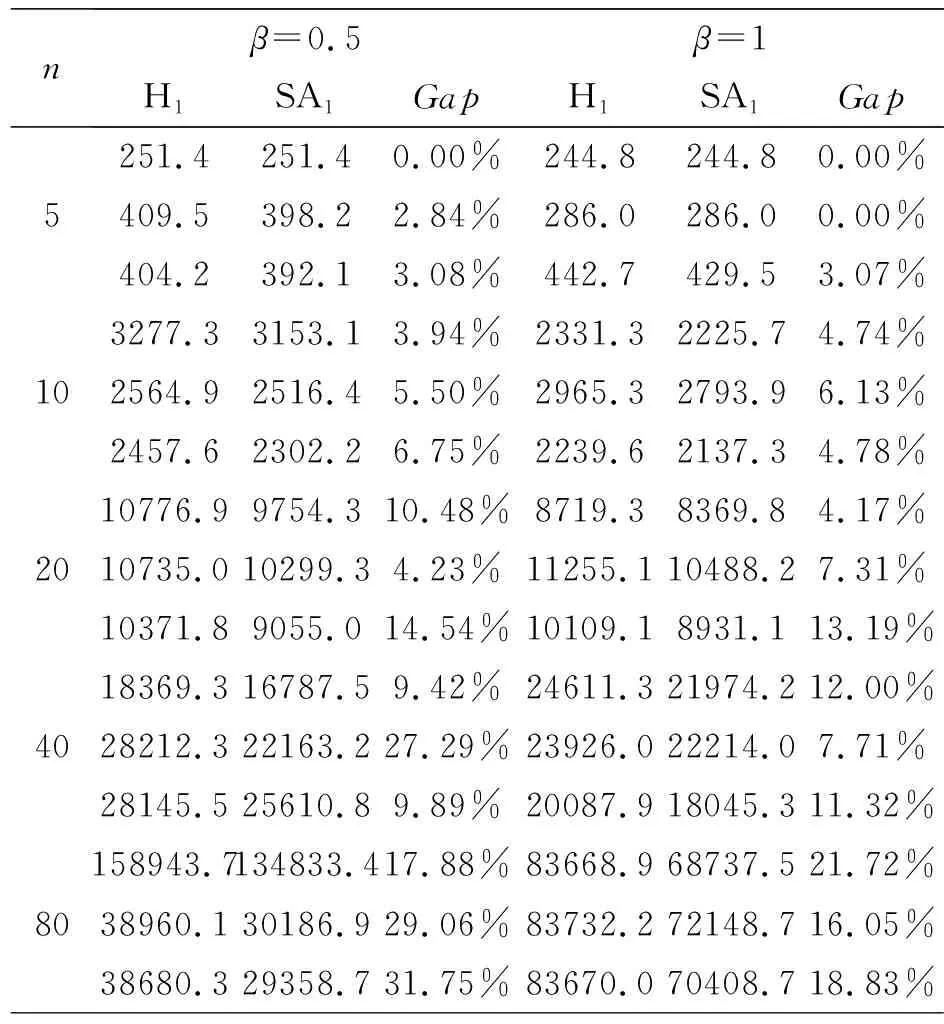
Step 3:验证T Step 4:验证ji是否满足T+pi≤B,若满足则插入,将T=T+pi转第五步,否则转第五步。 Step 5:i=i+1,若i≤n转第三步,否则转第六步。 Step 6:将维护时段之前的作业集合记为B1,将维护时段之后的作业集合记为B2,将B1中开工时间在tk之前的作业集合记为B1a,开工时间等于tk或大于tk的作业集合记为B1b,将B2中开工时间在tk之前的作业集合记为B2a,开工时间等于tk或大于tk的作业集合记为B2b。 Step 2:设置相关参数。初始温度设置为TE=1000*TC*;算法终止的温度设置为ε=0.001,降温速度θ设为0.95;同一温度下迭代次数设置为L=n2/2。 Step 3:若TE≤ε则返回当前解π,并计算其目标函数值TC(π),结束。 Step 4:在当前的调度序列中,随机选择一个作业j(允许作业j是维护时段之前的作业,当作业j为维护时段之前的作业时,相当于维护时段之前作业集内部转移),若将作业j插入到维护时段之前仍能够在维护时段之前完工,则进行将作业j插入。转第六步。 Step 5:在当前解中,在维护时段之前开工的作业中随机选择一个作业j,在维护时段之后的作业中随机选择一个作业j',若交换后j'能够在维护时段之前完工,则交换作业j和j'的所在位置然后转第六步,否则转第四步。 Step 7:ΔTC=TC(σ)-TC(π);如果ΔTC<0,则转第九步;否则转第八步。 Step 9:L=L-1;如果L=0,则TE=θ*TE转第三步,否则转第四步。 本小节给出一个算例旨在说明算法的求解过程。 例1:[B,F]=[4,6],tk=10,各个作业的基本信息如表1所示: 表1 例1作业参数 根据算法第一步:对5个作业进行初始化排序分别为:j5,j1,j4,j2,j3,依照此时排序所有的作业都将安排在不可用时段之后进行加工,根据算法第二步:F之后进行加工的作业从新编号:j1,j2,j3,j4,j5,此时在B之前加工的作业长度T为0,i=1执行算法第三步,当前T 图3 例1的调度序列 通过对表2和表3中数据的比较分析我们可以发现: (1)对于每一种作业情形下,通过SA1算法得到的目标函数值总体是优于运用启发式算法H1得到的目标函数值,从目标函数值更优的角度SA1算法性能更好。 (2)对于固定的作业数目,系数β的取值不同所得到的标函数值有所不同,优化的程度也有所不同。比较表2和表3中的计算值可以看出,作业数目相同时,β=0.5时两种算法所得到的解都更优于β=1.0时所得到的解。 (3)对于固定的系数β,对比表3和表4中的数据可以发现,随着作业数目的增加,SA1算法得到的解的目标函数值比算法的优化程度更大,也就是误差界是逐渐增大的。 (4)对比表2和表3可知,SA1算法在作业长度服从U[1,20]随机分布时比在作业分布服从U[1,100]随机分布时相对于算法的优化程度更高,具有更好的效果。 表2 作业长度服从U[1,20]随机分布的实验结果 表3 作业长度服从U[1,100]随机分布的实验结果 本文解决了在考虑预防性维护的情形下,同时考虑作业在调度时原材料具有变质特性的单机调度问题,目标函数为最小化作业的总变质成本。通过对调度问题的分析,提出了一个启发式算法H1和改进的模拟退火算法SA1。仿真结果表明,两种算法均能在合理的计算时间内求解出数据规模较大问题的满意解,同时计算结果表明改进的模拟退火算法在求解精度上总体更优于启发式算法H1,并且随着作业量的增多改进更加明显。 本文仅考虑了单机情形下具有单个维护时段情况,在今后的研究中,可有以下几种扩展方向,一方面可以保持单机情形,寻求问题的下界或分析更为复杂的维护情形;另一方面可考虑更为复杂的机器环境,如平行机、同类机等。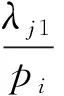
3.2 改进的模拟退火算法SA1

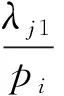
3.3 算例


4 仿真实验及分析


5 结论

