时间分数阶扩散方程的高阶Diethelm方法
杨 艳, 王希云
(1. 吕梁学院 数学系, 山西 吕梁 033000; 2. 太原科技大学 应用科学学院, 山西 太原 030024)
讨论以下时间分数阶的扩散方程
a (1) 式中:x与t分别是空间和时间变量,初边值条件如下: u(x,0)=u0(x) (2) u(a,t)=φ1(x),u(b,t)=φ2(x) (3) Diethelm[4]利用Hadamard 有限部分积分逼近Riemman-Liouville分数阶导数,用线性插值多项式逼近Hadamard有限部分积分,得到了一种有限差分格式,并证明了当u∈C2[0,T]时,截断误差为O(τ2-α)(0<α<1).方法实际上和L1方法的结果相同.Ford等[5]应用Diethelm方法求解时间分数阶偏微分方程,证明了当u∈C2[0,T]时收敛阶为O(τ2-α).Yan等[6]应用Diethelm方法,用二次插值多项式近似Hadamard有限部分积分,介绍了一种求解线性分数阶微分方程,收敛阶为O(τ3-α)(0<α<1)的数值方法,得到误差的渐近展开式,但没有进行误差估计.Li等[7]给出文献[6]中求解线性分数阶微分方程的数值方法的详细的误差估计.杨艳等[8]用类似于文献[6]的方法,得到收敛阶为3-α(1<α<2)的分数阶导数离散格式,应用于图像放大中,只有实验结果,没有稳定性的讨论. Gao等[9]直接离散分数阶导数,得到了Caputo分数阶导数的3-α(0<α<1)阶数值微分公式,并将该公式应用于求解时间分数阶扩散方程,没有误差估计.Li等[10]引入了一种3-α(0<α<1)的数值方法来近似Caputo分数导数,并在文献[11-12]中将该方法应用于求解时间分数对流扩散方程,然而其中的误差估计和稳定性分析只对0<α<1中的部分α成立.Li等[13]用Diethelm得到收敛阶为3-α(0<α<1)的分数阶导数的离散格式,用于时间分数阶的扩散方程,空间用有限元方法对于任意的0<α<1都保证稳定性. 本文提出一种基于Diethelm方法的3-α(0<α<1)阶差分格式,对区间内的所有α值都能保证该格式是稳定的. 先推导方程中Riemman-Liouville分数阶导数的离散格式,然后根据其与Caputo分数阶导数的关系,再得出Caputo分数阶导数的离散格式. 由于Riemman-Liouville分数阶导数可以写成Hadamard有限部分积分[4]: (4) 将区间[0,T]划分为n个子区间,当t=tk=kτ,(k=1,2,…,n)时,有 (5) 在区间[w0,w1],用经过三点(w0,g(w0)),(w1,g(w1))和(ws,g(ws))的二次插值多项式近似g(w),其中s为正整数,且2≤s≤k;在区间(wi-1,wi](i=2,3,…k),用经过三点(wi-2,g(wi-2)),(wi-1,g(wi-1))和(wi,g(wi))的二次插值多项式近似g(w).即,在区间[w0,w1]上, (6) 在区间(wi-1,wi]上, (7) 另一方面,由于0<α<1,w0=0是被积函数w-α-1g2(w)的奇异点,故在区间[w0,w1]上使用 0<α<1的Hadamard有限部分积分定义式(4),有 将式(6)代入上式,有 (8) 式中 (9) 同时,其他部分积分为正常积分,即 (10) 式中 (11) Qi=2i2-α-2(i-1)2-α-2(2-α)i1-α+ 2(2-α)(1-α)(i-1)1-α (12) (13) 将式(8~13)代入式(5),得 再将g(wi)=u(tk-i)代入上式整理,得以下引理. 引理1当0<α<1时,假设函数u∈C3[0,T],有以下成立,其中s≥2, (14) 当k=2时, 当k=3时, 当k≥4时, 同时注意到s≥2,上式关于s单调.当s=2时, 当s→+∞时, 2) 当i=1,2,…k,i≠s时,由式(11~13),有 记v(i)=μ(i+1)-μ(i),有v(i)>0,于是上式可整理为 记ε(i)=v(i+1)-v(i),有ε(i)>0,于是上式可整理为 3) 不妨设u(t)=1,当t=tk时, 另一方面,由于u(t)=1,有u‴(t)=0,于是 (18) 整理得 证毕. (19) uxx(xj,tk)= (20) (21) (22) 将边界和初始条件离散为 式中:j=1,2,…,m-1;k=1,2,…,n. 将差分格式(22)写成矩阵形式如下: k=1,2,…,n 式中 由引理1中式(15),及c>0有以下结论. 定理1矩阵A是严格对角占优的. 定理1显然成立,故矩阵A是可逆的,即式(22)是可解的. 即 证明用数学归纳法证明. 步骤1 证明k=1时结论成立. 当k=1时,式(22)可以整理为 j=1,2,…,m-1 (25) 将式(25)代入,可得 由引理2中式(17)取k=1,得 再由Γ(1-α)>0,将‖U1‖∞继续整理,可得 即,当k=1时,结论成立. 步骤2 假设当1 i=2,3,…,k-1 下面证明当结论对i=k成立. 与k=1时的情况相同,可得 再由式(15),得 由式(17),有以下成立, 证毕. (26) 由E0=0和定理2,可以得以下收敛性定理. O(τ3-α+h2) 考虑方程, 初边值条件如下: 该方程的精确解为u(x,t)=t3x(1-x). 表1 误差和时间的收敛阶 运算结果表明,收敛阶符合3-α.且随着α增加,s增加,而时间节点数需大于s,因此α=0.9没有举例验证. 本文应用Diethelm方法,将Riemman-Liouville分数阶导数写成Hadamard有限部分积分,将积分区间分割,每个区间用二次插值多项式逼近,得到Riemman-Liouville分数阶导数的离散格式.利用Riemman-Liouville与Caputo分数阶导数的关系,得到模型(1~3)的隐式差分格式,并证明根据α取值的不同,当s取足够大的值时,该隐式差分格式是无条件稳定和收敛的,可以保证在差分方法中,该离散格式对于任意的α都适用.进一步地,可以用更高次的多项式插值得到高阶的收敛格式,需对函数的光滑性有更高要求.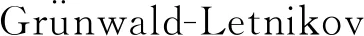

1 分数阶导数离散方法
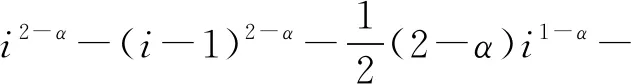
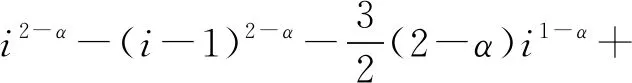
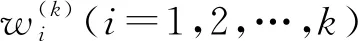
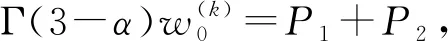
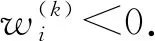

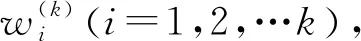

2 方程的隐式差分格式
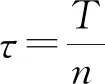
3 隐式差分格式的稳定性和收敛性
3.1 隐式差分格式解的稳定性

3.2 隐格式的收敛性
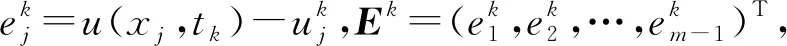

4 数值算例