完全中心Delannoy数

杨胜良, 刘 婷

(兰州理工大学 理学院, 甘肃 兰州 730050)

19世纪末Henri Delannoy引入了Delannoy矩阵.对于任意整数n和k, 矩阵D=(dn,k)满足如下递推关系:

dn+1,k+1=dn,k+1+dn,k+dn+1,k

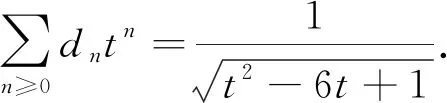
当n≥k≥0时, 令mn,0=dn,0,mn,k=dn-k,k则Delannoy三角形M=(mn,k)是一个无限下三角形也是Riordan矩阵.下面给出Riordan矩阵[4-6]的相关定理.

(1)

(2)

若Riordan矩阵G=(gn,k)=(d(t),h(t))的第0列定义为

(3)

则d(t)可以通过下面的公式得到

d(t)=

(4)

式中

2019年Barry[10]给出了完全中心系数序列的概念,定义如下.

定义1完全中心系数序列是从Riordan矩阵G=(gn,k)中第0列开始交替取对角线和它下方的一项生成,即g0,0,g1,0,g2,1,g3,1,g4,2,g5,2,….

本文主要通过利用Riordan矩阵的A-矩阵得到了几类格路计数的Riordan矩阵表达式.给出了完全中心Delannoy数的几类组合解释并证明了这些矩阵与完全中心Delannoy数之间相互联系.

1 主要结论

Delannoy三角形矩阵M=(mn,k)满足如下递推关系:

mn+1,k+1=mn,k+mn-1,k+mn,k+1n≥0,k≥1

给出它的前几行为

根据定义1得完全中心Delannoy数(en)n≥0=1,1,3,5,13,25,….通过Delannoy三角形可得完全中心Delannoy数,也可根据格路的方法得到完全中心Delannoy矩阵从而得到完全中心Delannoy数.以下给出完全中心Delannoy数的另外几个组合解释.

当允许的步子为U=(1,1),D=(1,-1),H=(2,0)和只能出现在x轴上的h=(1,0)时,从(0,0)到(n,k)限制在x轴上方的格路的个数对应的无限下三角矩阵就是完全中心Delannoy矩阵W=(wn,k),它的前几行为

它的第0列就是完全中心Delannoy数,且构造方法如图1所示.

在图1中可以发现有三种步子,则wn+1,k+1由wn,k,wn-1,k+1,wn,k+2得到.当在x轴上时,wn+1,0由wn,0,wn-1,0,wn,1得到,则有如下递推关系式:

因为wn+1,k+1=wn,k+wn-1,k+1+wn,k+2,则对应的A-矩阵为

且根据式(2)有

h(t)=t(1+h(t)2)+t2h(t)=t+th(t)2+t2h(t)

又因为wn+1,0=wn,0+wn-1,0+wn,1,可得R0(t)=1+t,R1(t)=1,Si(t)=0.根据式(4)得

则有

定理1完全中心Delannoy矩阵W为

现在考虑一个新的Riordan矩阵,在允许的步子为U=(1,1),D=(1,-1),H=(2,0)的情况下,从(0,0)到(n,k)没有限制条件的无限下三角矩阵R=(rn,k)的前几行为

可以发现在矩阵R中每一行前两列的和组成的序列就是完全中心Delannoy数(en)n≥0=1,1,3,5,13,25,且构造方法如图2所示.

在图2中可以发现有三种步子,则rn+1,k+1由rn,k,rn-1,k+1,rn,k+2得到.当在x轴上时,rn+1,0由rn,-1,rn-1,0,rn,1得到,又因为整个图关于x轴对称,所以rn,1=rn,-1,则有如下递推关系式:

因为rn+1,k+1=rn,k+rn-1,k+1+rn,k+2,根据已有结果可得

又因为rn+1,0=rn-1,0+2rn,1,可得

R0(t)=2t
R1(t)=1,Si(t)=0

根据式(4)得

则有

定理2序列{rn,k}n,k≥0的Riordan矩阵形式如下:

用得到矩阵R同样的方法将格路限制在x轴上方可得到对应的无限下三角矩阵S=(sn,k)的前几行为

可以发现在矩阵S中每一行的行和组成的序列就是完全中心Delannoy数(en)n≥0=1,1,3,5,13,25,…,且构造方法如图3所示.

在图3中可以发现也有三种步子,则sn+1,k+1由sn,k,sn-1,k+1,sn,k+2得到.当在x轴上时,因为不可到达x轴下方去,所以sn+1,0由sn-1,0,sn,1得到,则有如下递推关系式:

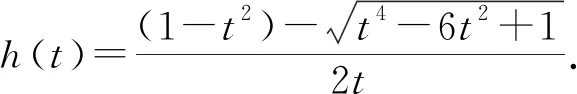
又因为sn+1,0=sn-1,0+sn,1,可得R0(t)=t,R1(t)=1,Si(t)=0.根据式(4)得

则有

定理3序列{sn,k}n,k≥0的Riordan矩阵形式如下:

2 矩阵R与S的关系

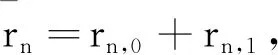
定理4对Riordan矩阵R和S,令

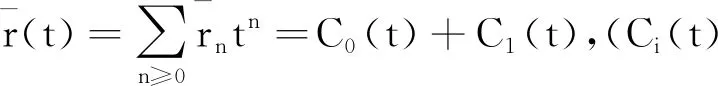
因为Ci(t)=d(t)h(t)i,所以

则

又因为