截面型式对钢桩水平受荷的影响特征

李卫超, 葛 斌, 杨 敏

(1. 同济大学 土木工程学院 地下建筑与工程系, 上海 200092; 2. 同济大学 岩土及地下工程教育部重点实验室, 上海 200092)

近年来,为充分利用材料的力学特性,可增大桩侧表面积或横截面宽度的异形截面桩在实际工程中的应用越来越广.方形灌注桩[1-2]、X形灌注桩[3]、Y形灌注桩[4]、H形钢桩[5-6]等被广泛应用于高速公路、铁路的桥梁基础和软土地基处理等实际工程中.

当前研究主要针对现浇混凝土异形截面桩的竖向承载力特性,如张敏霞等[7]采用足尺模型静载试验对比了现浇X形桩与等截面圆形桩、等周长圆形桩在竖向承载力上的差异.曹兆虎等[8]基于透明土材料和粒子图像测速技术,对等混凝土用量的X形桩和圆形桩竖向极限承载力特性进行了对比模型试验研究.针对混凝土异形截面桩基水平承载力的估算,门玉明[9]采用极限分析法推导了矩形截面桩在水平荷载下的上下限解.周航等[10]将Baguelin推导的圆形截面桩在水平荷载作用下的平面应变解推广到了现浇X形桩.

众多学者研究了混凝土桩的异形效应,但对钢桩异形效应的研究很少,尤其是水平受荷钢桩.然而相比混凝土桩,钢桩具有整体性能好、水平承载能力强、施工便捷等优势,在港口码头、跨海大桥、土体滑坡治理、近海风力发电塔等工程中得到了广泛应用[11-12].并且,从国家战略层面来看,加大钢材的使用对推进供给侧结构性改革以拉动钢材需求、消化过剩产能有着重要的经济意义.不管从重要性还是必要性角度,对水平受荷钢桩的异形效应研究都具有重要价值.

因此,本文选取钢材作为桩身材料,针对空芯圆桩、空芯方桩及X形桩,以桩身材料用量守恒为基本原则,即在长度相同的条件下,不同截面桩身用钢量相等,通过对比水平承载力和桩身最大弯矩等,初步探讨不同截面桩的水平受荷反应特征之间的差异与联系,从而为实际工程在桩基选型方面提供参考.

1 数值模型

采用有限元软件ABAQUS模拟密实砂土中水平受荷桩的反应性状.在有限元模型中,土体采用服从Mohr-Coulomb屈服准则的理想弹塑性本构模拟[13]；桩体为钢桩,采用线弹性材料模拟,土体和桩体的单元类型均采用8节点线性减缩积分单元(C3D8R),参数见表1.桩土界面之间采用摩擦接触形式,法向采用硬接触,切向采用摩尔-库伦罚函数.该模型通过已发表的现场试验实测数据标定[13-14],在标定后的模型基础上,开展了本文中的不同桩型水平受荷特性对比研究.其中,土体径向边界取20倍桩径,桩端以下土体厚度取0.5倍桩埋深 (图1),

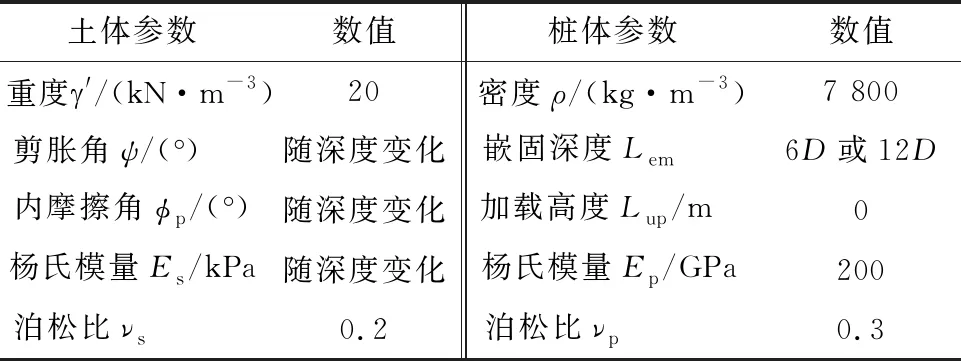
表1 有限元模型中使用的桩土参数

单元总个数从14 112到37 846不等.具体的建模过程及其余参数详见Yang等[13].

2 不同桩型设计

桩身材料守恒原则即在材料用量相等的前提下,通过改变桩身横截面型式,得到不同几何形状的桩基.设计了3种不同薄壁桩型,分别是：空芯圆桩、空芯方桩和X形桩,以下简称圆桩、方桩和X桩.基于材料守恒原则,保持不同桩身截面面积相等,且在加载方向桩基的外径D或外宽度B相等,见图 2,图中朝上箭头表示加载方向.对于截面尺寸,对实际工程中常用钢管桩的径厚比(外径与壁厚之比)进行统计,并参考美国石油协会推荐的API规范[15],将圆桩的径厚比定为87.在此基础上,确定了方桩和X桩的壁厚,据此可以计算得到圆桩截面惯性矩0.069 8 m4,方桩截面惯性矩0.093 5 m4,X桩截面惯性矩0.064 1 m4.

为研究桩长的影响特征,针对每一桩型设计了2种不同嵌固深度Lem,分别为6D和12D.所建立的有限元模型共6个.设置这2组桩长的原因是由于其桩土相对刚度有较大差异.Poulos[16]曾提出判断刚柔性桩的估算式：

(1)

式中:Ep、Es分别表示桩和土的杨氏模量;Ip表示桩的截面惯性矩.

文中地基土的杨氏模量虽然沿深度变化,但在桩埋深范围内,Es的变化幅度较小,故为了计算简便,按土层厚度取Es的加权平均值作为整个地基土的杨氏模量.若嵌固深度小于1.48R,可认为是完全刚性桩；若嵌固深度大于4.44R,则可认为是柔性桩；介于两者之间为半刚性桩.根据这一定义,将3种桩型的R计算出来,结果见表2.可见,对于本研究中长径比Lem/D为6的桩,介于刚性桩和柔性桩之间,属于半刚性桩；而对于长径比Lem/D为12的桩,均为柔性桩.

表2 按Polous法界定刚柔性桩的参数

国内依据桩的水平变形系数α判断刚柔性桩[17],α的计算见式(2),式中m表示桩侧水平抗力系数的比例系数,b0表示桩身的计算宽度.圆桩和方桩的计算宽度均有公式,本次参照方桩取X桩的计算宽度.由于缺乏实测值,因此地基土水平抗力系数的比例系数m值按照经验取：考虑到地基土为密实砂土,而单桩在泥面处水平位移较大(达到15%D,远大于规范中给出的10 mm),m值应该适当降低[17],本次取10～22的平均值.当αLem≤2.5时,认为是刚性桩；当αLem≥4时,认为是柔性桩.得到的判定结果见表 3,可见与表2一致.

(2)

3 分析与讨论

3.1 泥面处的荷载位移

3种桩型在泥面处的荷载-位移(分别记作F0和y0)曲线如图 3所示.从图3中可见,对于Lem/D=6的半刚性桩,3种桩型的水平承载力有一定差异,当泥面处变形相同时方桩和X桩的承载力略高于圆桩；对于Lem/D=12的柔性桩,在同一泥面处变形下,方桩的承载力最高,而X桩的承载力最低.

为了量化其中的水平承载力差异,以传统的圆桩为基准,衡量其余桩型与基准之间的差异,据此定义承载力偏差系数λF,计算公式如下：

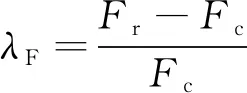
(3)

式中:Fr、Fx和Fc分别表示方桩、X桩和圆桩的桩顶荷载.根据这一定义,可以绘制出λF与泥面处变形的关系,见图4.从图4中可得：1) 对于Lem/D=6的半刚性桩,方桩承载力比圆桩高约9%,且这一偏差受变形的影响很小;X桩在变形较小(y0/D≤5%)时与圆桩非常接近,随着变形增大差异增大,变形较大(y0/D≥15%)时X桩的承载力比圆桩高约11%；2) 对于Lem/D=12的柔性桩,方桩承载力比圆桩高约15%,同样地,这一数值随泥面处变形的变化很小;X桩承载力要略低于圆桩,λF介于-5%～-2%之间,随着变形增大,两者差距在减小.

3.2 桩身变形曲线

从两个角度来分析桩身变形曲线.第一个是控制桩顶荷载F0相同,比较3种桩型的桩身变形曲线F0为圆桩在泥面处位移y0/D分别等于2.5%、5%、10%及15%四个变形阶段时的桩顶荷载,见图5a、图5b.第二个是桩身在泥面处位移y0/D同时等于2.5%、5%、10%及15%四个变形阶段时,分别比较3种桩型的桩身变形曲线,见图5c、图5d.从图5a、图5b可知,对于半刚性桩,在桩顶荷载相同的情况下,X桩和方桩的桩身变形均小于圆桩；对于柔性桩,方桩的桩身变形明显较小,X桩和圆桩基本相同,但X桩的变形略大.

对于水平受荷桩而言,水平承载力主要由两方面提供：土体水平抗力及桩身抗弯刚度.当水平土抗力、桩身抗弯刚度越大时,水平承载力越高,换言之,当水平土抗力、桩身抗弯刚度越大时,其水平方向抗变形能力越强,桩身变形会越小.实际工程中,刚性桩的水平承载力一般由前者控制,而柔性桩的水平承载力一般由后者控制.c1、r1、x1虽是半刚性桩,但表现出的桩身变形特性与刚性桩接近,即绕着土体某深度处一点发生转动,见图5a或图5c.

图5a为半刚性桩,当桩顶荷载相同时,桩身变形大小有差异,而且桩身变形的排序与截面惯性矩的排序不一致,这可能是因为所受到的土体抗力不一样.方桩和X桩的桩身变形比圆桩更小,表明在任意深度处,由单位水平变形引起的土体抗力前两者要大于第三者.这就说明,对于半刚性桩,其抗变形能力主要取决于截面形状,而与截面惯性矩的大小无必然联系；采用X桩或方桩等异形截面,其抗变形能力大于圆桩,因此桩基水平承载力得到提高.

反观柔性桩,见图5b,其桩身变形曲线排序与截面惯性矩排序一致.这可能是由于在变形零点处以下桩身变形很小,相当于嵌固作用,因此抗变形控制性因素转变为抗弯刚度.材质均为钢材,则抗弯刚度仅取决于截面惯性矩.如果截面惯性矩比圆桩小,则抗变形能力和桩基承载力也会相应比圆桩低.这一点与图 4表现出的规律一致.

从图5c、图5d可知,在泥面处位移相同的前提下,3种桩型的桩身变形基本一致.此处得到的重要结论是,在X桩或方桩等异形截面桩缺乏桩身变形计算公式的情况下,可以通过圆桩的桩身变形估算.

3.3 最大弯矩及其位置

图6为3种桩型桩身弯矩对比,分别选取归一化泥面处位移y0/D等于2.5%、5%、10%及15%四个变形阶段时的桩身弯矩.对同一桩型而言,曲线从左到右变形依次增大.

由图6可见,对于Lem/D=6的半刚性桩3种桩型的弯矩分布形状相同.在各个深度处,方桩的弯矩比圆桩略大,而X桩比圆桩略小.对于Lem/D为12的柔性桩,3者差异更加明显.为了量化弯矩之间的差异,以传统圆桩的弯矩为基准,比较方桩、X桩与基准之间的弯矩差值,定义弯矩偏差系数λyM,计算公式如下.

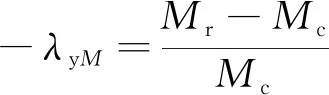
(4)

式中:Mr、Mx和Mc分别表示方桩、X桩和圆桩桩身最大弯矩值.

根据这一公式,可得λyM随变形发展的关系,见图7.

可见对于Lem/D=6的半刚性桩,变形较小(y0/D=2.5%)时Mr比Mc大10%,随着变形增大,这一数值在逐渐减小,最后稳定在5%；变形较小(y0/D=2.5%)阶段,Mx比Mc小15%,随着变形增大,这一数值迅速下降,变形达到y0/D=15%时,可认为Mx与Mc相等.对于Lem/D=12的柔性桩,最大的特点就是系数λyM对变形不敏感,方桩和X桩的系数λyM值分别稳定在15%～20%.

最大弯矩的深度见表4.可见对于半刚性桩,最大弯矩深度稳定在z=2.5D；对于柔性桩,圆桩和方桩的最大弯矩深度由浅(z=2.5D)到深(z=3.0D)发展,而X桩仍保持在z=2.5D.

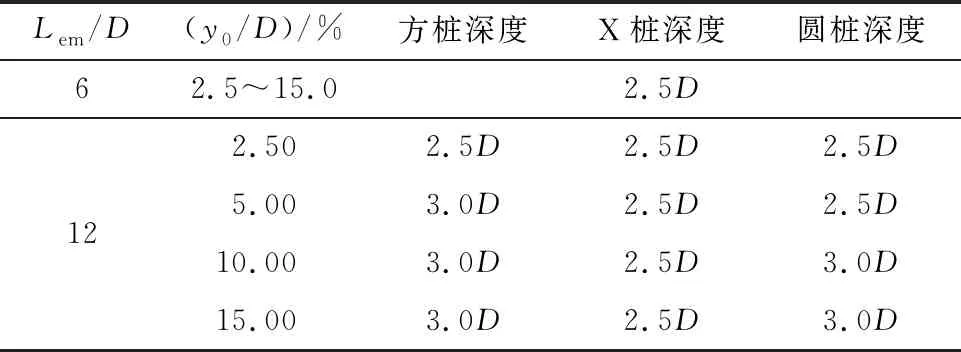
表4 最大弯矩点的深度

4 结论

通过数值模拟,研究在相同材料及用量的情况下,3种不同桩型(空芯圆桩、空芯方桩及X形桩)的水平受荷反应特性.通过对比分析,得到各桩型的桩基承载力、桩身变形与内力随变形的变化规律，及异同,从而为实际工程中桩型选择提供重要的参考依据.主要结论如下.

1) 从水平承载力特性来看,对于半刚性桩,X桩或方桩等异形截面桩基水平承载力均优于传统圆桩,其中方桩的承载力比圆桩高9%,而X桩与圆桩承载力的差异随着变形在增大,最大可达11%.对于柔性桩,方桩承载力比圆桩高15%,而X桩最小；对柔性桩而言,X桩并不能提高桩基水平承载力.

2) 半刚性桩的抗变形能力主要取决于截面形状所引起的土体抗力,而柔性桩的抗变形能力主要取决于桩身抗弯刚度.如果抗弯刚度小于圆桩,则采用异形截面无法达到提高承载力的效果.在实际工程设计中,可通过圆桩桩身变形估算X桩或方桩等异形截面桩的桩身变形.

3) 泥面处变形相同时,桩身最大弯矩从大到小依次是：方桩、圆桩、X桩.对于半刚性桩,随着桩身变形增大,3者之间的差距在减小;当泥面处变形大于15%倍桩宽时,可认为3种桩型的最大弯矩基本一致；对于柔性桩,方桩最大弯矩比圆桩高15%,X桩最大弯矩比圆桩低20%,且两者值较稳定,对变形不敏感.

4) 定义荷载偏差系数和弯矩偏差系数,在X桩或方桩等异形截面桩缺乏理论计算公式的情况下,借助这2个经验系数,可通过传统圆桩来估算桩基水平承载力、桩身变形以及桩身最大弯矩等关键指标,为实际工程设计提供了便利.