热力学模型和相平衡网络平台开发及应用

李进龙，何昌春，彭昌军，刘洪来

（1.常州大学石油化工学院，江苏常州213164；2.徐州工程学院材料与化学工程学院，江苏徐州221018；3.华东理工大学化学与分子工程学院，上海200237）

热力学模型（状态方程）和相平衡数据在流程工业的石油、化工、冶金、食品、制药等领域有着广泛的应用，是过程设计、模拟、优化及控制建模不可或缺的基础模型和数据。热力学模型的优点在于它可以适应宽广的温度和压力范围，同时描述多种不同物质（小分子、聚合物、电解质等）和相态（气态、液态、固态等）行为，避免不同相态间组分标准态的选择以及拓展计算纯流体及混合物的传递性质等[1]，而相平衡数据是模型建立的基础，可用于检验模型的适应性和实用性，同时为确定热力学模型参数提供可靠数据。

研究人员对热力学进行了长期的探索和研究，提出成千上万种各具特色的状态方程并用于实际流体相行为的描述，已可根据分子的结构和相互作用的内在机制对状态方程进行模块化设计。例如，基于这一思想并将实际物质分子假设为链状，提出了 SAFT[2]、SAFT-VR[3]、PC-SAFT[4]等模型。作者基于这一原理开发了SWCF(-VR)[5-7]状态方程，该模型已成功用于不同实际流体相行为和其他热力学性质的描述；为满足热力学理论模型和过程实际对基础数据的需求以及方便数据查询，基于互联网技术开发了流体相平衡网络平台（www.equilibria.cn）[8]，从而为流程工业的实际需求提供系统的模型和数据支撑。本文就作者自2010 年以来的上述工作做简要回顾，更多内容可参考文献[1,9—10]。

1 SWCF-VR 模型框架

借助统计缔合流体理论的建模思路，将实际物质的分子假想为链状结构，分子可呈线性、环状或具支链。若一混合体系由r元等摩尔组分（单体）Si构成，各单体可通过某种反应形成具有r个链节的链状分子：

根据统计缔合流体理论和相关函数性质，系统的状态方程可表示为：

式中，ρ0为单体链节数密度；β=1/kT，其中k为波尔兹曼常数，T为体系温度；p为系统压力；y(r)为r阶空穴相关函数；α为链节的缔合度；L为链节对距离矢量。据此，只要获得r阶空穴相关函数（通过线性近似和叠加原理计算），即可得到状态方程模型。结合方阱势能函数和考虑分子链接间的作用力机制，实际流体状态方程可表示为[11]：

式中，等号左边为系统的剩余亥氏函数；右边依次为链节单体、成链、氢键缔合、静电效应和离子缔合对体系性质的贡献。其中，V为体积；A为亥氏函数。该模型可用于不同类型流体热力学性质的描述，具体根据研究体系性质对方程右边贡献项进行取舍。例如，对非缔合流体取前两项，对缔合流体则取前三项等。对该模型的具体描述可参考文献[11]。

2 分子参数的确定

获得热力学模型中的分子参数是模型广泛应用的充分条件。在SWCF（-VR）状态方程中，用四个分子参数表征非缔合流体的分子特性，即链节数r、链节直径σ、方阱势能阱深ε和阱宽λ；对含氢键的流体（如水、醇、酸等），需借助额外的氢键缔合能和缔合分数来描述缔合贡献；若将本文模型用于电解质，需再引入离子缔合能参数。这些分子参数可以通过下述方法获得。

2.1 实验PVT 数据拟合法

通过纯流体的相平衡数据拟合确定理论模型中纯流体分子参数，是状态方程中模型参数确定的常规方法，计算中可采用如下目标函数：

式中，上标“cal”、“exp”和“S”分别表示计算值、实验值和饱和状态；Np为数据点个数。

对常规气体物质、烷烃、1-烯烃、芳香烃、卤代烃、2-酮、酯、醚等87 种非缔合化合物，拟合获得的饱和蒸气压和液体摩尔体积总体平均相对偏差（AAD）分别为1.00%和1.02%[12]；水、氨、硫化氢、醇、酚、羧酸、胺、醇胺、硫醇等78 种缔合流体对应AAD分别为 0.76% 和 0.75%[13]；44 种离子液体（假设其为缔合流体）的PVT关联表明，其密度的AAD仅为 0.06%[14]。图1（a）和（b）分别给出了水的0.01～1 000 MPa 汽液共存相图和具有不同碳链长度的咪唑阳离子与双三氟甲磺酸亚胺盐组成的离子液体的密度实验值与计算值的比较。图中，线代表理论值，点代表实验值（下同）。由图1 可以看出，两者均吻合良好，但对水临界点附近误差较大。

2.2 基团贡献法

采用基团贡献法确定模型参数的目的是赋予理论模型的预测功能，该方法将分子视为由不同基团片段构成，而相同的基团片段在不同分子中具有相同的贡献。首先，对待研究物质进行分析，根据分子结构划分基团；其次，确定由基团参数计算分子参数的方法；最后，借助实验数据拟合获得基团参数。例如，对正烷烃（除甲烷外）和1-醇化合物，只包含－CH3、－CH2－和－OH 三种基团，选择代表性物质的PVT数据拟合获得相应基团参数，进而可预测同系物中所有物质的相平衡性质。正烷烃和1-醇基团参数见表1。预测的直链碳烃（C3—C18）密度AAD为 2.06%，预测的 1-醇（C3—C18）密度AAD为1.86%，结果令人满意[15]。该方法对同系物中难以获得实验数据的体系特别有效。

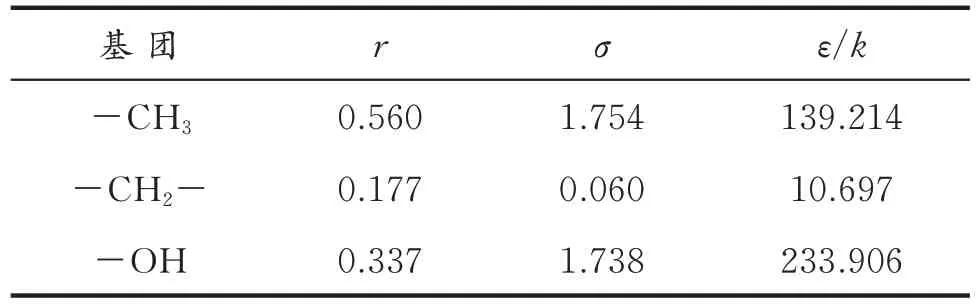
表1 正烷烃和1-醇基团参数

2.3 分子模拟的溶剂化

通过溶剂化计算，可以从理论上获得与分子结构密切相关的溶剂化自由能（ΔG）和空穴体积参数，进而结合状态方程特点并根据式（5）和式（6）确定热力学模型中的分子参数[16]。

该方法完全不依赖实验数据，只需对分子结构进行优化并进行COSMO 计算，因此相较于基团贡献法，其可有效甄别同分异构体。该方法已在立方型状态方程[17]和格子模型[18]中得到应用。将该方法与SWCF（-VR）状态方程结合，确定了烃类、卤代烃类、含氧有机物（醇、酯、醚、酮）等192 种有机化合物的模型参数，据此获得的直链烷烃、烯烃和醇类化合物的AAD分别为0.23%、0.17%和2.05%[19]。直链烯烃密度理论值和实验值比较如图2 所示。由图2 可以看出，两者吻合良好。

3 热力学性质计算

基于模块化思想设计的状态方程可灵活应用于不同类型流体的热力学性质计算，在宽广的温度和压力范围均能取得良好的模拟效果，且可采用同一套分子参数。本文仅对含缔合流体及电解质溶液的热力学性质计算效果进行简要回顾，其他流体计算效果可见文献[9,12,20]。

3.1 相平衡

当某一体系处于平衡状态时，需要各相的温度、压力相同，同时各相中对应组分i的化学位相等，即：

式中，μi为组分i在不同相中的化学位，可通过SWCF(-VR)或其他热力学模型计算，上标V 和L 分别表示汽相和液相。

在根据纯流体PVT数据确定分子参数的过程中，即已完成纯流体相平衡的计算。在获得分子参数后，进一步实现二元及多元相平衡计算。对二元混合物，模拟的91 组自缔合（含一种缔合流体）体系的温度、压力和组成总体平均绝对偏差分别为0.93 K、1.05 kPa 和 0.017 3；对 40 组交叉缔合（两组分均为缔合流体）体系，其对应值分别为0.70 K、0.94 kPa 和0.013 3[13]；对40 组含离子液体体系的相平衡，其平衡压力的AAD为6.89%[14]；对含离子液体水溶液，获得的渗透系数和溶液密度AAD分别为2.49%和0.87%[11]。

二元汽液平衡的理论值和实验值的比较如图3所示。由图3 可以看出，理论模型可高精度地重现实验结果[10]。离子液体水溶液的渗透系数和密度理论值和实验值的比较如图4 所示。由图4 可以看出，理论值和实验值同样吻合良好[11]。

另一方面，借助状态方程对二元体系进行计算，可进一步推算（预测）对应多元体系相平衡，结果如图5 所示，其预测结果是基于丙酮-甲醇-乙醇两两二元性质获得的。由图5 可以看出，理论值和实验值吻合良好[10]。热力学理论模型对液液平衡和固液平衡同样有效[21]，理论值和实验值对比如图6 所示。由图6 可以看出，结果令人满意。

3.2 焓

纯流体的蒸发焓和流体混合物的混合焓均可根据热力学基本关系式和状态方程进行连接。

对纯流体，根据 Clapeyron-Clausius 方程式（8）即可获得蒸发焓ΔvapH。

对混合焓，则根据式（9）计算获得。

式中，n为物质的量；H*为相同条件纯组分的焓。纯组分蒸发焓和二元混合物苯-乙酸体系混合焓理论值和实验值比较如图7 所示。由图7 可以看出，两者吻合良好[10]。

3.3 传递性质

结合热力学和传递模型，可通过状态方程进一步计算纯流体的黏度、混合物表面张力等传递性质。 黏度和表面张力模型分别见式（10）和式（11）[1,22]。

式中，μ为黏度；z为压缩因子；k1和k2为模型参数；γ为表面张力，和分别为组分i在纯态和混合物中的表面积（根据摩尔体积计算）；φ为逸度系数；x为摩尔分数；上标S 和L 分别表示表面相和液体主体相。上述的压缩因子、逸度系数、摩尔体积（每摩尔物质所占体积）等均可通过本文介绍的热力学模型或其他状态方程得到，从而完成对应传递性质的计算。图8（a）比较了离子液体[C8mim][BF4]在不同温度下的黏度，由图8（a）可以看出，理论值和实验值吻合良好[23]。图8（b）为通过表面张力模型计算的不同流体混合物表面张力理论值与实验值的比较，结果同样令人满意。计算的8 种纯离子液体黏度AAD为0.70%，预测的87 种常规流体混合物表面张力AAD为1.82%，表面张力模型同时可用于水溶液、醇胺、聚合物溶液及合金等系统[22]。

4 网络平台

热力学模型和相平衡数据在工程实际和科学研究中均有广泛需求，但相关内容在公共网络中仅片段化存在，对全面认识和理解相平衡知识带来了不便。为此，基于多年研究积累开发了国内首个以“流体相平衡”为主题的公共网络平台（www.equilibria.cn），从基本原理、相图结构、实验技术、计算模型、实际应用、最新进展等方面对相平衡进行全面概述，并为用户提供多样化的相平衡模拟软件。

另一方面，为便利热力学数据查询，开发了一套在线数据查询系统，包括近2 000 种化合物的基本物性（分子质量、沸点、临界性质、密度参数、UNIQUAC 模型参数、标准生成焓等）、PVT数据和蒸发焓以及近5 000 组二元汽液平衡数据[8]，这些数据基本能够满足常规流程工业过程设计、模拟及优化的需求。表2 为自2016 年4 月平台开放以来的访问量统计，至2019 年12 月31 日总来访次数达到2万余次，可见平台得到了用户较为广泛的关注。

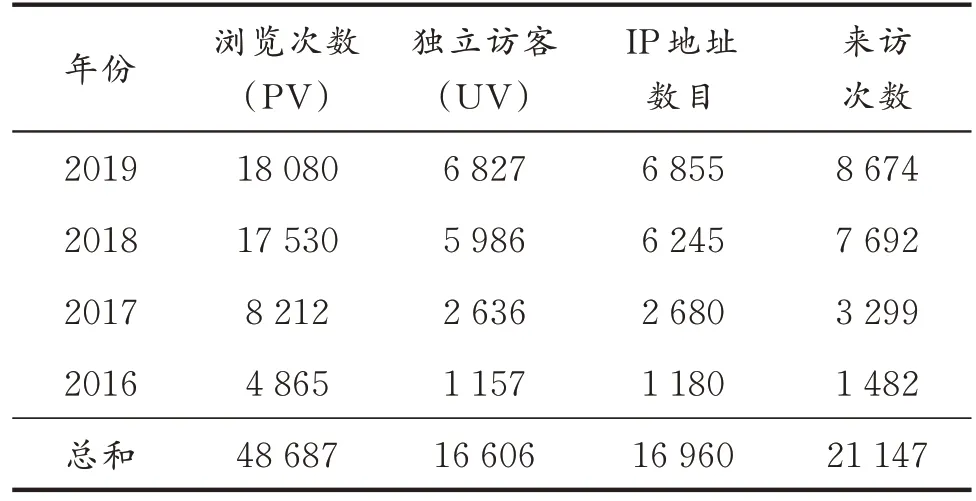
表2 网络平台受访统计

5 结 论

热力学模型和数据发展至今，理论结构日渐完善，数据累积持续增多，为流程工业运行、材料设计、能源开发等领域的一般问题解决提供了有力保障。例如，SWCF（-VR）模型基于同一套分子参数即可完成相平衡、焓、黏度、表面张力等热物性的计算，也可与密度泛函理论结合洞察介观相行为和相界面结构，为材料设计和性能调控提供指导。然而，尽管其在常规条件下可取得良好结果，但对近临界区、超低温/高压区、量子流体等热力学行为的描述仍待进一步完善，为新材料、新能源及新工艺的设计及过程开发提供有益指导。