时空稀疏贝叶斯的多通道降噪方法及在机械故障诊断中的应用

吴安定，吴加福，易灿灿

（1．温州市特种设备检测研究院，浙江 温州 325000；2.武汉科技大学，湖北 武汉 430081）

1 引言

轴承作为机械设备中关键的承载部件[1]，对其可能出现的故障做出准确的诊断有实际的应用价值。实测的机械设备振动信号有很强的非线性非平稳特性[2]，有用的特征成分容易被其他干扰成分和噪声成分所掩盖。为了有效的提取信号的故障特征，学者提出了多种信号处理方法。传统的信号处理方法的对象大多是单通道故障信号，如奇异谱分析（Singular Spectral Analysis，SSA）[3]和小波分解（Wavelet Transform，WT）[4]，SSA 通过奇异值的大小将信号分解为有用成分和噪声成分，但分解结果受噪声的水平影响较大。WT 可以有效地将信号分解为高频成分和低频成分，然而小波基的选择对分解结果影响很大。压缩感知理论[5]利用非自适应的且与稀疏基独立的观测矩阵将具有稀疏结构的高维度信号线性保距投影到低维子空间，并根据获取的投影来重构原始信号，对于信号的压缩和降噪有很好的效果。但是目前的压缩感知理论处理的对象只能是单通道信号数据，同时信号的稀疏性对于处理的结果具有决定性的影响。2008 年学者将压缩感知与稀疏贝叶斯学习（sparse bayesian learning，SBL）[6]相结合，极大的提高了信号稀疏分解的精度，并在含噪声的观测下重构出参数，从而有效提取信号中特征成分，对于单通道信号的特征提取有很好的效果。

由于单通道信号所包含的设备信息有限，不能完整的评估设备的健康状态。随着多传感器技术的发展，针对多通道信号的处理技术显得尤为重要。针对压缩感知在处理多通道信号方面存在的一些问题，提出了一种基于时空稀疏贝叶斯学习（Spatio-Temporal Sparse Bayesian Learning，STSBL）[7]的多通道信号降噪算法，将单通道压缩感知理论拓展到多通道领域，同时选用稀疏二进制矩阵作为观测矩阵，并通过K-SVD 优化学习训练规则和OMP 算法[7]求取自适应过完备字典[8]，然后利用提出的STSBL 模型获取多通道机械故障信号联合稀疏系数，最后将这些参数引入多通道压缩感知准确重构原始信号，实现信号降噪目的，提取多通道信号特征信息。为了验证提出方法的有效性，分别进行了数值仿真信号和实测的风力发动机主轴后轴轴承故障信号分析，结果表明提出的方法能较好抑制噪声的影响并有效的提取设备的故障特征成分。

2 理论描述

2.1 多通道信号压缩感知理论

由于传统得压缩感知理论针对的是单通道信号数据。因此这里将其拓展到多通道领域。假设由相同字典稀疏基D∈RN×N表示的实测的多通道原始不含噪信号X∈RN×J（N 为每一通道信号长度，J 为通道数），选择一个与D 不相干的观测矩阵 Φ∈RM×N（M＜＜N），根据线性投影算法可以实现多通道数据的同步压缩：

其中，Y=［y1，…，yJ］∈RM×J表示多通道压缩信号矩阵，V∈RM×J为噪声矩阵，Θ∈RM×J为多通道信号重构稀疏系数矩阵。Θ 中非零系数的个数即为信号X 的稀疏度。压缩感知的目的是如何从多通道压缩信号中中准确重构特征信号（X=DΘ，从而实现信号降噪过程。可以通过从式（1）中可以观察到稀疏基以及稀疏系数矩阵的获得是关键所在。

2.2 基于时空稀疏贝叶斯学习的多通道降噪算法

提出将STSBL 引入多通道压缩感知，利用单通道信号中的时间相关性和块稀疏性，以及多通道信号间的空间相关性，求取多通道信号重构稀疏系数矩阵Θ，对多通道机械故障信号进行精确重构和去噪。同时使用K-SVD 优化学习训练规则[20]和OMP 算法获得多通道信号自适应过完备字典稀疏基D，从而实现信号的准确重构。

首先设压缩多通道信号Y 可划分为为式（2）所示的块结构：

其中，B∈RJ×J和Ai∈Rdi×di分别是用于捕捉 Θ（i）每行元素空间相关性和时间相关性的待定正定矩阵，γi是用来控制Θ（i）稀疏性的待定非负参数，通过优化学习控制γi趋近于0，能有效提高块稀疏性。

根据块的划分原则，稀疏块Θ（i）间保持相互独立，则Θ 需满足式（5）所示分布：

为了准确且快速的求解A，B，λ 等参数，采用交替学习算法（alternating-learning）分别将矩阵B 和Ai处理为空间和时间白化模型矩阵，即也就是通过空间白化模型来估计参数｛γi，Ai｝hi=1，通过空间白化模型来估计参数B。在优化学习习过程中将上述时间-空间白化模型相互交替学习，直到学习算法收敛，估计出A，B，λ 等最优参数，从而求解重构稀疏系数矩阵Θ。

根据以上提出的方法，可以有效地求取过完备字典稀疏基以及重构稀疏系数矩阵，进而高效的重构出原信号，实现降噪目的。其实现过程流程，如图1 所示。

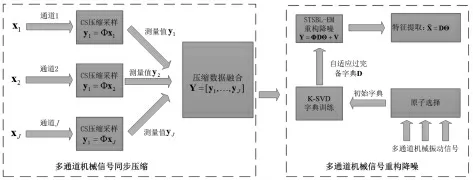
图1 基于时空稀疏贝叶斯学习的多通道降噪方法流程图Fig.1 The Flowchart of the Multiple Channel Denoising Method Based on Spatio-Temporal Sparse Bayesian Learning（STSBL）

具体步骤如下：（1）通过传感器测取多通道机械振动信号，将其分为两部分，一部分用于获取自适应过完备字典稀疏基D，一部分用于多通道压缩感知重构信号特征成分。（2）选用稀疏二进制矩阵为观测矩阵Φ 根据式（1）压缩含噪信号矩阵得到多通道压缩信号矩阵Y。（3）选取部分多通道故障信号构造初始字典，然后利用K-SVD 优化学习训练规则[20]和OMP 算法获取准确的多通道自适应过完备字典稀疏基D。（4）根据提出的基于STSBL方法求解重构稀疏系数矩阵Θ，从而准确重构多通道特征信号（X=DΘ，提取信号特征信息，完成降噪目的。

3 仿真分析

轴承作为机械设备中承载的关键零部件，当其出现故障时，其振动信号一般包含故障特征成分和冲击等其他干扰成分，同时有很强的背景噪声。构造多通道轴承内圈故障仿真信号如下：

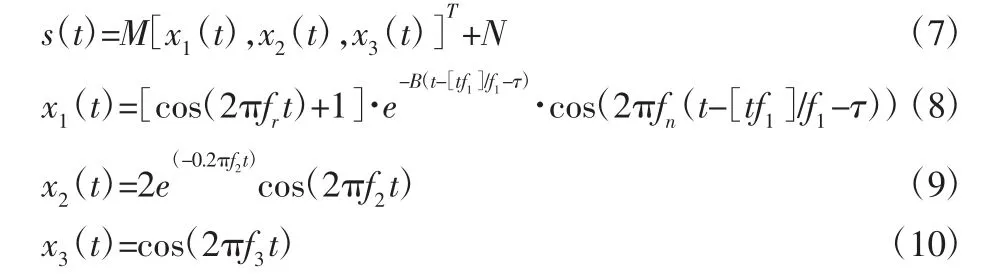
其中混合矩阵M∈R20×3用来模拟20 个通道，x1（t）是故障特征频率为f1=250Hz，且被转频为fr=20Hz 所调制的轴承内圈仿真信号，其衰减系数B=800，时延τ=0.01，fn=2000 是轴承系统的固有谐振频率；x2（t）是中心频率f2=80Hz 的冲击成分，x3（t）是频率f3=50Hz 的简谐成分，N 是各个通道水平为2 的高斯白噪声信号，采样频率和采样点分别设置为40000Hz 和40000。

为了验证自适应过完备字典的优势，选用离散余弦变换（DCT）字典作为对比分析。在训练过程中，从20 个源信号中任意选取10 通道信号以数据长度为200 进行切割，得到200 个原子，随后以此为样本进行字典训练，获得各自的字典，最后分别利用两种字典结合STSBL 方法对剩余的10 通道信号随机抽取两个通道进行重构去噪，并对比降噪效果。同时为了验证提出方法的有效性，选用WT 对抽取的两个通道信号分别进行处理，比较它们的降噪效果。各方法的分析结果，如图2 所示。其中，抽取其中两个通道含噪信号的频域图，如图2（a）所示。WT 处理的结果，如图2（b）所示。基于DCT 字典和STSBL 处理的结果，如图2（c）所示。基于自适应过完备字典和STSBL 处理的结果，如图2（d）所示。

图2 抽取的两通道数据处理结果Fig.2 The Processing Results of The Two Channel Signals Which Are Randomly Selected

由图2（a）可发现，原始信号频谱图中虽然可以找到特征频率的谐波频率，但是调制成分几乎被强噪声所淹没，导致故障特征难以识别。图2（b）是WT 的处理结果频谱图，可以观察到故障特征频率和其谐波频率以及简谐成分，但是调制边频成分依然不完整，且存在很多由红色圆圈标记峰值较高的难以解释的干扰频率成分，导致了不能准确的判断故障类型。而从图2（c）通过提出的方法处理后，内圈故障特征频率和其各谐波频率以及对应的调制边频都非常清晰，同时虽存在一些干扰频率成分，但是可以看出它们的峰值均较小，对于故障的确定几乎没有影响，此外，相比较其他两种方法，这里方法的降噪效果非常明显。因此，提出的基于自适应过完备字典和STSBL 的方法具有良好的降噪效果，能准确的提取浮躁信号中的故障特征成分。

4 实验分析

为了说明提出的方法对于实测信号的降噪性能，在现场采集风力发电机后轴承数据用于分析。该风机为功率1.5MW 的直驱式永磁风力发电机，其滚动轴承在运行的过程中出现了内圈故障。该风力发电机组主要部件及传感器测点布置，如图3 所示。图中：1H—主轴承水平方向；1V—主轴承垂直方向；1A—主轴承轴向方向。现场检测的照片，如图4 所示。

图3 直驱永磁风力发电机组结构及传感器测点布置Fig.3 Direct Drive Permanent Magnet Wind Turbine Structure and Sensor Measuring Point Arrangement

图4 现场测试照片Fig.4 Field Testing Photos

所用传感器型号为高灵敏度三轴ICP 加速度传感器PCB-356A16，数据采集卡型号为研华USB-4716。本实验选取8 个通道的风力机后轴承水平振动（1H）信号作为处理对象，信号的采样频率为1280Hz，采样点为102400。由于在实际环境中风力发电机的转速较低，其额定转速为17.3r/min，根据经验公式计算得到的轴承内圈故障也较低，本次测取的轴承的内圈故障频率为fo=7.5Hz。采用自适应过完备字典对风力机信号进行稀疏表示。在字典训练过程中，从8 个通道的源信号中任取5 个通道的信号以256 长度进行切割，得到400 个原子，再以该原子为样本进行字典训练，获得自适应过完备字典，最后利用自适应字典及STSBL 算法对另外的3 个通道的信号进行重构去噪。分析结果，如图5 所示。

实测信号的频谱图，如图5（a）所示。图中虽然可以找到故障频率以及其二倍谐波频率，但是在谱图上存在其他许多如红色圆圈标记峰值较高的干扰频率成分，导致不能直接判断内圈出现了故障。小波分析的结果，如图5（b）所示。可以发现噪声成分有了一定程度上的消减，但是提取的结果却是与故障频率成分无关的频率成分（fw=5Hz）及其谐波成分，因此，不能判断故障信息。提出的结合自适应过完备字典和STSBL 的方法降噪后特征提取的结果，如图5（c）所示。可以看见信号噪声基本被消除，特征频率及其谐波倍频凸现出来。由此可见，基于自适应过完备字典和STSBL 的方法的降噪算法去噪效果更好，而且能准确的提取故障特征成分。

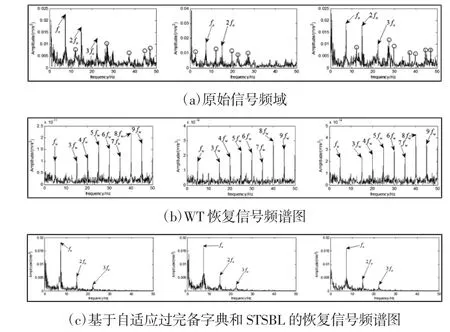
图5 实测风机轴承故障信号处理结果Fig.5 The Processing Results of Collected Fan Bearing Fault Signal

5 结论

提出了一种基于时空稀疏贝叶斯学习的多通道降噪算法，并将其应用在风力发电机轴承故障诊断中。首先介绍了多通道压缩感知模型，并对于模型中两个重要的参量稀疏基以及稀疏系数矩阵提出了估计的方法。首先将自适应过完备字典学习用于字典稀疏基的估计，然后提出基于时空稀疏贝叶斯学习确定多通道信号重构稀疏系数矩阵，从而实现多通道机械故障信号的有效降噪以及特征成分的精确重构。通过仿真信号和实测的风机轴承内圈故障信号的分析，成功地提取了故障特征成分，并对噪声有很强的抑制作用，证明了提出的方法在风机故障诊断中的实用性。