藏东南地区粗粒土三轴渗透试验研究

金建立

(1.西藏农牧学院 水利土木工程学院， 西藏 林芝 860000； 2.河海大学 土木与交通学院)

1 引言

路基是公路工程的重要受力结构，沿河路基除了受到上部荷载的作用外，还受到流水的冲刷和水的渗透作用影响，边坡受力和变形较为复杂。藏东南地区普遍分布有大量的粗颗粒混合料，该土为第四系构造运动中形成的有黏性粗颗粒土，是砾质土、风化料和冰碛土组成的复杂混合土体。研究区域为高山峡谷地形，工程中存在着大量的临水边坡，水位的变化会引起边坡内土体含水率的不断变化，渗流的发生对工程安全产生较大影响。对于边坡的渗透稳定性进行分析目前常用的方法有现场试验或室内试验，但这些试验由于试验条件的限制，很多力的因素和土体的应力状态无法充分考虑，而这些因素的存在会对土体的渗透性能产生影响，所以在研究临水边坡的稳定性时，应对其土体在复杂应力状态下的渗透性能进行研究，以期准确地把握其变形性能。

关于土体孔隙比与其渗透性能关系的研究中，Teizaghi最早提出了土体微观结构的概念；Carman在研究多孔介质的基础上提出了KC方程，描述了材料孔隙率与材料渗透系数之间的关系；龚霞等针对细粒含量和干密度等因素研究了粗粒土的渗透特性；周中等通过自制的渗透试验仪器研究了土石混合料的渗透特性，提出了适合计算土石混合料渗透系数的经验公式；邓永锋等将多种渗透系数与孔隙比的关系公式进行对比，指出已有的经验公式在logk-e坐标中呈直线关系，直线的斜率可以用土体初始孔隙比的函数进行表示；黄达等基于Copula理论建立了估算粒径范围0.1～20 mm粗粒土渗透系数的方法。

实际工程中只要合理控制土的干密度和体积，可以达到相同的孔隙率，也即不同的应力状态和边界条件下可以使土体满足相同孔隙率的要求。此时相同的孔隙比不同的应力状态，致使土体内部颗粒排列存在差异性，引起孔隙特征产生差异，也即相同孔隙率的土体其渗透性能也会不一样，说明不同应力状态下的土体渗透系数不是唯一的。关于土体渗透系数的研究，徐永福等通过室内试验，结合分形理论导出了土的渗透系数表达式，总结出了压应力与土的渗透系数的关系；罗玉龙等通过室内多相多场耦合试验总结了围压与土体渗透性能的关系；陈锦剑等通过改变围压等条件，总结了分级降压条件下的渗透系数与孔隙比的关系。可以看出，关于应力变化对土体渗透系数影响的研究虽然取得了大量的成果，但还未形成一个体系，实际渗流发生时的应力状况更为复杂，需要进行进一步的研究。

该文基于藏东南地区粗颗粒混合料，利用大三轴进行渗透系数室内试验研究，对土体设定相对复杂的应力条件，找出研究区域的粗粒混合料在复杂应力状态下的渗流特性，为藏东南地区的临水边坡和水利工程建设提供参考资料。

2 渗透系数三轴试验

2.1 土样基本性质试验

试验土样采自318国道西藏段波密至鲁朗境内102滑坡2#滑坡体，土样采集后风干至含水率小于2%方可使用。筛分试验结果见表1。

表1 试样土样颗粒特征指标

由表1可知：边坡土的粒径分布不均匀。将筛分试验计算结果与规范对比得出，102滑坡2#滑坡体的边坡土为级配不良土(SP)。根据三轴试验的试样规格，取土样的最大粒径为60 mm，筛分后的0.1 mm以下粒径土的含量为1.75%～4.33%，小于5%，根据规范规定可以将土样界定为有黏性粗粒土，为该地区路基和堤坝等工程的常用材料。根据室内击实试验确定试样的用土量为94.34 kg。

2.2 试验设计

三轴渗透试验中，分5层对试样进行装样击实。利用三轴仪器良好的围压、轴压控制性能满足试验条件，以恒定的水头对试样进行渗透试验。试验设置200、400、800、1 200、1 600 kPa共5种围压和0、0.2、0.4、0.6、0.8共5种应力水平。试验土样的最大粒径为60 mm，试样的规格为φ300 mm×600 mm，试验首先将试样渗流量调试稳定，然后对试验施加100 kPa的水头压力开始渗透试验。试验中记录各排水管的出水量、渗流时间和实时温度。

3 试验结果分析

3.1 颗粒级配对渗透系数的影响

根据上述试验方法和SL 237-1999《土工试验规程》对试验结果进行整理分析，得到试样的渗透系数如图1所示。

从图1可知:不同的颗粒级配条件下，试样的渗透系数不一样。试样的渗透系数与其不均匀系数成线性关系，不均匀系数越大其渗透性越好。试样1#粒径2 mm以下含量为42%，试样2#粒径2 mm以下含量为35.8%，试样3#粒径2 mm以下含量下降为30.8%。试样1#～3#细粒含量依次减小，在围压为200 kPa时对应的渗透系数分别为7.56、9.27和11.38，同样的试验条件下细粒含量较高试样渗透系数较小，可见级配对同一围压下试样的渗透系数有较大的影响。产生这种情况主要是因为细颗粒在土中起到填充孔隙的作用，细粒较少的试样粗颗粒间的孔隙不能被充分填充，形成较大的孔隙率，渗透水相对流通通道较多，导致土样的渗透系数增大，与黄达等的研究结论一致。

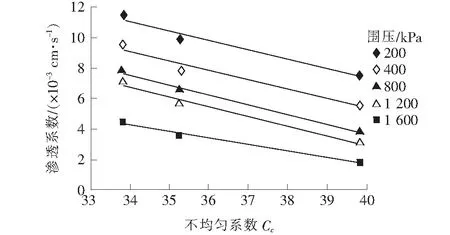
图1 不同Cc下的渗透系数

3.2 围压与渗透系数的关系

将三轴渗透试验结果点绘应力水平为0时的渗透系数与围压的关系曲线，如图2所示。

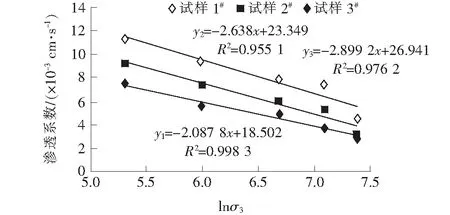
图2 不同围压下试样的渗透系数

由图2可知：试样的渗透系数与试验围压的对数成直线关系，渗透系数随着围压的增加逐渐减小，主要是因为高围压作用下土体内水和气的排出量较多，致使土颗粒的重新排列度较高，土体内的孔隙体积减少量大，降低了水的流通通道量，所以渗透系数随着围压的增加而降低。试样1#～3#中的细粒含量依次减少，相应的渗透系数依次增加，说明细颗粒的含量对试样渗透特性影响较为明显。主要是因为细颗粒能够较好地填充粗颗粒所形成的孔隙，减少渗流水的渗流通道，表现为渗出水量的减小，渗透系数的降低，这与文献[14]、[15]的研究结论一致。将试验围压取自然对数进行拟合，由图2中的拟合公式可知：拟合后的试样渗透系数与围压成一次曲线关系，相关性系数均大于0.95，说明围压对渗透系数影响具有一定的规律性，可以用一次函数表示。

3.3 应力水平与渗透系数的关系

图3为试样1#的应力水平与渗透系数变化曲线。

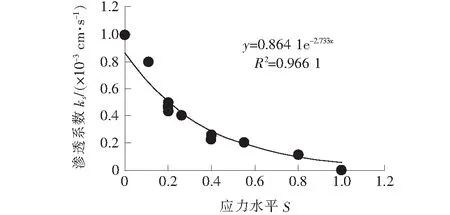
图3 试样1#ks-S关系曲线

由图3可知，试样的渗透系数与其应力水平成指数关系。拟合相关性系数达0.966 1，可见拟合的契合度较高。将图2、3 的拟合关系式进行结合整理可得渗透系数、应力水平及围压的关系式：

ks=(a+blnσ3)ecS

(1)

式中：ks为渗透系数；S为试样的应力水平；a、b、c为拟合曲线系数；σ3为试验围压。

为了验证拟合公式的正确性，该文采用Abaqus软件建立三轴试验模型，用式(1)计算围压为400、800、1 200、1 600 kPa共4情况下的渗透系数和有限元模拟值进行对比(图4)，并对两种方法得出的渗透系数值进行相关性分析，由图4可得：两者的Person相关性系数值为0.942>0.8，属于高度相关，可见拟合公式是可靠的，在缺少试验条件的情况下可以用该拟合公式近似进行相关渗透系数的估算。

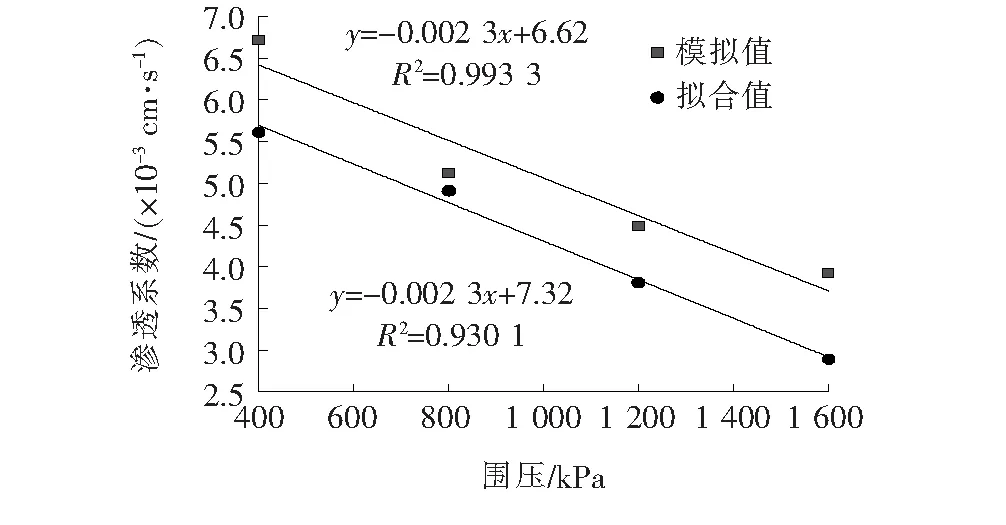
图4 渗透系数模拟值和拟合值对比图

4 结论

(1) 研究区域的土样颗粒对其渗透系数有显著的影响，一定条件下细颗粒越多渗透性能越差，表明该区域土体的渗透性能受其级配组成影响较大，较好的级配可以改善其渗透性能，减小渗透对工程的破坏。

(2) 土样的渗透系数与围压经拟合后呈线性关系，渗透系数与其应力水平成指数关系。

(3) 通过拟合运算得出了土样渗透系数、应力水平及围压的拟合关系式，公式可靠可行，在缺少试验条件时可以用该拟合式近似进行相关渗透系数估算。