地铁盾构隧道近接下穿既有铁路隧道加固范围优化设计
——以南宁地铁4号线下穿既有槎路隧道为例
唐志辉
(中铁第六勘察设计院集团有限公司, 天津 300308)
0 引言
近年来,随着我国城市轨道交通的发展,地铁路网愈发密集,出现了较多的地铁隧道下穿既有建(构)筑物的情况。当新建地铁隧道下穿既有运营铁路隧道时,一旦处理不当,不仅会影响既有结构的服役安全,严重时还会波及铁路轨道的平顺性,危及列车运行安全。
目前,针对地铁隧道下穿既有隧道方面的研究已经有了较多的成果,例如: 胡众等[1]依托合肥地铁1号线下穿既有城市公路隧道工程,通过FLAC3D建立了盾构隧道掘进施工力学行为计算模型,分析得到了既有隧道结构及新建隧道的应力、应变分布规律,并提出了相应的防护措施;毛新颖等[2]依托地铁隧道下穿桂庙路公路隧道工程,研究了盾构下穿近接公路隧道的影响规律;孙连勇等[3]以济南轨道交通R3线下穿胶济铁路线桥梁和路基工程为依托,采用ABAQUS模拟了主动加固和不主动加固条件下桥墩和路基的沉降情况,并指出采用钻孔灌注桩的加固效果较好;傅洪贤等[4]以某一铁路客专隧道超近距下穿运营地铁隧道工程为依托,提出了超近距离下穿运营地铁隧道的微振爆破技术;徐干成等[5]结合北京地铁14号线下穿京津城际铁路隧道工程,开展了数值模拟研究,结果表明,对下穿段一定范围内的土体进行加固可有效控制既有铁路的沉降变形。
总之,较多研究者针对该技术问题开展了丰富的理论与实践研究[6-9],对工程建设起到了极大的促进作用。但在盾构隧道下穿既有隧道工程的加固技术研究方面,一般是基于实践经验,且出于安全的考虑,采取了相对较为保守的工程措施,虽能够最大限度地保证施工的安全,但也给工程实际带来了较大的施工难度或者造成了一定的资源浪费,从整个社会发展以及行业水平的提升来说,仍可以进行深入研究,以求效果可控、资源节约。基于上述原因,结合工程实践,本文针对盾构隧道下穿既有铁路隧道工程的合理加固范围进行了研究。
1 工程概况
南宁地铁4号线那历村站—那洪立交站区间沿那洪大道东西走向敷设,线路埋深12.4~18.1 m,采用盾构法施工,管片外径为6.0 m,内径为5.4 m,壁厚0.3 m,管片宽1.5 m。盾构穿越的地层依次为泥岩、泥质粉砂岩。
该地铁区间隧道下穿南环线槎路隧道,平面交角约为83°,地铁隧道与槎路隧道上下净距仅2.644~2.725 m,位置关系见图1。槎路隧道于2002年5月1日竣工,全长2 230 m,为单洞单线货运隧道,隧顶埋深约8.16 m。槎路隧道采用新奥法施工,下穿段设计为Ⅱ类复合衬砌,其初期支护厚0.2 m,内部钢架间距为1.0 m,采用16#工字钢;二次衬砌厚度为0.45 m,主筋直径为22 mm,双排布置,纵向间距为250 mm。
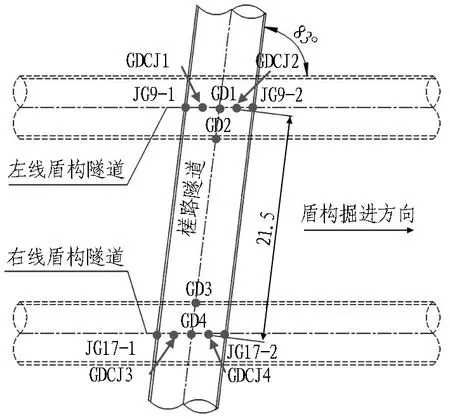
(a) 平面位置关系
槎路隧道上部为含黏性土圆砾层,下部位于泥岩、泥质粉砂岩层中,下穿段夹层土主要为泥岩,右线局部存在层状泥质粉砂岩,地层概况见表1。区间下穿段水位埋深4.90~6.90 m,孔隙性潜水主要在含黏性土圆砾层中,为本区间的主要含水层,含水量大,碎屑岩类孔隙裂隙水主要在泥质粉砂岩层中。

表1 地层概况
2 工程重难点及应对措施分析
2.1 重难点分析
结合第1节的工程地质、环境条件进行分析可知,工程交叉段施工存在以下重难点:
1)地质条件复杂。槎路隧道上半断面位于含水量大的含黏性土圆砾层中,围岩自稳性差,受扰动后易坍塌;地铁隧道位于泥岩层,该层黏粒质量分数高,盾构施工时易黏刀盘,结泥饼,土舱压力较难控制;泥质粉砂岩层的泥质胶结较差,遇水扰动后易破碎失稳,盾构掘进易产生坍塌,且涌水量可能较大,严重时会引发开挖面失稳和地面沉陷。
2)周边环境复杂。槎路隧道铁路为货运线,设计行车速度为120 km/h,是钦北防重要的铁路运输干线,年货运量达25×106t,下穿期间必须保证正常运营。这对铁路运营下隧道结构、铁路轨道及地表沉降等要求非常严格。根据相关规范及工程经验[10-11],既有铁路隧道变形控制标准见表2。作用在轨枕上的铁路列车活荷载如图2所示,其中,z为荷载系数,在本文中取1.2。
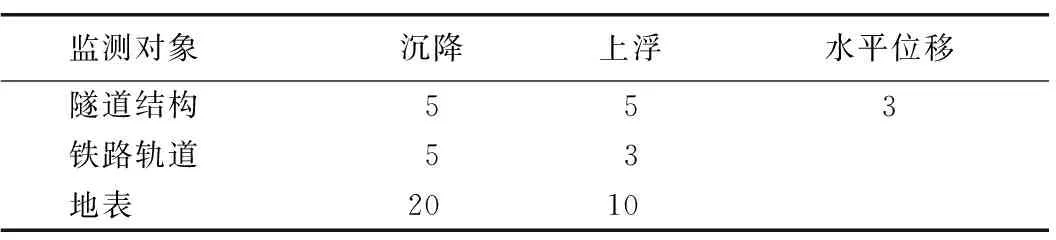
表2 既有铁路隧道变形控制标准

集中荷载的单位为kN,均布荷载的单位为kN·m-1。
3)既有隧道服役现状差。槎路隧道衬砌结构常年漏水,衬砌壁后存在空洞,围岩承载拱效应差,对盾构下穿施工作业较为敏感。
4)紧邻近接施工。4号线区间隧道与槎路隧道最小净距仅2.7 m,且该下穿段距离那洪立交站小里程接收端头只有24.7 m,施工过程中既要保证盾构出洞安全,又要保证既有铁路正常运营。
2.2 应对措施分析
为应对施工过程中存在的重难点问题,结合既有实践经验,拟对交叉段一定范围内的岩土体进行注浆加固处治(加固范围设计如图3所示),一方面提高周围岩土体本身的承载能力,另一方面在既有隧道底部位置形成一层具有一定刚度和强度的保护壳,然后再进行新建地铁隧道的盾构掘进。其中,对于加固圈施工,在槎路隧道下方采用钢花管对边墙底部衬砌背后进行注浆加固,钢花管呈1.0 m×1.0 m梅花形布置,墙角及仰拱部位可适当加密;盾构隧道通过预留注浆孔位置时,打设钢花管进行二次注浆,弥补盾构掘进产生的地层损失;注浆材料以添加外加剂的复合型浆材为主,辅以普通水泥-水玻璃双液浆和普通水泥单液浆,复合浆材主要由水泥、水玻璃及抗分散型外加剂组成。
对于加固范围,包括既有铁路隧道横断面方向上的加固厚度和轴向加固长度,目前还没有明确的量化方法。为此,围绕该问题,建立数值模型,分析不同加固范围时系统的安全状态(采用强度折减法),通过多工况的规律性分析,寻找合理的加固范围。
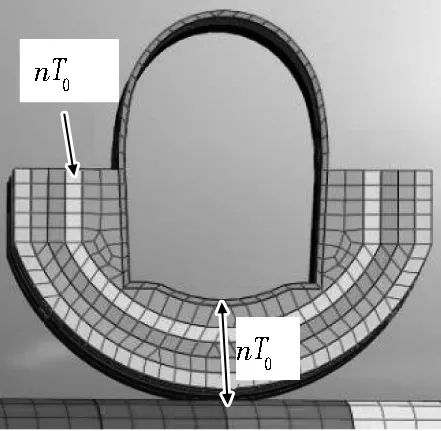
(a) U型加固圈厚度
3 基于强度折减法的近接工程加固范围分析
区别于简单的构件,隧道结构为超静定结构体系,无论是围岩的稳定性分析还是结构的安全性分析,往往都无法采用单一的物理指标来表征其力学状态,这给隧道工程的结构分析、设计计算带来了极大的不便。目前,已有研究者针对该问题开展了积极的探索,郑颖人等[12]和唐春安等[13]将边坡工程中应用较多的强度折减法[14]引入到隧道工程安全性分析中,提出用折减系数来表征隧道施工过程中围岩稳定或结构的安全程度,如此使得隧道安全性分析概念更加直观,取得了良好的应用效果。借鉴该思路,提出基于强度折减法的隧道近接工程施工合理加固范围分析方法,基本思路为:
1)建立隧道近接施工工程数值模型。在模型建立的过程中,应综合考虑后续加固范围,即将后续讨论的多种加固范围工况预先设定好对应的网格单元,后续计算分析时,无须重新建模,仅需要调整拟加固区域的物理力学参数。
2)根据相关规范或设计要求,确定分析对象在施工扰动过程中应控制的物理指标,如既有隧道的结构变形、轨道变形、拟建隧道的结构变形等。
3)拟定若干种加固范围工况,如不同的加固厚度、加固长度等,并根据实践经验或前期试验,获取加固后加固区域地层的物理力学参数。
4)针对每一种加固范围工况,开展强度折减法模拟计算,提取出各控制物理指标随折减系数的变化规律。

(1)

6)以此类推,计算得到所有加固范围工况(如m种工况)的系统综合安全系数F(i),i=1,…,m。由此,便可建立加固范围与系统安全系数之间的关系,进而确定系统的较优加固范围。
4 依托工程加固范围优化设计
4.1 建立数值模型
基于Midas GTS NX软件,建立数值模型,模型沿区间隧道开挖方向长80 m,宽100 m,高50 m,如图4所示。

(a) 模型三维立体图
模型中,盾构加固圈厚0.2 m,管片厚0.3 m;铁路轨道采用一维单元近似模拟;轨枕长2.6 m,厚0.2 m;铁路初期支护厚0.2 m,二次衬砌厚0.45 m。为简化计算,二次衬砌、道砟和轨枕之间采用共节点连接,暂未考虑接触。周边地层共分为3层,从上到下依次为砾石填土(厚3.5 m)、含黏性土圆砾(厚8.0 m)、泥岩(厚38.5 m)。模拟中岩土体材料本构采用摩尔-库仑模型,其余结构均设置为线弹性材料,模拟计算参数见表3。
结合施工组织,区间隧道开挖步的间距为4 m,铁路隧道采用一次性开挖支护。施工步骤为初始地应力平衡—铁路隧道开挖及支护—地层加固—位移清零—区间隧道开挖—管片支护—管片背后注浆。

表3 模拟计算参数
4.2 加固范围工况设置
如图3所示,在铁路隧道周边设计U型加固圈,加固范围为拱腰至仰拱底,每一层加固圈的厚度为0.2T0(T0=2.7 m),同时沿隧道纵向设置初始加固长度为S0(S0=21.5 m),每次在盾构隧道两侧增加2D(D=6 m)加固区,具体工况设置见表4。其中,0.8T0和S0+4D为对比分析采用的基本工况。

表4 加固范围计算工况
4.3 基于强度折减法的地层加固后铁路隧道安全性判据讨论
选取0.8T0和S0+4D作为标准工况,基于强度折减法对该加固工况下的铁路隧道系统安全系数进行试算。以隧道结构沉降变形为例,对系统安全性判据进行讨论,隧道最大沉降随折减系数的变化曲线如图5所示。由图5可知,随着折减系数的增加,隧道结构最大沉降起初增加较缓慢,当超过2.6时呈指数性增长。根据唐芬等[15]、Pantelidis等[16]基于边坡稳定性的研究成果可知,可以将特征点发生位移突变时作为围岩失稳的判据,且该方法已被唐春安等[13]、郑颖人等[17]作为判断隧道围岩稳定性的依据。则对于该工程,采取加固措施后隧道围岩稳定性的安全系数可取2.6。

图5 隧道最大沉降随折减系数的变化曲线
对于边坡来说,在临界条件下能保持稳定即可,然而对于区间下穿铁路隧道的实际工程,单纯以特征点突变作为隧道施工安全性的判据存在一定的局限性。在下穿铁路隧道过程中不仅需要保证铁路隧道结构的安全,还要保证其满足使用需要。从图5可以看出,在折减系数取2.6时,铁路隧道的最大沉降约25 mm,已经大大超过了表2中的控制值。为此,提出满足控制标准的区间下穿铁路隧道施工安全系数最大折减系数这一方法,即可得到在隧道结构控制标准下铁路隧道系统的安全系数为2.0。同理,可得到以轨道沉降和地表沉降变形标准作为控制条件时,铁路隧道系统的综合安全系数分别为2.1和2.2。
4.4 加固范围优化
通过安全系数对比可知,隧道结构控制标准是最为严格的,因此选取隧道结构控制标准来计算铁路隧道系统综合安全系数。经计算,可得到不同加固厚度、不同加固长度下区间隧道下穿铁路隧道的安全系数变化曲线,结果如图6所示。对图6分析可知:
1)随着U型加固圈厚度系数的增加,区间下穿铁路隧道的安全性系数快速增大,在加固圈厚度系数小于0.6时,加固效果随着该系数的增加明显提升;当加固圈厚度系数大于0.6后,安全系数增长缓慢,表明此时再过多提升加固圈厚度对安全系数的作用不明显。另外,考虑到加固圈厚度系数为0.4~0.8时,相比于不同加固圈长度系数下安全系数稳定时的变化量,不同加固圈厚度系数下安全系数变化量仍较大,出于安全考虑,建议加固圈厚度系数取0.8。
2)随着纵向加固长度的增加,区间下穿铁路隧道的安全系数开始呈陡增趋势,当加固圈长度系数大于4时,变化趋于平稳,与加固圈厚度系数对安全系数的影响变化趋势相似,建议加固圈长度系数取4。
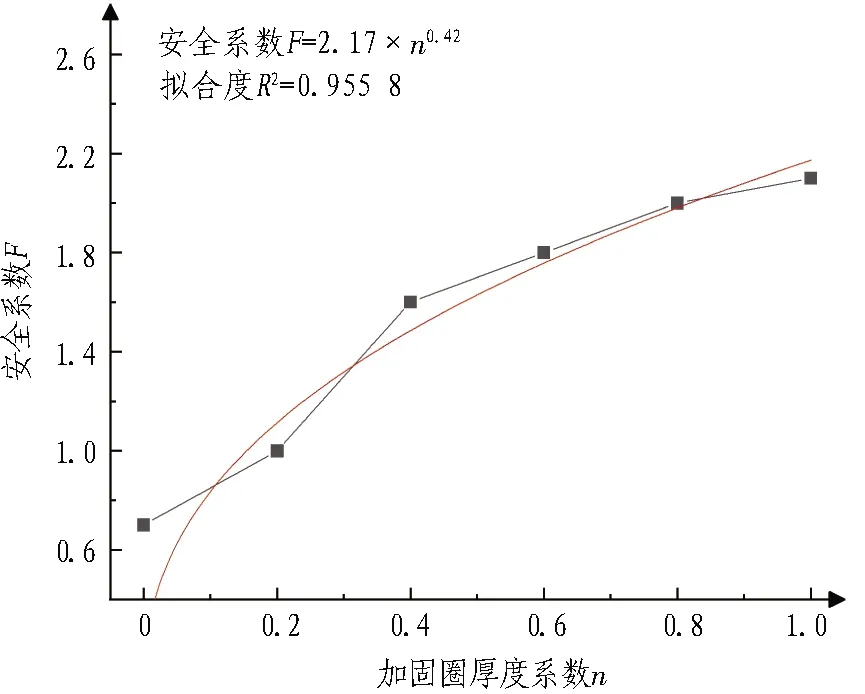
(a) 不同加固厚度
采用幂函数对不同加固圈厚度系数下铁路隧道的安全系数F进行拟合,可得
F=2.17×n0.42。
(2)
将n=T/T0代入上式,并整理得
(3)
同理,可得加固长度与既有铁路隧道安全系数的函数关系:
(4)
式(3)和式(4)即为该工程条件下基于交叉段系统安全系数的既有铁路隧道加固厚度和加固长度经验公式。实际应用时,仅需确定设计安全系数,便可根据地铁隧道与既有隧道的上下净距以及地铁隧道的水平净距确定满足控制要求的既有隧道周边加固范围。然而该公式仍有一定的局限性,既有隧道的变形和应力响应与既有隧道的断面面积、断面形式以及地铁隧道的间距、断面面积和开挖方法等因素均相关;同时,依据规范及相关经验可知,在地质条件较好以及当地铁隧道与既有隧道距离较远时,隧道相互之间的影响是较小的,若仍用式(3)和式(4)对既有隧道进行加固,显然是不合理的。综上所述,目前式(3)和式(4)仅适用于类似地质情况下盾构隧道近接下穿既有隧道工程,下一步可结合更多的工程案例和不同的工程地质条件进行深化研究,对经验公式进行补充及优化。
根据前述模拟分析,针对该工程实际情况,对下穿槎路隧道区段,预定义系统综合安全性系数为2,则根据式(3)和式(4)分别估算得到槎路隧道的加固圈厚度为2.2 m,长度为36.5 m。
5 加固效果分析
为对比分析和验证加固方案的合理性,对既有结构的变形情况进行了模拟计算和监测(监测点具体位置见图1)。未加固时既有铁路隧道沉降模拟计算结果如图7所示。加固后既有铁路隧道结构沉降监测时程曲线如图8所示。

(a) 隧道结构
由图7和图8可知: 1)未加固时既有铁路隧道结构最大沉降约为6.1 mm,铁路轨道最大沉降约为5.2 mm,与变形控制标准(见表2)对比可知,在未加固时进行施工存在较大的风险。2)加固后,既有铁路隧道侧墙及拱顶最大竖向沉降约为2.5 mm,轨道最大竖向沉降约为0.8 mm,相比于未加固时分别降低了约59%和85%,且均未超过控制值,可见采取的加固方案是有效的。

(a) 拱顶
6 结论与建议
1)加固圈厚度系数(或加固圈长度系数)与系统的综合安全系数呈幂函数关系。
2)拟定的加固方案能有效控制既有上伏铁路隧道的沉降变形,各项关键指标满足相关规范控制要求。
3)本文提出的公式仅适用于类似地质情况下盾构隧道近接下穿既有隧道工程,下一步需结合更多的工程案例和不同的工程地质条件进行深化研究,对提出的经验公式进行补充及优化。另外,需进一步研究不同地质条件下地铁隧道在不同间距、不同断面面积及施工方法下下穿不同断面既有隧道时的加固范围优化设计。

