汕头海湾隧道复合地层超大直径泥水盾构掘进参数预测研究
范文超, 孙振川, 李凤远, 张 兵, 陈 桥, 王发民, 王 凯
(1. 盾构及掘进技术国家重点实验室, 河南 郑州 450001; 2. 中铁隧道局集团有限公司, 广东 广州 511458)
0 引言
盾构施工因安全、高效、环保等优点,已广泛应用于隧道工程。盾构掘进参数能反映地质环境及盾构工作状况,它们之间存在复杂的非线性关系。合理的掘进参数可提高盾构掘进效率,节约施工成本,保障施工安全。
目前,国内外学者已对盾构掘进参数进行了大量研究。在理论模型方面: Zare等[1]基于预测掘进速度和滚刀损耗的NTNU模型,对掘进过程中时间和成本进行了评估并取得良好效果; Zhao等[2]基于CSM预测模型研究了盘形滚刀能量输入与岩体能量输出的效率比,实现以最小能量效率进行开挖。在掘进参数相关性研究方面: 张莹等[3]根据施工数据研究了盾构掘进参数与地质参数之间的关系; 魏新江等[4]研究了盾构掘进参数与地表沉降之间的关系; 陶冶等[5]根据SPSS软件研究了盾构掘进参数与掘进效率之间的关系; 张志奇等[6]通过多元统计分析方法研究了盾构掘进速度和刀盘转矩之间的关系; 李杰等[7]通过多元非线性回归方法建立了盾构掘进速度模型。
在预测方法方面: 国内,何然[8]采用Elman-PSO耦合智能算法建立了泥水盾构掘进参数智能预测系统,实现气舱压力预测; 周冠南等[9]构建了基于遗传算法的BP神经网络智能反分析系统(GA-BP),反演隧道围岩参数并预测变形; 李杰等[10]建立了盾构掘进速度的多元线性和非线性预测模型,对施工周期和成本进行评估; 王传俭[11]结合填海区复杂地层,建立了基于Python语言的BP神经网络模型,预测盾构掘进参数; Chen等[12]采用小波神经网络、广义回归神经网络及随机森林等机器学习方法,对地质条件、掘进参数和隧道几何形状进行分析并预测地表沉降量; Su等[13]通过研究UCS、BTS、CAI、掘进速度及刀盘转速等参数,建立了盘形刀具磨损预测模型。国外,Yagiz等[14]采用粒子群算法、Ghasemi等[15]采用模糊逻辑理论方法、Mahdevari等[16]采用支持向量回归方法、Delisio等[17]采用多元回归分析方法,对盾构掘进参数进行预测研究,取得了良好效果。
国内外关于盾构能耗的研究较少,因大型盾构耗电量大,施工周期长,消耗巨大能源,因此研究盾构能耗意义重大。Li等[18]通过计算矿山法隧道中每m碳排放量研究盾构能耗; 赵伟伟[19]通过研究盾构刀盘驱动系统来降低掘进过程中的刀盘能耗; 李乔松等[20]根据地层及掘进参数采用排放系数法计算隧道施工过程中的实时能耗和碳排放; 陶冶[21]采用SVM方法挖掘盾构掘进参数之间的内在关系来预测刀盘能耗; Zhou等[22]将最小二乘支持向量机(LS-SVM)和粒子群优化(PSO)相结合,通过混合能耗分析法建立能量消耗与识别因子之间的关系来分析刀盘能耗。
综上所述,关于盾构掘进参数的研究,国内外主要集中在TBM和土压盾构等小直径盾构,泥水盾构及大直径盾构研究较少;穿越岩石、砂层及黏土层等单一地层研究较多,复合地层研究较少;关于掘进速度预测研究较多,其他掘进参数尤其是刀盘能耗及平均泥水压力预测研究较少;研究的掘进参数较为单一,对多种掘进参数综合研究较少。
本文结合汕头海湾隧道工程,建立基于BP神经网络的复合地层超大直径泥水盾构掘进参数预测模型,采用神经网络挖掘掘进参数之间的内在关系,定量预测刀盘转矩、刀盘能耗和平均泥水压力。由于神经网络自适应性好,探寻非线性关系能力强,可以更深入挖掘数据之间深层次关系,为掘进参数优化、预测和控制提供依据,为安全高效施工提供保障。
1 工程概况
汕头海湾隧道工程全长6 680 m,盾构段长3 047.5 m,海域盾构段依据海床标高采用-2.9%、-0.3%、0.3%、3.0%的“V”型纵坡形式。隧道外径14.5 m,采用直径15.01 m(东线)及15.03 m(西线)超大直径泥水盾构,盾构总推力达220 000 kN,额定转矩超过42 000 kN·m。
隧道地层断面如图1所示。工程地质复杂,包含填筑土、淤泥、淤泥质土、淤泥混砂、粉细砂、粉质黏土、中砂、粗砂、砾砂、砾质黏性土、微弱中全风化花岗岩等多种地层,还包含砂土液化、软土震陷、花岗岩球状风化体、基岩突起、有害气体等不良地质。工程地质勘测区内分布4个主要含水层: 粉细砂层,中粗砂、砾层,中粗砂、砾砂层和风化岩层。基岩突起段RQD=55%~78%,层顶高程为-34.72~-27.46 m,层底未揭穿,揭露厚度为1.10~9.00 m,饱和单轴抗压强度为41.7~214 MPa,抗拉强度为2.02~9.35 MPa。此外,工程可能存在结泥饼、隧道漏水、海水倒灌、不明孤石、涌泥突水等一系列问题,因此,选择合理的掘进参数,根据掘进参数及时发现潜在问题非常重要。

图1 汕头海湾隧道复合地层断面图(单位: m)
2 主要掘进参数及相关关系
盾构掘进参数反映地层特性及施工状况,受地质水文、盾构设备及人为操作等影响,合理的掘进参数可提高掘进效率,避免发生事故。泥水盾构主要掘进参数有总推力、刀盘转速、贯入度、刀盘转矩、掘进速度、刀盘挤压力、刀盘电流、刀盘能耗、同步注浆量、平均泥水压力等,可表征当前泥水盾构工作状态。由于泥水盾构掘进参数较多,各掘进参数之间关系更为复杂。
为分析各掘进参数之间的相关程度,通常采用相关系数法,又称皮氏积矩相关系数(表征2个现象之间相关关系密切程度的统计分析指标)。
(1)
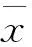
根据隧道施工数据,选择700环复合地层超大直径泥水盾构的10个主要掘进参数,根据式(1)分别相互计算皮氏积矩相关系数,计算结果如表1所示。
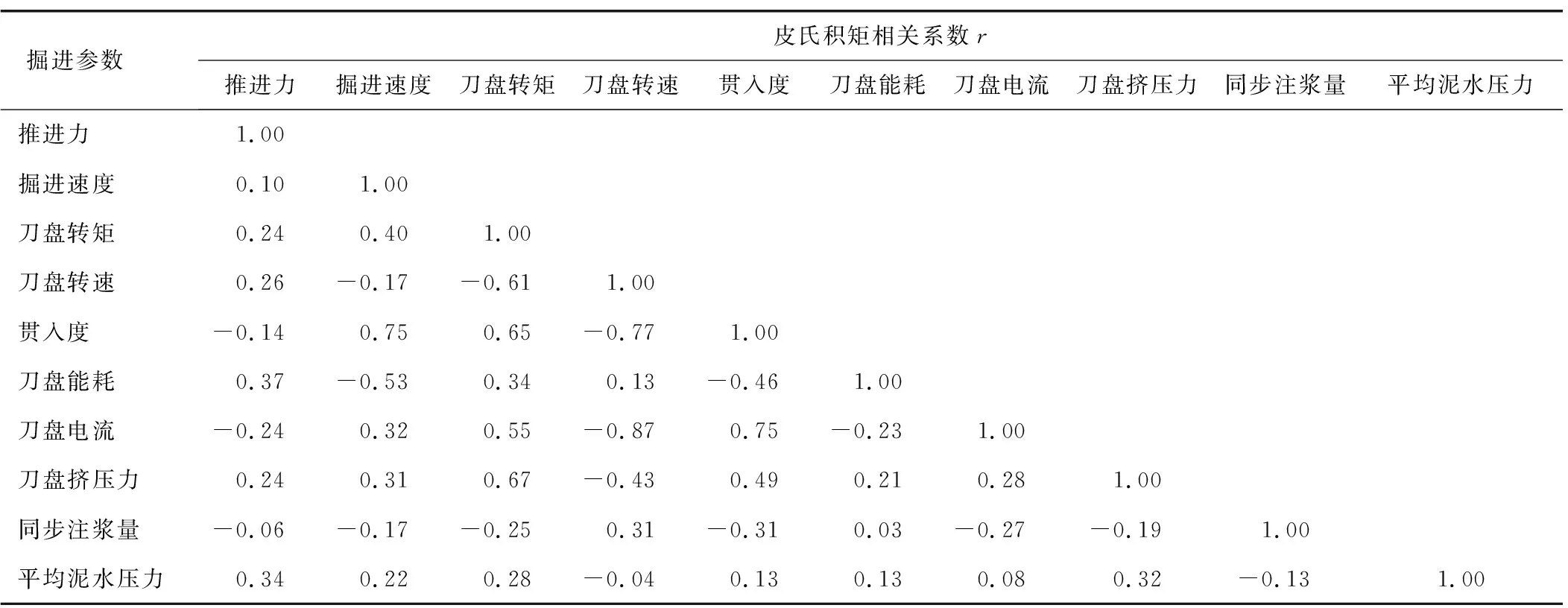
表1 各掘进参数之间的皮氏积矩相关系数
由表1可知,贯入度和掘进速度、刀盘转速的皮氏积矩相关系数分别是0.75和-0.77,刀盘电流和刀盘转速的皮氏积矩相关系数为-0.87,r绝对值较大表明它们具有良好的线性相关性。刀盘能耗和平均泥水压力等其他掘进参数之间的皮氏积矩相关系数r绝对值较小,表明它们之间相关关系不大,或者说采用皮氏积矩相关系数难以表明它们之间的关系。这是由于地质复杂,超大直径泥水盾构掘进参数之间的规律难以寻找,需进一步深层次寻找各掘进参数之间的关系。
3 神经网络预测模型
3.1 神经网络简介
神经网络是挖掘数据之间深层次复杂关系的方法,可找到输入参数与输出参数之间隐含的内在关系。BP神经网络(back propagation)又称误差反向传播神经网络,是神经网络的重要组成部分,结构简单,自适应能力强,已广泛应用于函数逼近、模式识别、信息分类预测等多种领域。
BP神经网络属于有监督学习方式,由输入层、输出层和隐含层组成。隐含层包含多层网络,层与层之间为全连接方式,同一层神经元之间没有联系。BP神经网络结构如图2所示。当确定神经网络输入数据和输出目标,每层神经元都会从该层网络的输入层获取输入值并产生连接权值向后传播,目标方向是使输出层实际输出值与目标输出值之间误差最小,随后反向传播学习修复连接权值,直至误差达到训练要求或达到学习次数,训练结束。
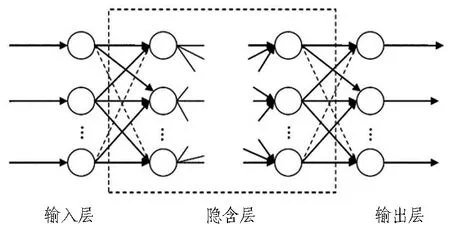
图2 BP神经网络结构
支持向量机、神经网络和深度学习等方法都已应用于回归预测研究。相比于支持向量机,BP神经网络具有更复杂的智能处理能力和非线性处理能力,网络结构设计可利用建模者经验知识获取更优模型,更广泛地应用于回归预测研究;BP神经网络本质是挖掘数据之间内在关系,对样本所有因子进行加权训练,更适用于大量数据研究,自适应能力强。相比于深度学习,BP神经网络结构简单,没有复杂的卷积层和降维层,隐含层层数少,学习训练函数少,学习训练周期短;BP神经网络没有特征学习部分,特征由人工输入,从特征到映射即输入到输出,忽略非必要特征,偏向于实际工程,预测精度已基本满足工程需求。
3.2 确定BP神经网络结构
根据《智慧盾构TBM工程大数据平台》采集的现场施工数据,选取汕头海湾隧道复合地层超大直径泥水盾构700环掘进数据作为研究对象。盾构主要掘进参数中,刀盘转矩反映地层硬度,是受到前方土体阻力产生的被动响应参数,计算复杂;刀盘驱动系统额定功率高,正常掘进时驱动功率远远小于额定功率,存在很大节能潜力,通过掘进参数预测刀盘能耗将大大提升效率;泥水压力设置不当易发生泥水劈裂、海水倒灌等事故。因此,构建神经网络预测模型时将刀盘转矩、刀盘能耗、平均泥水压力3个参数作为输出参数,将推进力、掘进速度、刀盘转速、贯入度、刀盘电流、刀盘挤压力、同步注浆量7个参数作为输入参数。
3.2.1 确定BP神经网络层数
BP神经网络结构简单,一般3层网络即可满足预测模型需求,即输入层、输出层和隐含层。本文输入输出参数一共10个,数量较少,选取3层网络建立预测模型。
3.2.2 确定BP神经网络神经元数目
BP神经网络神经元数目和实际输入输出参数有关,输入层、输出层神经元数目分别等于输入、输出参数数目,因此,本文输入层、输出层神经元数目分别为7和3。
隐含层神经元数目十分重要,数目少则网络学习能力弱,训练时间长;数目多则网络学习能力强,但将挖掘出数据之间非规律特性,导致过拟合而阻碍实际应用。因此,隐含层神经元数目需根据经验公式(2)—(4)确定在一定范围,再进一步试验寻找最优数目。
(2)
(3)
m=lbn。
(4)
式(2)—(4)中:m、n、l分别为隐含层、输入层、输出层的神经元数目;a为范围1~10的常数。
首先使用上述经验公式初步计算隐含层神经元数目为3~13,进一步在后续的模型试验中确定最优数目,然后确定BP神经网络结构。
3.2.3 确定BP神经网络函数
BP神经网络输入层、输出层及隐含层之间的函数有传递函数、学习函数和训练函数。选择合适函数将大大降低训练时间,提高训练精度。
1)传递函数:又称激活函数,模拟神经元非线性转移特性,主要有用于输入层的对数logsig函数,用于输入层、输出层的双曲正切tansig函数,用于输出层的线性purelin函数。
(5)
(6)
式(5)—(6)中: 传递函数定义域x范围为(-∞,+∞); logsig(x)和tansig(x)值域分别为(0,1)和(-1,1),并且都是可微函数。
2)学习函数: 使神经网络权值阈值梯度下降的learngd函数,以及使神经网络权值阈值产生带动量梯度下降的learngdm函数。
3)训练函数: 包括traingd、traingdm、trainrp、trainlm、traincgb、trainscg、traingdx、traincgf、traincgp、traingda、trainsog、trainbfg、trainoss、trainbr函数等。训练函数因本身特性适用于不同网络模型,具体选择时需在训练过程中进行误差评估。
4)平均均方误差MSE: 评价神经网络预测精度。多重相关系数R表示神经网络实际输出值与目标值之间的关联性,R越接近于1表示关联性越强,神经网络预测效果越好。
(7)
(8)
式(7)—(8)中:di为目标输出值;oi为实际输出值;N为测试样本数目。
5)数据归一化预处理: 因各掘进参数数量级不一致,为提高数据精确度,在建立神经网络预测模型之前,需对数据进行预处理。采用数值统计分析方法中归一化方法提高神经网络的收敛速度,将各掘进参数的数值转换到[-1,1],防止输出向量出现过拟合。
(9)
(10)

6)其他参数: 神经网络初始权值选取-1~1之间较小随机数,学习率选取0.01,远离性能曲面鞍点有利于神经网络收敛;最大失误次数设为6次,最大训练次数设为1 000次,学习训练精度设为0.01,具体参数值需根据实际模型进一步优化。
3.3 建立预测模型
通过上述分析,神经网络预测模型初步选取1层隐含层,隐含层神经元数目为3~13,初始选8个进行试验,输入、输出参数分别为7个和3个,传递函数3种,学习函数2种,训练函数14种,排列组合选取112组函数进行误差对比试验以选取最优预测模型。编写程序建立预测模型,预测模型算法流程如图3所示。
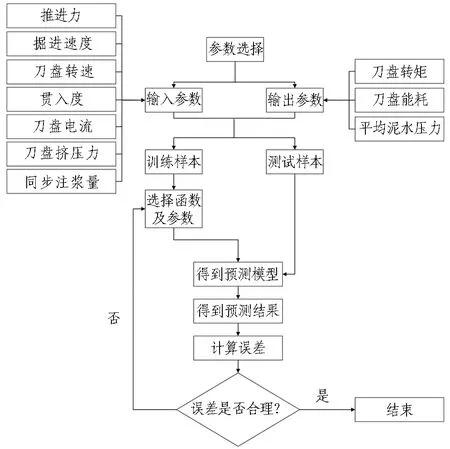
图3 预测模型算法流程图
为避免数据主观选择对预测结果造成误差,从选定的700环掘进数据中随机选取500组数据作为训练样本,其余200组数据作为测试样本验证预测模型精度。如图3所示,将500环数据中推进力等7个掘进参数值作为模型输入,将刀盘转矩等3个掘进参数值作为模型输出,展开训练,求出预测模型后,将其余200环数据中7个掘进参数值作为测试样本输入预测模型,对预测结果与实际结果进行误差对比。预测模型训练结果如表2和表3所示。
表2和表3分别示出预测模型训练过程中,各函数组合及不同隐含层神经元数目训练误差情况,通过对比可以确定训练误差最小为0.017 8时的函数组合,即输入层传递函数tansig、输出层传递函数tansig、训练函数trainbr、学习函数learngd,隐含层神经元数目11个。

表2 各函数组训练误差对比(部分)
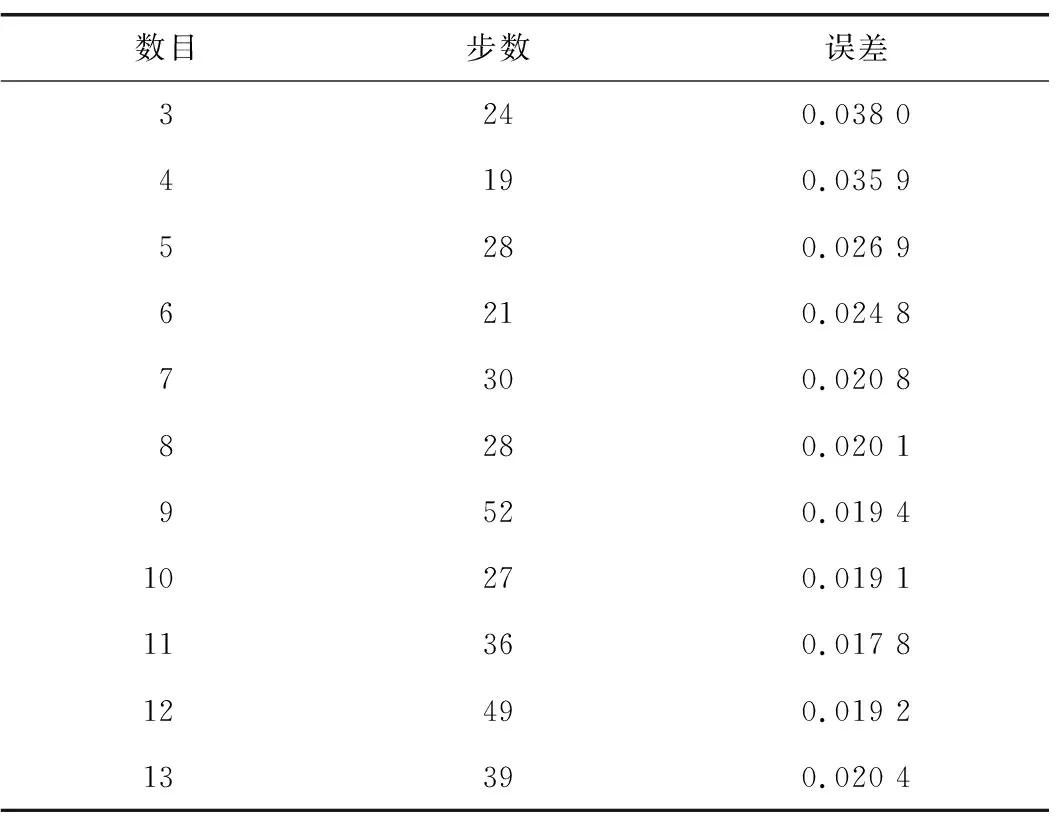
表3 隐含层神经元数目训练误差对比
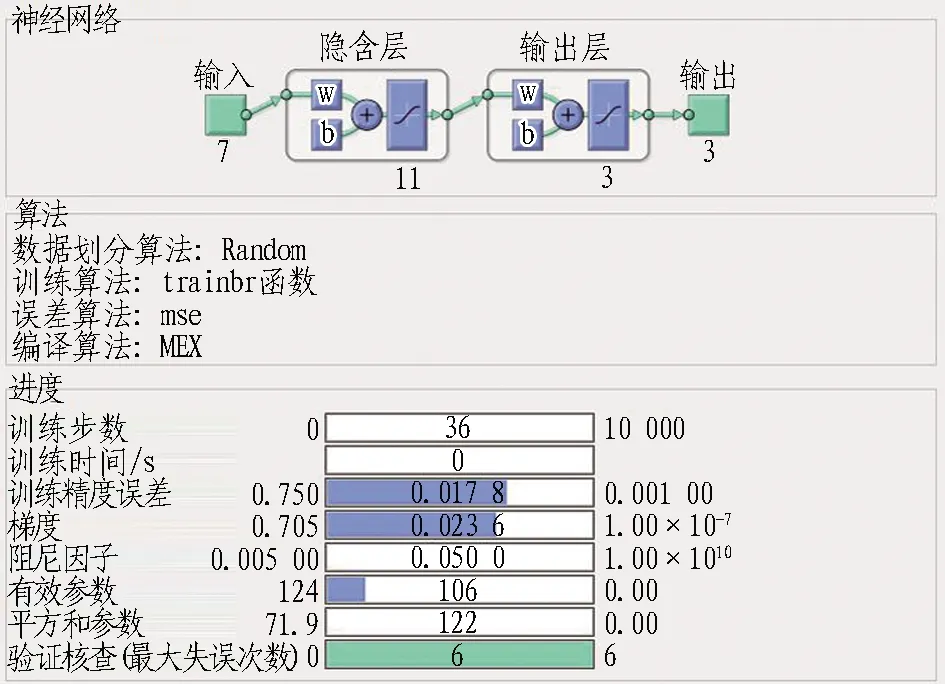
综上分析,最终确定神经网络预测模型结构为7-11-3,模型结构及训练结果如图4所示。
(a) 神经网络预测模型结构
由图4可知,当训练学习步数为36时,训练精度误差MSE达到最小值0.017 8,最大失误次数达到设定的6次,即误差曲线随着迭代次数增加而不再减小,因此停止训练。此时训练样本、测试样本以及总样本的多重相关系数分别为0.912 89、0.812 24和0.889 00,较接近于1,说明所选择的BP神经网络预测模型精度较高,预测样本输出结果和目标期望之间相关性较强,即选取结构为7-11-3的BP神经网络预测模型比较合理。
3.4 模型预测结果
3.4.1 复合地层预测结果
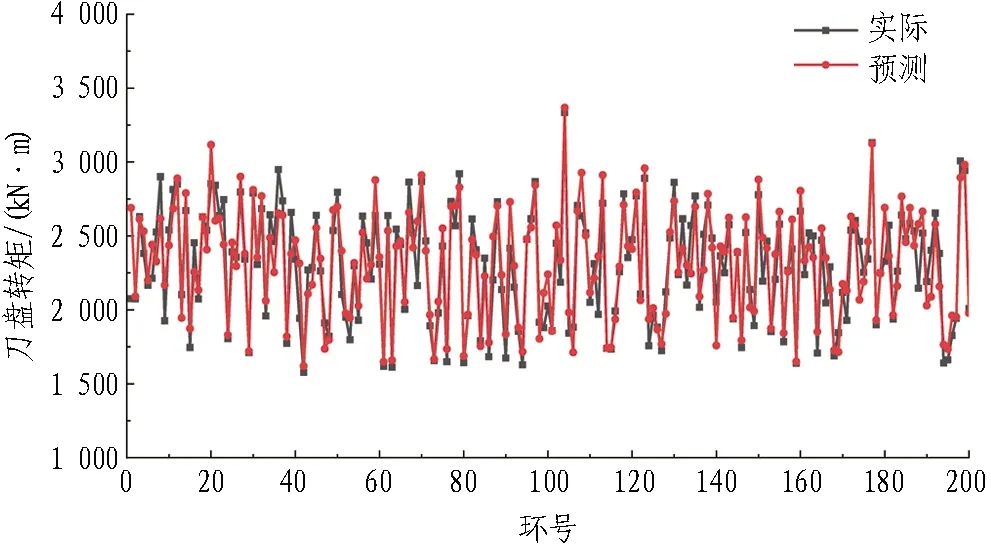
从复合地层选取的700环掘进数据中随机选取500环数据进行训练,其余200环数据进行预测,并对预测结果与实际结果进行相对误差分析,预测的掘进参数为刀盘转矩、刀盘能耗和平均泥水压力,预测结果和实际结果对比如图5和表4所示。
(a) 刀盘转矩
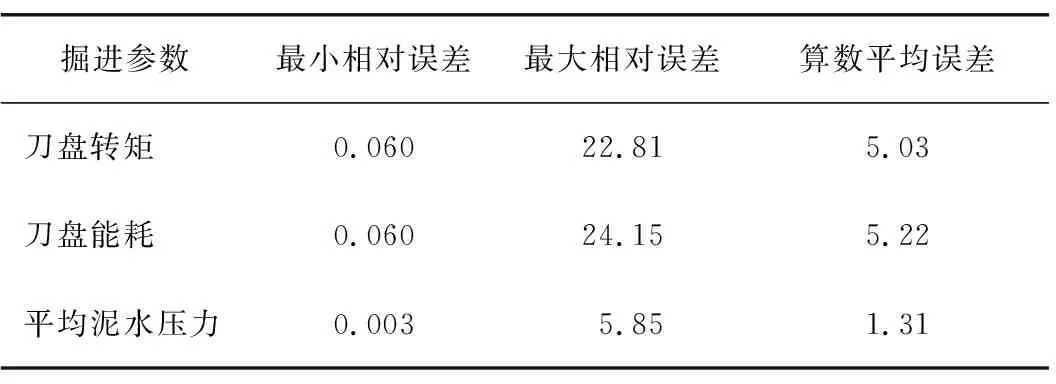
表4 复合地层刀盘转矩、能耗和平均泥水压力预测值与实际值的相对误差
由图5中预测值与实际值曲线的波动情况可看出预测效果良好。由表4可知,刀盘转矩和刀盘能耗预测值与实际值最小相对误差为0.06%,最大相对误差在23%左右,算数平均误差均在5%左右;平均泥水压力预测值与实际值最小相对误差为0.003%,最大相对误差为5.85%,算数平均误差为1.31%;预测精度较高,可满足盾构施工要求。
3.4.2 软土地层预测结果
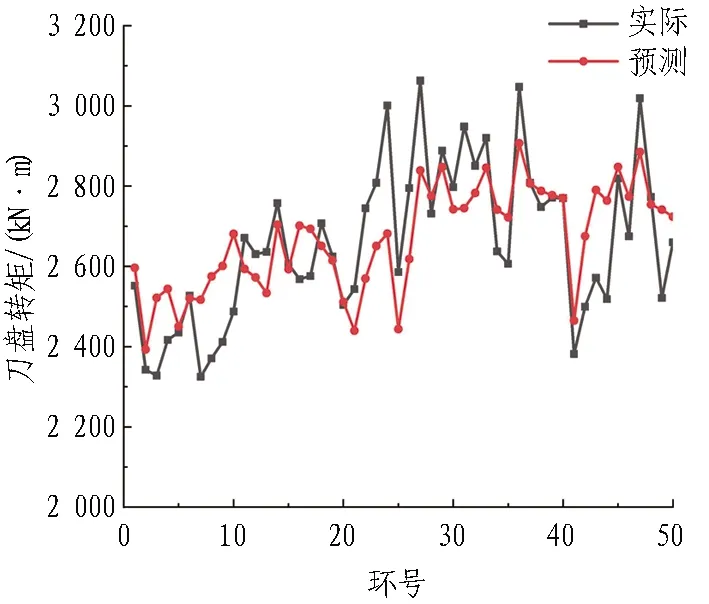
为进一步研究预测模型适用性及预测效果,重新选取复合地层中地质均匀的软土地层250环掘进数据,随机选取其中200环数据进行训练,其余50环数据进行预测,训练及预测步骤同复合地层,预测结果和实际结果对比如图6和表5所示。
(a) 刀盘转矩
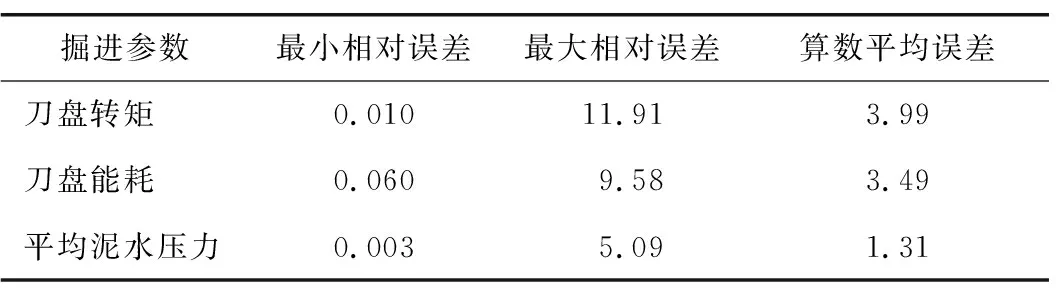
表5 软土地层刀盘转矩、能耗和平均泥水压力预测值与实际值的相对误差
由图6中预测值与实际值曲线的波动情况可看出预测效果良好。由表5可知,刀盘转矩和刀盘能耗预测值与实际值最小相对误差分别为0.01%和0.06%,最大相对误差在10%左右,算数平均误差在4%以内;平均泥水压力预测值与实际值最小相对误差为0.003%,最大相对误差为5.09%,算数平均误差为1.31%;相比于复合地层,预测精度进一步提高,基本满足盾构施工精度要求。
综上,由表4和表5看出,通过BP神经网络预测模型得到刀盘转矩、能耗和平均泥水压力预测值与实际值的算数平均误差在6%以内,基本满足盾构施工要求,但仍存在部分数据点预测值和实际值误差较大,经过分析,原因如下: 1)复合地层地质复杂,存在不明硬岩、孤石甚至是刀盘脱落的刀具,此时盾构各掘进参数出现突变,规律难以寻找; 2)盾构掘进参数的预测研究中,样本数据量越大则预测效果越好,本文研究的样本数据量为700环,数据量还不足够大; 3)研究对象是基于现场采集的掘进数据,该数据在采集过程中因设备等原因可能存在异常值,而后续数据清洗过程中无法完全清除异常值,因此产生一定误差; 4)本文研究的算法模型基于BP神经网络,该模型训练函数、网络结构、神经元个数、训练误差等都会对预测结果产生一定影响。
4 结论与讨论
针对汕头海湾隧道工程,本文建立基于BP神经网络的复合地层超大直径泥水盾构掘进参数预测模型,定量预测刀盘转矩、刀盘能耗和平均泥水压力,主要结论如下。
1)对复合地层700环掘进数据进行皮氏积矩相关系数分析,贯入度和掘进速度、贯入度和刀盘转速、刀盘电流和刀盘转速的皮氏积矩相关系数绝对值均在0.75以上,具有良好的线性相关性,而其他掘进参数之间的相关关系较不明确。
2)对复合地层700环掘进数据归一化处理,优选函数种类和网络结构构建基于BP神经网络的掘进参数预测模型,随机选取500环数据进行训练,其余200环数据进行预测,结果显示刀盘转矩和刀盘能耗预测值与实际值的算术平均误差在5%左右,平均泥水压力预测值与实际值的算术平均误差为1.31%,预测精度较高,基本满足盾构施工精度要求。选取软土地层250环掘进数据,随机选取200环数据进行训练,其余50环数据进行预测,结果显示刀盘转矩和刀盘能耗预测值与实际值的算术平均误差均小于4%,预测精度进一步提升。
3)当神经网络预测模型建立之后,只需要输入参数的值即可高精度定量预测出其他掘进参数,该过程依靠机器算法从而避免人为干扰。在实际掘进过程中,主司机可根据预测的掘进参数值与实际掘进参数值进行对比,偏差不大即可继续掘进; 当出现较大偏差时应停止掘进并上报分析数据,避免发生故障,经研究后调整相应的掘进参数以恢复掘进。此外,对于经验不足的主司机,可根据预测的掘进参数值进行调整,以达到安全掘进的目的。
目前对于盾构掘进参数的研究,较少涉及超大直径泥水盾构及复合地层,且掘进参数预测较为单一。本文实现了复合地层超大直径泥水盾构掘进参数多输入多输出预测,同时对刀盘能耗及平均泥水压力进行了探索。今后可进一步改进之处: 解决BP神经网络存在局部极小点和不收敛问题,研究更加合理的算法模型以提高预测精度和效率; 探索异常数据点与正常数据点之间的关系; 本文研究了复合地层环与环之间的掘进参数预测,可进一步实现以时间为纽带的掘进参数实时预测和地层预测,以更好地达到智能掘进的目的。

