基于模糊C均值聚类算法的碳纤维木质复合材料图像分割

何 栋，唐 婷

（西安航空职业技术学院， 陕西西安 710089）

相比于普通人造板而言，新型的碳纤维木质复合材料无论是在电学性能还是力学性能上都有着大幅的提升，因此木质复合材料的应用效果也更为良好。通过图像分割的方式可明确碳纤维特征参数，根据所得结果分析该材料的宏观性能，兼具宏微观研究的双重效果，是有效分析碳纤维木质复合材料性能的关键，在工艺优化方式上也具有重要的参考价值。

1 FCM 分割算法

FCM 分割算法的特点在于计算便捷，可省去训练样本。依托于像素邻域信息，可获得改进FCM 算法，在成分信息丰富、形态组成类别多的树木图像中可达到有效分割的效果。需明确的是，上述方法只是发挥出了像素自身的特征价值，而缺乏对像素的邻域信息与局部作用之间的关联性分析，存在噪声干扰问题，同时分割边缘较为模糊。基于上述问题，本文在FCM 算法基础上引入了小波变换的方式，充分发挥出二者的优势，最终分割效果良好，同时运算效率大幅提升。

2 碳纤维木质复合板电镜图像增强

电镜图形放大倍数设定为500，共选取150 幅图像，各自的大小保持一致，均为1024×943。电镜图像较为复杂，存在大量不定型胶、木纤维的形态也表现出差异化的特点，若要有效提取碳纤维的特征并非易事，图像增强是实现有效分割的关键前提。经过图像增强操作后，其分辨力有所提升，可有效呈现碳纤维信息，并且淡化以木纤维为代表的无价值信息，达到消除噪声影响的效果。本文根据图像增强的技术特点，获得直方图，并将其与电镜下的原始图像对比分析，具体如图1 所示。

图1 原始图像及灰度直方图Fig.1 Original image and gray histogram

根据图1 内容得知，灰度值得到有效的扩展，由原本的[40,255] 变更为[0,255]，实现在对比度上的提升，再通过直方图均衡的方式，更为清晰地突出碳纤维，具体如图2 所示。通过图像平滑的方式，中值滤波具备有效抑制噪点的能力，根据本电镜图像的特点，使用到的是3×3、5×5、7×7 模块，在其作用下实现中值滤波，结果表明7×7 模板的应用效果最为良好。经上述处理后，图像品质大幅提升，分辨率与识别能力优良，各处细节更为清晰，可为后续的图像分割工作创造良好条件。

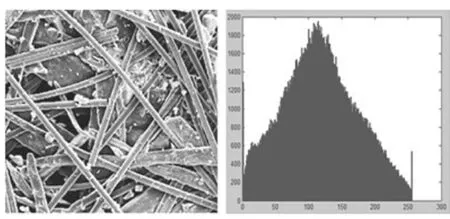
图2 均衡化后的图像及灰度直方图Fig.2 Image and gray histogram after equalization

3 基于小波变换的改进FCM 图像分割算法

3.1 FCM 基本理论

FCM 算法运行中，在最小化目标函数的支持下，可达到样本最优划分的效果，汇总n 个样本并将其聚成c 类。给出目标函数表达式，具体如下：

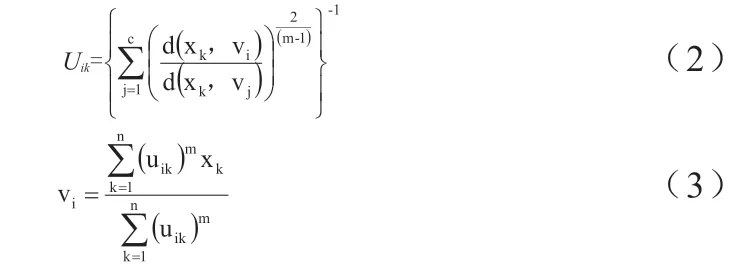
3.2 新改进 FCM 算法

从小波分析的应用特点来看，噪声并不会对低频图像带来过多的影响，且发挥出全局信息的优势。由于小波系数在具备尺度内聚类特点的同时还兼具尺度间持久性，因此除了要考虑低频分量灰度值外，还要结合领域小波系数做综合性分析。低频图像中引入FCM 算法后，可得到初始分割结果，并明确聚类中心，在此基础上以聚类结果为准，给予各分类相对应的标签，换言之，各像素都被赋予特定且独立的标签。在小波图像重构时，可获得所有小波系数特点标签，遵循的是由低频至高频的原则，同时还可获得图像的聚类中心。

小波初始分割时并未使用到各层的高频系数，从这一角度来看，图像重构后将出现细节信息不完整的问题。依托于重构图像的信息，发挥出邻域像素灰度值的优势，将其引入至改进的FCM 算法中，从而完成对原图像的分割处理。在产生的小波重构图像中，各像素都被赋予特定的小波系数标签，若出现标签相一致的情况，所对应的灰度值则相同，表明二者间产生的欧氏距离有所减小，根据此特点，为之定义一个参数，通过此方式可达到如下效果：编号相同时欧式距离缩小，反之则加大[2]。

式（4）中的 g 值范围为：0＜g＜1。使用改进 FCM算法时，若输入图像未发生变化，并且其他参数也保持一致，此时g 值分别取0.5、0.6、0.7、0.8、0.9。综合对比各实验结果，得知g 的取值以0.8 最为合适，此时图像分割效果优良。鉴于此，重新定义像素灰度值xk与v1的距离，具体有：

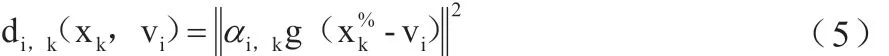
在FCM 算法运行过程中，仅考虑的是像素的灰度值，而未顾及到邻域像素的信息。根据此特点，再次定义像素的特征值，具体关系为：

式（6）中：xk为像素的灰度值；NR为邻域像素的个数；N（xk）为像素的邻域像素；为邻域像素的平均灰度；β (0≤β ≤1) 为权重因子，此指标可反映像素与邻域像素所产生的相似性程度，伴随该值的提升，相似度也随之加大：

式（7）中:Sk,j为像素xk与其邻域像素xj相似系数。给出该指标的定义：

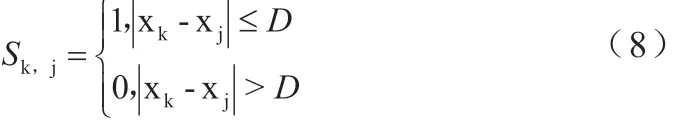
式（8）中：D 为预定义的阈值，结合碳纤维木质复合材料的特点，最终将D 值取为5。

4 基于小波变换与FCM 算法的图像分割

根据图像处理要求，选择的是MATLAB2014a 软件。遵循如下流程完成图像处理工作：Step1：处理原始图像；Step 2：执行小波分解与重构操作，引入FCM算法，通过对低频图像的分析后确定聚类中心与初始标号；Step3：根据式（6）计算，可求得像素的特征值；Step4：根据式（5）展开计算，获得像素至聚类中心的距离；Step5：综合使用式（2）与（3），分别确定隶属度和聚类中心；Step6：在式（1）的支持下，可求得目标函数J；Step7：综合对比两次目标函数，若满足( 也可采取T＞Tmax的判别标准)，此时应聚类停止，结束所有的分割作业，若不满足该要求则要退回至Step3，遵循上述提及的流程再次执行。确定本算法的参数值，具体为：权重因子m=2，聚类数c=4，迭代误差ε最小值为0.00001，最大值为100。经综合分析后得知，在传统FCM 算法中，存在不具备空间约束力的问题，若将其引入图像分割工作中，则会出现大量的误分割现象，产生的碳纤维区域不够清晰，并分布有较明显的噪声斑点[3]。相比之下，改进的FCM 算法则更具可行性，可清晰区分碳纤维与木质纤维，能够更准确地突出碳纤维区，有效抵御噪声的不良影响，具备优良的分隔效果。而通过电镜图像实验，整理各方法的迭代次数与运行时间，具体内容见表1。

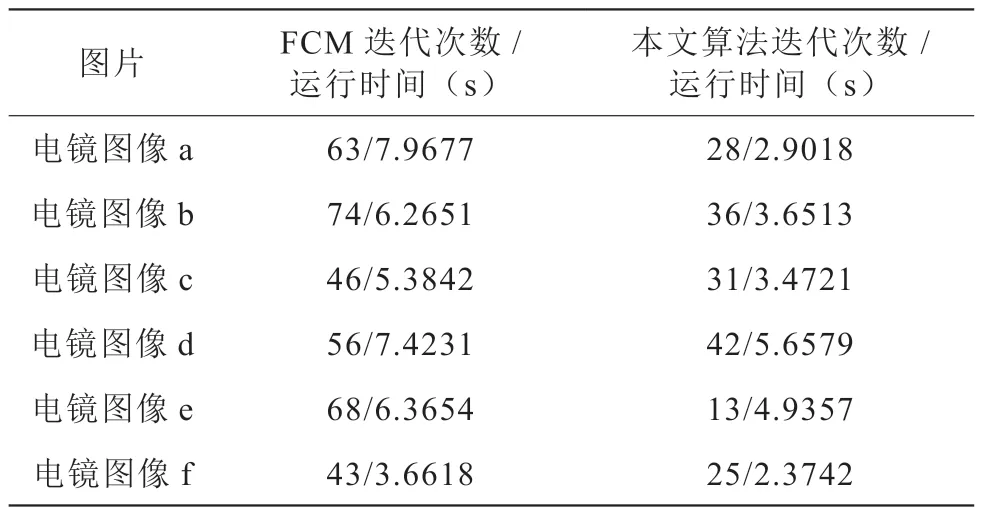
表1 两种算法的迭代次数与运行时间对比Table 1 Comparison of the number of iterations and running time of the two algorithms

根据表1 的数据得知，无论是迭代次数还是运行时间，相比于常规方法而言，本文所选择的改进FCM 算法在两项指标上都表现出减小的趋势，即迭代次数缩减的同时运算效率大幅度提升。

5 结语

基于碳纤维木质复合材料的结构特点，其电镜图像表现出材料组成复杂、形态多样化的特点，有用信息的提取难度相对较大。若要为碳纤维特征参数提取工作提供可靠的指导，就必须有效分割碳纤维。本文中，通过对图像的预处理后，所得的电镜图像的清晰度随之提升，是图像分割的重要准备工作。而实际图像分割过程中，则结合低频图像分割结果与邻域像素信息，获得经改进后的FCM 算法，提出了具有可行性的欧式距离计算函数，并在既有的像素特征值计算途径基础上做出优化，有效解决了分割误差大、噪声敏感、边缘聚类等不良问题，缩减迭代次数，从而有效提升了算法运行效率，总体上具有较好的可行性。