江坪河水电站导流洞衬砌失效条件下涌水量计算及预测分析

龚亚琦，苏海东，李家正

(1.长江科学院材料与结构研究所，湖北 武汉 430010；2.水利部水工程安全与病害防治工程技术研究中心，湖北 武汉 430010)

0 引 言

江坪河水电站位于高山峡谷区，河床狭窄，汛期洪水峰高量大，洪枯水位变幅大，采用一次拦断河床的隧洞导流方式。导流隧洞位于右岸，闸门控制段上游为压力隧洞段，圆型断面，直径7.00 m，闸门控制段后接无压隧洞，断面为城门洞形，断面7.00 m×11.45 m(宽×高)。施工期间，闸门后渐变段桩号D0+382下游渐变段顶拱开挖为平面时，因没有及时进行临时支护造成顶拱塌方，塌方区域可能延伸到桩号D0+400左右，呈上游高下游低的阶梯形状，最大空腔高度3.48 m。该部位于后期分两次进行了混凝土开挖回填，回填桩号为D0+382～D0+402。针对上述情况，考虑到后续塌方的可能性，设计方制定了衬砌极端失效情况下的应急抢险预案以保障下闸蓄水安全，其中最大涌水量的测算是应急抢险预案设计的关键问题。

1 隧洞涌水量预测研究方法

隧道涌水量的预测涉及到隧洞渗流场计算，目前主要的计算方法包括解析方法和数值模拟方法。

解析方法基于一定的假设，推导简化的涌水量解析公式，解析解公式简洁、概念清晰，可快速估算衬砌涌水量和外水压力，非常适合应急抢险预案设计时进行相关参数的敏感性分析[1]，受到国内学者的关注。2004年，王秀英等[2]根据地下水动力学理论，以无限含水层中的竖井为例，将圆形隧洞渗流场求解简化为轴对称问题，推导了山区高水位隧道排水量及衬砌、注浆圈水压力的解析公式，并应用于圆梁山隧道涌水量预测。2012年，李鹏飞等[3]采用相同的思路，推导了类似的渗水量解析公式，并对厦门海底隧道渗流场进行了研究。2011年，童磊等[4]利用复变函数方法，推导了考虑衬砌排水特性的半无限空间隧洞渗流量的解析表达式。2018年，潘以恒等[1]推导出半无限平面含注浆圈深埋隧洞渗流场解析解。王帅等[5]采用镜像法推导了半无限平面平行3孔海底隧道渗流场解析式。数值模拟方法根据水文地质资料，模拟实际边界条件建立数值模型，通过求解渗流场，预测涌水量。2015年，杨文亮[6]分别采用解析法和有限元法对胶州湾隧洞涌水量进行了预测，讨论了注浆圈厚度和渗透系数参数的选取。2017年，崔少东等[7]将非饱和渗流引入到地下洞室涌水量计算中，分析了最大涌水量随时间的变化规律。

总的来看，目前隧洞渗流场解析方法研究已经逐步发展为可综合考虑围岩、注浆加固圈、初期支护和二次衬砌的整体渗流模型。但是，解析公式主要基于圆形隧洞断面假设且围岩为各向同性[6]，在工程中有一定的局限性。渗流场数值模拟方法可以模拟实际地质条件，预测各向异性和不同断面隧洞的涌水量，但是计算量大，操作复杂。

本文基于江坪河导流隧洞闸门后渐变段的矩形断面型式，分别采用解析方法和有限元数值方法计算导流洞的涌水量，验证解析方法求解矩形断面问题的适用性，并开展敏感性分析，为应急抢险预案设计提供理论支撑。

2 圆形断面隧洞涌水量计算解析公式

圆形断面隧洞(见图1)模型参数如下：隧洞半径为ra，承受内水水头ha；二次衬砌外半径为r2，外侧水头为h2；初期支护外半径为r1，外侧水头为h1；灌浆加固半径为rg，外侧水头为hg。

假设隧洞衬砌及周围围岩均为均质体，且材料的渗透系数在各个方向相同，渗流方向以径向为主。假定半径r0以外形成的稳定渗流场水头与隧洞中心点静水压力水头h0相等。基于上述假设，可将隧洞地下水渗流场分布按轴对称平面应变问题求解。文献[3]推导的圆形隧洞的渗水量Q的解析公式

(1)

式中，ks、k2、k1、kg分别为隧洞、二次衬砌、初期支护和注浆加固圈的渗透系数；ra、r2、r1、rg、r0隧洞半径、二次衬砌外半径、初期支护外半径、灌浆加固半径和围岩半径；ha为隧洞承受内水水头。将式(1)右侧分母经过对数变化，可以转为文献[2]给出的涌水量解析公式。

令n2=ks/k2，n1=ks/k1，ng=ks/kg

则式(1)可以表述为

(2)

图1 隧洞地下水渗流场计算模型

3 毛洞涌水量解析解与数值解验证

3.1 涌水量解析解模型

江坪河导流洞闸门后渐变段洞室的开挖面积约为203 m2。为了应用解析公式，首先将矩形断面采用面积等效近似为隧洞内半径ra=8.04 m的圆形洞室。

根据式(1)，不考虑内水压力，ha=0，初期支护外等效半径r1=8.20 m(喷射混凝土厚度约0.12 m)，隧洞中心高程为300.00 m，根据模型假定，r0=h0=130 m(水头按430.00 m考虑)。

3.2 有限元渗流场模型

根据江坪河导流洞闸门后渐变段洞室矩形断面建立二维有限元模型，进行渗流场分析。洞室混凝土为25 m×21 m(宽×高)的矩形孔，整个计算模型尺寸为225 m×225 m，围岩按∈2g考虑，渗透系数ks=1.2×10-6m/s，有限元模型如图2所示。

图2 二维有限元渗流场分析模型

将有限元模型计算的涌水量与理论模型的毛洞结果进行比较，如表1所示。从表1可以看出，有限元模型和理论模型计算的涌水量数值比较接近，说明采用面积等效后，解析方法的涌水量预测值可靠。

表1 毛洞断面涌水量计算结果

4 极端失效条件下导流洞涌水量预测

假设导流洞衬砌发生极端失效条件，针对式(2)中，n2=0，不考虑灌浆，则ng=1。渗透系数是决定水下隧道涌水量的最主要因素[6]，下面对比不同渗透参数条件下导流洞的涌水量。图3为不同围岩和初期支护渗透系数比值n1条件下，涌水量的预测值。

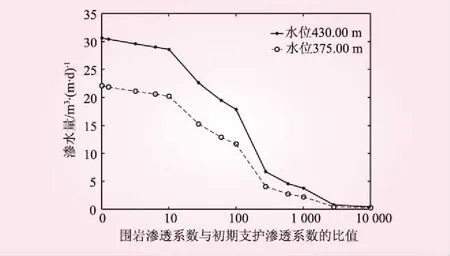
图3 不同围岩渗透系数/初期支护渗透系数比例下涌水量

由图3可知，不考虑灌浆且围岩渗透系数一定的条件下，涌水量随着初期支护渗透系数的降低而不断减小。具体来看：当n1=1，即初期支护渗透系数(k1=1.2×10-6m/s)与围岩渗透系数相等时，430.00 m水位和375.00 m水位涌水量分别约为30.43 m3/(m·d)和21.88 m3/(m·d)；当n1=100，即初期支护渗透系数(k1=1.2×10-8m/s)时，430m水位和375.00 m水位涌水量分别约为17.89 m3/(m·d)和11.68 m3/(m·d)；当n1=500，即初期支护渗透系数(k1=2.4×10-9m/s)时，430.00 m水位和375.00 m水位涌水量分别约为6.71 m3/(m·d)和4.05 m3/(m·d)；当n1=1 000，即初期支护渗透系数(k1=1.2×10-9m/s)时，430.00 m水位和375.00 m水位涌水量分别为3.77 m3/(m·d)和2.23 m3/(m·d)。

5 结 论

(1)假设江坪河导流洞原塌方段发生衬砌失效的极端情况，本文分别采用解析方法和有限元数值方法预测导流洞的涌水量。涌水量结果表明，解析方法在满足假设条件下有很好的适用性。

(2)根据涌水量解析法，在不考虑灌浆且围岩渗透系数一定的条件下，涌水量随着初期支护渗透系数的降低而不断减小。不同渗透参数条件下最大涌水量预测，可为应急抢险设计提供参考依据。