基于Prophet模型的江坪河水电站面板堆石坝变形预测

冷天培，马 刚，殷彦高，谭 瀛，周 伟

(1.武汉大学水资源与水电工程国家重点实验室，湖北 武汉 430072；2.中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014)

0 引 言

混凝土面板堆石坝以其工程造价低、施工简便、对地形地质适应性强等优点，在水电建设中占据了越来越大的比重，成为当今最热门的坝型之一。随着筑坝技术的不断发展[1]，面板堆石坝呈现坝体高度不断增加，工程规模不断扩大的趋势，给堆石坝变形控制带来不小的挑战。变形控制重要环节包括变形监测和变形预测，变形监测便于掌握大坝当前的工作性态，而变形预测为工作性态评估和进一步的变形调控提供数据支撑。

目前，用于堆石坝变形预测和工作性态评估的方法主要有有限元模拟[2]、统计模型[3]、灰色理论[4-5]、人工神经网络[6]、时间序列模型[7]等。其中，有限元模拟应用最为广泛，但其对于堆石体本构模型和与之匹配的模型参数依赖性较强，且实施过程中需要人工干预的环节较多，成本较高，不便于快速部署进行实时预测。统计回归模型采用影响因素与变形之间的回归关系对大坝进行变形预测分析，变形与影响因素之间并不遵守简单的统计回归，具有一定的局限性。针对数据资料不完整、考虑因素不全面而产生的灰色特性，以及各影响因素与坝体变形之间存在的模糊特性，学者们常用灰色理论模型和自适应模糊推理系统[8-10]预测变形。人工神经网络具有强大的自学习和修正误差能力，在理论上能逼近任何非线性系统，为大坝安全监控提供了一条有效的思路和方法，但该算法存在可能收敛到局部极小和系统训练不稳定的弱点。此外，支持向量机[11]及改进M5′-主成分模型树[12]等机器学习方法也被运用于堆石坝变形预测，与传统预测模型相比，这些机器学习方法能较好地反映影响因素与变形之间的非线性关系，能够有效提高变形预测精度[13]。

机器学习中的Prophet模型能有效分析时间序列的周期性及趋势性，同时考虑误差等因素的影响，且其参数具有可解释性，可根据需要方便调整，在大坝变形预测方面具有可行性。为此，本文依托江坪河水电站面板堆石坝，在对实际监测数据进行分析的基础上，采用Prophet模型进行大坝变形预测分析，检验Prophet模型对大坝变形的预测精度。

1 基本理论

1.1 Prophet预测模型

Prophet模型将时间序列分为4部分，即

y(t)=g(t)+s(t)+h(t)+εt

(1)

式中，y(t)为时间序列数据；g(t)为趋势项，表示时间序列在非周期上面的变化趋势；s(t)为周期项，表示时间序列在一定时间内的周期变化；h(t)为节假日项，表示节假日的影响(在大坝变形预测中一般用不上)；εt为误差项，表示可能存在的各种误差。

趋势项模型g(t)在Prophet算法中分为2种函数：一种是逻辑回归函数，即逐渐趋近于某一数值，公式如下

(2)

式中，C(t)为最大容量，随时间变化而变化，需要人为提前设置；k+α(t)tδ为增长率，其值越大，增长速度就越快，越容易达到最大容量；m+α(t)Tγ为偏移量。g(t)的另外一种函数为分段线性函数，即趋势随时间变化而变化，公式如下

g(t)=(k+α(t)δ)·t+(m+α(t)Tγ)

(3)

周期项s(t)采用傅里叶级数来拟合，假设P作为时间序列的周期，其傅里叶级数的形式为

(4)

式中，an和bn为傅里叶系数；t为时间。

1.2 贝叶斯优化

大部分时序预测模型都有很多超参数需要人为设置和调整，贝叶斯优化能利用先验知识高效地调节超参数。相对于其他自动调参方式，贝叶斯调参迭代次数少，效率高，对非凸问题依然有效。

1.2.1高斯过程

贝叶斯优化基于高斯过程，高斯过程是随机过程的一种，是一系列服从高斯分布的随机变量在一指数集内的组合。高斯过程中任意随机变量的线性组合都服从多维高斯分布，可通过使用无限维多变量高斯分布来对未知函数进行建模。对于所有x=[x1，x2，…，xn]，f表示高斯过程，即

f(x)～N(μ(x)，K(x，x))

(5)

式中，μ(x)表示均值函数，返回各个维度的均值；K(x，x)为核函数，核函数在高斯过程中生成1个协方差矩阵来衡量任意2点之间的距离。

高斯过程的先验分布写为f(x)～N(μf，Kff)，在观察到一组数据点(x*，y*)后，假设y*与f(x)服从联合高斯分布，即

(6)

基于先验和一定的假设(联合高斯分布)计算得到高斯过程后验分布及其均值函数和协方差矩阵，即

(7)

1.2.2采集函数

通过高斯过程对目标函数建模，贝叶斯优化就可以在超参数空间中抽取超参数组合评估模型的性能。为避免陷入局部最优，贝叶斯优化需要在探测(未取样区域，高方差)和开发(后验分布的最优解附近，高均值)之间找到一个平衡点。根据高斯分布的样本均值和方差这2个统计量，定义合适的采集函数，使下一次采样在开发和探索之间权衡。常用的采集函数UCB为

UCB(x)=μ(x)+βσ(x)

(8)

式中，σ(x)表示方差函数；β表示均值与方差之间的权重关系，反映了在开发与探索之间的权衡。

2 江坪河水电站大坝监测资料分析

2.1 仪器布置

江坪河水电站工程安全监测设备是根据坝址的地形地质条件、混凝土面板堆石坝结构和施工特点等进行设计布置的，主要是为了解大坝填筑施工期及运行期坝基、坝体的变形和渗流情况，并掌握相应时期坝基、坝体的变形和渗流的规律，以利于现场施工质量控制，并为判断大坝结构安全提供依据。

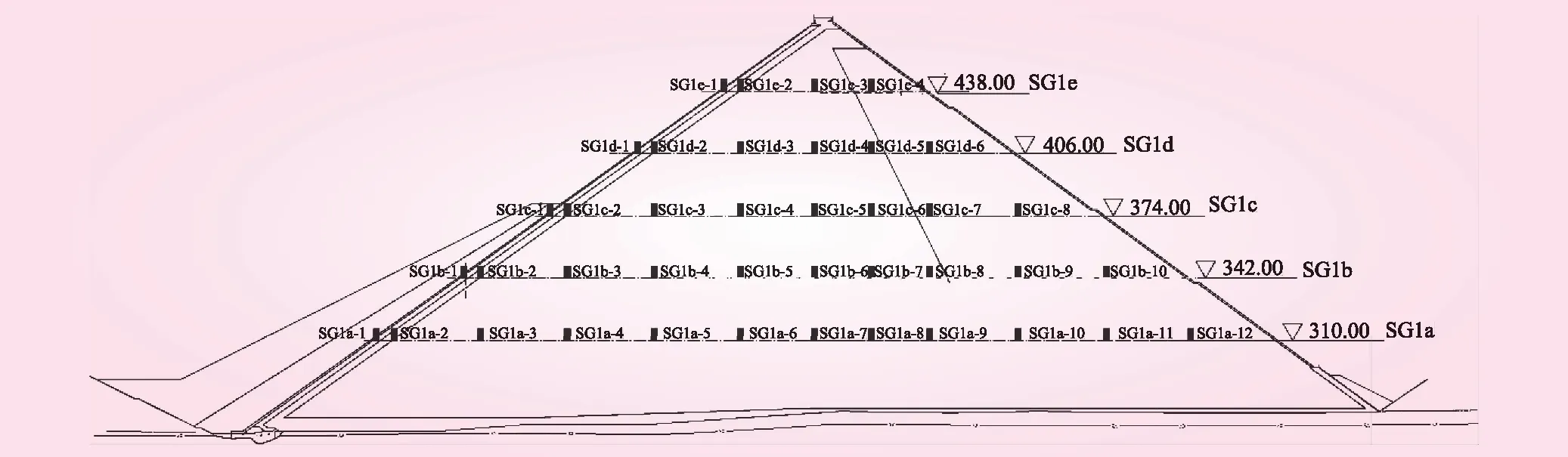
图1 大坝L0+010.000断面监测点布置(高程：m)

坝体沉降监测以坝L0+010.000、坝L0+060.000和坝R0+050.000这3个监测断面为代表，共布设11条测线，73个测点，采用水管式沉降仪监测坝体沉降。坝L0+010.000观测剖面在5个高程上(310、342、374、406 m和438 m)布置了沉降仪40组；坝L0+060.00观测剖面在3个高程上(374、406 m和438 m)布置了沉降仪15组；坝R0+050.000观测剖面在3个高程上(374、406 m和438 m)布置了沉降仪18组。大坝L0+010.000观测剖面变形监测仪器布置见图1。

在水管式沉降仪对应高程的堆石坝体下游面引出端修建观测房，所有仪器电缆就近引入观测房内集中采集监测数据。整个安全监测仪器埋设施工紧密结合坝体填筑、面板混凝土浇筑及相应土建施工进度进行。仪器埋设安装后，即根据设计要求进行监测数据采集。

2.2 垂直位移

堆石坝的沉降主要是由堆石料的压缩变形产生的。堆石料的压缩变形，初期主要是颗粒的位移与结构调整，并伴有少量的颗粒棱角破碎，这是变形较快的主压缩阶段；其后，随着颗粒破碎的增加，将进入次压缩阶段，变形趋于平稳。通过整理江坪河水电站面板坝坝体沉降的实测资料，得到坝L0+010.000断面分别位于310、342、374、406 m和438 m高程的测点沉降过程线，见图2。从图2可知：

(1)310 m高程水管式沉降仪前期各测点沉降测值随填筑高程的升高发展较快，后期随时间基本平稳发展。2015年各测点测值均出现较小波动，可能为大坝重新施工所致，随后各测点测值随时间稳定发展。

(2)342 m高程水管式沉降仪大部分时段平稳发展。2015年复工阶段，各测点测值出现波动，之后恢复正常稳定发展。

(3)374 m高程水管式沉降仪绝大多数测点测值随时间平稳发展。SG1c- 02号测点在2017年9月出现了30 mm的波动起伏，这可能与仪器安装初期进行调试工作有关，SG1c- 02号仪器在2017年10月以后测值平稳发展，与其他测点规律性一致。SG1c- 05、SG1c- 06和SG1c- 07测点在2018年4月30日后无监测数据，仪器可能损坏。

(4)406 m高程水管式沉降仪各测点测值随时间逐渐发展，在绝大部分时间内发展平稳。SG1d- 01号测点在2018年5月25日出现了约30 mm的波动，SG1d- 04号测点测值在2018年4月3日出现约20 mm的波动，SG1d- 06号测点测值在2018年4月3日出现约35 mm的波动，但随后均恢复到原趋势线水平，可能是调试仪器所致。

(5)438 m高程各水管式沉降仪的测值随时间平稳发展，除SG1e- 01号测点在2018年7月10日产生约10 mm的波动外，没有产生其他突变或损坏现象，说明仪器工作正常。

3 大坝变形预测

3.1 数据预处理

本文选取江坪河水电站面板堆石坝L0+010.000断面SG1a- 01～SG1a-12测点的监测资料，并对监测数据进行自相关性检测，见图3。图3中，1个滞后期代表1个月。从图3可以看出，在滞后期小的数据之间的自相关性很高，随着滞后期变大，数据之间的自相关性也随之减弱，呈现出短期相关关系。且自相关系数没有逐渐趋近于0，说明监测数据是非平稳序列[14]，这也说明了监测数据存在趋势性。而Prophet模型可以直接对非平稳时间序列进行预测，不用进行平稳化处理。

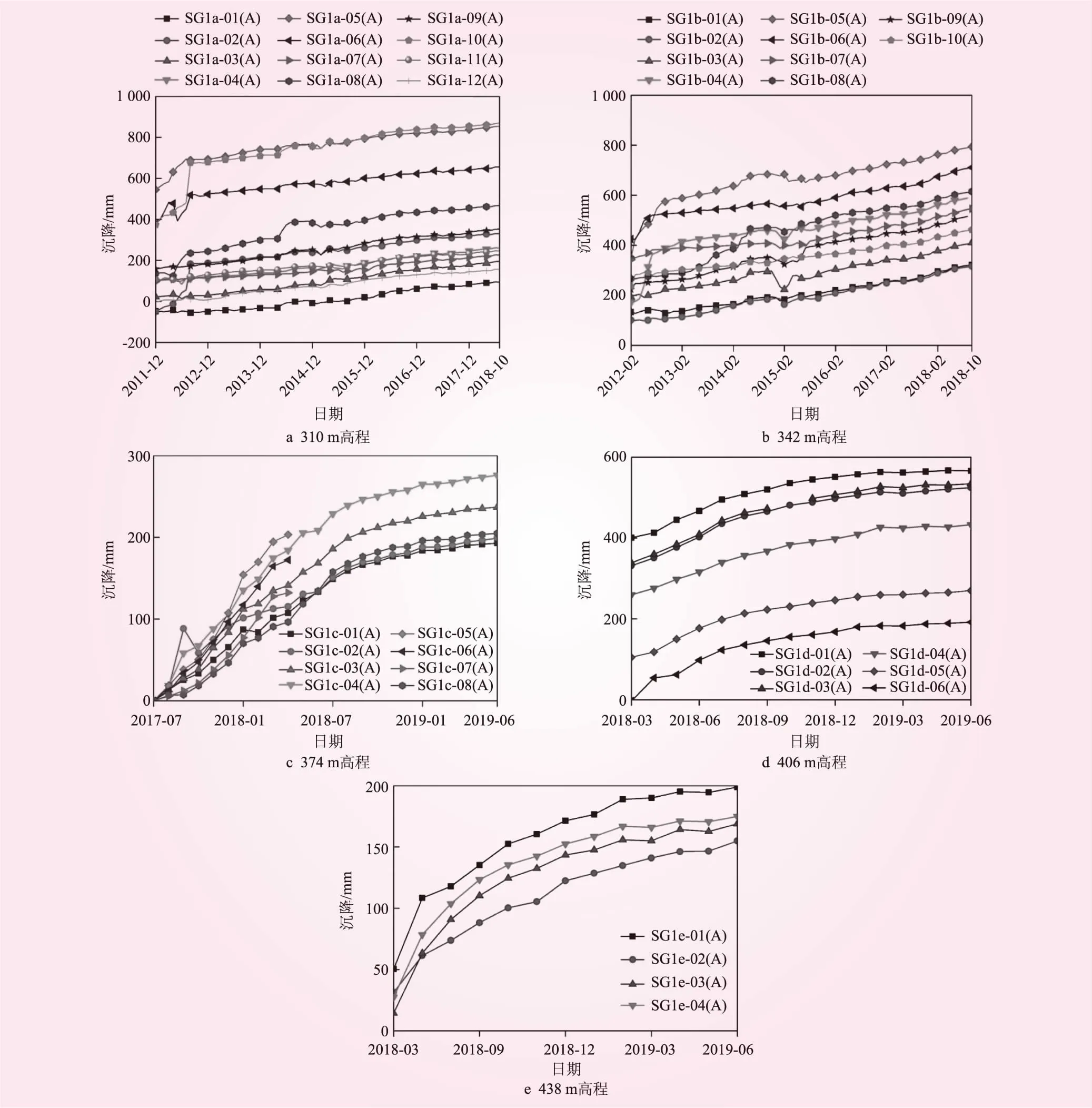
图2 垂直位移过程线

将2011年4月10日～2018年8月7日的变形监测数据作为原始样本，其中2011年4月～2017年7月的监测数据作为训练集，2017年8月～2018年2月的监测数据作为评估集评估模型超参数优劣，2018年2月～2018年8月的监测数据作为测试集测试模型预测精度。

3.2 Prophet预测大坝变形

本文采用Prophet模型，预测江坪河水电站面板堆石坝的大坝变形。输入训练集训练模型，并将结果与评估集比较确定模型超参数优劣，然后运用贝叶斯优化过程不断重复上述操作，最终得到最适合的超参数组合，最后将训练集和评估集输入贝叶斯优化后的模型进行预测。预测流程见图4。

3.3 预测结果分析

运用上述步骤对大坝变形进行预测，并将预测结果与测试集相比较。为更直观地表现预测效果，图5给出了同一时刻SG1a- 01～SG1a-12的预测误差。图5中，点越靠近y=x这条线说明这一时刻该测点的预测值与实际值越接近，即预测误差越小。从图5可以看出，在各时刻下各测点的预测值与实际值均没有较大的差别，表明模型预测效果良好。图6给出了SG1a-12的预测结果。从图6可以看出，预测值与测试集结果接近，进一步验证了Prophet模型的预测效果。

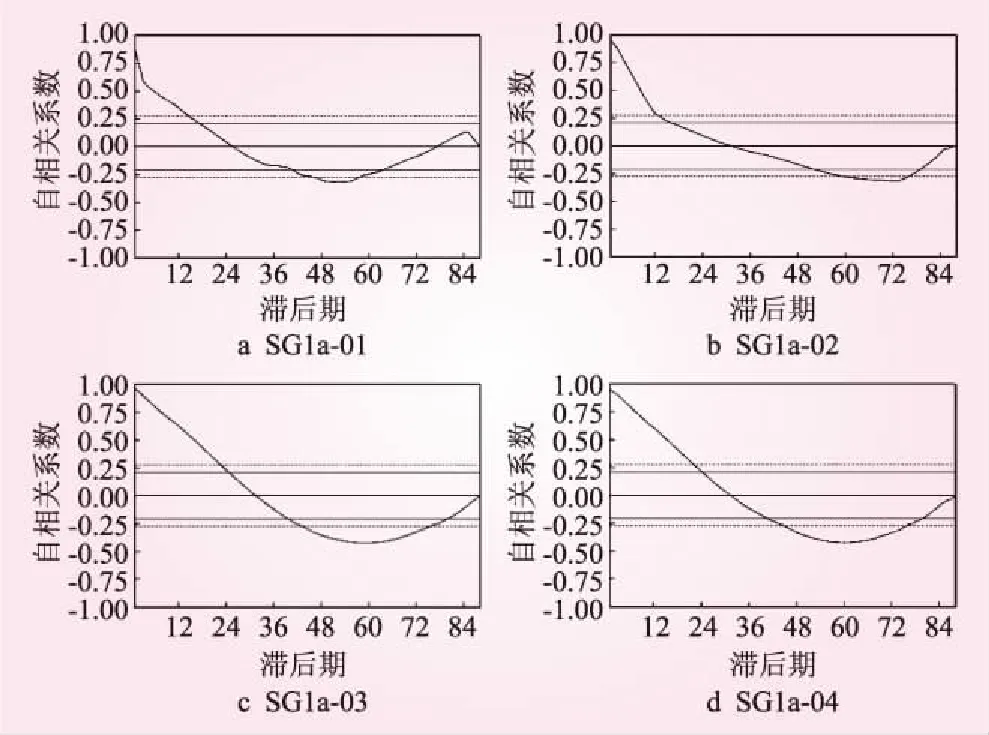
图3 监测数据自相关性检测

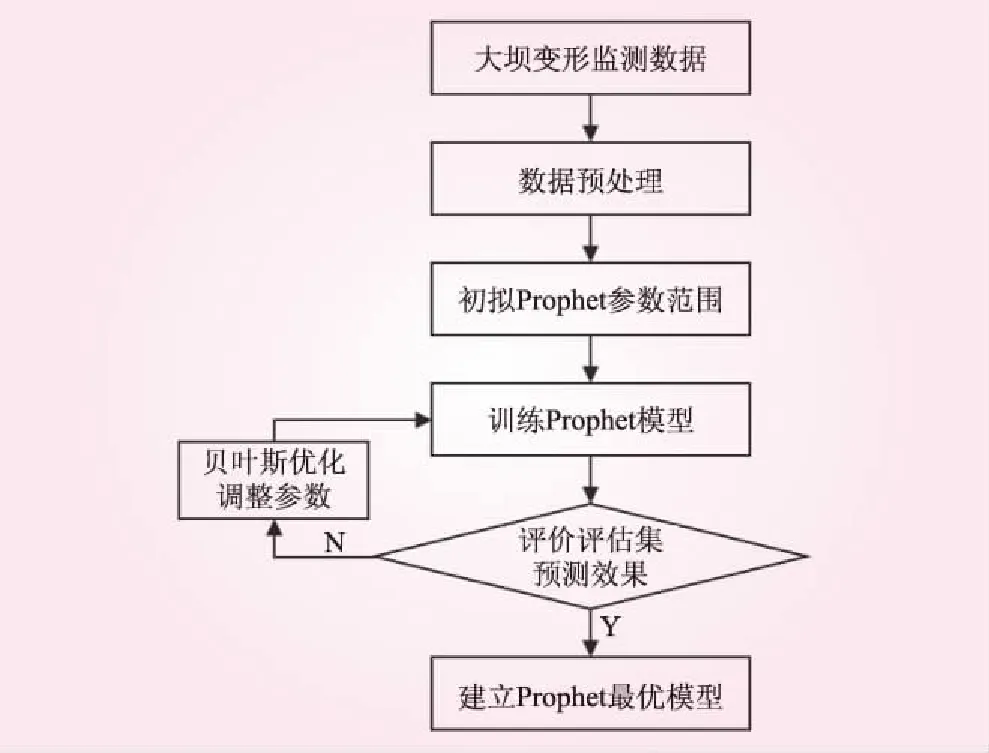
图4 大坝变形预测步骤

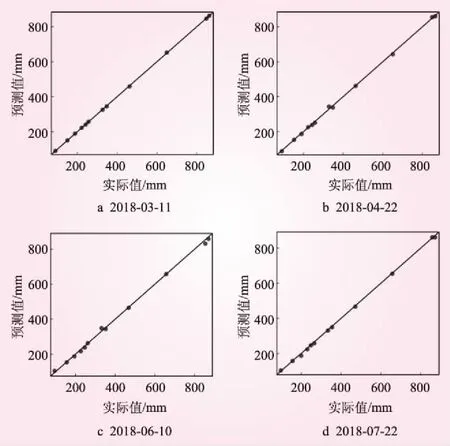
图5 同一时刻各测点预测误差

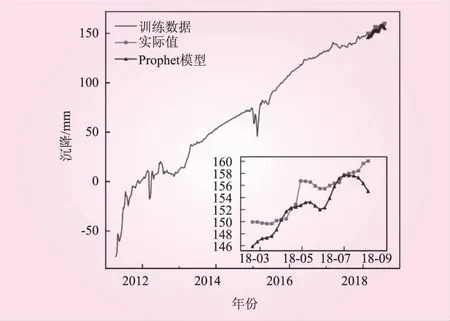
图6 测点SG1a-12预测结果

为展现Prophet预测精度，计算出多个测点的均方根误差RMSE均值为6.37 mm，平均绝对误差MAE均值为5.12 mm，平均绝对百分比误差MAPE均值为1.78%。计算出的各测点预测的残差均值见表1。从表1可知，误差都在毫米级，对于高堆石坝的影响几乎可以忽略不计，表明Prophet模型对于大坝变形具有较高的预测精度。

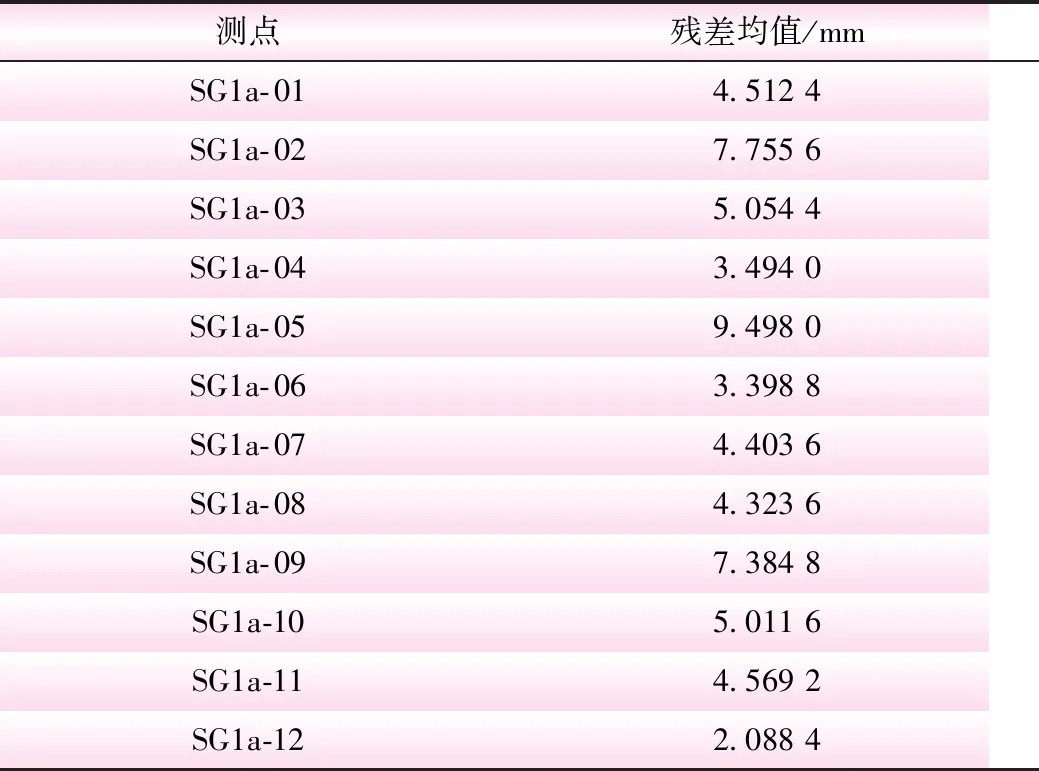
表1 预测残差均值

4 结 语

本文对江坪河水电站面板堆石坝的监测资料进行分析整理，利用Prophet模型和贝叶斯超参数优化对大坝变形进行预测分析。预测结果表明，利用机器学习模型预测堆石坝变形的误差范围在毫米级，对高堆石坝是可以接受的，且实施过程方便快捷，无需太多的人工干预。本文建立的面板堆石坝长期变形实时动态预测模型对高堆石坝全生命周期的性状评估与隐患及时预警具有一定的实用价值。