铝合金电缆与铜电缆不同排布方式下稳态载流量对比分析

梁经龙，刘 杰，黄位华

（中国能源建设集团山西省电力勘测设计院有限公司，山西 太原030073）

0 引言

电缆载流量是电缆最重要的电气参数，电缆载流量的分析计算关系到电缆容量的有效利用和安全可靠运行。在电缆稳态载流量的计算方法中，稳态热路模型计算方法的关键在于计算电缆各层和周围环境的热阻[1]，具有简单快速而直接等优点，但在边界、损耗等方面存在较大的简化处理，难以应用于复杂几何结构情况下的计算；数值计算法中有限差分法应用最早，但该方法不利于求解复杂边界问题和高梯度问题[2-3]；边界元法在复杂边界求解时，其边界太多会造成计算量较大[4-5]；有限元法适用于实际存在的各种复杂边界和耦合关系的计算，能应对各种复杂情况的建模，可在较低的计算成本下到达较高的计算精度[6-7]。文献[8-9]将稳态热路模型法和数值计算法相结合来确定电缆的载流量。

本文基于稳态热路模型法和有限元法，以单芯和三芯为例，分别计算水平、三角形排布的铜电缆和铝合金电缆在长期稳态载流量和短时过载载流量以及相同载流量时铝合金电缆的等效截面积，将铝合金电缆和铜电缆进行对比分析。

1 有限元法计算稳态载流量

采用有限元法计算直埋电缆的载流量。电缆直埋在土壤中，具有一定的埋深（以三芯电缆为例），几何模型如图1所示。

电缆本身与周围环境之间进行热传导形成的温度场由有热源区域和无热源区域组成，电缆线芯导体和金属护套层产生损耗并传热，为有热源区域，其温度场控制方程为

图1直埋三芯电缆几何模型

式中，T为温度，℃；qv为体积发热率，W/m3；k为导热系数，W/（m·℃）。

式中，P为电缆单位长度的损耗功率，分为导体线芯损耗和金属护套层损耗，W/m；S为导体线芯或者金属护套层的截面积，m2。

对于电缆其余层和土壤等无热源区域，使qv为0，得到其温度场控制方程为

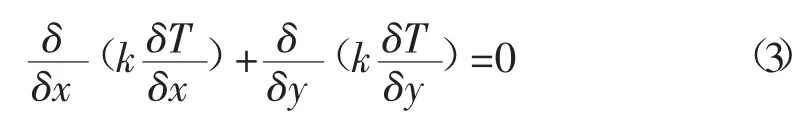
需要为方程给定边界条件使方程有唯一解。根据传热学原理，边界条件共分为3类，控制方程分别为[10]

式中，T0为恒温边界温度，℃；h为对流换热系数，W/（m2·℃）；Tf为流体温度，℃；qs为给定边界的热流密度值，J/（m2·s）；Γ∞为无穷远边界；ΓA为法向热流密度已知的边界；Γ12为流体温度和换热系数已知的边界。

如图1中，下边界与深层土壤温度相同，符合第一类边界条件；左右边界的法向热流密度为0，符合第二类边界条件；上边界为土壤与空气的分界面，符合第三类边界条件。

电缆线芯导体和金属护套层的电导率与温度相关，具体关系如下。

式中：σ为线芯导体或金属护套层Tc时的电导率，S/m；σ20为线芯导体或金属护套层20℃时的电导率，S/m；α为温度系数，1/K；Tc为电缆线芯导体或金属护套层的温度，℃。

线芯导体的温度特性是建立电磁场和温度场耦合的桥梁，温度上升导致线芯导体电导率改变，导体电导率会导致电缆体积发热率qv改变，从而影响温度场的变化，形成电磁场与温度场的耦合。

2 稳态热路模型法计算稳态载流量

目前IEC60287标准是国内外比较公认的电力电缆载流量计算标准，该标准给出了稳态热路模型用于分析和计算电缆载流量的方法。以直埋敷设单芯电力电缆为例，其模型见图2。

图2单芯电缆及其周围环境稳态热路图

对于单芯没有铠装层结构的电力电缆，铠装层损耗Wa和铠装层与金属套之间内衬层的热阻T2需要去掉，从高于环境温度的温升表达式中可以得到交流电缆安全运行的载流量，并且考虑电缆中载有负荷的导体数（等截面并载有相同的导体），从而得到电缆的计算公式为

于是得到

式中，Wc为电力电缆线芯导体单位长度的损耗，Wc=I2R，W/m；I为电缆载流量，A；R为导体在最高温度时单位长度的交流电阻，Ω/m；Wd为绝缘层单位长度的损耗，W/m；Ws为金属护套或屏蔽层单位长度的损耗，W/m；Wa为铠装层单位长度的损耗，W/m；T1为单位长度的绝缘层热阻，K·m/W；T2为金属护套与铠装层之间的热阻，K·m/W；T3为外护层的热阻，K·m/W；T4为周围介质与单位长度电力电缆表面之间的热阻，K·m/W；Δθ为导体与电缆外护套表面之间的温度差，℃；n为电缆芯数；λ1为金属套或屏蔽层中的损耗相对于线芯总损耗的比例系数；λ2为铠装层中的损耗相对于线芯总损耗的比例系数。

3 电缆稳态载流量对比计算

3.1 单芯电缆载流量对比计算

不同型号的单芯电缆的结构稍有不同，但大多包含有导体、绝缘层、半导体层、金属护套层、外护套层等结构。本计算采用的电缆为单芯电缆YJV-26/35kV-1×185，在仿真时应将电力电缆看作柱体，并要考虑径向温度变化。铜（铝合金）电缆的具体参数如表1所示，其中铜的温度系数为3.90×10-31/K，铝合金温度系数为4.29×10-31/K。基于表1建立模型并进行仿真计算。

表1单芯铜/铝合金电缆参数取值表

3.1.1 水平排布

当电缆水平排布时，电缆轴心距离土壤表面1 m，三相电缆轴线之间的距离是80 mm，对流换热系数取值为5 W/（m·K）；恒温边界为20℃；中间相温度最高为90℃时的电流即是稳态载流量，可以得到有限元计算单芯铜电缆水平排布的载流量为499.80 A，同样得到电缆线芯为铝合金时载流量为400.50 A。

采用IEC 60287标准在稳态热路模型计算出的单芯铜电缆水平排布的载流量为533 A，电缆线芯为铝合金时载流量为419.63 A，具体情况如表2所示。

以铜电缆的载流量为依据，计算导体为铝合金时达到同样的载流量所需要的截面积大小，即按照示例中使铝合金电缆载流量达到499.80 A时的截面积大小，稳态热路法计算时使铝合金电缆载流量为533 A时的截面积大小，有限元法计算结果为316.05 mm2，稳态热路法计算结果为317.94 mm2。

3.1.2 三角形排布

三相相互接触呈三角形排布是电缆另外一种常见的排布方式，取三角形的中心距离地面为1 m，除了排列方式改变外，其余参数与表1相同，可以得到有限元计算单芯铜电缆三角形排布的载流量为501.20 A，同样得到电缆线芯为铝合金时载流量为396.40 A。

采用IEC 60287标准在稳态热路模型计算出的单芯铜电缆三角形排布的载流量为512.80 A，电缆线芯为铝合金时载流量为405.80 A，具体情况如表3所示。

同样以铜芯电缆的载流量为依据计算等效截面积，有限元法计算的等效截面积为314.79 mm2，稳态热路法计算的等效截面积为316.05 m2。

表2单芯水平排布铜/铝合金电缆载流量计算参数表

表3单芯三角形排布铜/铝合金电缆载流量计算参数表

3.2 三芯电缆载流量对比计算

三芯电缆一般主要包含导体、绝缘层、金属屏蔽层、铠装层和外护层五大部分，以三芯电缆YJV43-3×120 mm2型XLPE电缆为例，电缆的具体参数如表4所示。

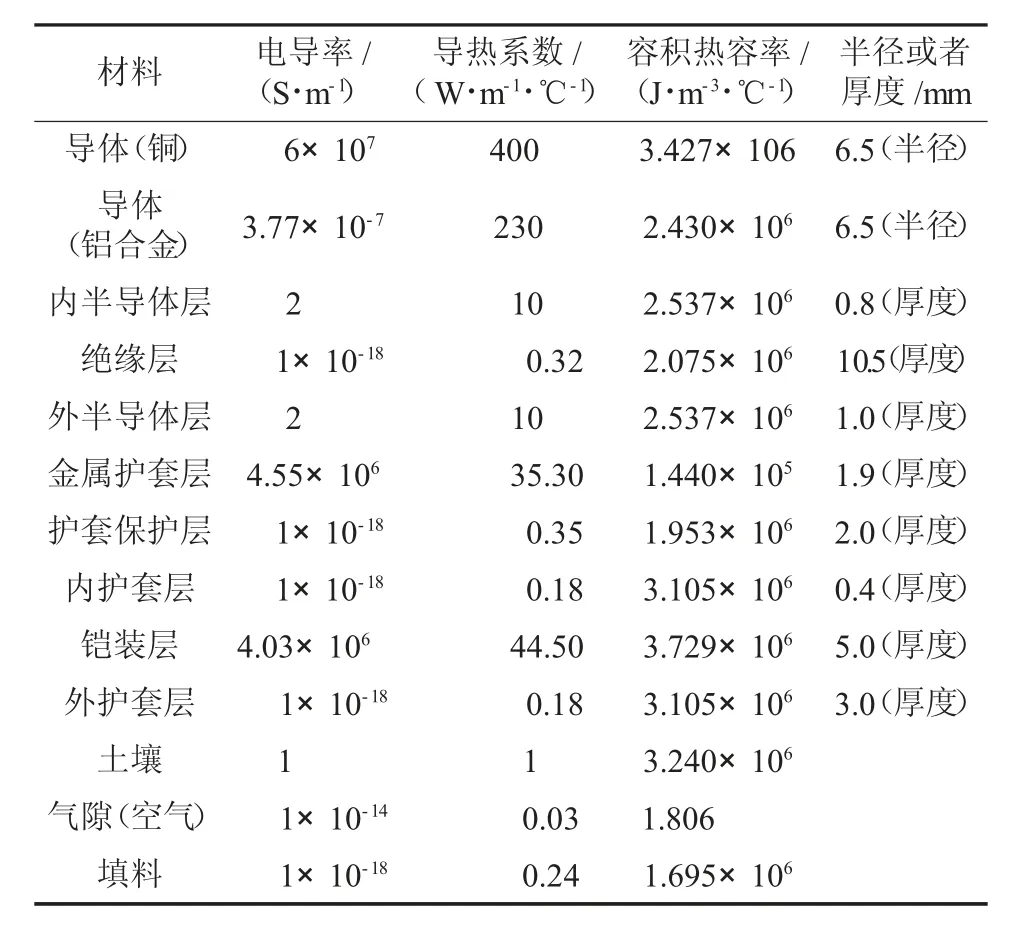
表4三芯铜/铝合金电缆参数取值表

电缆轴心距离土壤表面1 m，对流换热系数为5 W/（m·K），温度最高为90℃时的每相电流即是载流量。

由电阻温度系数来描述金属部分的电阻率随温度变化，铜的温度系数为3.90×10-31/K，铅护套的温度系数为3.86×10-31/K，高强度钢铠装温度系数为6.51×10-31/K，铝合金温度系数为4.29×10-31/K。可以得到有限元计算三芯铜电缆载流量为392.40 A，同样得到电缆线芯为铝合金时载流量为309.90 A。

采用IEC 60287标准在稳态热路模型计算三芯铜电缆载流量为403.30 A，电缆线芯为铝合金时载流量为321.30 A，具体情况如表5所示。

表5三芯铜/铝合金电缆载流量计算参数表

同样以铜电缆的载流量为依据仿真计算等效截面积，有限元法计算的等效截面积为206.63 mm2，稳态热路法计算的等效截面积为206.6 mm2。

电缆导体分别为铜和铝合金时，不同排布方式的单芯电缆和三芯电缆的稳态载流量的2种计算方法结果如图3a所示，以铜电缆计算结果为基准，铝合金电缆载流量和等效截面积与铜电缆的比值如图3b所示。

由图3可知，用2种方法计算3种情况的稳态载流量结果比较接近，最大误差不超过7%。由于铜的导电性能优于铝合金，所以相同截面积铜电缆载流量大于铝合金电缆，3种情况下相同截面积的铝合金电缆与铜电缆的稳态载流量比值均在0.8左右，达到相同的载流量时铝合金电缆的等效截面积与铜电缆的比值均在1.55左右，这是由导体的电气性能决定的，与排布方式和电缆芯数无关。

图3额定稳态载流量和等效截面积及其比值结果

4 短时过载载流量对比计算

电缆具有短时超出容许持续载流量的应急过载能力，在限定短时稳态过载情况下计算对应的载流量。限定铝合金电缆稳态短时过载温度为105℃和130℃时，计算相应的载流量。稳态短时过载温度为105℃时载流量、等效截面积及其各自比值结果如图4所示，稳态短时过载温度为130℃时载流量、等效截面积及其各自比值结果如图5所示。

通过研究铝合金电缆的过载特性，在限定短时稳态过载情况下计算对应的载流量，用2种方法计算3种情况的稳态载流量结果比较接近，最大误差不超过7%。在不同温度时，除线芯外其余的参数都相同的铝合金电缆的载流量与铜电缆的比值都在0.8左右，达到相同载流量时铝合金电缆的等效截面积与铜电缆的比值均在1.55左右，这是由导体的电气性能决定的，与限定的短时过载温度无关。相同载流量时铝合金电缆与铜电缆的导体质量比值为0.47左右。载流量变化的总体趋势是随着限定短时过载温度的增加而变大，但是这种增长是非线性的。电缆绝缘材料的使用寿命与工作温度是互相关联的，超过一定温度时绝缘材料的使用寿命会迅速下降，所以控制电缆工作温度以及短时过载的运行时间是很重要的。

图4短时过载105℃时稳态载流量和等效截面积及其比值结果

图5短时过载130℃时稳态载流量和等效截面积及其比值结果

5 结论

本文采用稳态热路模型和有限元法计算了2种电缆及3种排布情况下的载流量，结论如下。

a）用2种方法计算的稳态载流量结果比较接近，最大误差不超过7%。

b）相同截面积的铝合金电缆与铜电缆的稳态载流量比值在0.8左右，导体质量比值在0.30左右；相同载流量的铝合金电缆与铜电缆导体截面积比值在1.55左右，导体质量比值在0.47左右。这是由导体的电气性能决定的，与排布方式、电缆芯数和设定的电缆稳态运行温度无关。

c）铜的单位价格是铝合金的2～3倍，同等载流量下铝合金电缆仍然比铜电缆质量更轻、成本更低，铝合金电缆的主要优势是可以提高安装效率，降低制造和安装成本，具有良好的经济性能。