基于泰勒级数的系统电压稳定性分析
谢冬冬,宋 晓,荣家鹏
(国网焦作供电公司,河南 焦作 454000)
在进行电压稳定分析时,往往需要知道系统各负荷节点电压稳定强弱顺序,以便调度人员更合理采取控制措施。连续潮流法是求取系统电压稳定裕度的重要方法,此方法需要从系统运行基态点开始不断增加负荷,不断求解潮流方程,直致达到电压稳定临界点,具有计算量大且耗时的缺点[1]。文献[2]采用灵敏度法结合曲线拟合求取系统电压稳定强弱程度。以上方法不管是曲线拟合还是不断迭代,都要付出大量的计算代价。
本文用新的方法求出了系统电压失稳临界条件。首先求出节点电压与负荷电流关于负荷参变量的低阶导数,应用高等数学求导法则,得到系统动态等值阻抗;其次根据动态等值后的二节点系统图并结合基本电路原则,将戴维南等值电势展开为负荷参变量的泰勒级数;最后根据电压稳定的边界条件,解析出戴维南等值电势与负荷参变量的关系式,求出被观察节点最大负荷参变量,快速判断系统的电压稳定性及各节点电压稳定的强弱顺序。
1 动态等值参数的确定
1.1 系统动态等值模型
对于任意复杂系统网络都可以将其等值为由1个动态等值电压源经过1个动态等值阻抗向被研究节点提供电能的二节点等值系统,如图1所示。
根据数学理论,定义系统的动态等值阻抗为
(1)
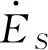
1.2 系统动态等值阻抗的求取
根据高等数学的求导法则,系统动态等值阻抗还可以表述为
(2)
式中:λ为负荷参变量,用式(2)重新定义动态等值阻抗的目的在于通过中间参变量转换克服电压与电流相量非解析的问题,这样便可通过式(2)顺利求出系统的动态等值阻抗。
电力系统在直角坐标下的潮流方程可以简单表示为
(3)
注入节点功率为
(4)

(5)
式中:J为常规潮流雅克比矩阵,由式(5)得:
(6)
在求解过程中,只是用到了潮流计算的雅克比矩阵因子表,故计算量将大大减少。
(7)
式中:Si为注入节点的复功率,符号^表示取共轭。则式(7)对λ求导,得:
(8)
将式(6)和式(8)代入式(2),求出系统的动态等值阻抗ZS。
1.3 动态等值电势对负荷参变量的泰勒展开式
当对系统进行动态等值时,相邻计算周期内动态等值阻抗变化很小,特别是在只有负荷端发生变化时,可以假定动态等值参数不变[1],得:
(9)
则式(9)对功率参变量λ求一阶二阶导数,得:
(10)
式(5)和式(8)对λ再次求导,得:
(11)
(12)
对式(11)变形得:
(13)
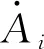
则动态等值电势关于负荷参变量的2阶泰勒级数展开式为
(14)
原则上泰勒级数展开式阶数越高,精度越高,但3阶及其以上导数计算将变得非常复杂而且对精度的影响也越来越小,兼顾计算速度与计算精度,故展开为2阶泰勒级数。
2 基于泰勒级数快速求取电压稳定裕度
2.1 最大负荷水平的解析求取
在图1中,将动态等值电势的相位作为参考相量,则由式(9)得:
(15)
式中:δi为所研究节点的电压相位角;Ris和Xis分别为动态等值阻抗的实部和虚部,将上式实部虚部分开,得:
Ui4+[2(PiRis+QiXis)-Eis2]Ui2+Zis2(Pi2+Qi2)
=0
(16)
电压有解的条件是方程判别式要大于等于0,即:
[2(PiRis+QiXis)-Eis2]2-4Zis2(Pi2+Qi2)≥0
(17)
假设节点功率保持同步增长,则有:
(18)
由式(17)得出临界条件,可迅速求出最大负荷水平与动态等值电势之间的关系:
(19)
式中:λi max为负荷节点i的最大负荷水平参变量;Eilj为对应于λi max状态下的动态等值电势,将式(14)代入式(19)即可求出最大负荷水平参变量λi max。需要说明的是初始功率越大,当前运行点离电压稳定临界点越近,求出的最大负荷水平参变量越准确。
2.2 节点电压稳定强弱顺序判别指标
对电力网络中每个待分析节点利用本文上述所提的方法,即可求出各负荷节点λmax,根据最大负荷参变量λmax的大小即可判断负荷节点电压稳定性强弱。最大负荷参变量越小,说明该节点距离电压稳定临界状态距离越近,电压稳定性越弱;最大负荷参变量越大,说明该节点与电压稳定失稳临界点距离越远,电压稳定性越强。通过比较各负荷节点所对应的最大负荷参变量即可判断出节点电压稳定的强弱顺序,重点监控那些薄弱节点将最有价值。
3 仿真算例分析
3.1 注入功率约束方程
为验证本文所提方法的可行性与有效性,将在系统同步功率扰动下进行仿真计算,并对其结果进行理论分析。
系统功率同步扰动:所有节点负荷功率恒比例增大,整个系统功率平衡由平衡节点完成。
对所有PQ节点i,有:
(20)
对所有PV节点j,有:
(21)
式中:λ为系统的功率控制变量参数,在基态时该值为1.0;Pi0和Qi0分别为初始情况下节点有功功率和无功功率;Pis和Qis分别为该时刻节点有功功率和无功功率;Qjcmin和Qjcmax分别为PV节点所约束的最小无功功率与最大无功功率,当PV节点无功越限时,PV节点转为PQ节点。
3.2 仿真分析
对IEEE14节点用本文算法进行分析,其中当λmax=1.783时,14节点系统的标准计算结果如表1所示。

表1 极限潮流标准计算结果
按照本文所提算法,系统潮流预测结果、负荷节点电压稳定强弱顺序分别如表2、表3所示。
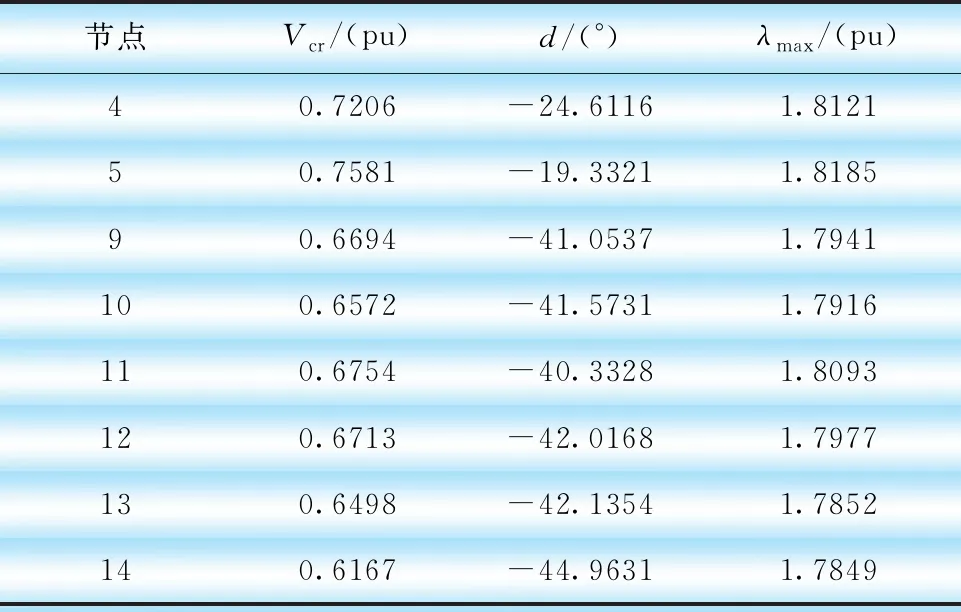
表2 极限潮流预测结果

表3 负荷节点电压稳定强弱顺序
根据仿真结果可知,节点14的最大负荷参变量最小、电压最低,实际距离电源节点最远,电压稳定性最差;节点5的最大负荷参变量最大、电压最高,实际与电源节点距离最近,电压稳定性最强。本文算法结果与真实结果具有一致性,说明所提理论的正确性。
4 结论
本文根据电压稳定的临界条件,解析出负荷参变量与动态等值参数之间的关系,从而求出被观察节点最大负荷,快速判断系统电压稳定性及各节点电压稳定的强弱顺序。此方法与其他分析电压稳定性方法相比,可以提前准确预知负荷水平,利于提前采取控制措施,具有计算速度快、时耗小、直观明了的特点。

