基于遗传算法的六自由度工业机器人轨迹优化研究

张景钰 马杰 桓茜

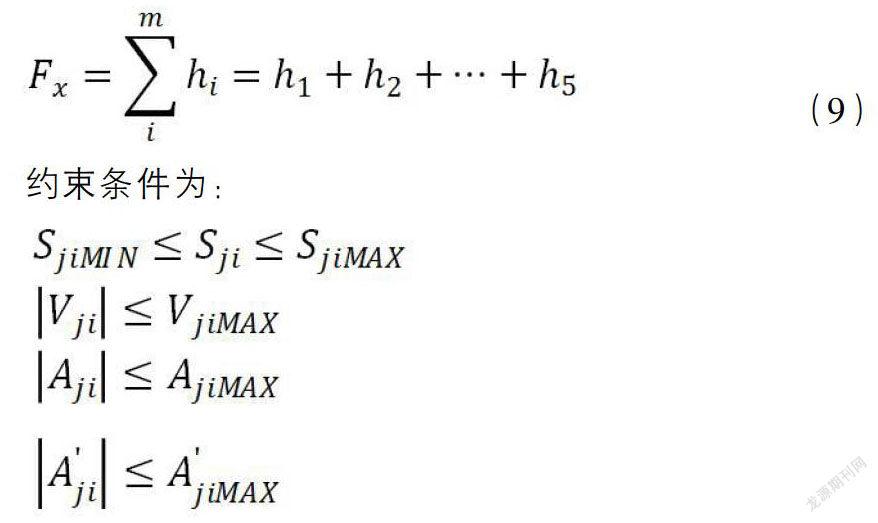
摘要：为了使雕刻工业机器人在轨迹运动中时间最短，我们推出工业机器人运动轨迹时间最优函数，求出约束条件，采用遗传算法对数学模型进行优化求解。最终得到一种工业机器人的轨迹规划方法，通过计算结果标明，相对于其他轨迹规划方法，工业机器人在进行雕刻作业时，时间缩短了21%，很好的满足了工程需要。

关键词：遗传算法;轨迹规划;工业机器人

0  引言

六自由度工业机器人在现今的工业生产中大量的得到应用，在汽车、3C等领域已基本实现了全机器人化。所以对六自由度工业机器人的轨迹规划有着重要的意义。

工业机器人的轨迹规划是指通过相关的算法，在空间坐标系中找到工业机器人最适合的运动路径，从而使工业机器人时间最短、路径最优、避免碰撞、不会有突变等情况发生。

本文我们给出了一种六自由度工业机器人的轨迹规划方法，首先运用五次多项式对轨迹进行拟合，再通过遗传算法求出时间最优情况下的雕刻工业机器人的轨迹路径，从而提高了雕刻效率。

1  五次多项式进行轨迹规划

我们将使用五次多项式插值对六自由度的工业机器人进行轨迹规划，在工业机器人的末端雕刻头上运动过程中，我们设置n个途径轨迹点，工业机器人经过每个轨迹点时，对应的时间为（t1，t2…tn）。然后每个点之间的间隔时间，我们记为h=ti-ti-1。六自由度工业机器人进行运动时，它会从起始点开始到终点结束，轨迹经过我们设置的轨迹点。工业机器人在某两个轨迹点之间的关节角度曲线函数我们记为Fi（t）。

在工业机器人的运动轨迹优化中，工业机器人在相应的位移、速度、加速度、加加速度等曲线中，不得出现突变、跳动的轨迹。相应的四条曲线应该保持连续性。这就给我们的路径轨迹规划提出相应的约束条件。

2  约束条件的设置

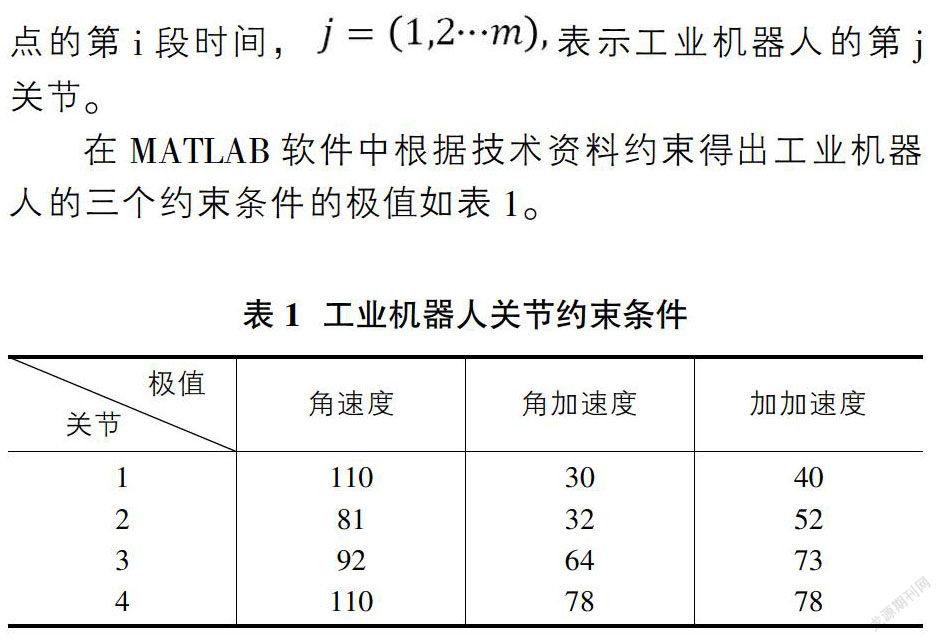
在工业机器人的实际工作过程中，它的每个关节角度、速度、加速度、加加速度有极限值。

在MATLAB软件中根据技术资料约束得出工业机器人的三个约束条件的极值如表1。

3  遗传算法的设置

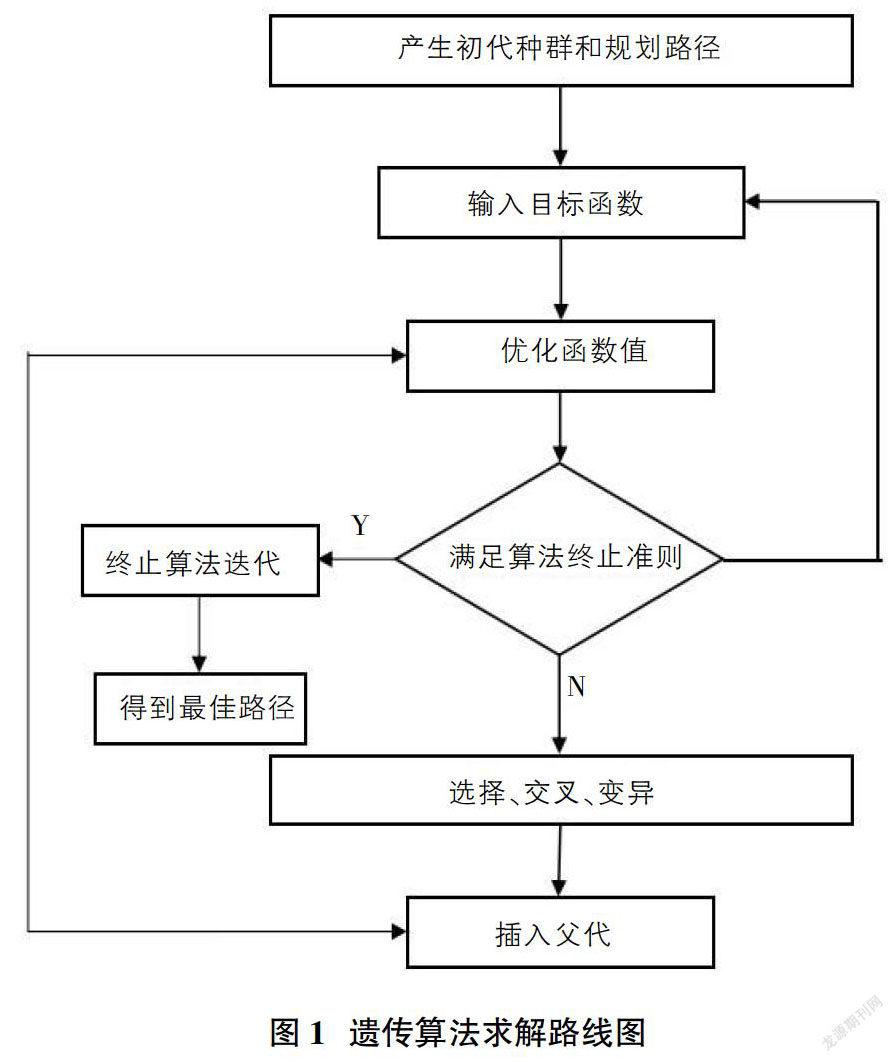
因为遗传算法的并行搜索，能在最优解的空间范围内的多个区域同时搜索信息，避免了常规算法陷入局部最优解的可能性。在本文中我们采用遗传算法对工业机器人的末端轨迹进行优化求解。

对工业机器人的末端轨迹时间间隔函数进行建模，确定优化目标时间最短。对其在满足约束条件的情况下使用遗传算法求解。具体的求解路线图1为产生初始的路径，然后在求解空间进行遗传算法求解。最终在位移、速度、加速度等的约束条件下得到最终优化解。

4  基于遗传算法的六自由度工业机器人轨迹规划分析

4.1 目标函数的建立

六自由度工业机器人末端依此通过设定路线的点，我们需要在时间最优的情况下，使工业机器人通过这些关键点完成我们既定的路径。所以我们可以得到该数学模型中的目标函数为

4.2 基于遗传算法的六自由度工业机器人轨迹规划仿真

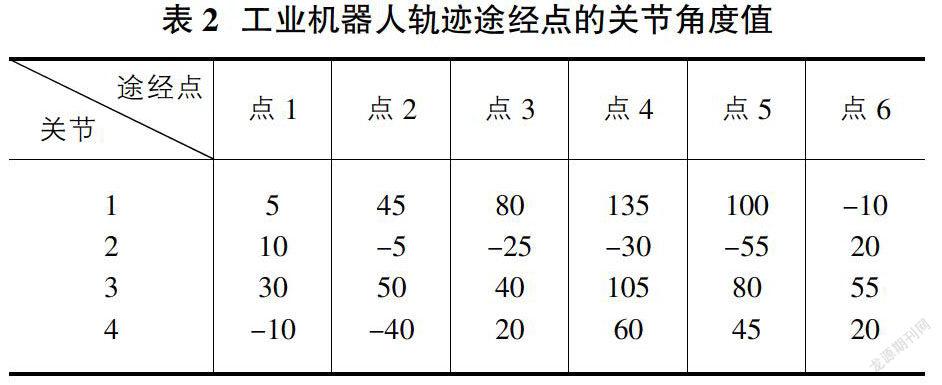
根据实际的加工情况，我们采用实验室一台ABB的六自由度雕刻机器人作为仿真对象。根据技术资料得到前四个关节在轨迹上必须经过点的参数如表2。

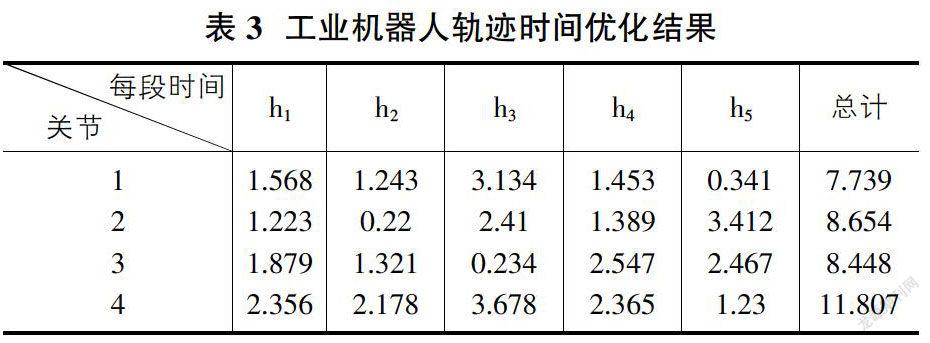
我们编写遗传算法适应度函数代码，在MATLAB算法工具箱中使用遗传算法在满足约束条件的前提下，对时间最优这一目标函数进行轨迹优化求解，最终得到的优化结果如表3。

根據研究中得到的工业机器人的运行时间对比发现。我们采用遗传算法求得的结果比原来运动时间减少了21%，同时满足约束条件。

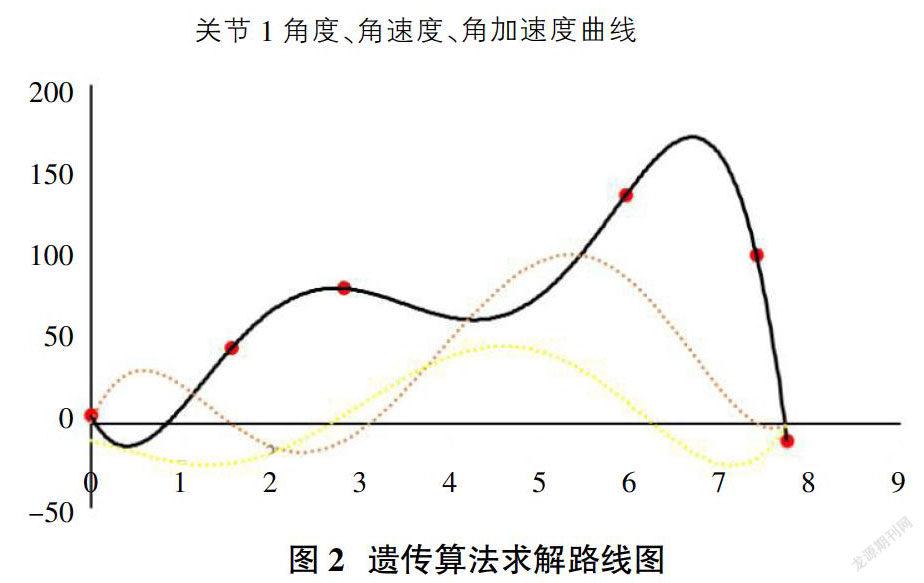
我们将时间和每个途经点的角度值代入五次多项式中，可以得到每个五次多项式的系数。所以最终我们得到前四个关节的函数曲线图2，为关节一的曲线图。单位角度（°）、角速度（°/s）、角加速度（°/s2）。

从优化后的曲线可以看到，关节角度、角速度、角加速度曲线平滑过渡，而且在起始和终止都是基本从0开始到0结束满足了工业机器人的平滑运动的要求。

5  结论

①推导出五次多项式插值的工业机器人的轨迹规划公式，继而求出角速度、角加速度、加加速等函数。建立对此类工业机器人轨迹规划时的数学建模问题。

②利用遗传算法对六自由度雕刻机器人的轨迹进行了优化求解，得到前四个关节运动时间变化情况，得到了相应的角度、角速度、角加速度等曲线。给此类问题提出了解决方案，为了工程上的应用提供了一种新的思路。

参考文献：

[1]刘贝贝，袁亮，孔庆博，吴金强.6自由度工业机器人运动轨迹优化方法研究[J].组合机床与自动化加工技术，2020（02）：11-15.

[2]郭勇，赖广.工业机器人关节空间轨迹规划及优化研究综述[J].机械传动，2020，44（02）：154-165.

[3]党宏社，张梦腾，候金良，白文静.工业装配机器人轨迹规划算法研究[J].现代电子技术，2019，42（08）：63-67.

[4]于海璁，陆锋.一种基于遗传算法的多模式多标准路径规划方法[J].测绘学报，2014，43（01）：89-96.

[5]陈丹.基于遗传算法B样条曲线优化在机器人轨迹规划中应用[D].武汉科技大学，2007.