智慧交通短时流量预测研究
孟祥玉 杨婷婷 刘学朗 曹露



摘 要:随着我国经济的快速发展,城市化进程的不断加深,城市交通的负担也越来越大,科学的进行交通规划和诱导已经成为目前各城市交通管理部门研究的重要内容。合理规划诱导的前天便是对交通流量进行科学有效的预测,本章主要针对小波神经网络展开研究分析,对交通流量预测在智慧交通中的作用进行的阐述,将小波神经网络的具体模型分析展开了详细的研究,经过研究目前小波神经网络可以准确科学的对城市交通流量进行预测。希望笔者的研究能给短时交通流量预测的研究人员以参考。
关键词:智慧交通;神经网络;小波函数;短时流量预测
一、引言
随着经济的不凡增长,家庭可用于支配的收入也越来越多,随之私人车辆的数量也是逐年攀升,再加之外出频率和出行距离的不断增加,引起了现代交通的严重拥堵问题,交通拥堵已经成为各大城市迫切解决的主要问题之一,通过对交通流量的准确分析研究,对建立高效的道路设施解决拥堵,有效缩短人们出行的交通时间成本有着至关重要的意义[1]。伴随着我国城市化进程的不断深入,城市以及郊区机动车的数量均逐年增长,佳通堵塞的范圍越来越大,拥堵问题是愈演愈烈。中大城市在机动车种类众多,公共汽车服务质量恶化的背景下,这给公路交通也带来了极大的危机,很多城市都出现了混用道路的不良现象,非机动车、机动车混用道路情况日益严重。交通规划和土地利用明显的不协调[2]。
因为交通流量存在这偶然性,短期性、上下班集中性等特征,所以在交通流量的观测工作中,AI智能技术被越来越广泛地应用到各个领域中,也被更多的人所了解和认识。也被认为是未来可以替代交通预测模型的更好方式,然而,在诸多的研究方法当中,目前应用最为普遍的便是神经网路技术,为了有效解决混合流量下的交通问题,开发一个能适应目前交通现状的短时交通流量预测模型迫在眉睫,新的预测模型不仅可以帮助制定高速公路的交通规则,还可以很好的对交通设施的服务质量给予评估,而且,还可以给交工工程师在交通规划工作中参考。表征非稳态交通的特征的基本要素是:交通量、速度以及交通密度。这些数据的预测可以帮助了解交通网络中可能发生变化的性质,由此来有效的对交通的堵塞和交通事故进行缓解。而目前,多数的交通预测模型都是基于均匀交通流所进行的,而这并不适用非均匀交通的情况[3]。
二、交通拥堵的原因
导致城市交通拥堵的原因主要有:汽车使用率增加、道路容量不足或设计不妥、道路交会处过多。其中随着私家车的增多车辆的使用率不断增加是导致现代城市交通拥堵的主要因素,由于汽车方便出行,大家的日常出行像旅游、上班、去超市购物等等大都是开车,虽然方便了自己,却导致城市日常车流升高,加之城市道路的容量设计不足或是设计不妥,结果就是城市道路无法负荷这么大流量的车流量,从而也就成就了现在的城市交通拥堵现象。再加上城市道路的设计大都是辐射状,这样的设计虽然方便了市郊的车辆往来,但是,一旦是车辆往来高峰,就会导致郊区的车辆不断地涌往城市主干道路,结果道路上就堵满了来自郊区的通勤车辆,车流拍成长线就显而易见了。同时城市内道路的交叉口过多,红绿灯也就相应的多,再加上路口间红绿灯的设置不合理就是增加道路拥堵的状况[4]。
三、交通流量预测在智慧交通中的作用
伴随着城市经济的快速发展和私家车的逐步增多,城市交通的供需不平衡日益严重,城市交通带给人们的体验越来越差,交通拥塞、交通事故、交通污染、出行停车难等等的诸多问题成为了各大城市当下最迫切解决的问题,也成了各城市交通管理部门的重要关注点。比如,在交通较为集中的十字路口,怎样才能更好或是更为灵活应用当下的检测设备,监测相关车流情况获取有效的通行车辆数据,进而通过对这些数据的交通态势和交通流量的分析,对城市道路实现实时的分析,成为当下的主要研究课题[5]。
四、预测模型分析
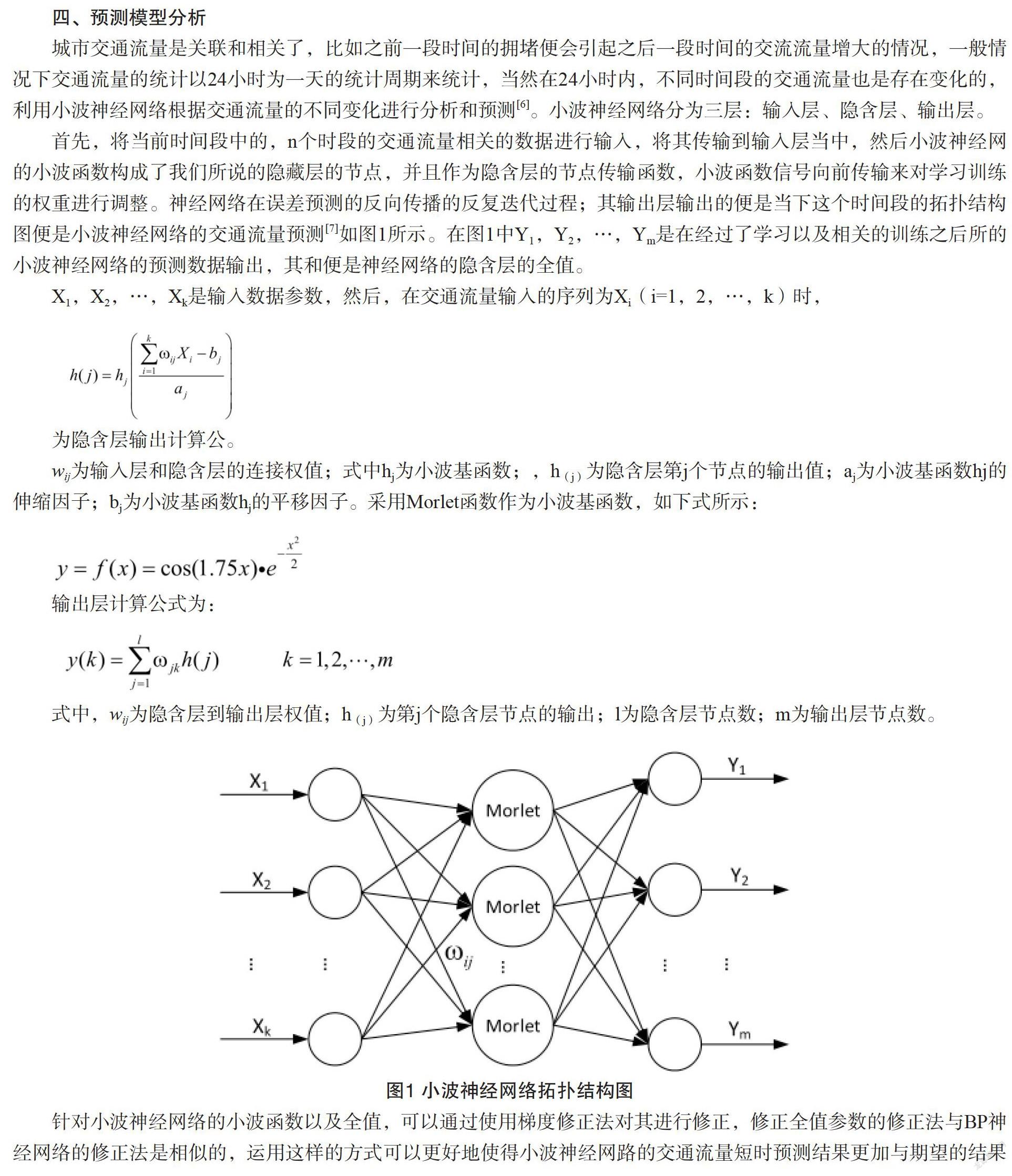
城市交通流量是关联和相关了,比如之前一段时间的拥堵便会引起之后一段时间的交流流量增大的情况,一般情况下交通流量的统计以24小时为一天的统计周期来统计,当然在24小时内,不同时间段的交通流量也是存在变化的,利用小波神经网络根据交通流量的不同变化进行分析和预测[6]。小波神经网络分为三层:输入层、隐含层、输出层。
首先,将当前时间段中的,n个时段的交通流量相关的数据进行输入,将其传输到输入层当中,然后小波神经网的小波函数构成了我们所说的隐藏层的节点,并且作为隐含层的节点传输函数,小波函数信号向前传输来对学习训练的权重进行调整。神经网络在误差预测的反向传播的反复迭代过程;其输出层输出的便是当下这个时间段的拓扑结构图便是小波神经网络的交通流量预测[7]如图1所示。在图1中Y1,Y2,…,Ym是在经过了学习以及相关的训练之后所的小波神经网络的预测数据输出,其和便是神经网络的隐含层的全值。
五、小波神经网络的灵敏度分析
针对小波神经网络的输出以及输入,包括其相关权重的相关程度评价便是小波神经网络的灵敏度,他是对输入参数发生变化时确定模型输出的响应。为了把不相关的输入及时的消除掉可以通过训练后的网络进行敏感度分析来解决这一问题。如此一来消除掉了不相关的输入不仅使网络的运行效率和性能得以提高还可以降低成本。除此之外,该项分析还可以及时的了解到输入变量与输出之间的基础关系[8-9]。本次研究采用的是小波神经网络模型对敏感性进行的分析。对预先训练的MLP网络的均值进行了敏感性分析。此批处理其他输入都固定在各自的平均值上。改变其平均值±1的第1个输入,所有计算出平均值上下各50步的网络输出[10-11]。然后再根据每个输入对此过程进行反复重复。对各个输入变量的变换进行总结,并且根据其灵敏度进行分析,其中9个最重要的输入参数分别是数字商用(SLCV)、日(DY)摩托车速度(SSM)公共汽车速度(SB)、时间(TM)、轿车/吉普/货车体积(C/J/V)、两轮车速度(STW)等(图2)。在进行下一步时,小波神经网络的测试和训练应该采用与神经网络模型中最佳选择的模型相同的神经网络配置,仅仅只对其灵敏度进行考虑的分析中发现了9个最为重要的相关输入,新模型的具体训练以及测试的结果如图3所示。试验结果显示,即使输入的数量不断减少从19一直减少到9以后,这种模型的表现相对于旧模型来说也是非常棒[12].
六、仿真及结果
本次研究通过预测模型的分析搭建,通过取每15分钟没的一次短时间的交通流量,然后,再在一天之内对同一个交通流量采样点取样的数据为96个,然后再利用这些所采样的短时交通流量数据对我们的小波神经网络给予训练,之后,将我们已经完成训练的小波神经网络在之后的一天进行运用,将其运用到当天的交通流量预测工作当中去[13]。
通过5000次的训练,得到训练有效权重对流量数据的学习训练验证,然后将达到的各个权重值运用到后续的交通流量预测工作当中,发现运用其所得到的陈流量相关的数据与实际的交通流量数据值差值(如图4所示)也比较小,明显可以看出在交通流量较小的时段占比偏差略有升高,但是總体结果还是非常理性的[14-15]。
七、结束语
综上所述,在交通问题日益成为城市的焦点问题的背景下,搭建小波神经网络预测模型,科学的对交通流量预测及指导,运用目前的短时交通流量数据训练验证,来指导相应的交通流量预测工作,进而对交通诱导进行精准的指导。本文进过对小波神经网络的研究发现,采用小波神经网络进行预测的结果与实际值极其接近,运用小波神经网络可以准确科学的对短时交通流量进行预测。
参考文献:
[1]马建,孙守增,芮海田.中国交通工程学术研究综述.2016[J].中国公路学报, 2016,29(6):1.
[2]ZHANGJ,WANGFY,WANGK.Data-DrivenIntelligentTransportationSystems:ASurvey[J].IEEETransactionsonIn-telligentTransportationSystems, 2011,12(4):1624.
[3]谢印庆,姜莉,王鲁云.一种快速车流量检测算法[J].哈尔滨理工大学学报, 2016,21(4):19.
[4]康维新,杨文彬,李鹏.交通流量远程发布系统设计[J].哈尔滨理工大学学报, 2012,17(5):39.
[5]柳长源,孔凡宁,冯晋文.基于GPS和SD卡存储的交通信号采集系统[J].哈尔滨理工大学学报, 2017(3):25.
[6]唐毅,刘卫宁,孙棣华.改进时间序列模型在高速公路短时交通流量预测中的应用[J].计算机应用研究, 2015,32(1):146.
[7]郭海锋,方良君,俞立.基于模糊卡尔曼滤波的短时交通流量预测方法[J].浙江工业大学学报, 2013,41(2):218.
[8]GHOSHB,BASUB,O’MAHONYM.MultivariateShort-TermTrafficFlowForecastingUsingTime-SeriesAnalysis[J].IEEETransactionsonIntelligentTransportationSystems, 2009,10(2):246.
[9]姚卫红,方仁孝,张旭东.基于混合人工鱼群优化SVR的交通流量预测[J].大连理工大学学报,2015(6):632.
[10]殷礼胜,何怡刚,董学平.交通流量VNNTF神经网络模型多步预测研究[J].自动化学报, 2014,40(9):2066.
[11]谢印庆,姜莉,王鲁云.一种快速车流量检测算法[J].哈尔滨理工大学学报, 2016,21(4):19.
[12]康维新,杨文彬,李鹏.交通流量远程发布系统设计[J].哈尔滨理工大学学报, 2012,17(5):39.
[13]段艳杰,吕宜生,张杰.深度学习在控制领域的研究现状与展望[J].自动化学报, 2016,42(5):643.
[14]唐少虎,刘小明,陈兆盟.基于计算实验的城市道路行程时间预测与建模[J].自动化学报, 2015,41(8):1516.
[15]刘霞.复杂非线性系统的小波神经网络建模及应用[D].大庆:大庆石油学院,2005

