地铁站台地震响应动力模拟分析
陈俊


摘 要:对于地下结构空间的开发和利用在城市地铁建设中越来越普遍,其地下结构的安全问题尤为突出,特别应重视地震作用下结构的安全性。本文主要利用有限元软件ADINA对地铁站台进行地震动力响应数值模拟,为地下结构设计与施工提供参考价值,并为地铁站台运行安全性评定提供依据。文中主要对地震作用下站台竖向位移、结构顶板变形以及结构顶板的动力分析来进行模拟分析。
关键词:地铁站台;地震响应;有限元模拟
中图分类号:TU311.3 文献标识码:A
0 引言
随着我国经济建设的迅猛发展,城市规模和人口的高速增长,给城市交通带来了越来越重的压力,为了缓解这种压力,地铁这种快捷、便利的交通方式成为首要选择,在其广泛应用的同时使得其安全性显得尤为重要,近年来地震灾害现象表明,地下结构在强地震作用下可能会出现严重的震害及次生灾害,城市大型地下工程的抗震安全性已成为备受关注的社会问题之一。
本文以某地铁站台为工程背景,运用ADINA有限元软件,模拟其在EI-Centro波形地震荷载作用下的动力响应,分别对站台中心X方向和Y方向上的位移、速度和加速度时程曲线进行分析,为地铁站台抗震工作提供参考价值。
1 计算方法和原理
用于地下结构开挖、支护过程的数值分析方法有有限元法、边界元法、有限元—边界元耦合法。本文选取的ADINA主要采用有限元法,它除了求解线性问题外,以分析非线性和多场耦合问题著名。其主要原理是将结构都划分为若干个单元,然后根据能量原理建立单元刚度矩阵,并形成整个系统的总体刚度矩阵,从而求出系统上各个节点的位移和单元的应力,其可以模拟各种施工过程和各种支护效果,同时可以分析复杂的地层情况和材料的非线性等[6]。
目前按照对于荷载处理方法的不同,荷載和结构模型大致有两种:第一种是主动荷载模型,即不考虑围岩和支护结构的相互作用,因此,支护结构与主动荷载作用下可以自由变形,和地面结构的作用没有什么不同。这种模型主要适应于围岩与支护结构的“刚度比”较小的情况,或是软弱底层对结构变形的约束能力较差时;另一种是主动荷载加围岩弹性约束的模型,认为围岩不仅对支护结构施加主动荷载,而且由于围岩和支护结构的相互作用,还对支护结构施加被动的弹性反力。
目前地震反应分析方法主要分为静力法、反应谱法和时程分析法[7]。时程分析法动态模拟较为准确,但其计算量大,通常应用于特别重要结构或不规则结构或其他特殊情况。反应谱法理论上只适用于弹性结构的抗震分析,用于非弹性情况必须进行修正,而时程分析法可直接应用于弹塑性结构的抗震分析计算。我国抗震规范推荐采用反应谱法和时程分析法[8-9]。本文采用的时程分析法,也称直接动力法,它是根据动力学运动方程,将地震波时程记录作为激励,直接积分求解结构在各个时刻的动态响应。
2 工程概况
本文以某一地铁站台1:10模型为例,建立有限元模型,对其进行地震响应分析。地铁站台模型尺寸为2.2 m×0.6 m
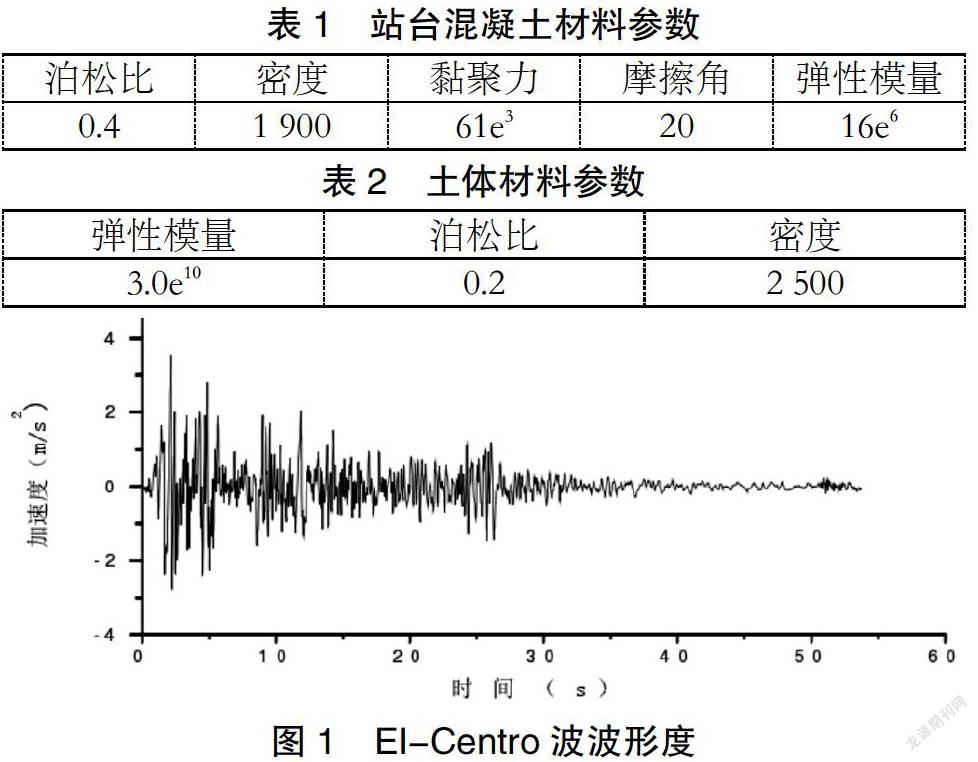
×0.4 m,中柱为边长0.026 m的正方向断面,柱间距为0.25 m,柱有7根,最外中柱距车站断面的距离为0.35 m,站台顶板厚0.03 m、中楼板厚0.015 m、底板厚0.03 m、侧壁厚0.02 m。土体宽度为2.4 m,高度为1.2 m;模型相应的材料属性见表1、2所示,荷载为有重力荷载和地震荷载两部分组成,其中重力荷载即对整个模型施加9.8 m/s2的重力加速度,地震荷载即对模型施加EI-Centro水平加速度波(见图1所示)。
本文中模型建立主要包含自由度定义、几何模型的建立、约束与荷载定义、材料属性和划分单元部分。单元库中有多种单元类型,常用单元类型有线单元,包括梁、杆等壳单元平面单元,包括平面应力单元、平面应变单元等三维实体单元等。需要根据不同的问题选取合适的单元类型,本文的计算对象为平面应变,因此将土体离散成若干四边形单元,用的三维实体单元来离散地下结构。
3.1 定义自由度
在本文三维实体单元中,勾取X/Y/Z方向的平动,忽略其在不同方向上的转动,如图2所示。
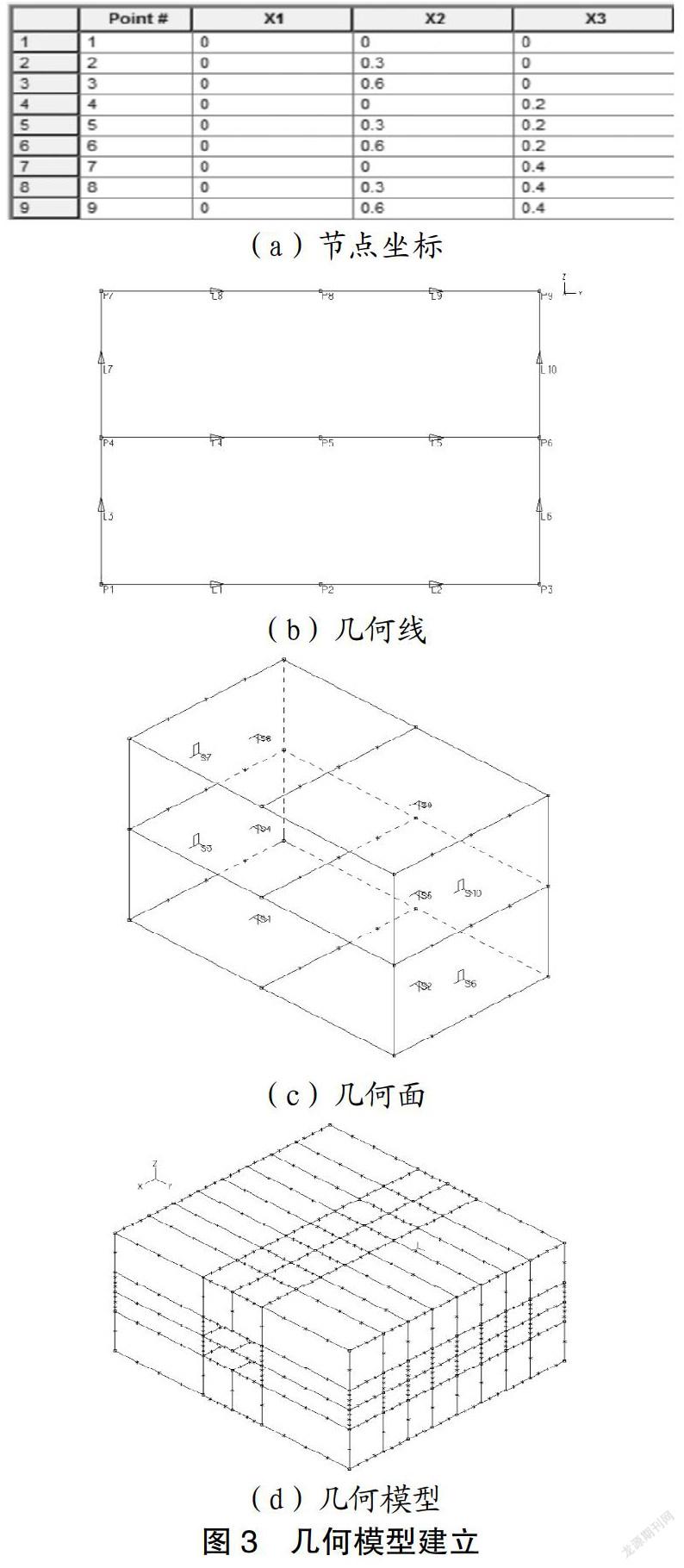
3.2 创建几何模型
本文中几何模型的具体建立,即依次定义几何点、几何线、几何面、几何体和立柱,节点输入坐标值如图3(a)所示,采用选点法建立相应的几何线如图3(b)所示,在其基础上采用延伸类型扩展为几何面,如图3(c)所示,采用同样方法将几何面延伸扩展为几何体,最后定义地铁站台空间立柱,得到最终的几何模型如图3(d)所示。
3.3 定义约束与荷载
在几何模型建立完善后,要对边界条件施加相应的约束条件,忽略转动影响因素,本文中主要有三种类型约束,分别为X方向、Y方向和Z方向上平动约束,对其相应的边界面施加边界约束。定义荷载部分主要包含两部分,即结构本身的自重荷载和地震荷载;自重荷载定义为9.8,方向为Z轴负方向,保证自重荷载永久性存在,定义其时间函数为1。
在定义地震荷载之前,要先定义时间函数,将EI-Centro波形地震荷载文件导入,随后定义时间步,如图4所示。其中,图中第一行数值为1的时间步是计算重力作用下结构的反应,将地震荷载按照50个步数,步长为0.02进行施加,时间步总数为2。特别需要注意的是地震荷载要将施加方式设置为Ground Acceleration(如图5所示)。
3.4 定义材料
本模型中涉及到混凝土和土体两种材料,具体按照表1和表2给出的参数进行输入。
3.5 划分单元
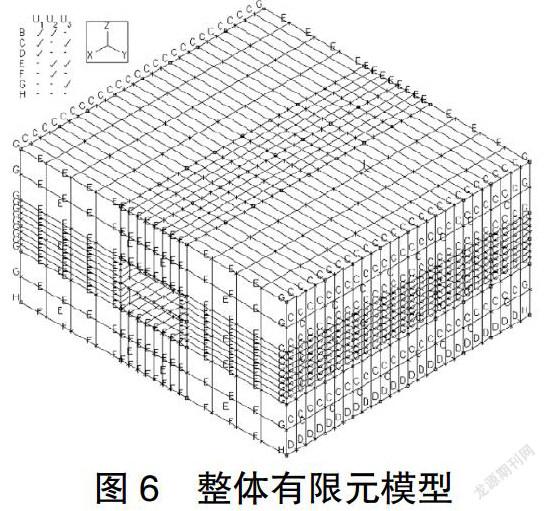
本文划分单元先对顶板、底板、中板、侧壁、立柱和土体分别进行定义单元组,再依次进行划分单元。对立柱采用进行线划分,对顶板、底板、中板和侧壁采用4节点单元进行面划分,对土体采用3-D Solid类型,进行8节点体单元划分。生成的整体有限元模型如图6所示。
4 求解结果与分析
4.1 站台位移云图
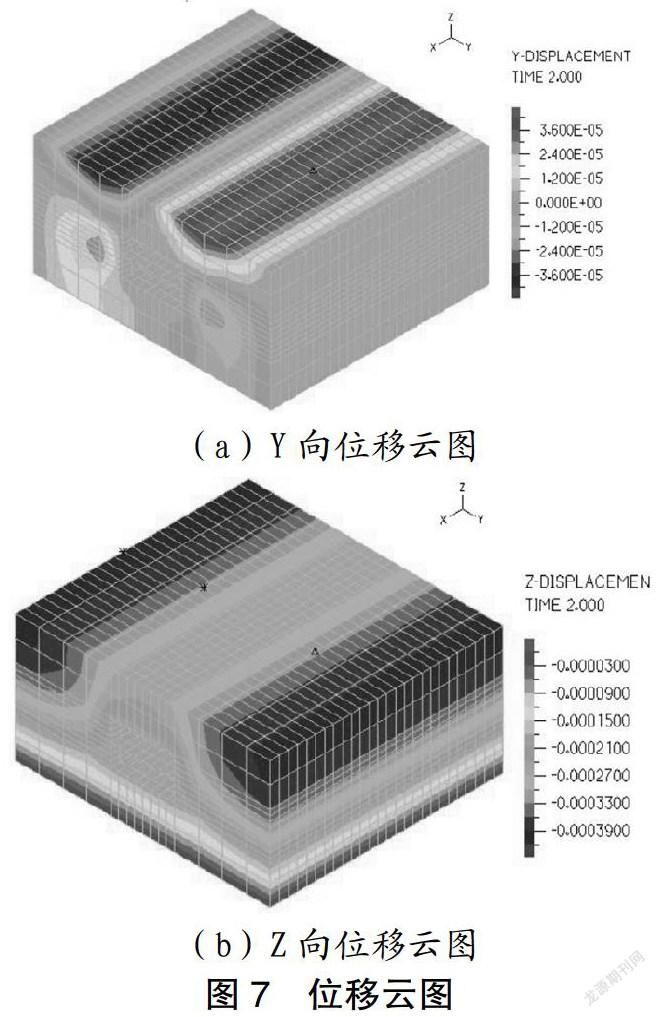
从图7可知,Y方向最大位移主要出现在顶板立柱左右侧中心位置,其次位移较大处为中板两侧中心位置;Z方向最大位移主要出现在顶板边缘位置,且其底板位移变化较为均匀。比较两个方向上的位移可知Z方向位移比Y方向位移大得多。
4.2 车站应力分布
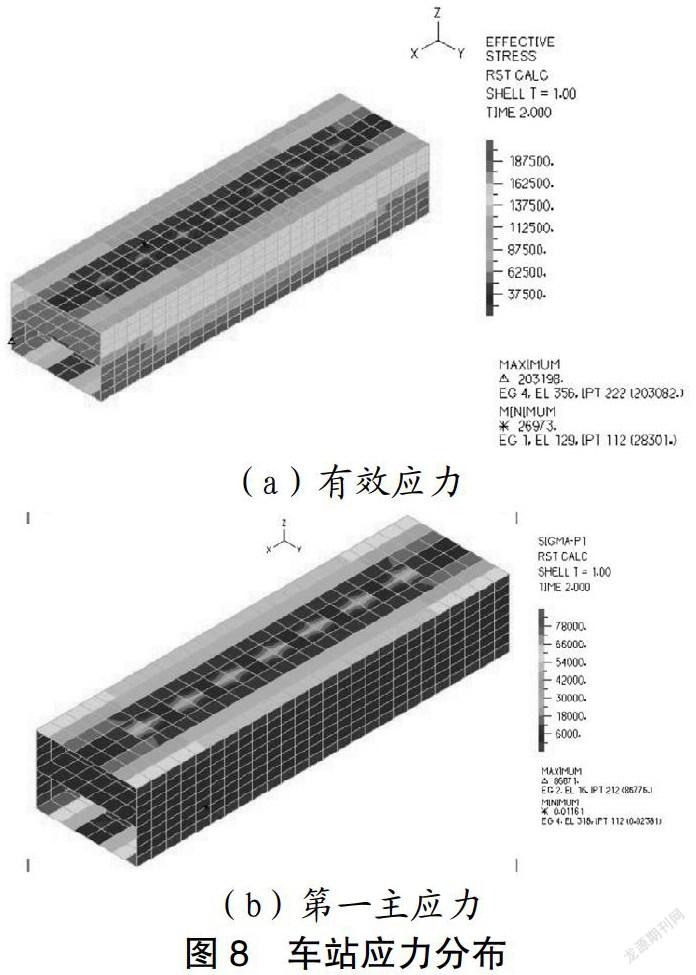
从图8可见,车站侧板有效应力较大,且其随Z向深度的增大而逐增,中板有效应力相对较均匀,车站顶板和底板有效应力向中心位置逐减。顶、底板第一主应力相对其他部位较大,且与侧板耦合处应力达到最大值。
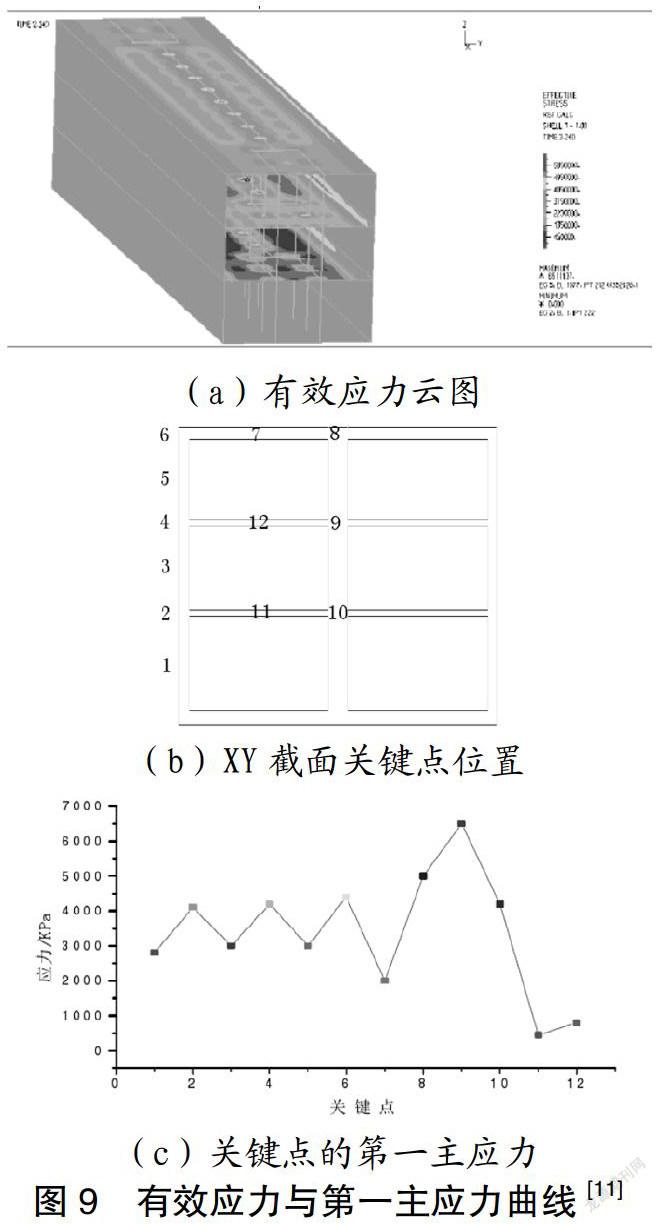
图9为文献11中的有效应力云图与关键点上的第一主应力曲线,文献11中的地震波主要为修正后的EI-Centro波形,且地下结构为三层,对比图9发现,有效应力大小受地震波和层数的综合影响很大,图9中的有效应力最大区域主要发生在中、上层板,侧板均匀且较小;比较第一主应力大小,可知最大第一主应力为9点(即上层中立柱底板),其次为8点(即顶板中部)与本文结论较为一致。
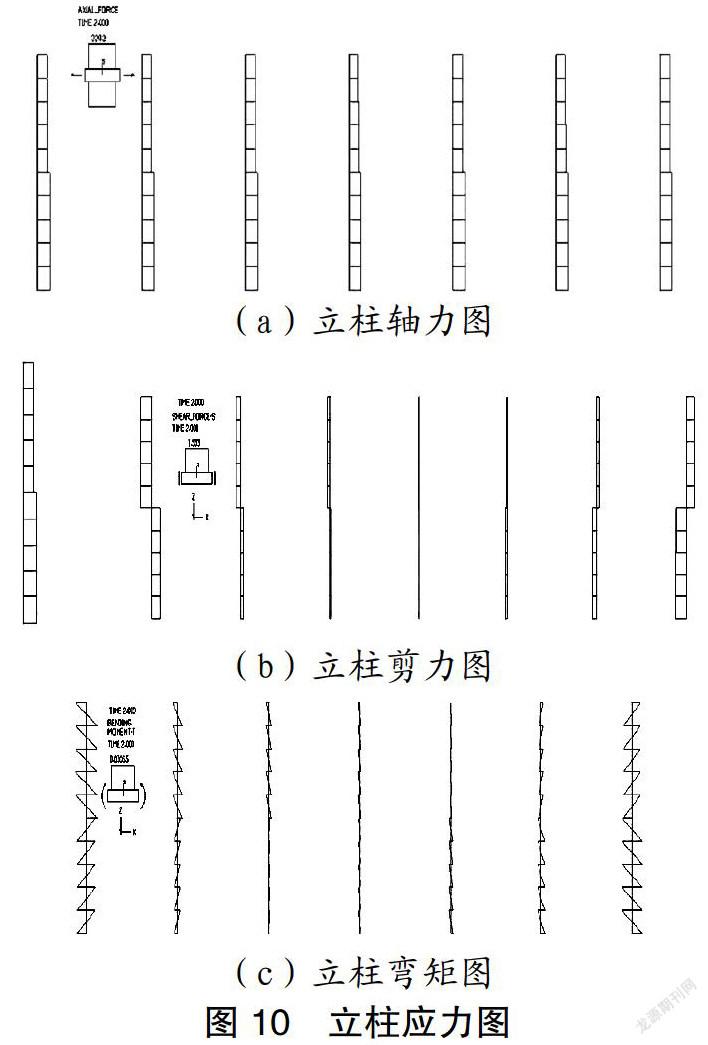
4.3 立柱内力图
图10为立柱内力图。从图可见,两侧立柱轴力大于中间立柱,且上层轴力小于下层;剪力和弯矩在两侧分别达到最大值,且向中心处逐渐减小。
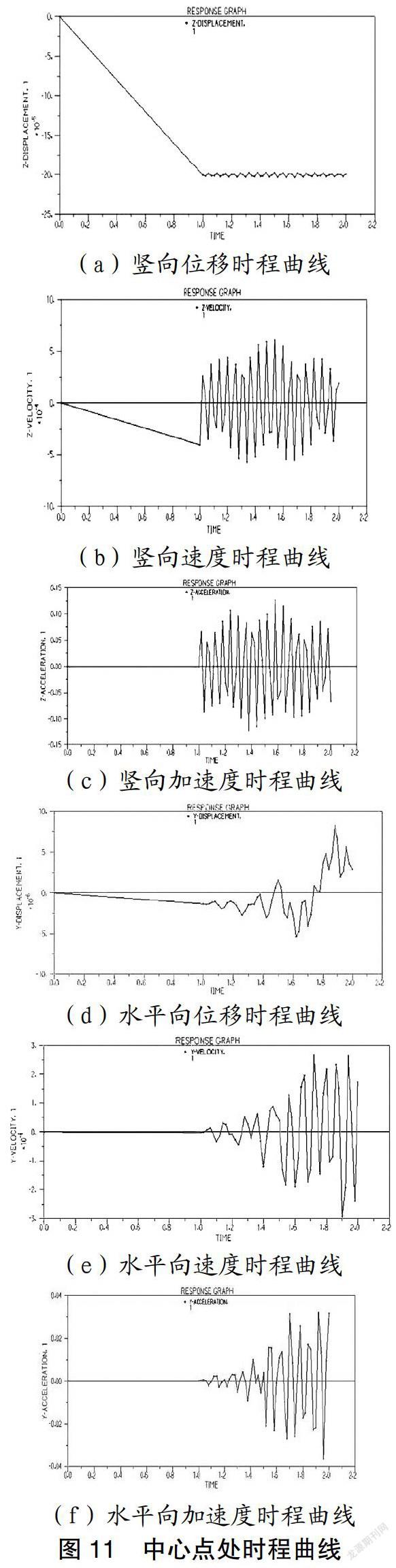
4.4 时程曲线
图11为竖直和水平向时程曲线。从图可知,站台中心竖向位移呈现先线性先增加后趋于稳定,即竖向位移受地震动力影响不大;站台水平位移也呈现先线性增加,但其较竖直方向增加速率较小,随后受地震动力影响较大,呈现出上下波动的现象,竖向和水平向速度与加速度在地震波施加后上下波动都比较明显。
5 结论
本文通过ADINA进行地铁站台地震动力响应数值模拟,以动力有限元方法为基准,比较了不同地震波形响应的影响,得到以下结论:
(1)在站台位移云图中可知,Y方向最大位移主要出现在顶板立柱左右侧中心位置;Z方向最大位移主要出现在顶板边缘位置,底板位移变化均匀。Z向位移整体都较Y向位移大得多。
(2)在车站应力分布图中,得出地下结构顶板中部的变形和应力较大,且与侧板耦合处应力达到最大,加速度响应也最大。站台侧板有效应力较大,且随Z向深度的增大而逐增,中板有效应力相对较均匀,站台顶板和底板有效应力向中心位置逐减。
(3)两侧立柱轴力大于中间立柱,且上层轴力小于下层;立柱的剪力和弯矩在两侧分别达到最大值,且向中心处逐渐减小。
(4)站台中心竖向位移呈现先线性增加后趋于稳定,即受地震动力影响不大;站台水平位移也呈现先线性增加,但其较竖直方向增加速率较小,随后受地震动力影响较大,呈现出上下波动的现象。
(5)从整个结构来看,车站顶板、各角隅处最容易发生破坏。因而在设计和施工过程中应对上述部位予以重视。
参考文献:
[1]栾茂田,李湛,范庆来.土石坝拟静力抗震稳定性分析与坝坡地震滑移量估算[J].岩土力学,2007,29(02):224-230+236.
[2]閆转平.土石坝地震动力响应及稳定性分析研究[J].陕西水利,2013,82(05):107-108.
[3]刘小生,赵剑明,杨玉生,等.基于汶川地震震害经验的土石坝抗震设计规范修编[J].岩土工程学报,2015,37(11):2111-2118.
[4]李万红,汪闻韶.土石坝非线性动力反应分析[J].水利学报,1994,39(02):24-30.
[5]李湛,栾茂田.土石坝地震永久变形计算方法[J].水力发电学报,2009,28(04):63-70.
[6]孙均,吴逸群.岩土介质中应力波传播问题的有限元法分析[J].岩土工程学报,1983,5(04):28-42.
[7]张春霞,李昌铸,卢铁瑞,等.现行桥梁抗震设计的反应谱分析方法[J].公路交通科技(应用技术版),2008,25(09):8-10+23.
[8]中国建筑科学研究院.建筑抗震设计规范(GB/50011-2001)[S].中国建筑工业出版社,2008.
[9]王松涛,曹资.现代抗震设计方法[M].中国建筑工业出版社,1997.
[10]胡文源,邹晋华.时程分析法中有关地震波选取的几个注意问题[J].南方冶金学院学报,2003,24(04):25-28.
[11]林宇晗.城市地铁车站地下结构地震反应分析[D].辽宁工程技术大学,2013.

