焊接式闭式叶轮应力优化分析

徐涛 陈世凡

摘要：压气叶轮作为压缩机的主要部件，主要受离心力影响。通过仿真计算在不改变气动参数的前提下，带有8个叶片的闭式离心叶轮，在离心荷载作用下，分析了叶顶倒角、轮盖厚度、轮盖倒角对叶轮的强度影响。经过分析，发现在叶片进口叶顶位置应力最大。为了减小叶轮局部位置上最大应力，对叶片与轮盖的连接处倒圆进行了分析。进一步对轮盖的几何结构重新优化设计，分析结果证明盘侧厚度增加有利于提高叶轮强度;通过改进整体叶轮外形，叶片进口处的应力集中现象得到大幅度的改善。

Abstract： Impeller is one of the most important parts of compressor which mainly affected by centrifugal force. The influence of tip chamfer， cap thickness and cap chamfer on the strength of a closed centrifugal impeller with 8 blades was analyzed under centrifugal load without changing aerodynamic parameters. It is found that the maximum stress is at the tip of the inlet blade. In order to reduce the maximum stress on the part of the impeller， the inverted circle between the blade and the wheel cover was analyzed. The geometric structure of the wheel cover is optimized and the results show that the increase of the thickness of the side of the wheel is beneficial to the improvement of the impeller strength. The stress concentration at the inlet of the blade can be greatly improved by improving the shape of the impeller.

关键词：闭式叶轮;离心力;强度分析;优化

Key words： closed impeller;centrifugal force;strength analysis;optimization

0  引言

压缩叶轮又称工作轮，是离心式压缩机中唯一对气流做功的元件是转子上的主要部件[1～3]。一般由轮盘、轮盖和叶片等零件组成。气体在叶轮叶片的作用下，随叶轮做高速旋转，气体受旋转离心力的作用，以及在叶轮里的扩压流动，使它通过叶轮后的压力得到提高[4]。

国内外已经进行了关于压气叶轮的叶片的形线设计、CFD流场分析、叶片的强度分析等，但是关于叶轮在离心荷载作用下，自身尺寸，比如叶顶（根）倒角、轮盖厚度、轮盖倒角，对叶轮的应力影响程度研究较少[5～7]。

基于此，本文借助ANSYS有限元软件，对压气叶轮在离心荷载作用下，叶顶（根）倒角、轮盖厚度、轮盖倒角对叶轮应力的影响程度，找到较为合适的叶轮尺寸。对今后的叶轮设计具有较大的工程应用价值。

ANSYS功能强大，操作简单方便，现在已成为国际最流行的有限元分析软件，在历年的FEA评比中都名列第一。目前，中国100多所理工院校采用ANSYS软件进行有限元分析或者作为标准教学软件。

1  离心力

离心力（Centrifugal Force）是一种“虚拟力”或称惯性力，它使旋转的物体远离它的旋转中心。在牛顿力学里，离心力曾被用于表述两个不同的概念：在一个非惯性参考系下观测到的一个惯性力，和向心力的反作用力。在拉格朗日力學下，离心力有时被用来描述在某个广义坐标下的广义力。在通常语境下，离心力并不是真实存在的力。但是根据广义相对论原理，惯性力作为与引力的等效力，是真实存在的。

相对转动的非惯性系中的物体，所受离心力为F=m？棕2r，其中？棕表示非惯性系自身转动的角速度，m为物体质量，r为圆周运动的半径。需要注意的是，该离心力方向为沿半径背离圆心。

2  模型简介

本文中所提的叶轮为离心式压气叶轮，属于焊接闭式叶轮。叶轮由轮盖、轮盘和叶片组成。

2.1 叶轮模型

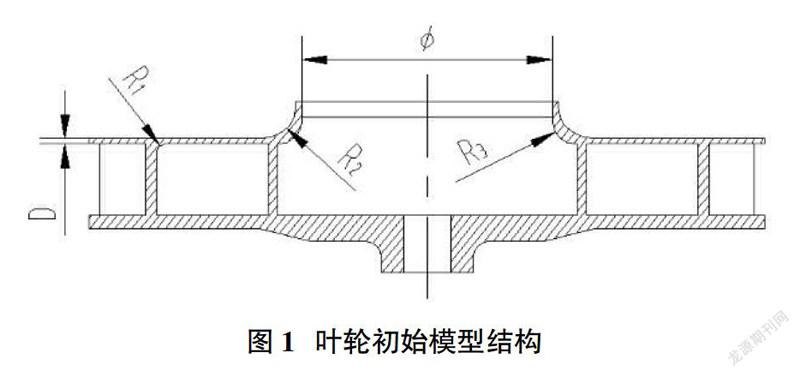
本文中所需优化的闭式离心压气叶轮（见图2）由轮盖、轮盘和叶片三部分组成。轮盘中心与轴连接的那一部分称为轮毂。闭式叶轮的原始模型中，轮盖、轮盘与叶片的交接处无倒角，即图2中的R1不存在。但为方便理解后续叶轮尺寸优化过程，在图2中加上倒角R1。由于叶轮流道内部参数决定气动性能，为了改善叶轮的应力分布，只能对其外形进行修改，即叶轮叶片的厚度，型线以及图2所示的进口直径φ等参数都不允许更改。因此，本文重点分析了叶顶倒圆、轮盖的型线及其厚度等参数（即R1、R2、R3和D）对最大应力的影响，尽量使其满足强度设计要求。

2.2 几何边界条件

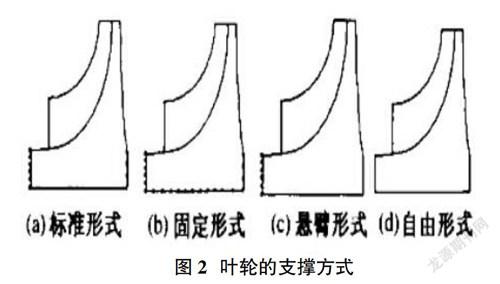
对于一个有轴孔的压气叶轮而言，在应力的分析中，转动轴的支撑方式，也就是轴孔的约束形式必须和实际叶轮的支撑形式相吻合。目前，压气叶轮支撑方式有4种，如图2所示。

（a）标准形式：压气叶轮两轴向端面固定（即两端面的沿X、Y、Z轴平移为0，绕X、Y轴转动为0），叶轮整体能绕轴线（Z轴）转动，取轴线方向为Z轴。

（b）固定形式：压气叶轮两轴向端面与轴孔固定（即两端面与轴孔的沿X、Y、Z轴平移为0，绕X、Y轴转动为0），叶轮整体能绕轴线（Z轴）转动，取轴线方向为Z轴。

（c）悬臂形式：压气叶轮进口轴向端面固定（即两端面的沿X、Y、Z轴平移为0，绕X、Y轴转动为0），叶轮整体能绕轴线（Z轴）转动，取轴线方向为Z轴。

（d）自由形式：压气叶轮两轴向端面及轴孔不受约束，叶轮转动时处于自由状态。

3  叶轮应力优化分析

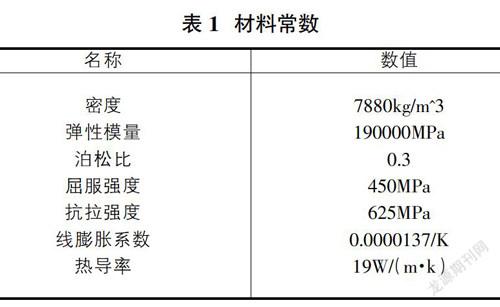
压气叶轮材料采用双相不锈钢2205（00Cr22Ni5Mo3N），

其相关材料如表1所示。

3.1 初始叶轮应力分析

离心压气叶轮几何形状非常复杂，相应的受力情况也很复杂，其中主要有高速旋转产生的离心载荷，而由其动力产生的压力载荷和温度效应产生的热应力都非常小[8]。文献[9]指出由气动力产生的压力载荷和热应力不应该忽略，但其计算同时也表明，压力载荷和热应力非常小，在其计算结果中由压力载荷和热应力产生的应力强度只占叶轮总应力的2%。因此本文进行的强度研究，在计算中只考虑由高速旋转产生的离心载荷。

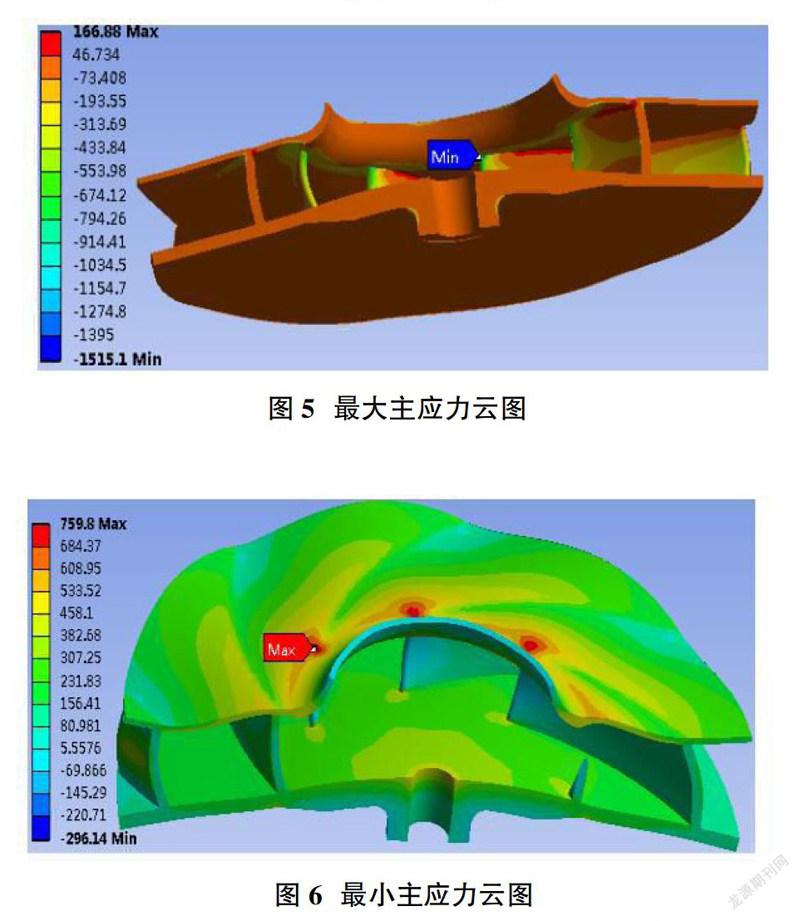
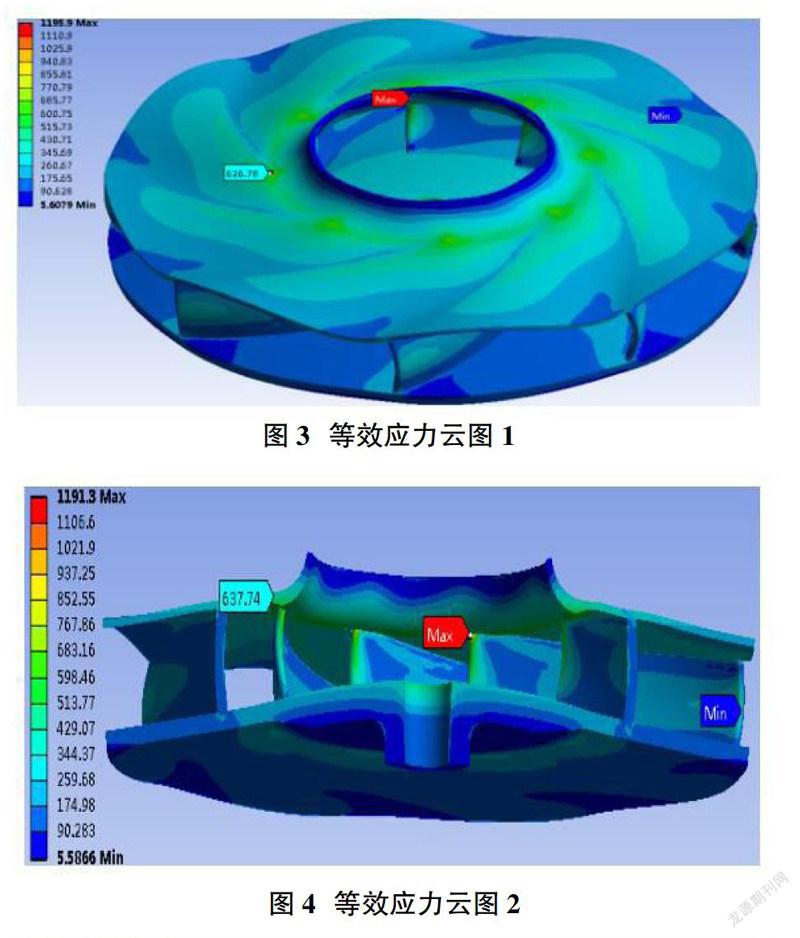
图3～图6给出了本文所需优化的闭式叶轮初始模型的应力分布。

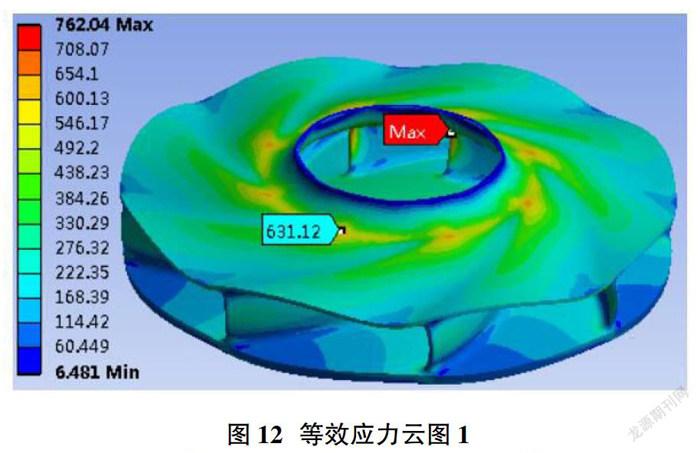
由图3～图4得到，初始叶轮的等效应力最大为1191MPa，出现在进口叶片与轮盖连接处，此区域较小，每个连接处仅小范围存在。高应力区域为叶片与轮盖连接处，以及进口倒角（R3）处，该应力区域范围较大，应力范围为429～630MPa。

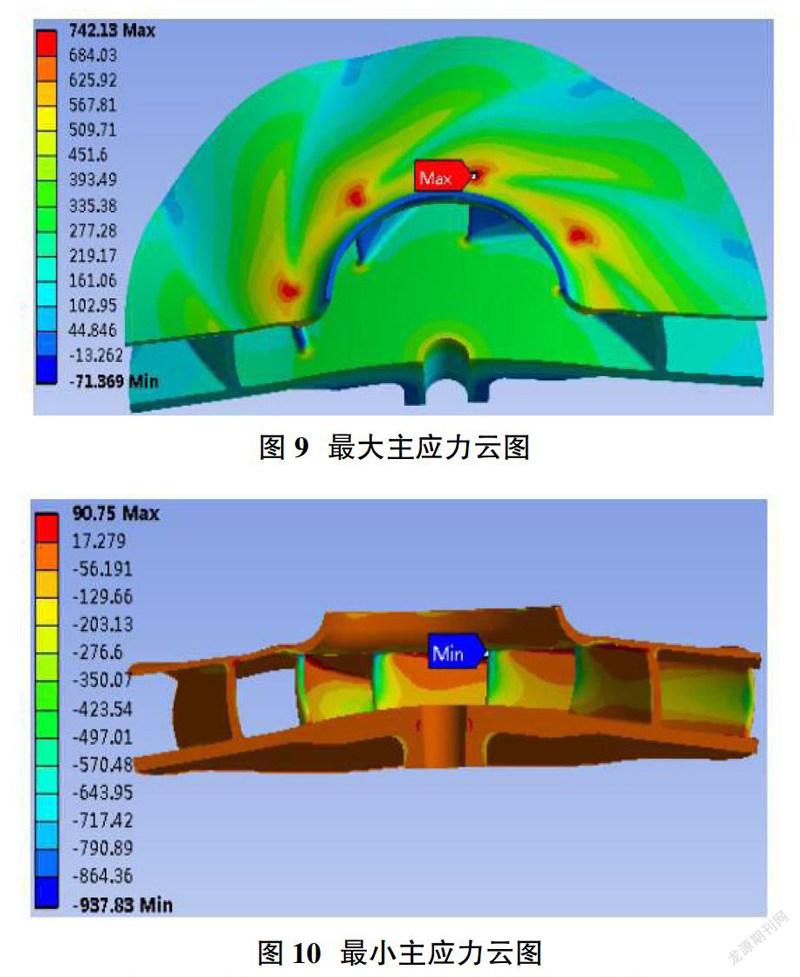
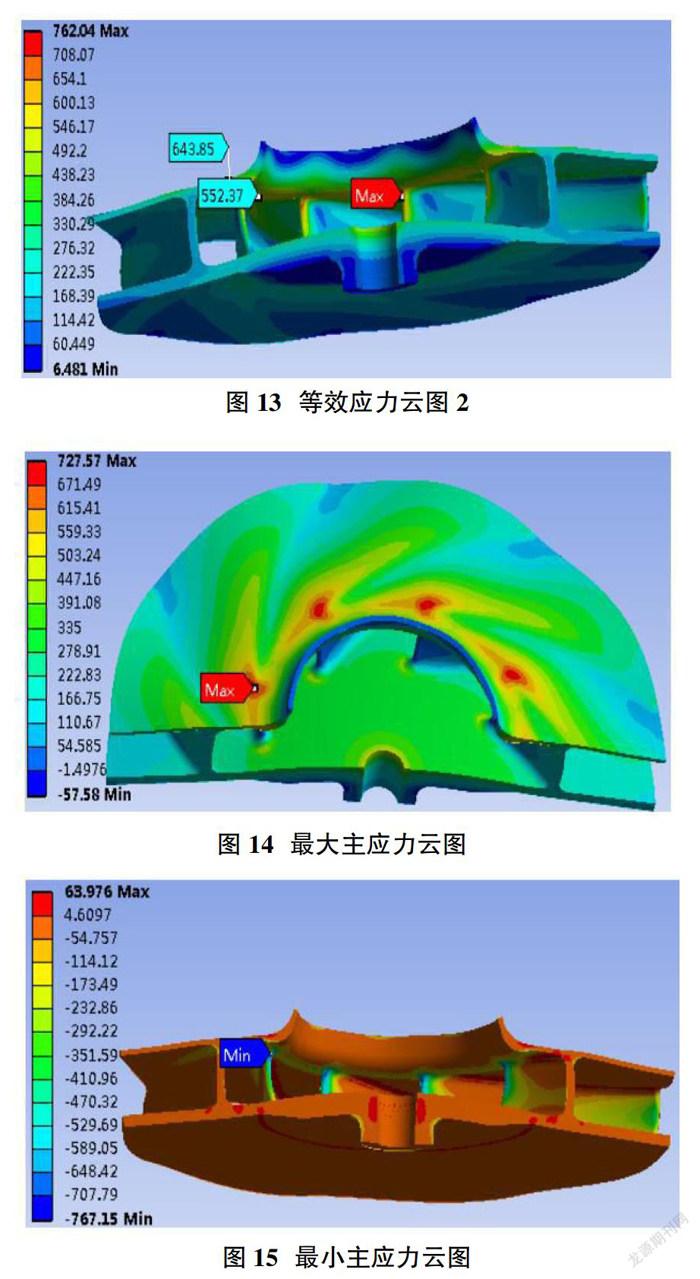
图5显示叶轮最大主应力分布情况，可知最大拉应力位于进口叶片所对应的轮盖表面，数值达760MPa。

图6显示叶轮最大压应力分布情况，可知最大压应力（1515MPa）位于进口叶片与轮盖连接处，该应力位置等同于等效应力云图中的最大等效应力位置。

轮盘与叶片的连接处并未出现较大应力区域，猜测这是由于轮盘表面造型不同于轮盖且厚于轮盖而造成。

初步推测：①初始叶轮的最大等效应力主要由压应力贡献;②进口叶片与轮盖连接的高应力可能是由于叶顶处未倒角和轮盖较薄造成的;③进口倒角（R3）处的高应力可能是由于轮盘质心位于进口倒角（R3）处，且此处壁厚较薄导致的。

根据上述推测，现改变R1、R2、R3与轮盖厚度D这四个参数，对叶轮进行优化分析。

3.2 叶顶（根）倒角R1对应力影响的分析

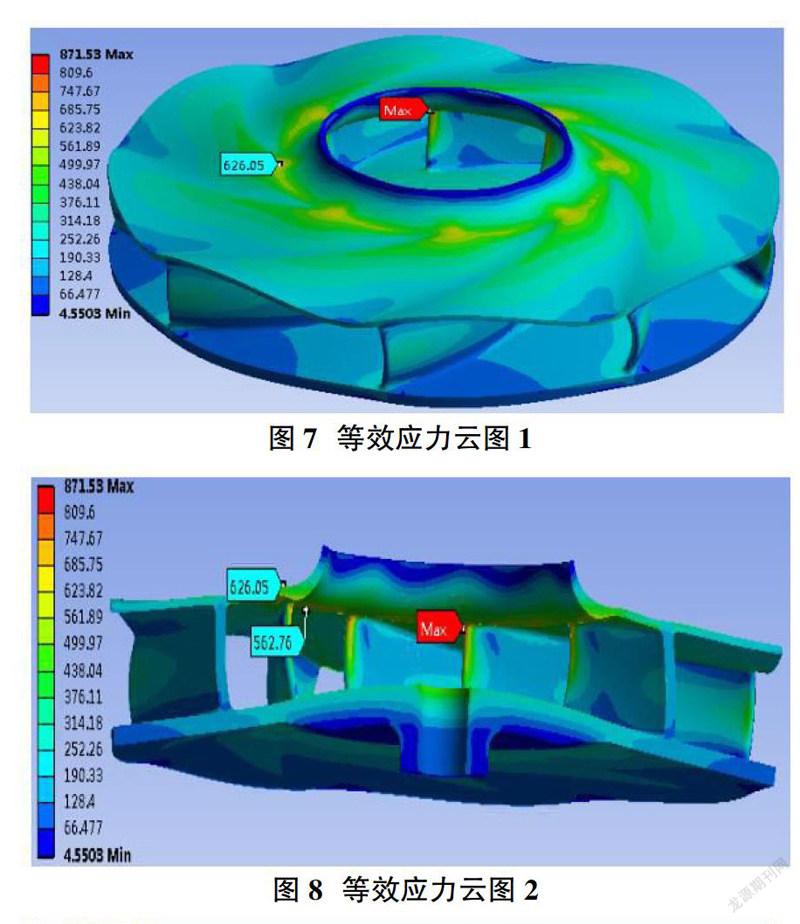
针对叶顶（叶根）倒角R1计算了R1=3mm，R1=4mm，R1=5mm，R1=6mm，R1=7mm这5种结构的叶轮应力情况，叶轮其余参数不变，保持一致。图7～图10为R1=3mm时，叶轮的应力分布云图。

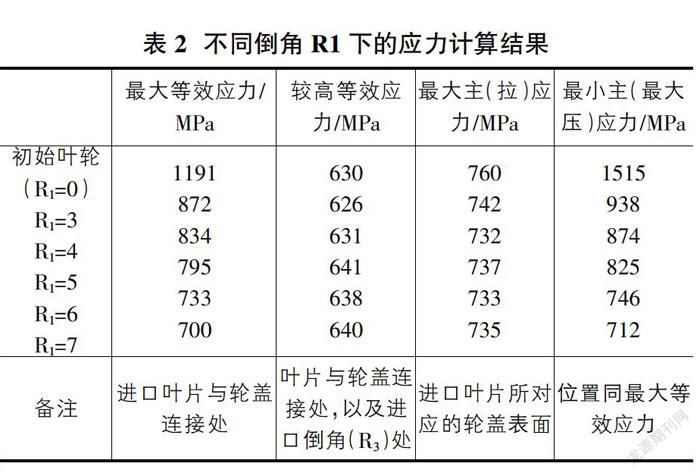
以上不同倒角R1下的应力计算结果见表2。

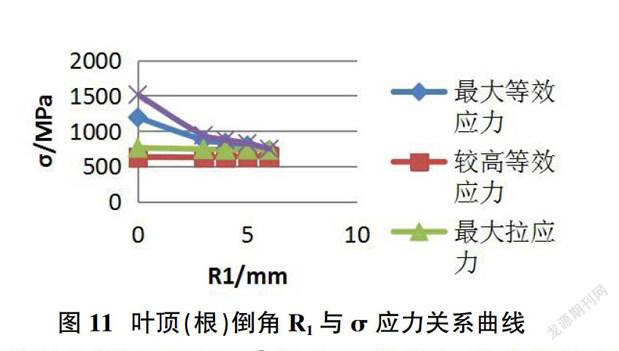
根据表2，整理数据得到以下关于设计参数R1与应力？滓的关系图。

从以上数据可看出：①随着R1的增大，最大等效应力与最小主应力（最大压应力）数值明显减小。如果增大倒角R1的尺寸，可以降低压应力50%;②随着R1的增大，最大拉应力与较高等效应力无明显变化;③等效应力的降低是由于压应力的减小而造成的;④参数R1的增大，可积极优化最大压应力值，但是对拉应力并无作用。

综合考虑减少应力和对流道的影响，最终选取R1=7mm的倒圆半径，使整个叶轮的最大等效应力与压应力都有显著的降低。但是R1参数的考虑还不能完全达到叶轮强度要求。

3.3 进口倒角R3对应力影响的分析

叶轮初始叶轮进口倒角R3 =20mm，现针对该参数计算了R3=15mm，R3=12mm，R3=10mm，R3=8mm，R3=5mm这5种结构的叶轮应力情况，其中R1=7，叶轮其余参数不变，保持一致。图12～图15为R3=15mm时，叶轮的应力分布云图。

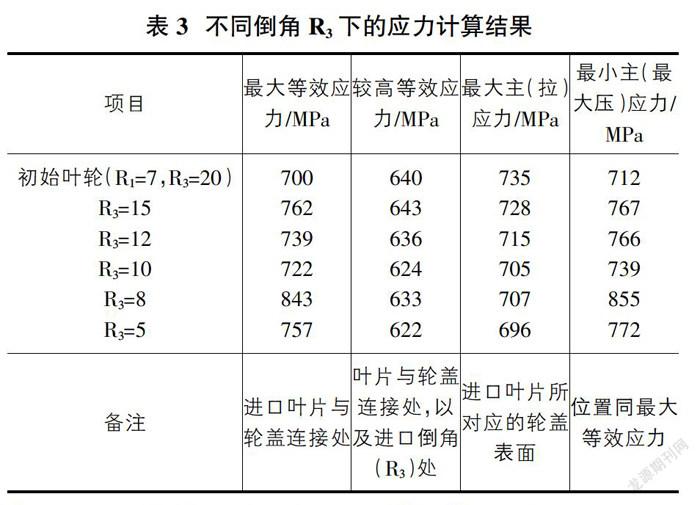
以上不同倒角R3下的应力计算结果见表3。

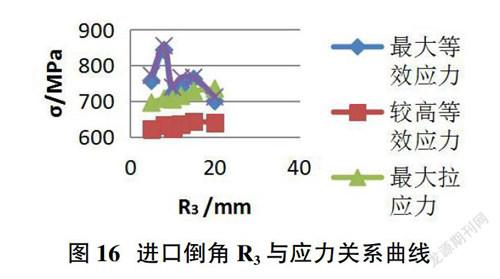
根据表3，整理数据得到以下关于设计参数R3与应力？滓的关系图。（图16）

从以上数据可看出：①随着R3的减小，最大拉应力的数值有减小的趋势，但很缓慢，因此参数R3的为改善拉应力的次要因素，当裕度较大时，可以;②较高等效应力和最大拉应力的变化曲线图相似，且发生区域重合，說明较高等效应力主要由拉应力贡献;③随着参数R3的减小，最大压应力的变化并不呈现规律性变化;④由于最大等效应力主要是由最大压应力贡献，因此最大等效应力与最大压应力的变化曲线类似;⑤参数R3的变化并不能改善叶轮的最大等效应力与最大压应力;⑥参数R3为改善拉应力的次要因素，且改善拉应力后，可能存在使压应力增加的风险，因此在选取参数R3要谨慎考虑。

综合考虑参数R3对拉应力与压应力的影响，最终选取R3=10mm的倒圆半径，均衡了最大拉应力与压应力值。但是R3参数的考虑还不能完全达到叶轮强度要求。

3.4 轮盖倒角R2对应力影响的分析

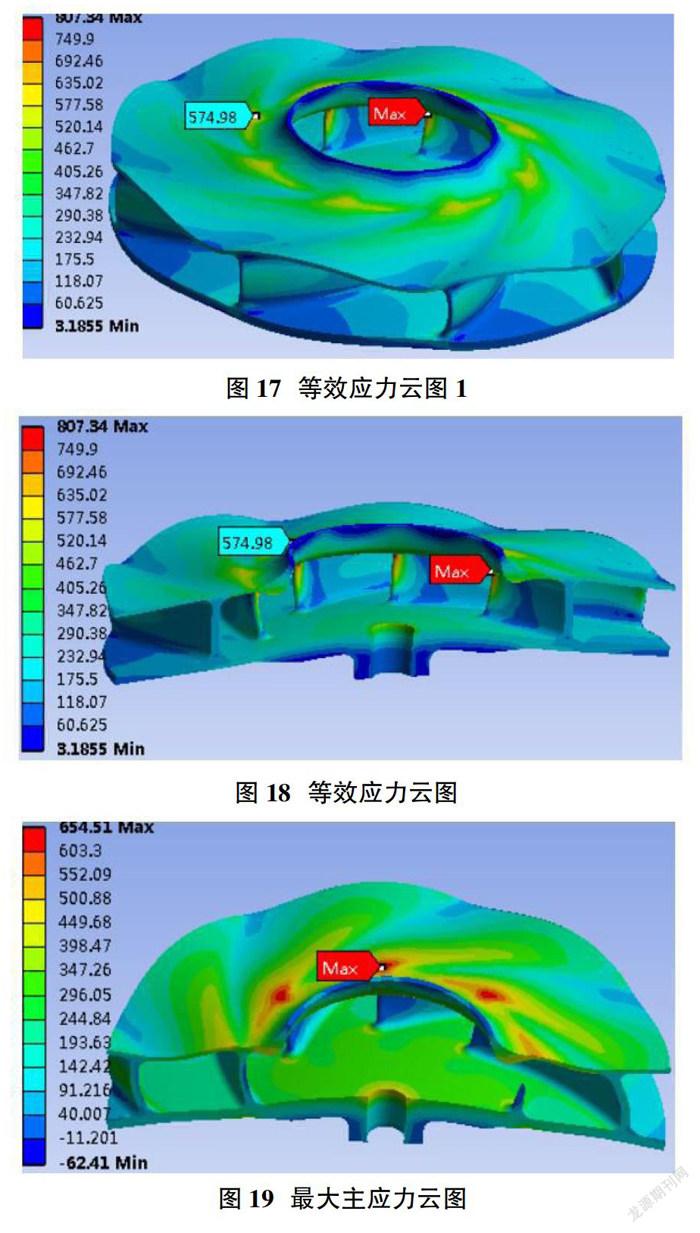
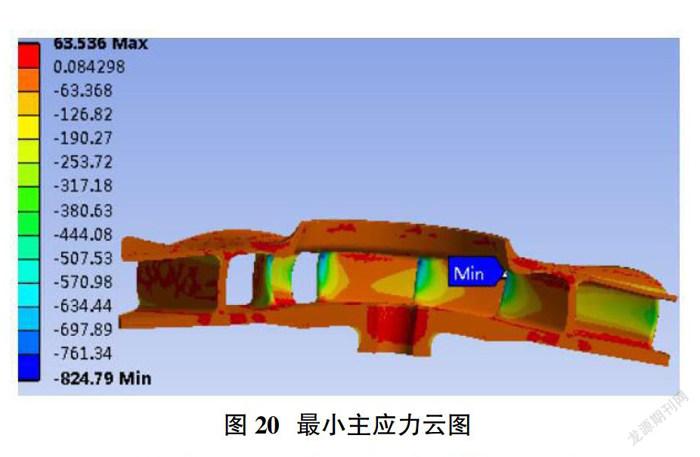
叶轮初始轮盖倒角R2=20mm，现针对该参数计算了R2=25mm，R2=30mm，R2=35mm，R2=40mm，R2=45mm这5种结构的叶轮应力情况，其中R1=7mm，R3=10mm，叶轮其余参数不变，保持一致。图17～图20为R2=25mm时，叶轮的应力分布云图。

以上不同倒角R2下的应力计算结果见表3。

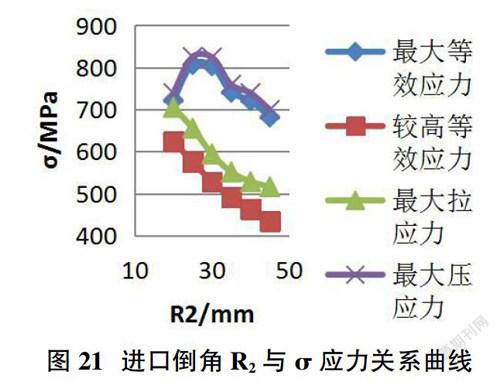
根据表4，整理数据得到以下关于设计参数R2与应力？滓的关系图。

从以上数据可看出：①随着参数R2的增加，最大拉应力减小，并且从应力减小程度来看，参数R2的变化对强度产生的影响较大，可减小27%，因此在设计叶轮的轮背结构时要重点考虑参数R2;②较高等效应力和最大拉应力的变化曲线图相似，且发生区域重合，说明较高等效应力主要由拉应力贡献;③随着参数R2的增加，最大压应力先增大后减小，且由于最大等效应力主要由最大压应力贡献，因此最大等效应力的关系曲线类似于最大压应力;④参数R2有一个最坏值（约为28mm），因此在优化时R2应避开28mm。

综合考虑参数R2对拉应力与压应力的影响，最终选取R2=45mm的倒圆半径，均降低了最大拉应力与压应力值。但是R2参数的考虑还不能完全达到叶轮强度要求。

3.5 轮盖厚度D对应力影响的分析

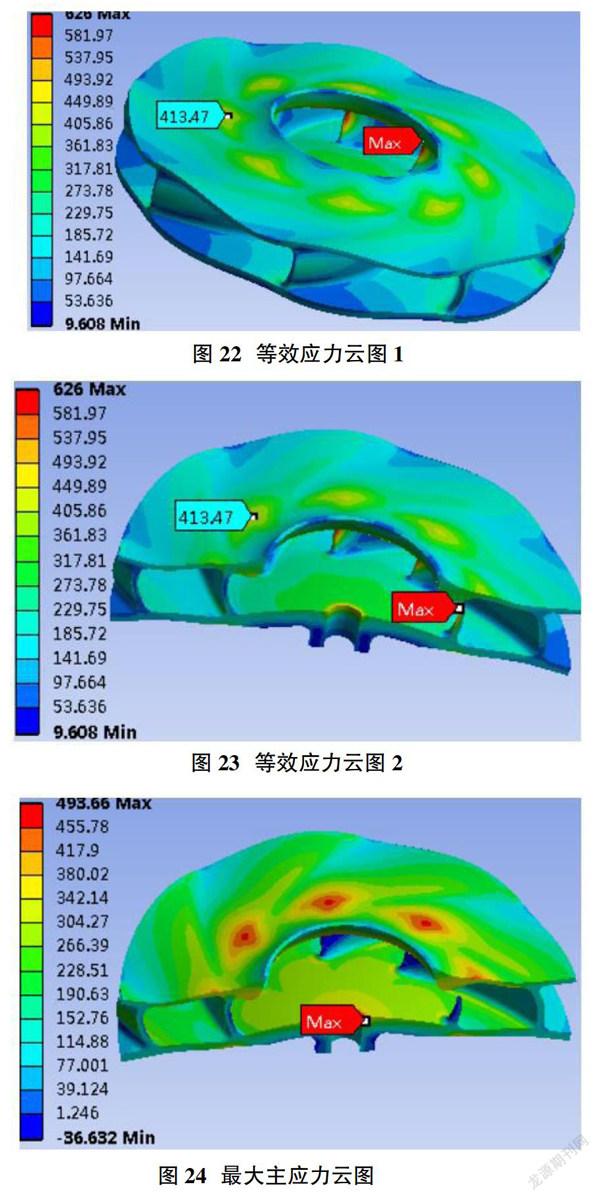
叶轮初始轮盖厚度D =3.5mm，现针对该参数计算了D=5mm，D=7mm，D=8mm，D=9mm，D=11mm，D=13mm这7种结构的叶轮应力情况，其中R1=7mm，R3=10mm，R2=45mm，叶轮其余参数不变，保持一致。图22～图25为D=5mm时，叶轮的应力分布云图。

以上不同厚度D下的应力计算结果见表5。

根据表5，整理数据得到以下关于设计参数D与应力？滓的关系图。（图26）

从以上数据可看出：①随着参数D的增加，最大拉应力先减小后增加，并且从应力减小程度来看，参数D的变化对叶轮受拉强度产生的影响较小;②随着参数D的增加，最大压应力减小，并且从应力减小程度来看，参数D的变化对叶轮受压强度产生的影响较大，可减小32%的压应力;③随着参数D的增加，最大等效应力先减小后增大，分析可知最大等效应力在低谷之前的数值主要由最大压应力决定，低谷之后的最大等效应力值主要由最大拉应力决定;④随着参数D的增加，较高等效应力减小，可知此处的较高等效应力值主要由压应力决定;⑤最大等效应力的数值主要由最大拉应力或最大压应力决定（由数值大的那个决定）。综合考虑参数D对拉应力与压应力的影响，最终选取D=9mm的轮盖厚度，均降低了最大压应力与等效应力值。但是D参数的考虑仍不能完全达到叶轮强度要求。

4  结论

闭式叶轮的进口倒圆处、轮盖（轮背）与叶片交接处、叶片进口处均为叶轮的高应力区。

随着设计参数R1的增加，可大幅度降低叶轮的最大压应力，而最大拉应力并未受影响。

随着設计参数R2的增加，可大幅度降低叶轮的最大拉应力，而最大压应力先增加后减小，因此设计时需要参数R2的避开“最差解”28mm。

随着设计参数R3的减小，可适当降低叶轮的最大拉应力，但趋势很小，因此在裕度足够时可以不考虑优化参数R3。

随着设计参数D的增加，可大幅度降低叶轮的最大压应力，而最大拉应力会先减小后增加，因此在设计是需综合考虑拉应力与压应力值，选取适当的轮盖厚度D。

本文所说的闭式叶轮优化最终采用R1=7mm，R2=45mm，R3=10mm，D=9mm这组优化参数作为最后的设计参数，求解出的最大等效应力值为527MPa。虽通过叶轮外部几何结构设计无法完全缓解叶轮应力集中现象，但在叶轮材料的选择方面存在很大的提升空间。根据软件计算结果，可以方便快速地实现叶轮强度分析，该分析和改进方向可以推广到其他类似叶轮强度分析。

参考文献：

[1]张冲，沈伟涛，张琦，马保伟，李浩.大型离心压缩机叶片热成形回弹研究[J].塑性工程学报，2019，26（05）：51-56.

[2]于博伕.离心压缩机的振动与改进[J].内燃机与配件，2019（21）：242-243.

[3]陈嘉良.离心式压缩机的典型故障研究[J].化工管理，2019（25）：152-153.

[4]尹永伟.离心式压缩机故障原因分析及处理措施[J].化工管理，2019（25）：176-177.

[5]Engineering - Power Engineering; Data from Southwest Research Institute Advance Knowledge in Power Engineering （Experimental Validation of a Wide-range Centrifugal Compressor Stage for Supercritical Co2 Power Cycles）[J]. Energy Weekly News， 2019.

[6]arsan A， Trébinjac S. Coste，G. Leroy. Temporal behaviour of a corner separation in a radial vaned diffuser of a centrifugal compressor operating near surge[J]. Journal of Thermal Science， 2013， 22（6）.

[7]Yutaka Ohta，Yasuhiko Okutsu，Takashi Goto，Eisuke Outa. Aerodynamic performance and noise characteristics of a centrifugal compressor with modified vaned diffusers[J].  Journal of Thermal Science， 2006， 15（4）.

[8]JAPIKSE D， BAINES N C. Introduction to turbomachinery [M]. Concepts NREC， 1997.

[9]张虹，朝臣.车用涡轮增压器压气机叶轮强度计算与分析 [J].内燃机工程，2007，2008（1）：62-66.