基于ARIMA模型的中国猪肉价格预测

张莹莹

摘 要：随着猪肉供给量与消费量的逐年上涨，猪肉价格波动不仅对市场造成了很大的经济影响，还对城乡居民的日常生活造成了很大冲击。猪肉价格的涨跌是一种极易扭曲市场价格的信号，因此本文基于2013年1月—2019年1月的猪肉价格月度数据，建立了基于ARIMA的短期猪肉价格预测模型。应用序列的自相关函数及偏自相关函数序列对2019年2月—2019年4月猪肉平均价格进行预测，得到每斤猪肉分别为29.92元、37.63元、40.09元。然后，从误差均方根、绝对误差平均和Theil不等系数三个方面对ARIMA（3，1，2）模型的预测效果进行评价，得到了良好的预测效果。该预测数据为市场上猪肉的宏观调控起到一定的指导作用，防止猪肉价格大涨大跌对人民生产生活带来巨大的负面影响，并提出健全猪肉价格、做好猪肉供给准备等相关政策性建议。

关键词：ARIMA模型  价格  预测

中图分类号：F714 文献标识码：A

1 背景

近年来，中国人均对猪肉的消费占比始终在75%以上。尽管我国对牛羊肉等替代产品肉类的消费有所上升，但中国居民人均对牛羊肉的消费始终不及猪肉的1/4。鉴于猪肉消费的重要性，猪肉价格变动一直是生产者和消费者密切关注的重点，猪肉市场的供给情况也是农业部门重点监控对象。自2007年起，猪肉价格开始剧烈波动，猪肉价格的涨跌更替对市场的影响是直接且剧烈的。猪肉价格频繁的涨跌对生猪养殖产业带来极大的挑战。当猪肉供大于求时，猪肉过剩，价格下跌，使养殖户承受了巨大的经济损失;当猪肉供不应求时，短期内会使猪肉市场发生膨胀，猪肉价格快速上涨，养殖户获得暴利后会扩大养殖规模。

针对猪肉价格波动趋势的研究，曙光等（2008）采用谱分析的方法测定北京市猪肉价格的季节波动情形，并通过Tukey-Hanning窗谱估计法来预估长期猪肉价格波动，其认为猪肉价格将围绕31个月形成周期波动。同是研究北京市猪肉价格波动规律，于少东（2012）利用X12季节调整法和H-P滤波法对猪肉价格月度数据进行分析，得出北京市猪肉价格短期内波动剧烈，长期波动周期可能是3年的结论。夏海峰（2016）利用数据挖掘中的关联规则理念，在去除异常数据以后，结合二维时间序列对每日的猪肉价格进行预测，预测精度达到89.33%。郭刚奇（2017）基于ARCH模型探究短期市场的猪肉价格波动机制，并总结猪肉价格波动的特征之一就是簇集性明显，短期内猪肉价格极易受外部冲击如疫病等的影响。李子涵等（2019）收集2010年1月—2019年2月的上海市猪肉价格数据，建立ARIMA（p，d，q）模型对未来5个月的猪肉价格进行预测，得出猪肉价格仍将小幅度上涨的结论。罗创国、吴静婷在ARIMA模型的基础上对中国生猪价格以及有代表性的畜产品进行预测，均取得较好的效果。经过对传统ARIMA模型加以改善，吴培（2019）选择运用ARIMA-GM-RBF组合模型对中国猪肉价格进行预测，对每个单一模型进行优缺互补，最后在2011—2018年数据的基础上预测2019年上半年猪肉价格将继续上涨。综上所述，国内学者对猪肉价格的研究取得了不菲的成果。他们对猪肉价格的研究所选取的时间跨度不尽相同，分别对每日、每月、每季度的猪肉价格进行研究，考虑到猪肉价格受到外部因素冲击的影响力度较大，主要进行短期内的猪肉价格预测。猪肉价格的波动不仅影响着猪肉产业链的健康发展，也对人民生产生活和整体经济运行产生重要影响。因此如何准确地预测猪肉价格的波动趋势，是本文研究的重点。基于此，本文将建立ARIMA（p，d，q）模型的猪肉价格预测，通过对猪肉价格的合理预测为市场各经济主体提供有效的理论指导，同时减少对生猪养殖户造成的收益损失，为市场上猪肉价格的宏观调控提供借鉴和参考。

2 ARIMA模型

1970年，博克思和詹金斯提出了一种时间序列预测方法，即差分自回归滑动平均模型又称ARIMA模型。该算法的工作原理是通过多次差分使非平稳序列转变为白噪声序列，充分运用变量的历史信息寻求变化规律，以达到准确预测的目标。该模型多用于农产品和畜产品的价格预测，且实现效果良好。

ARIMA模型构建的基础是ARMA模型，一般形式为ARMA（p，q）模型：

ARMA模型需要保持序列是平稳的，即模型的均值、方差不随时间的改变而改变。但大多经济数据都与时间紧密相关，因此需要对原始数据进行差分以消除长期趋势。若原序列经过d次差分之后平稳，即，则：

是平稳序列，即，因此可以对建立ARMA（p，q）模型：

原ARMA（p，q）模型是非平稳时间序列，在d阶差分后变为平稳，即ARIMA（p，d，q）模型。ARIMA模型将预测对象随时间的变化而形成数据流视为随机序列，通过该模型就可以利用随机序列的历史值来预测未来值。

其中，p表示因变量自身滞后的阶数（AR项），d表示使数据变得平稳的差分阶数，即表示对作d次差分，q表示誤差项的滞后阶数（MA项）。

3 基于ARIMA模型的实证分析

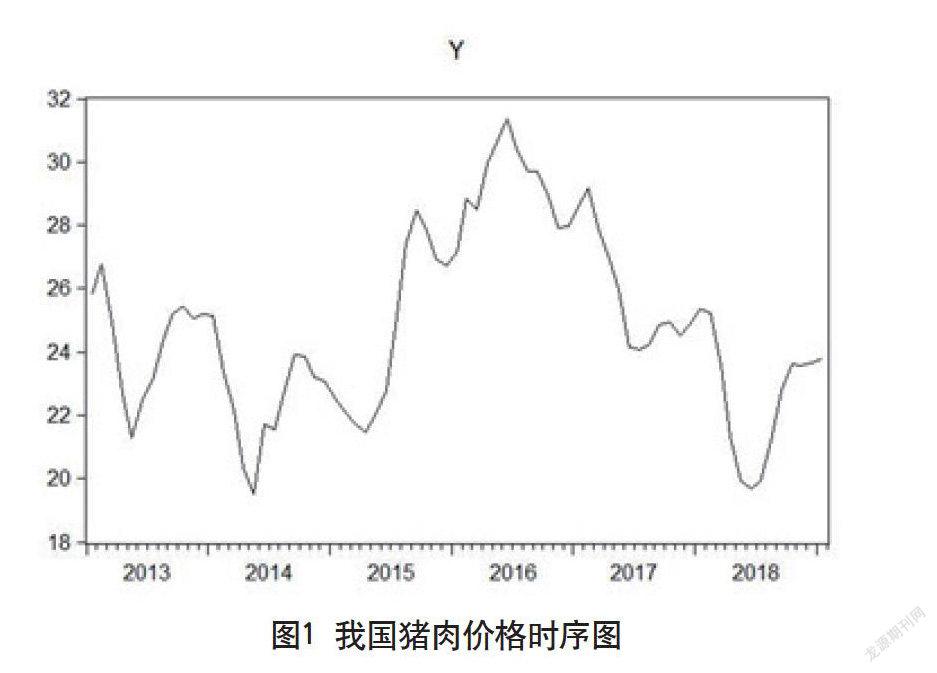
本文选取中华人民共和国农业农村部2013年1月—2019年5月的中国猪肉、羊肉和牛肉价格月度时间序列数据，并通过Eviews9.0软件完成模型计算。近年来，我国猪肉平均价格波动较大，呈现出“跌—涨—跌—涨”的趋势，波动大致呈现出“W”的形状，猪肉价格波动趋势图，如图1所示。

为消除原数据异方差性对模型的建立造成影响，需要对猪肉价格提取自然对数。

图1 我国猪肉价格时序图

采用单位根检验方法对取对数后的国内猪肉平均价格进行单位根检验。猪肉价格序列的ADF检验统计量的值均大于它在1%和5%检验水平下的t统计量的临界值。由此可知，该价格序列存在单位根，是不平稳的。为使原序列变为平稳序列，对变量进行一阶差分处理，结果ADF统计量的p值小于0.05，表明在经过差分后的原价格序列是一阶单整序列，服从。

序列的自相关函数及偏自相关函数序列都是拖尾序列的，P值均小于0.05，说明处理后的数据为非白噪声序列且明显存在相关性。的自相关函数在1阶时明显显著，但第2阶开始骤然下降，其后数值又开始变大，因此可以先设定q值为1。与此同时，的偏自相关函数第1阶显著，也从第2阶开始下降，但是下降幅度不显著，从第5阶起出现明显的下降，因此可以暂时设定p值为2。于是对于一阶差分后的序列，我们初步建立了ARMA （2，1，1）模型。

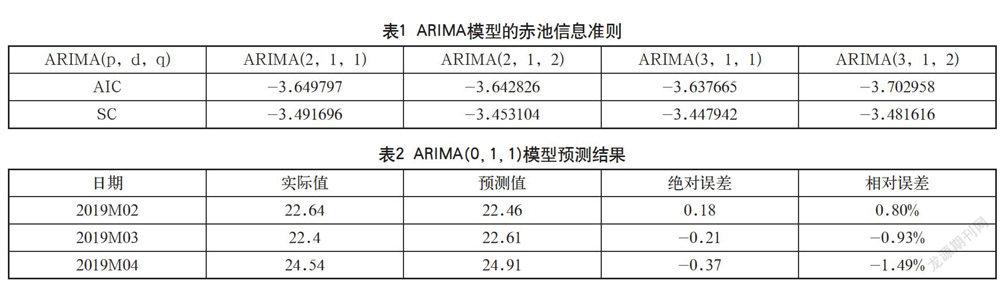
为了更好地优化模型，做到更精准的预测，可以适当增加模型的滞后长度，并根据赤池信息准则确定最终设置的模型，结果如表1所示。

由表1可知，根据AIC和SC信息值，本文选择p=3、q=2建立最终的模型ARIMA（3，1，2）。

对预先设定的ARIMA模型采用线性最小二乘法预测，预测点数为3，得到的猪肉价格如表2所示。

其中，绝对误差=实际值-预测值，相对误差=绝对误差/预测值。由表2计算可得，平均绝对误差为-1.68，平均相对误差为-0.54%，预测精度良好，可以接受。

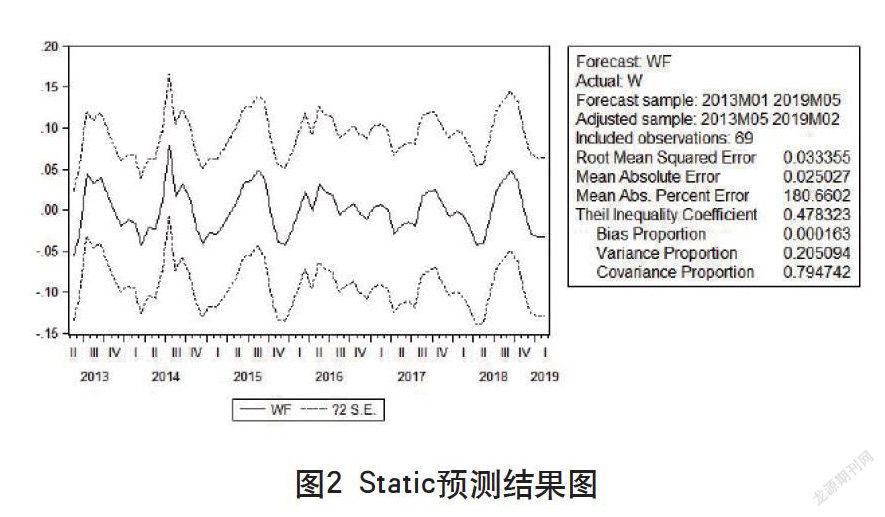
本文采用Static方法来估计2013年1月—2019年5月的，根据结果可观察到整体预测的价格波动区间较小，预测价格的波幅较为自然。假设模型的样本容量为N，需要预测的样本量为n。其中，猪肉价格在t期的真实值为，预测值为，可以通过建立误差均方根、绝对误差平均以及Theil不等系数三个指标对ARIMA（3，1，2）模型的预测效果进行评价，具体如下。

誤差均方根、绝对误差平均以及Theil不等系数指标的数值均证明构建的ARIMA（3，1，2）模型，预测结果如图2所示。 Static预测结果理想，具有准确的精度，可以在实际生产生活中进行运用。

4 结语

本文首先分析整理大量数据，对近年来我国居民人均肉类消费数量及结构进行分析，发现猪肉基本垄断我国肉类市场。在猪肉市场份额占比减少时，其替代产品如牛肉、羊肉等其他肉质产品的市场占比就会增加。

继而以2013年1月—2019年1月的全国猪肉平均价格月度数据为基础，建立ARIMA（3，1，2）模型进行预测分析，得出的结果是2019年2—4月我国每公斤猪肉平均价格分别为29.92元、37.63元、40.09元。预测结果普遍比真实值要大，但是模型的精度较好，预测出短期内猪肉价格波动呈现上涨趋势，符合客观事实。

由于ARIMA模型的被解释变量为滞后变量，非常适合进行价格的预测。本文所建立的ARIMA（p，d，q）一般模型可以便于价格信息使用者快速、简便地掌握价格变动趋势，不仅适用于对猪肉价格的预测，还适用于其他肉质产品及农业产品的价格预测，具有较强普适性。

参考文献

罗增海，王青.近年来猪肉价格波动的研究与思考[J].中国畜牧杂志，2007（22）.

曙光，乔光华.猪肉价格波动周期实证分析[J].北方经济，2008（16）.

于少东.北京市猪肉价格波动周期分析[J].农业经济问题，2012，33（02）.

高铁梅.计量经济分析方法与建模：EViews应用及实例[M].北京：清华大学出版社，2009.