溶质的质量分数题型归纳

洪兹田

溶质的质量分数的相关计算是每年中考的热点，主要包括基础小计算和综合大计算两种类型，现针对这两种类型举例分析如下。

一、基础小计算

溶质的质量分数的基础计算包括：利用溶质的质量分数公式进行溶质、溶剂、溶液的互算;溶液的稀释和浓缩的计算;结合配制一定溶质的质量分数溶液实验的计算;结合溶解度的溶质的质量分数的计算等。

例1（2019·浙江·湖州）配制500 g7.3%的稀盐酸，需要36.5%的浓盐酸 g。

解析：500 g×7.3% = m（浓）×36.5%，解得m（浓） =  = 100 g。

答案：100

点评：根据溶液稀释过程中溶质的质量不变，即m（浓）·w（浓） = m（稀）·w（稀），可求出相关未知量。

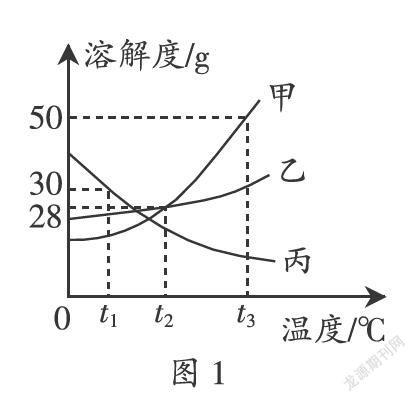
例2（2019·山东·菏泽）溶液与人们的生产生活密切相关，图1为甲、乙、丙三种固体物质的溶解度曲线。

（1）t1℃时甲、乙、丙三种物质的溶解度由大到小的顺序是 。

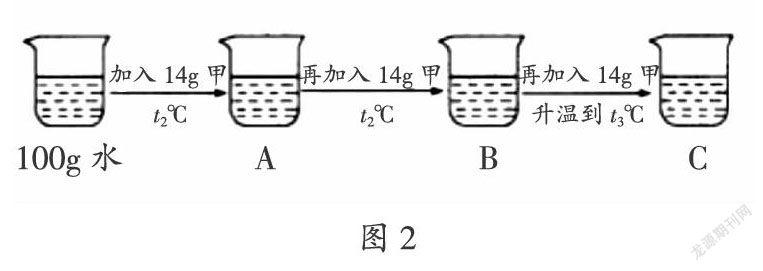
（2）某同学按图2所示进行实验，得到相应温度下的A、B、C三种溶液，其中属于饱和溶液的是

（填字母）。

（3）t3℃时向盛有40 g甲物质的烧杯中加入50 g水充分溶解后，所得溶液溶质的质量分数为

。（结果精确到0.1%）

解析：（1）由溶解度曲线可知，在t1℃时甲、乙、丙三种物质的溶解度由大到小的顺序是：丙>乙>甲;（2）t2℃时甲物质的溶解度是28 g，即100 g水中最多可溶解28 g甲物质，所以B溶液是饱和溶液;t3℃时甲物质的溶解度是50 g，即100 g水中最多可溶解50 g甲物质，C溶液中含有溶质的质量是42 g，所以C溶液是不饱和溶液;（3）t3℃时甲物质的溶解度是50 g，50 g水中最多可溶解25 g甲物质，所得溶液溶质的质量分数为：×100% ≈ 33.3%。

答案：（1）丙>乙>甲 （2）B （3）33.3%

点评：本题综合考查了溶解度曲线的意义以及溶质的质量分数公式的计算，熟练掌握相应知识是解决本题的关键。

二、综合大计算

综合大计算通常涉及与化学方程式结合的综合计算。在溶液中进行的反应，往往是其中的溶质参加反应，所以在根据化学方程式列出有关反应物、生成物的质量比时，要用溶质的质量列比例，而不能直接用溶液的质量或体积列比例。

例3（2019·贵州·黔西南）为测定某氧化铜和铜的固体混合物中氧化铜的质量分数，小勇同学取20 g固体混合物置于烧杯中，将100 g稀硫酸分为四等份依次加入其中进行实验，测得数据如下，回答下列问题：

（1）原固体混合物中，氧化铜的质量分数为 。

（2）上表中，a的值为 ，实验③所得溶液中的溶质是 （填化学式）。

（3）计算该实验所用稀硫酸中溶质的质量分数。（写出计算过程，结果精确到0.1%）

解析：根据第一次固体减少4 g，而第三次后質量不变，说明第二次也减少4 g，所以a = 12。第三次氧化铜完全反应，剩余的10 g为铜单质，所以氧化铜的质量为：20 g - 10 g = 10 g，原固体混合物中，氧化铜的质量分数为：×100%=50%。实验③中稀硫酸过量，所以所得溶液中的溶质是剩余的稀硫酸和生成的硫酸铜，对应的化学式为：H2SO4、CuSO4。根据25 g稀硫酸与4 g氧化铜完全反应可求稀硫酸中溶质的质量分数，设该实验所用稀硫酸中溶质的质量分数为x，

CuO + H2SO4  CuSO4 + H2O

  80        98

  4 g    25 g × x

=

解得x = 19.6%

答案：（1）50% （2）12 H2SO4、CuSO4 （3）19.6%

点评：根据化学方程式计算时，第一要正确书写化学方程式，第二要使用正确的数据，第三计算过程要完整。