浅谈比较策略在小学数学课堂中的应用
鲍华锋
摘要:观察、实验、综合、分析、归纳、比较和抽象等都是研究数学问题的基本方法,而比较策略中的对比、类比等,在数学教学中起着非常重要的作用,应用十分广泛。教师在教学中如果能善用比较方法,识“同” 辨“异”,就能帮助学生更加有效地认识所要研究的对象,把握它们的特征和联系,达到理解、掌握知识,发展思维能力的目的。
关键词:小学数学 比较法 新旧联系
陶行知先生认为,教育的本质是培养具有综合能力的高素质人才。基于这一观点,小学数学教育应该通过各种手段,实现学生多项能力的培养。人们在生活中对客观事物的认识可以说时刻都离不开比较。但是,一个人能比较两个相似的东西,如橡树和槐树、寺院与教堂,即使能知其相似,我们也不能说他有很强的比较能力。我们要求的是能看出异中之同和同中之异。数学教学内容当中,许多知识既相互联系又有区别,只有通过比较,才能在表面上差异极大的对象中识“同”,或在表面上相同或相似的对象中辨“异”。在教学中,我们应该引导学生运用比较策略去学习知识,让学生在比较中有所思、有所悟、有所发现。这样可以使他们更快地习得新知识,更加清晰地了解事物的本质特征,加深对已有知识的理解,更好地掌握重点,突破难点,防止出现混淆和断层现象。这样既可以帮助他们了解知识间的层次性、联系性,同时也可以提高学生的辨别能力,发展学生的思维。下面我就结合自己的教学实践,谈一下在这方面的尝试。
一、比较策略在教学中的运用
1.概念教学中的比较
《数学课程标准》明确指出:“正确理解数学概念是掌握数学知识的前提。”概念是思维的“细胞”,是事物本质属性的反映,是逻辑推理的依据,是学习、掌握知识的基础,也是正确、快速运算的基本保障。对小学生来说,概念描述往往比较抽象,他们学习难度较大。教师可以利用概念间的联系与区别,引导学生进行适当的比较。
(1)在引入新概念时运用比较策略,让学生明确新旧概念之间的差异和关联,为准确理解、掌握新概念打下坚实的基础。
(2)在巩固概念时运用比较策略,可以使学生对新学的概念与易混淆的相关概念进行剖析。例如,对于“减少到”与“减少了”“除尽”与“整除”等看起来差异较小、实际上意义差异较大的相关术语、概念,就可以引导学生进行比较,明确它们的异同。这样不仅能加深学生对相关概念的理解,而且还能达到正确理解实质的目的,有利于培养学生思维的严谨性。
(3)在应用概念时进行比较,可以更“入木三分”,使学生深刻地理解概念的含义,提升思维层次。
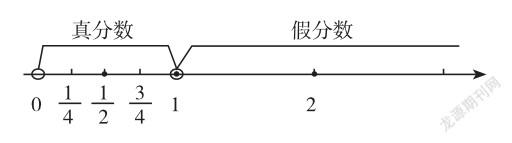
例如,在六年级《数的认识整理与复习》教学中,教师让学生想一个含有2的数,将并其在数轴上表示出来。然后,教师出示學生作品。“看到这个点2,你联想到哪类数?能在数轴上表示出这类数吗?你还能告诉同学们关于这类数的哪些知识?”几个开放的问题启发了学生的思考,通过将数轴作为具体的“支撑体”,学生不仅回顾了关于“数”的知识点,也很容易地联想到自然数、整数、正数、负数、奇数、偶数、质数、合数等。同时,学生通过不同类数的特征比较,深化了认识,也更加明确了它们之间的联系。
2.计算教学中的比较
计算教学在数学教学中占有相当大的比重,也是学生错误比较集中的地方。由于缺乏兴趣、算理不清、计算定律较为相似等原因,学生常会张冠李戴,不恰当地使用计算定律,导致计算错误率非常高。对此,我们可以用比较法提醒学生应该注意的地方,帮助学生发现联系与区别,进一步加深其对算理的理解。
课例:三年级下《两位数乘两位数的笔算(不进位)》的教学中,教师通过对正误两题进行对比,引导学生比较两题的计算方法,询问学生有什么发现。
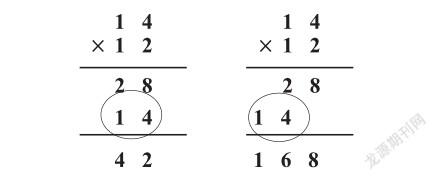
教师引导学生比较两种算法,学生通过估算很快发现,14与12的乘积肯定大于100,而42这个数字太小了。然后学生通过比较两题的不同之处,发现14与十位上的1相乘,结果应该是140,而第一种方法中,后面的0被省略了。这是一道“承上启下”的典型乘法笔算题,也是两位数乘两位数教学中学生最容易错误的地方。通过正误对比,学生不仅清楚了怎么做,而且把为什么这样做也理解透了,为后续的笔算教学打下了扎实的基础,比较的作用不可磨灭。
3.解决问题教学中的比较
解决问题教学中充分运用比较策略,能使学生在比较中理清数量关系,掌握解题方法,形成应用意识,更有利于培养学生的分析和解决问题能力。
(1)单一与复杂问题比较:复杂关系问题都是由几个相关的单一问题组合而成。我们在解决复杂问题的过程中,先让学生回顾相关的单一关系问题,然后引导学生将单一关系问题合并成复杂关系问题,再对比它们的联系与区别。这样学生可以很自然地把握解答复杂关系问题的关键,清晰地发现数量关系,有效地提高解决实际问题的能力。
(2)互逆关系问题比较:比较互逆关系问题的不同解题方法,明确其中的联系,异中比同。这样能让一些零碎的知识点连成串、结成网、形成面,从而建构完整的知识结构体系。
(3)多变题型比较:很多题型可以“一题多解”“一题多编”。运用比较策略,学生的思维在“变”中得到训练,他们可以找出最佳的解题方法,对教学产生兴趣,避免定式思维,提高思维的灵活性、敏捷性。
二、比较策略在教学中的促进作用
1.新旧联系,比中出新
新课标提出“数学知识的教学,要注重知识的‘生长点’和‘延伸点’”。数学知识系统性、逻辑性强,新旧知识联系紧密,后面的知识往往是前面知识的延伸和深化。因此,可以通过复习旧知识自然引出新知,引导学生明确新旧知识之间的区别和联系。学生在分析、比较、判断、推理中构建新知,促进知识的迁移。


2.明确本质,比中明理
小学数学中许多表面相似但实质不同的知识,易使学生产生混淆,成为学生出错的根源。教学中只注重单独教学新知识、概念,忽略不同知识点之间的联系,不对其进行比较,会导致学生只能触及知识肤浅的层面。这就需要加强对“貌似实异”、易混淆的概念的比较,比较它们的异同,弄清楚它们的联系与各自的特点,使学生能够分辨知识的本质属性。同时,消除思维定式带来的影响,排除前后、相关联知识的干扰,更好地把握知识的实质,起到事半功倍的效果。

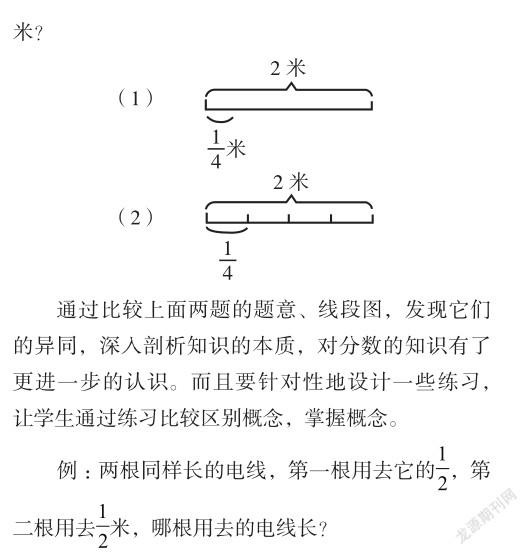
A.第一根 B.第二根 C.一样长 D.无法确定
3.横纵串联,比中入深
数学知识的学习都有着从简单到复杂的过程,仅依靠模仿与练习来学习,学到的知识就会零碎、没有系统性。对于那些隐藏的知识共性,教师可以引导学生在揭示与掌握知识变化的规律性的基础上,运用比较策略,拨开云雾,剥下知识的外层属性,直入问题的核心和本质。这样可以加深学生对数学知识的理解,将各个相对零碎的知识点横连成“线”、纵连成“片”,内化成学生自己的东西,从而逐步建构、完善学生的知识体系,最终达到促进学生智力发展的目的。
例如,六年级《平面图形的周长和面积整理与复习》中,对平行四边形、三角形、梯形等图形的面积计算方法进行比较,发现联系。
师:把平行四边形拉直成长方形后会是什么样子?(平行四边形与长方形比较)
生1:平行四边形的底就变成了长方形的长,高就变成了宽。
师:如果把梯形的上底长度缩小到0后会是什么样子?(梯形与三角形比较)
生2:变成了三角形。这时计算方法就变成了:
(上底+下底)×高÷2=(0+下底)×高÷2=底×高÷2。
师:如果把梯形上底拉成与下底一样长会是什么样子?(梯形与平行四边形比较)
生3:变成了平行四邊形。这时计算方法就变成了:(上底+下底)×高÷2=(底+底)×高÷2=底×2×高÷2 =底×高。
……
师:如果把圆形平均分成若干份,可以拼成哪些近似图形?(圆形与平行四边形、梯形、三角形等比较)
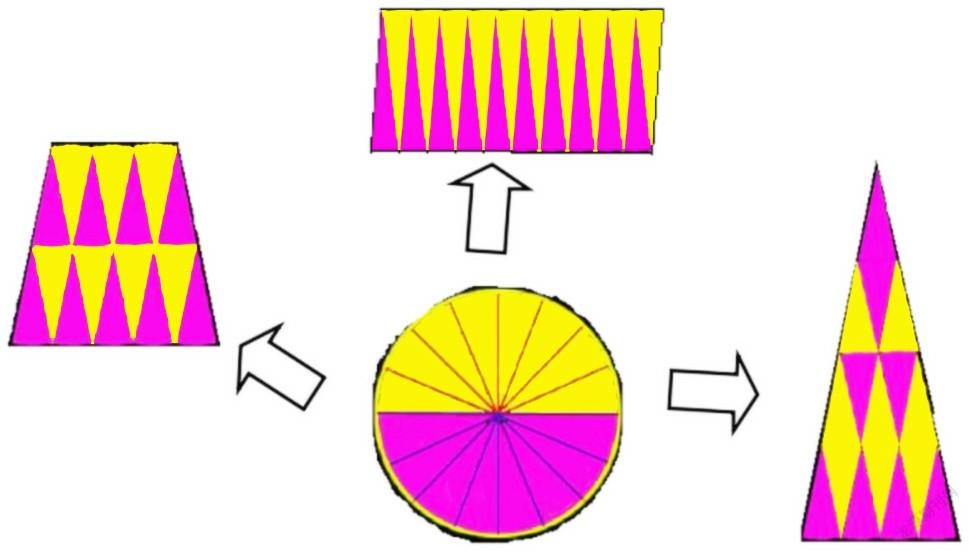
生4:平行四边形、梯形、三角形等。圆周长÷2×高=圆周长÷2×半径=底×高。
……
通过比较,学生不仅把这几个图形的面积计算方法的推导过程有机地联系起来,还在心理上将不同的计算方法统一起来,对这几个图形的计算方法有了更加深刻的理解,对几何图形面积的计算方法有了全新的认识。在课外,还可以让学生比较等差数列求和与梯形面积计算公式的联系。通过比较,学生对知识的本质属性的理解更加透彻;通过比较揭示规律性知识的方法,从某种意义上讲,比新知识与新技能更有价值。
4.多维辨析,比中优化
不同的学生在不同的情境中面对相同的问题时,会产生不同的思维活动,形成不同的解题方法。不同的方法也存在不同思维层次的区别。这时,学生就需要进行全方位、多角度的比较,得出最简便、最符合自身知识建构方式的方法,从而实现优化选择,发展思维能力。
例:一种糖水中,糖与水的质量比是2:13。现在有糖50克,需要加水多少克,才能制成这样的糖水?

……
通过“比”与其他方法的比较,相关知识的特征更加明显、清晰,同时又揭示了比与除法、分数等方法之间的密切联系与区别。学生的思维在比较中得到了锻炼和提升。
有比较才有鉴别。在小学数学教学中适时、恰当地运用比较策略,可以起到事半功倍的效果。比较连接点,促进新旧知识的迁移;比较易混淆点,明晰知识本质;比较联系点,深化理解;比较各种方法,促进优化。通过合理比较,学生能准确、牢固地掌握数学知识,知其然又知其所以然,同时,也提高了分析、鉴别能力,发展了逻辑思维能力。
参考文献
[1]陈茜.例谈比较策略在小学数学中的应用[ J ].基础教育论坛:综合版, 2017(22):12-13.
[2]张婷婷.小学数学阅读指导中比较法的运用策略[ J ].小学教学参考:数学版,2016(5):39.
[3]孙学军. 在比较中孕育数学思维——“比较教学法”在小学数学教学中的应用策略探究[J ].小学教学研究:理论版,2014(11):43-44.

