较低风速下构树叶的热交换效应
苏行健, 陈世辉, 李晶晶, 杨 静, 余雅卓, 万小霞, 尹增芳
(南京林业大学生物与环境学院,江苏 南京 210037)
植物生长的光热环境在一定程度上决定了植物的叶片形状。喜光植物叶片一般较小、较厚、开裂明显且气孔密度较高,而喜阴植物叶片较大、较薄、开裂不明显且气孔密度较低[1-2]。叶片表面温度影响植物的正常生长以及相关生理进程[3-4],叶片本身较薄容易导致局部极端高温,从而引发叶片损伤[5]。叶片的散热和保热能力在维持植物的叶片温度及其正常生长发育中起重要作用,而叶形是影响对流散热的主要因素之一[6]。Andre等[7]认为叶片散热研究的难点主要在于叶片的不规则性和复杂性,即以叶形、叶片表观结构为代表的影响因素的极为不规则性和复杂性,以及蒸腾散热和对流散热的高度耦合。由于研究单个叶片散热的难度较大,大部分的研究工作只能通过对整个冠层或者整株植株进行水热监控来研究其总体散热[8]。应用计算机模拟的方式虽然暂时难以模拟单叶散热,但在冠层或者整株植株的水热交换研究中取得了重要进展[9-13]。
在自然界中,叶片散热时蒸腾散热和对流换热同时进行,难以分离,而且叶片是植物的一部分,受整体其他部分影响,导致植株或冠层的水热交换能力并不等于各个叶片散热能力的简单叠加[9-13]。Gottschlich等[14]和 Vogel[5]利用金属或半导体材料制作模型,对单一叶片散热情况进行了研究,这种人造叶片虽然排除了蒸腾散热的影响,但其物理性质与自然叶片不同。金属模型叶片缺乏自然叶片表面的微观特征以及叶片本身可在风中抖动的特性,而这2种叶片的自然属性均会对散热产生影响[15],因为叶片表面并不是简单的平面,而是具有一定弹性的平面。Morris等[16]的研究结果表明,具有一定弹性或流动性的平面抖动会对平板表面边界层分布产生影响,从而影响散热。因此,将叶片表面当作非弹性平板,可能导致较大误差[15]。Schuepp[1]尝试在叶片表面镀金以保留叶片自身的物理特性,但金属镀层覆盖了叶片的表观结构。Parlange等[15]将叶片裁剪成固定大小,虽然保留了叶片的表观结构,但破坏了叶形的整体性。此外,不同种类植物叶片的形状、大小、微观结构、韧性等存在巨大差异,叶片在对流散热时,复杂且高度耦合的多个因素影响其散热[8],显然不同物种间叶片的散热效果也各不相同。
本研究拟在维持叶片表观生物学特征的基础上,研究叶形对散热的影响,对静止和抖动2种条件下的热交换效果进行测定,同时利用叶片正面和背面表观形态的不同,进一步探究叶片表观结构对散热的影响,以期为解读植物形态特征与生长环境的相关性提供数据资料。
1 材料与方法
1.1 试验材料
本研究选取南京林业大学校园内5年生构树的叶片为试验材料。构树(Broussonetiapapyrifera)属于桑科(Moraceae)构树属(Broussonetia),叶片呈广卵形至长椭圆状卵形,表面粗糙,疏生糙毛,背面密被绒毛,基生叶脉三出,叶片长6~18 cm,宽5~9 cm,先端渐尖,基部心形,两侧常不相等,边缘具有粗锯齿,不分裂或3~5裂,具有明显的异形叶特征。
本试验使用的主要仪器有:迷你风洞(参照李鲁英等[17]的方法自制)、JF-956A恒温加热台(长安金锋电子工具厂产品)、24路无纸温度记录仪(腾辉温控仪表厂产品)、AS852B红外线测温仪(希玛仪器仪表有限公司产品)、手持风速仪(希玛仪器仪表有限公司产品)、叶片扫描仪(EPSON公司产品)、高精度测温仪(希玛仪器仪表有限公司产品)和K型号热电偶探头(希玛仪器仪表有限公司产品)等。
1.2 试验方法
1.2.1 样本制作与筛选 为了减少蒸腾作用对新鲜叶片表面散热能力的影响,保持叶面平整,采集构树叶,参照腊叶标本的操作步骤制作叶片标本。利用叶片扫描仪筛选形状规则、对称,且叶面积为100~110 cm2的叶片。采集自然状态下的心形叶和开裂叶各500片,编号备用。
1.2.2 构树叶片物理特性的检测 用瞬态热线法测定构树叶的导热系数(测试温度20 ℃),使用差示扫描量热法测定构树叶的比热容(测试温度23 ℃),利用K型号热电偶探头和AS852B红外线测温仪测定叶片正面和背面的表面发射率。
1.2.3 测温点的选定 分别以主脉和2条最大的侧脉为轴线设置测温点(图1),测温区域是以测温点为圆心,直径为1.3 cm的圆,注意测温区域不可超出叶面。其中O、A、B、T、G、H点位于主脉上,经测量发现,从O点到T点的主脉温度呈现先上升再下降的趋势,G点和H点分别为心形叶和开裂叶主脉上温度最高的点。

图1 测温点示意图Fig.1 Distribution of the measured points
1.2.4 抖动状态下叶片表面的对流换热系数 使用冷却法测定抖动状态下叶片表面的对流换热系数。将实验室室温稳定在27 ℃,试验过程中风扇保持开启状态,固定叶片在风洞内,叶片主脉的方向与风向平行,叶柄朝向风扇方向,通过调整风扇离风洞的距离保证叶片上方风速为1 m/s。
测温前将微型热电偶探头固定在测温点,再将K型号热电偶探头连接在24路无纸温度记录仪上。同时在叶片正上方5 cm处固定一个温度计来测量空气温度。
用热金属片夹住叶片,对叶片进行均匀加热,叶片略微超过45 ℃后停止加热,然后将金属片迅速移出风洞并让叶片在风速1 m/s的风洞中冷却,在金属片移出风洞的瞬间正式开始测温。测温时,利用K型号热电偶探头记录测温点的温度变化,由24路无纸温度记录仪配套软件的数据管理系统V1.06进行数据处理,最终得到相应的温度变化曲线。测温的同时读取风洞内叶片正上方的空气温度。通过温度变化曲线计算该点的对流换热系数(h)。
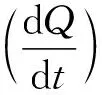

(1)
式中,T0为环境温度;T为系统表面温度;h为常数。
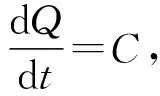
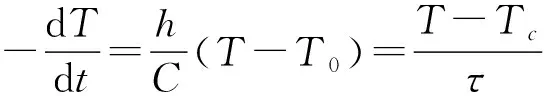
(2)

非稳态散热时叶片内外温度分布均匀是基于经验判断得出的结论,是使用冷却法的前提[5,14]。通过计算毕渥数Bi来验证其正确性。
在非稳态散热情况下,可以有以下规律:

λ(叶片)≈λ(水)×k≈0.6×k
式中,Bi为无量纲物理量;h为气体强制对流条件下的对流换热系数;δ为叶片平均厚度;λ为固体导热系数;k为叶片含水率。已知h:20~100 W/(m·K),δ≈0.000 35 m,k≈60%。
1.2.5 静止状态下叶片表面的对流换热系数 使用热平衡法[5,15]来计算静止状态下叶片表面各测温点的对流换热系数。热平衡是指系统的吸热散热相对平衡,系统各个部分的温度几乎不再变化。通过测量温度以及叶片的热物性[18],再代入物理公式计算出对应点的对流换热系数。这里要注意的是,热稳定不是指叶片表面温度均匀[8],而是热流量的稳定,这也是热平衡法使用的前提。
将1.5 g/L琼脂调成凝胶并倒入浅平板型模具,在琼脂半凝固时将叶片铺平粘在琼脂表面,随后静置。为了防止叶片与琼脂的接触面出现气泡,需提前在接触面均匀涂抹一层琼脂。在琼脂完全凝固后,用解剖刀削去叶片周围多余部分,保持叶片形状,最后将叶子放置于恒温加热台上加热至40 ℃。
加热前调整风扇和风洞的距离,保证叶片上方风速为1 m/s。同时,将叶片放在风洞内的固定位置,以减少不同位置气流状况差异对试验结果的影响。叶片主脉的方向与风向平行,叶柄朝向风扇方向。待装置进入热平衡状态时方可测温。
使用AS852B红外线测温仪测温,测温枪前端与测温点间隔15.0 cm,保证测温区域是一个直径为1.3 cm的圆。同一点重复测量3次,取平均值以减小误差。
叶片表面对流换热系数的计算过程如下:
根据Stefan-Boltzmann定律计算局部热辐射,可以写出该模型叶片的局部能量平衡公式,即
(3)

本试验各个样本与环境的温差基本相同,每组试验辐射换热情况相同,且相比对流散热量很小,所以可以忽略辐射换热的影响。
E=Hd=q·S
(4)
式中,E热传递热量;Hd是通过对流和传递的局部热损失量;q为热流密度;S为叶片表面积。
q可以通过一维稳态传热模型求得:
(5)
式中,q为热流密度;λ为叶片导热系数;δ为叶片平均厚度,δ(构树叶)≈(0.30±0.02) mm;t2为叶片表面温度;t1为琼脂温度;△t为t1与t2间的温差。
(6)
计算出对应的静止状态下叶片表面对流换热系数h。
利用Excel2010、Word2019和SPSS_Statistics_v22.0.0.0软件进行图表制作。
2 结果与分析
2.1 构树叶片的导热系数、比热容和反射率
构树的叶片较薄,叶片内部的导热性能不佳,导致叶片表面温度受环境温度影响较大,叶片表面不同区域之间容易出现较明显的温差[18]。表1显示,构树叶片的导热系数和比热容分别为0.053 7 W/(m·K)和0.120 0 J/(g·℃),而且叶片正面和背面的反射率非常接近,表明叶片正面和背面吸收太阳辐射的能力基本相同。
2.2 叶片正面和背面散热能力的差异
为了探究叶片正面和背面散热能力的差异,即由表观结构不同而造成的散热能力差异,本研究比较了静止状态下叶片正面和背面各个测温点的温度及对流换热系数之间的差异。对流换热系数代表单位时间单位面积系统表面的散热量,即散热速度,能直观表示散热能力。表2显示,心形叶主脉上G点温度最高,开裂叶主脉上H点温度最高。相同叶形叶片背面的对流换热系数总体略高于叶片正面,这可能是因为构树叶片背面有一层短绒毛,导致叶边界层与空气换热的面积增大,从而增强了散热。同时,短绒毛可能在某些程度上使边界层变薄,让对流换热更加容易进行[19]。静止状态下,叶片正面F点和H点的温差为1.9 ℃,E点和F点的温差为0.1 ℃。表3显示,静止状态下开裂叶叶片正面和背面的对流换热系数存在显著差异。

表1 构树叶片导热系数、比热容和反射率
2.3 静止状态下叶形对叶片散热能力的影响
自然生长条件下,大多数叶片的形状并不是严格的轴对称图形,而且叶片的开裂部分还具有一定随机性。由于开裂叶的形状极为复杂,所以叶片表面温度分布不均匀。通过选取具有代表性的位于叶脉上的测温点,比较不同叶形同一位置测温点的对流换热系数,发现开裂叶的叶脉上同一位置测温点的散热能力要高于心形叶(表2),与叶片的边界层理论相符合[19],与从进化角度得出的理论预测结果一致[2,20-21]。
2.4 同一叶片不同部位散热能力的差异
表4显示,静止状态下心形叶不同测温点的对流换热系数存在着显著差异。同时,静止状态下开裂叶不同测温点的对流换热系数也存在着显著差异(表3)。所以,无论是心形叶还是开裂叶,叶片上不同部位的对流散热能力存在显著差异。
表2显示,同一片构树叶上D点和G点的对流换热系数差异较大,这可能是因为风掠过的最初一段短距离内,对流换热系数会发生剧烈的变化[22]。G点和H点的对流换热系数低于其他靠近叶片边缘的测温点。根据叶边界层理论,这主要是因为叶片边缘的边界层与叶片中心相比较薄,边界层越薄,散热能力越强。
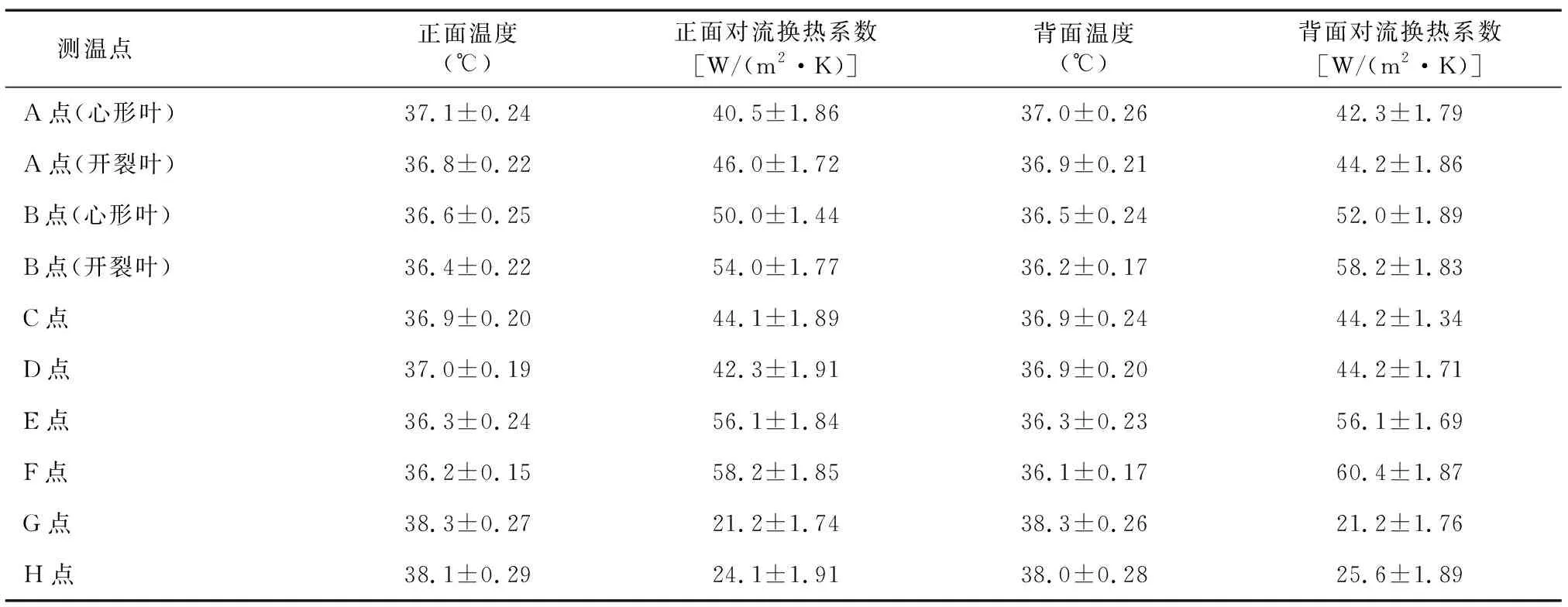
表2 静止状态下叶片正面和背面温度及对流换热系数

表3 静止状态下开裂叶片正面和背面对流换热系数的多因素方差分析
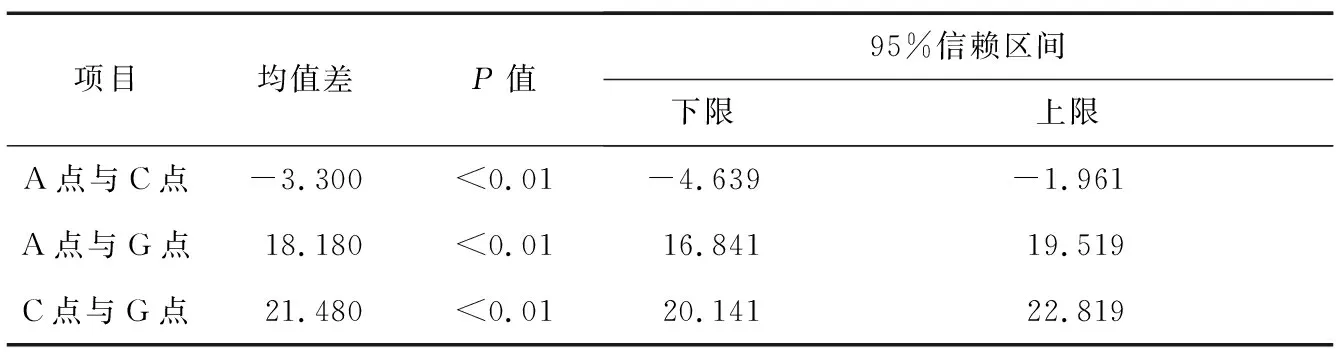
表4 静止状态下心形叶表面不同部位对流换热系数的单因素方差分析
2.5 静止和抖动状态下叶片散热能力的差异
本试验条件为强制对流,所以抖动状态下的散热适用牛顿冷却定律[23-25],即冷却法所得结果准确。表5显示,抖动状态下构树叶的对流换热能力总体高于静止状态下构树叶的对流换热能力。同一叶片上同一测温点,抖动状态下构树叶的对流换热系数约为静止状态下的1.0~1.2倍。本研究的结果与流动平板的散热研究结果一致,即有一定流动性的平板相较于固定平板的对流散热能力有了一定程度的提升[20]。分析抖动对叶片散热能力的增强效应,发现叶片的边缘部位总体高于中心部位。这可能是因为叶片抖动容易扰动叶边缘附近的气流,增加了气流的湍流度,一定程度上提高了叶边缘部位的对流换热能力[1,6,14,26-28]。

表5 抖动状态和静止状态下叶片不同测温点的对流换热系数
2.6 叶截面内部温度均匀的验证
通过方法1.2.4计算,构树叶的非稳态冷却模型中Bi趋近于0,叶片截面内部温度均匀,叶片表面温度可以代表叶片内部温度,即AS852B红外线测温仪可以准确测量叶片温度。
3 讨 论
植物的对流换热能力受多因素影响,叶形是最明显且最重要的影响因素之一。在研究单个叶片散热时,由于影响其散热的因素过于复杂,并且这些影响因素之间高度耦合,相互影响,所以很难将单个影响因素分离出来研究[8]。对叶片散热情况的研究大多数是对冠层或整株植株进行分析[8]。
叶形对叶片散热的影响包括:叶形本身对热交换的影响以及不同叶形的叶片抖动对换热产生的影响。Schuepp[1]尝试使用电化学法研究抖动状态下叶片的散热,但金属镀层覆盖了叶片的表观结构,所以其结果误差较大。Parlange等[15]首次将抖动对叶片散热的影响单独分离出来,但由于破坏了叶形的整体性,且试验在湍流条件下进行,最终导致抖动对散热的影响在试验中难以表现出来。Gottschlich等[14]和Vogel[5]发现开裂叶的对流换热能力较强,与本研究结果一致,但使用人造叶导致试验结论难以推广。当叶形有明显差异时,很难相信叶片的抖动不会受到巨大而复杂的影响,二者紧密耦合,很难分离,导致试验出现漏洞[15]。
为了分离叶形这一影响因子,本研究选取异形叶作为试验材料,保证了试验材料的准确性和均一性。本研究结果表明,与心形叶相比,开裂叶在本试验条件下的对流换热能力更强。
准确而全面地测定叶片温度是解析叶形影响散热机制的重要条件,前人研究多用叶片表面平均温度或者某一点的温度来代表叶片表面温度变化和散热情况[8]。叶片表面温度平均值的差异可以在一定程度上反映散热情况,但叶片表面的总体降温不代表不会出现局部高温的损害。事实上,在复杂多变的自然环境中,叶片较薄的话极有可能导致叶片局部高温[5],这就使叶片表面出现温差,而温差所代表的散热能力差异在过去的试验中没能很好地表现出来。本研究通过使用科学装置,并借助热平衡法,测定叶片表面不同测温点的温度,从而准确、细致地观察到叶片表面温度的分布,为叶片散热机制的解析提供了可靠资料。另外,为了直观地表现叶片表面温差所代表的散热能力差异,直接用对流换热系数来表示对流换热能力,比较叶片换热能力的差异,使用自制的风洞等装置,通过热平衡法和冷却法对叶片表面温度的分布进行研究[15,29-35]。本研究发现,叶面积相近时,即叶片表面气孔数目相近时,开裂的叶形更有利于叶片散热。同一片叶子,越是靠近叶边缘,越是较为狭窄的地方,其散热能力越高[6],这与小叶子的纯物理散热能力更强的理论一致[36]。但是自然界中由于干热导致的叶片干枯主要是从叶片边缘开始的[37],这主要是因为在自然条件下叶片的散热不光有对流换热,还有蒸腾散热。可见,植物异形叶的热交换效应非常复杂,涉及很多外界因素,今后还需要进行更深入的研究。

