一类带位势与散射阻尼半线性波动方程解的破裂

范雄梅， 明 森， 韩 伟

(中北大学 理学院， 山西 太原 030051)

0 引言及主要结论

本文研究外区域上带位势与散射阻尼的半线性波动方程初边值问题

(1)

式中： Ωc=RnB1(0), Ω=B1(0)为Rn中的单位球；μ>0，β>1；ε>0为任意给定的充分小的正数； 位势0≤V(x)≤C(1+|x|2+δ)-1，C>0，δ>0均为常数；μ(1+t)-βut为散射阻尼.

关于带阻尼的线性波动方程的Cauchy 问题

(2)

近来， 带阻尼的非线性波动方程的Cauchy问题受到广泛关注[3-9]. 目前的主要研究结果集中在β∈(-∞,1]. 当β=1，μ=2时， Fujita 指数与Strauss 指数密切相关. 文献[6]研究了次临界指数具散射阻尼的半线性波动方程， 利用试探函数方法和迭代方法得到解会破裂及其生命跨度的上界估计， 但没有涉及位势项和外区域. 而对于问题(1)， 目前还没有相关结果.

本文考虑当空间维数n与非线性项指数p满足一定条件时， 问题(1)的解总会在有限时间内破裂， 进而得到其生命跨度的上界估计. 本文主要结果如下：

定理1设n≥1, 1R>2.f(x),g(x)不恒等于0. 记r(p,n)=2+(n+1)p-(n-1)p2. 设问题(1)的解满足suppu⊂{(x,t)∈Ωc×[0,T)‖x|≤t+R}， 则问题(1)的解u将在有限时间内破裂， 且有如下生命跨度T(ε)的上界估计

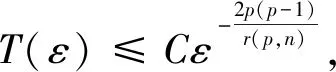
(3)

式中：C是与ε无关的正常数， 0<ε<ε0，ε0=ε0(f,g,p,μ,R).

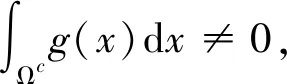
(4)

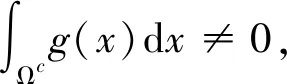
(5)

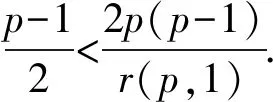
下面给出证明定理1～3时需要用到的引理.

引理1[3，10-12]引入两个试探函数φ0(x),φ1(x)∈C2(Ωc),n≥1， 则有

式中：C0,C1为正常数； 位势0≤V(x)≤C(1+|x|2+δ)-1,C>0,δ>0， 均为常数. 当V=0时， 记r=|x|， 则有

注3本文将文献[6]中所研究的次临界指数带散射阻尼的半线性波动方程小初值问题推广到外区域上带位势的情形， 其中位势0≤V(x)≤C(1+|x|2+δ)-1，C>0，δ>0均为常数. 若问题(1)中V(x)=0， 当n≥4时可取φ0(x)∈(0,1)， 而n≤3时则给出具体径向试探函数φ0(|x|)， 见引理1.

注4利用波动方程的有限传播速度性质知当时间t有限时，r亦有界. 故n=1, 2时，φ0(x)有界.

现记ψ1(x,t)=e-tφ1(x)， 其中φ1(x)如引理1中所述.

引理2[3]设p>1,φ0(x),φ1(x)满足引理1中的条件，n≥1. 则∀t≥0，

式中：C为正常数.

1 定理1的证明

首先， 给出问题(1)弱解的定义.

定义1设u是问题(1)在[0,T)的能量解， 并且

u∈C([0,T),H1(Ωc))∩C1([0,T),L2(Ωc))∩

满足

(6)

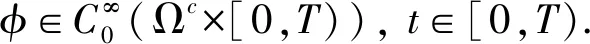
现引入如下函数

其中，u是问题(1)在[0,T)上的解.

记ψ1(x,t)=e-tφ1(x)， 其中φ1(x)如引理1中所述. 引入指数乘子.

m(t)=exp(μ(1-β)-1(1+t)1-β)).

若β>1， 则有

1≥m(t)≥m(0),t≥0.

(7)

下面建立F0(t)的估计. 利用引理1可得

在式(6)中令

φ(x,s)=φ0(x),

(x,s)∈Ωc×[0,t], |x|≤s+R,

得到

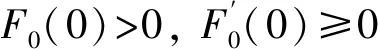
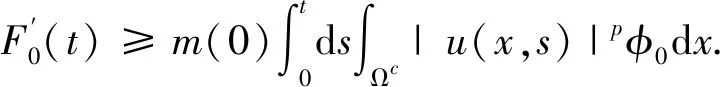
(8)

下面建立F1(t)的下界估计.

运用Holder不等式及引理2， 则有

(9)

其中,C1>0. 令

φ(x,t)=ψ1(x,t)=e-tφ1(x)，

则有φt=-φ,φtt=Δφ. 对式(6)求导， 在方程两边同时乘以m(t)， 并在[0,t]上积分， 则有

利用引理1得到

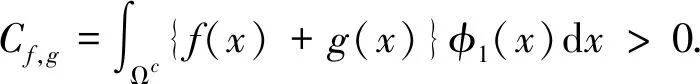
(10)

运用Holder不等式， 得到

(11)

式中：C2>0. 结合式(8)和式(11)， 可得

(12)

式中：C3=C2m(0)>0. 利用式(8)～式(10)， 并在[0,t]上积分得到

(13)

下面利用迭代方法建立问题(1)解的生命跨度T(ε)的上界估计.

首先， 对于t≥0,j∈N*， 假设

F0(t)>Dj(R+t)-ajtbj,

(14)

式中：Dj,aj,bj将在下文中给出其定义， 而且

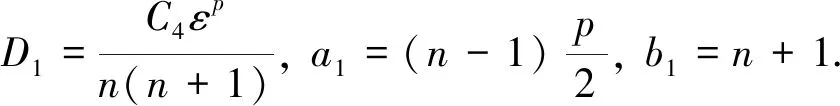
(15)

将(14)代入式(12)中， 得到

现定义序列{Dj}， {aj}， {bj}. 由于

bj+1=pbj+2,

(16)

于是，F0(t)>Dj+1(R+t)-aj+1tbj+1.

利用式(15)和式(16)得到

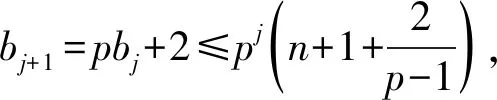
于是

(17)

由t≥1， 可得

其中

若

则有J(t)≥1. 在式(17)中令j→∞， 则有F0(t)→∞. 从而得到生命跨度的上界估计

其中，C7是不依赖于ε的正常数.

2 定理2与定理3的证明

2.1 定理2的证明

F0(t)≥C9ε(R+t),

从而得到定理2中生命跨度的上界估计.

2.2 定理3的证明

结合定理1和定理2的证明过程， 当n=1时， 可知

类似地， 可得

从而可得到定理3中生命跨度的上界估计.