地球卫星星光折射导航量测量及其性能对比
宁晓琳,梁晓钰,孙晓函,王帆,王龙华,房建成
1. 北京航空航天大学 前沿科学技术创新研究院,北京 100083
2. 北京航空航天大学 仪器科学与光电工程学院,北京 100083
地球卫星实现自主导航,一方面可以减轻地面站的负担,在测控系统发生信息阻塞或受到干扰时,提高地球卫星的生存能力;另一方面,可以为自主控制和自主管理等提供支持。天文导航是一种重要的地球卫星自主导航方法[1],而地平测量精度则是影响地球卫星自主天文导航性能的一个重要因素[2]。根据敏感地平方式的不同,地球卫星的自主天文导航可分为直接敏感地平法和利用星光折射间接敏感地平法[3]。直接敏感地平的天文导航方法是利用地球敏感器直接测量地球边缘从而获得地心方向[4],其原理简单易于实现,但是受地球敏感器测量精度的限制,导航精度不高,此外,大气层的覆盖会导致地球边缘位置难以精确确定,也会导致导航精度下降[5]。星光折射间接敏感地平的方法是20世纪80年代初发展起来的一种低成本、高精度卫星自主天文导航方法[6]。该方法利用星敏感器观测被地球大气边缘折射的恒星,从而间接获得地心方向信息,由于现阶段星敏感器的测量精度远高于地球敏感器[1],因此可大大提高导航精度。
早在1960年初,美国Draper实验室(Charles Stark Draper Laboratory,CSDL)在Apollo计划实施之前,就对利用天体掩星、星光大气折射、星光大气衰减等自主导航方案进行了研究[2]。1975年,CSDL研究了星光折射/色散自主导航方案,提出了几种星光折射敏感器的设计方案。CSDL于1979年开展的关于大气星光折射能否提供真实数据的研究是星光折射自主导航方法发展过程中的重要一步。结合地面测控站提供的精确的卫星轨道参数,CSDL利用掌握的2颗NASA卫星(OAO-3和HEAO-2)的高精度在轨观测数据对大气平流层的密度变化量进行了深入分析。1980年,OAO-3卫星成功获取了折射数据,CSDL在研究了许多观测数据后,推断星光折射导航可能获得较高的精度。1984年,CSDL对星光折射自主导航方案进行了误差分析和仿真研究,假定大气折射高度为25 km,以视高度作为观测量,一个轨道周期内观测40次折射星,利用卡尔曼滤波(KF)得到优于100 m的导航精度[7]。20世纪80年代初,法国国家空间研究中心以低轨观测卫星SPOT为研究对象,进行了基于星光折射的自主导航的研究,通过多次平流层气球试验对大气折射的特性进行了研究,预计此方法的导航精度可达300 m[8]。上述关于星光折射自主天文导航技术的研究均为理论研究,一直没有得到实际的应用验证,直到多任务姿态确定和自主导航(Multi-mission Attitude Determination and Autonomous Navigation,MANDAN)系统在空间进行试验才开始得到实际工程应用[9]。
国内关于星光折射自主导航的相关研究一直在开展。1995年,董云峰和章仁为[5]初步研究了利用星敏感器实现卫星自主导航的方法,其中包括利用星光折射实现卫星自主导航的内容。周凤岐等[10]和唐琼[11]对利用星光折射自主天文导航实现卫星自主定轨进行了研究。薛申芳等[12]根据组合大视场星敏感器卫星自主定轨的需要,对组合大视场星敏感器观测的星光折射有关参量进行了研究。王国权等[13]根据卫星、地球和星光折射视高度间的几何关系,建立了星光折射模型,给出了20~60 km视高度范围的星光折射角随星光折射视高度变化的经验公式。胡静和杨博[14]建立了视高度范围为20~50 km的星光折射观测模型,同时进行了仿真研究。Wang和Ma[15]在考虑所有大气折射模型影响因素的基础上,建立了一种更为精确的连续高度(20~50 km)大气折射模型的经验公式。文献[1]系统地研究了星光折射自主导航方法,对导航系统进行了详细的误差影响因素分析,给出了部分可供参考的结论。王海涌等[16]根据视场内平流层条带所占视场面积的比例,建立了折射星数在星敏感器视场内的概率分布模型,并提出了一种星光折射解析定位方法。武鹏飞等[17]进一步对星光大气折射模型进行了研究,利用光线追迹方法,建立了一种考虑大气空间不均匀性的星光大气折射模型,使星光折射导航的理论精度进一步提高。杨博和苗峻[18]等针对星敏感器接收折射光线的过程中,太阳、地气光等杂光造成星图背景增强,使星光折射导航系统观测缺失提出了一种航天器星光折射连续导航方法,该方法利用观测的折射星解算航天器位置的同时建立即时神经网络权值,进入星光空白段时,导航系统通过神经网络补偿算法实现导航延续,该方法下的“空白段”的导航合方向精度误差在10%之内,保证了星光折射导航的精度。
随着星光折射导航理论研究的发展,其在中国得到了大量的应用。近几十年,中国开展近地星光导航技术研究,先后研制出多种星光导航设备,这些设备自动化程度高,可直接输出载体相对于惯性坐标系之间的相对姿态信息,极大的提高了航天器自主导航的性能[19]。随着技术的发展,星光折射导航在舰船自主定位[20]、弹道导弹导航[21]等方面的应用也逐渐发展了起来。
上述研究均以星光折射视高度为量测量,但星光折射视高度存在获取困难、无法反映折射方向信息的不足,针对上述问题,近年来北京航空航天大学先后提出了基于星光折射角[22-23]和折射星像素坐标(折射星矢量)[24]的星光折射导航方法。本文结合星光折射导航的基本原理对这3种量测量的获取方法和量测模型进行了综述,并通过仿真比较了相同条件下3种量测量的导航性能和可观性。仿真结果表明,由于折射星像素坐标(折射星矢量)可以同时反映星光折射的大小和方向,而星光折射角和折射视高度仅能反映星光折射的大小,无法反映其方向,因此折射星像素坐标的导航性能优于星光折射角和折射视高度。此外,还对星敏感器精度、卫星轨道高度、星敏感器安装夹角3种因素对3种方法的性能影响进行了分析。
1 星光折射导航的基本原理和量测量的获取
1.1 星光折射导航的基本原理
星光折射自主导航是利用大气的光学折射特性实现卫星的自主导航,如图1所示,当恒星星光经过地球边缘的大气层时,由于大气密度不均匀且随高度下降而增大,此时,星光会发生折射并朝地心方向弯曲,在这个过程中,星光折射的大小和方向是卫星位置矢量的函数[25]。因此利用星敏感器观测经过大气边缘被大气折射的恒星,能够观测到其星点位置相对未发生折射的恒星发生了明显的变化,如图2所示,其中Nx和Ny表示点在这个图里的位置。利用这一特点可以实现折射星的识别,并根据其折射前后的像素坐标,得到其未折射的真实星光方向S和折射后的视方向Sr,进而得到折射后的视方向与未折射的真实星光方向之间的夹角——星光折射角R。此外,从卫星上观测到的折射光线相对于地球表面的高度为视高度ha,是R和大气模型的函数。大气密度分布决定了星光的折射轨迹,而地球卫星的位置决定了可观测到的折射星和星光折射角R和折射视高度ha的大小。以传统的星光折射导航量测量折射视高度ha为例,由图1所示的几何关系可以得到ha与地球卫星的位置矢量r具有如式(1)所示的函数关系,图中hg为实际折射星光的大气切线高度。

图1 基于星光折射的地球卫星自主导航基本原理

图2 星图
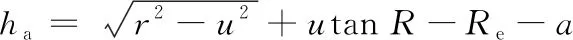
(1)

因此,利用折射星像素坐标(折射星矢量)、星光折射角R和折射视高度ha为观测量,结合轨道动力学模型[27]进行滤波,可以精确估计出地球卫星的位置信息。
1.2 星光折射导航量测量的获取
最原始的星光折射信息来自于星敏感器拍摄的折射星图,从中可以提取出折射星的像素坐标,通过坐标转换,可以得到折射星的矢量方向,进而得到星光折射角和折射视高度。
1.2.1 折射星像素坐标(折射星矢量)的获取
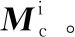

(2)
式中:f为星敏感器的焦距。
1.2.2 星光折射角的获取

(3)
1.2.3 折射视高度的获取
折射视高度是最早使用,也是目前研究最多的一种星光折射量测量,其获取方法比较成熟[6,30-31]。根据大气折射模型的经验公式[15,32],折射视高度hai可由式(4)通过星光折射角Ri计算得到:
hai=-21.740 898 77-6.441 326lnRi+
69.211 770 57Ri0.980 5i=1,2,…,nr
(4)
1.3 星敏感器安装方位的确定方法
星敏感器是获取星光折射量的重要敏感器,由于只有通过地球边缘大气层的星光才会发生折射,为了观测到折射星,星敏感器的光轴需要指向地球边缘,因此需要确定星敏感器的安装方位。星敏感器安装方位的定义如图3所示,θ为星敏感器光轴与地心矢量之间的夹角。星敏感器光轴应在锥线为地心矢量、锥角为θ的圆锥面上,并确保其始终指向地球边缘。φ为星敏感器光轴在地球卫星本体坐标系XOZ平面内的投影与本体坐标系的OZ轴(速度方向)的夹角,由于星敏光轴安装在轨道平面内导航精度较高,φ最好设为0°或180°[25]。
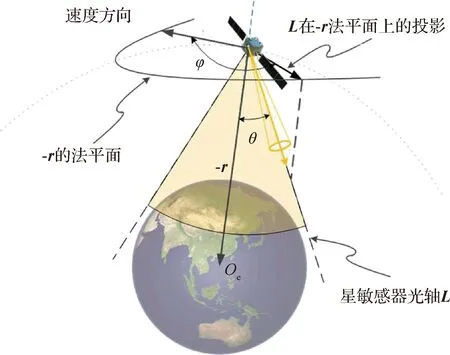
图3 星敏感器安装方案
星敏感器光轴与地心矢量间的夹角θ决定了星敏感器能否探测到折射星以及探测到的折射星的数量,应该保证星敏感器的视线不被地球边缘遮挡,并尽可能多的观测到折射星。夹角θ与卫星轨道高度h的范围及星敏感器视场FOV有关,夹角θ的计算方法如下:
1) 根据轨道高度h与地球遮挡确定星光角距范围
考虑到地球边缘的遮挡,只有星光角距α满足式 (5) 的恒星才能被星敏感器观测到:
(5)
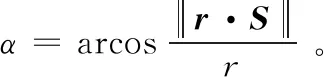
2) 由星敏感器视场确定折射星观测范围
星光折射的程度随折射视高度ha的增大而减弱,ha>50 km时,大气密度稀薄,折射效果弱,星敏感器难以捕获折射星;若ha太低,星光穿过存在各种剧烈的气象现象的对流层,同样不利于折射星的捕获;而折射高度在20~50 km的平流层内,温度变化缓慢,大气密度适中,无强烈对流,不含水蒸汽、气溶胶等随机性大的成分[30],大气折射角合适,可以取得较高的导航精度,是折射星较为理想的观测范围。
(6)
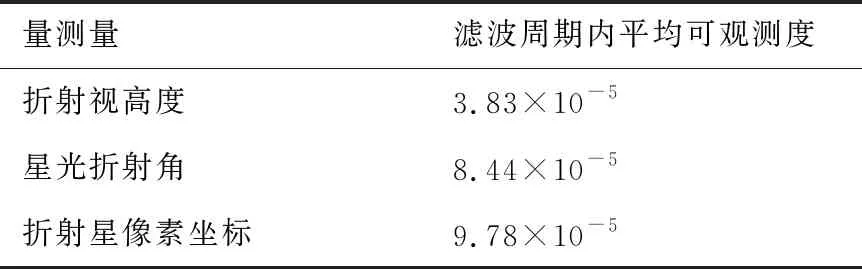
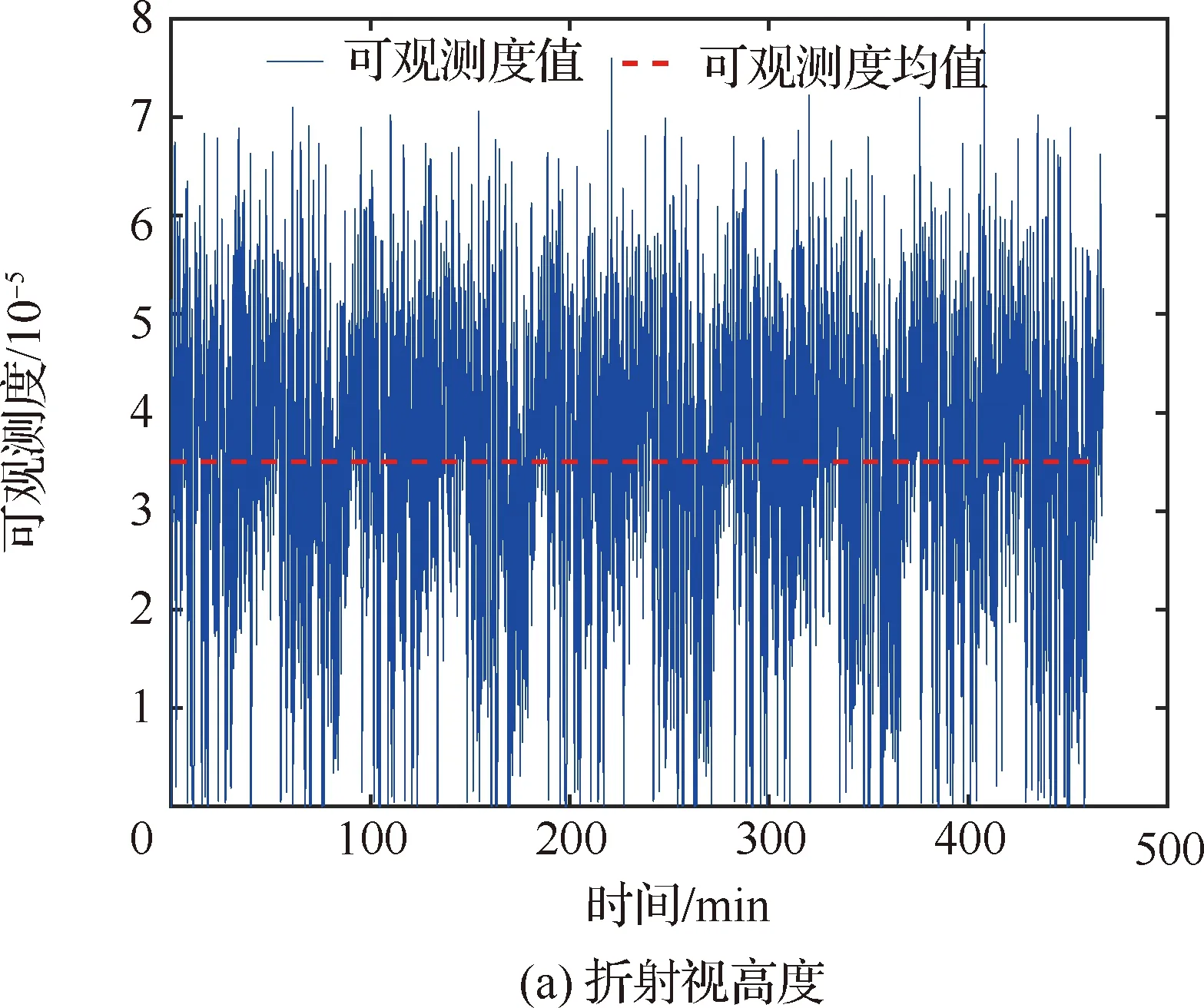
则根据式(6),可得ha在20~50 km范围内的恒星对应的折射角R范围为3″ 3) 夹角θ的最终确定 由于折射星光来自地平方向,为了尽可能多的观测到折射星,星敏感器视场可以适当被地球边缘遮挡。因此,结合星敏感器视场FOV和星光角距α,夹角θ应满足(α-FOV/2)≤θ≤(α+ FOV/2)。综上所述,对于轨道高度范围440~450 km的卫星,当星敏感器的视场为10°×10°时,夹角θ的范围为[65.2°, 74.4°],可设置为72°。该角度保证星敏感器能够同时观测折射星和非折射星,这也是折射星识别的基础[22]。 折射量测模型的建立过程与量测量的获取过程相反,因此本节先从最简单的折射视高度开始介绍。 由式(1)可得折射视高度的量测模型可表示为 Z1=ha=h1(r)+v1 (7) 式中:v1为折射视高度的误差。 构造基于星光折射角R的量测模型,实质上是建立星光折射角R与卫星导航参数之间的函数关系。联合式(4)和式(6),可得 -21.740 899-6.441 33lnR+ 69.211 77R0.980 5 (8) 由式(8)可知,星光折射角R与卫星位置矢量的模r和星光角距α三者有确定的函数关系,而星光角距α是位置矢量r与星光矢量S的夹角,因此星光折射角R与卫星位置矢量r存在函数关系。令Z2=R,其量测模型可表示为 h2(r,Z2+v2)=0 (9) 式中:v2为折射角误差,包括测量误差和式(8)的模型计算误差。 显然,星光折射角R的量测模型是一个隐函数,折射角R和卫星的位置矢量约束在一个隐函数中,无法获得显式的量测模型,解决这类含有隐式量测模型的估计问题,需要隐式量测模型滤波方法[23]。 折射星像素坐标(折射星矢量)的量测模型的建立主要包括3个重要步骤:星光折射角的计算,惯性坐标系下的折射星矢量计算,以及星敏感器坐标系下的折射星矢量和折射星像素坐标的计算[24]。 (10) (11) 式中:C为旋转矩阵,表达式为 (12) q1,q2,q3,q4为四元数,表达式分别为 (13) (14) (15) (16) 则基于折射星像素坐标或折射星矢量的量测模型可以简化为 (17) 式中:v3为折射星像素坐标量测噪声。 由于旋转矩阵C的四元数是由估计的折射角计算得到,因此当折射角估计存在误差时,矩阵C的计算必然存在误差,因此这一节对矩阵C的误差进行分析。 对式(12)左右两边同时微分有 (18) (19) 式(18)和式(19)表明矩阵C的误差不仅受折射角估计误差的影响,还受折射角R本身的影响。 当n确定时,可以确定C的误差与折射角R之间的关系,图4为转换矩阵C各个元素与R的大小和精度之间的关系,其中ΔCij(i=1,2,3;j=1,2,3)为C阵各个元素误差,可以看出随着折射角精度ΔR的减小,转换矩阵C的精度也相应的减小,并且随着折射角的改变,矩阵C的精度变化很小。 图4 折射角精度与转换矩阵C精度之间的关系 本节对上述折射视高度、星光折射角、折射星像素坐标(折射星矢量)3种量测量的星光折射导航系统性能进行了仿真比较。 3.1.1 轨道参数设置 卫星的轨道数据由STK软件[33]生成,轨道坐标系设置为J2000.0地心赤道惯性坐标系。轨道参数如表1所示,仿真时间为5个轨道周期的时间。卫星运行轨道如图5所示。 表1 仿真轨道参数 图5 卫星运行轨道图 3.1.2 星敏感器参数设置 星敏感器视场大小为10°×10°,所选星等为6.95m, 星敏感器精度1″对应的像素误差为0.711 pixels, 星敏感器光轴与地心矢量之间的夹角为72°。 3.1.3 滤波参数设置 1) 滤波周期为3 s。 2) 初始状态误差 ΔX0= [1 000 m,1 000 m,1 000 m,1 m/s,1 m/s,1 m/s]T 3) 初始系统噪声协方差阵 4) 系统噪声方差阵 5) 量测噪声方差阵 ① 折射星像素坐标的量测噪声方差阵Rk Rk=diag{(0.711)2, (0.711)2, …, (0.711)2} 其中,由于每个量测量对应的是二维坐标,Rk的维数是观测到的折射星数目的2倍。 ② 星光折射角的量测噪声方差阵R′k 假设第i颗折射星的折射角Ri及其星点像素坐标间关系可以表示为 Ri=hR(ui,vi) (20) 则星光折射角量测对应的量测噪声方差阵为 R′k=diag(HiRkHiT) (21) 式中: (22) ③ 折射视高度的量测噪声方差阵R′k 根据式(4)可知 hai=fha(R) (23) 则折射视高度对应的量测噪声方差阵为 R″k=diag(Hi′R′kH′iT) (24) 式中: (25) 3.2.1 仿真结果 图6为3种量测量的仿真结果图,图6(a)和图6(b)分别为位置估计误差曲线和速度估计误差曲线。表2为3种量测量的位置和速度估计误差曲线在滤波收敛后的平均值和最大值。由图6可以看出3种量测量曲线的估计误差在100 min后开始收敛,且3条曲线都随着卫星的轨道周期出现周期性的变化。3种量测量的位置估计误差曲线、速度估计误差曲线波动趋势基本一致。由图6和表2 可以看出,折射视高度的导航性能最差,星光折射角次之,折射星像素坐标的导航性能最好。相比较于折射视高度作为量测量,折射星像素坐标作为量测量时的导航位置精度和速度精度分别提高了38%和32%;相比较于星光折射角作为量测量,折射星像素坐标作为量测量时的导航位置精度和速度精度分别提高了36%和25%。这是因为折射星像素坐标作为量测量能够同时利用星光折射的大小和方向2个重要导航信息,而折射视高度和星光折射角作为量测量只利用星光折射大小一种折射信息,因此折射星像素坐标具有更好的导航精度。 图6 3种量测导航结果对比图 表2 3种量测量的导航结果 3.2.2 影响因素 为了进一步分析3种量测量的导航性能,该部分对不同星敏感器精度、不同轨道高度、不同安装夹角θ下的3种量测量的导航性能进行仿真对比。 表3为不同星敏感器精度下的3种量测量的导航结果。可以看出随着星敏感器精度的降低,3种 量测量的导航性能都有一定程度的降低,但是折射星像素坐标(折射星矢量)仍然保持最佳的导航性能。表4为不同轨道高度下的3种量测量的导航结果,可以看出随着轨道高度的增加,由于可观测到的折射星数量减少,量测信息相应地减少,从而导致了3种量测量的导航性能的降低,但是折射星像素坐标(折射星矢量)然保持最佳的导航性能。表5为不同安装夹角θ下的3种量测量导航结果,可以看出,在1.3节所求出的夹角范围内,该夹角的改变对3种量测量的导航性能影响相对较小,且本文所选择的72°夹角能够表现出较好的导航性能。 表3 不同星敏感器精度下的3种量测量的导航结果 表4 不同轨道高度下的3种量测量的导航结果 表5 不同安装夹角θ下的3种量测量导航结果 3.2.3 可观性分析 1) 可观测度的计算 由于状态估计的精度与系统的可观测度密切相关[34],为了进一步的分析3种量测量的导航性能,本小节对基于3种量测量的导航系统的可观测度进行分析。 可观测矩阵可构造为[35] (26) 式中:Φk,k-1为状态转移矩阵,表达式为 (27) Hk为等效量测矩阵,以折射视高度为量测量时,由于其量测模型为一般的非线性量测模型,因此可利用式(28)进行求解[1];以星光折射角和折射星像素坐标为量测量时,由于前者量测模型为隐式量测模型,后者量测模型建立过程复杂,因此采用式(29)进行求解[23]。 (28) Hk=(Pxy,k)T·(Pk|k-1-1)T (29) 式中:Pxy,k,Pk|k-1分别可由隐式无损卡尔曼滤波的状态估计误差协方差阵[23]和经典无损卡尔曼滤波方法状态估计误差协方差阵的计算方法获得。 可观测矩阵Mk(k=1,2,…)含有m维,其中m大于状态量Xk的维数。当且仅当可观测性矩阵Mk对所有的m均为满秩时,系统可完全观测。 本文以条件数的倒数作为系统可观性好坏的标准参数,可观测度的定义为[36] (30) 式中:σmax(M)和σmin(M)分别代表可观测矩阵M的最大和最小奇异值。 可观测度D(M)满足条件0≤D(M)≤1,当D(M)=0时,表明此时系统是不可观测的;当D(M)>0时,表明系统是可观测的,且可观测度越大,系统的估计精度也就越大。 2) 仿真结果 图7分别为以折射视高度、星光折射角、折射星像素坐标为量测量的星光折射导航系统的可观测度。表6为3种量测量整个滤波周期内的平均可观测度,可以看出以折射星像素坐标为量测量的导航系统具有较高的可观测度,导航精度较高。 表6 3种量测量的可观测度 图7 3种量测量的可观测度 1) 本文对星光折射导航中折射星像素坐标(折射星矢量)、星光折射角、折射视高度3种量测量的获取以及量测模型的建立进行了介绍,将基于3种量测量的星光折射导航方法应用于星光折射导航系统中进行仿真验证与分析。 2) 折射星像素坐标(折射星矢量)作为一种比折射视高度和星光折射角都更为直接的量测量,能够同时包含星光折射大小和折射方向反映这两个折射信息,具有更好的导航性能。仿真结果和可观测性分析都证明,以折射星像素坐标(折射星矢量)为量测量的星光折射导航系统在几种仿真条件下都具有最好的导航性能,基于星光折射角的导航系统的导航性能次之,基于折射视高度的导航系统性能最差且具有较大的实际应用限制。 3种量测量的导航性能都随着星敏感器精度减小而变差,因此在实际应用过程中,可以根据实际的指标要求选择合适精度的星敏感器;同样地,3种量测量的导航性能都随着卫星轨道高度的增加而变差。同时,本文也验证了,只要星敏感器光轴与地心矢量间的夹角在合理的范围内,夹角的选择不会对系统性能产生较大影响。在实际应用中,应综合考虑卫星轨道高度与星敏感器精度,选择满足需要的导航方法。 3)星图识别过程中“阈值”的设定,目前仍根据定位精度和星图精度通过经验和测试进行人工设定,该“阈值”能够自设定的方法是需要待进一步研究的问题。2 量测模型的建立
2.1 折射视高度的量测模型
2.2 星光折射角的量测模型
2.3 折射星像素坐标(折射星矢量)的量测模型



2.4 旋转矩阵C的误差分析


3 仿真比较
3.1 仿真条件

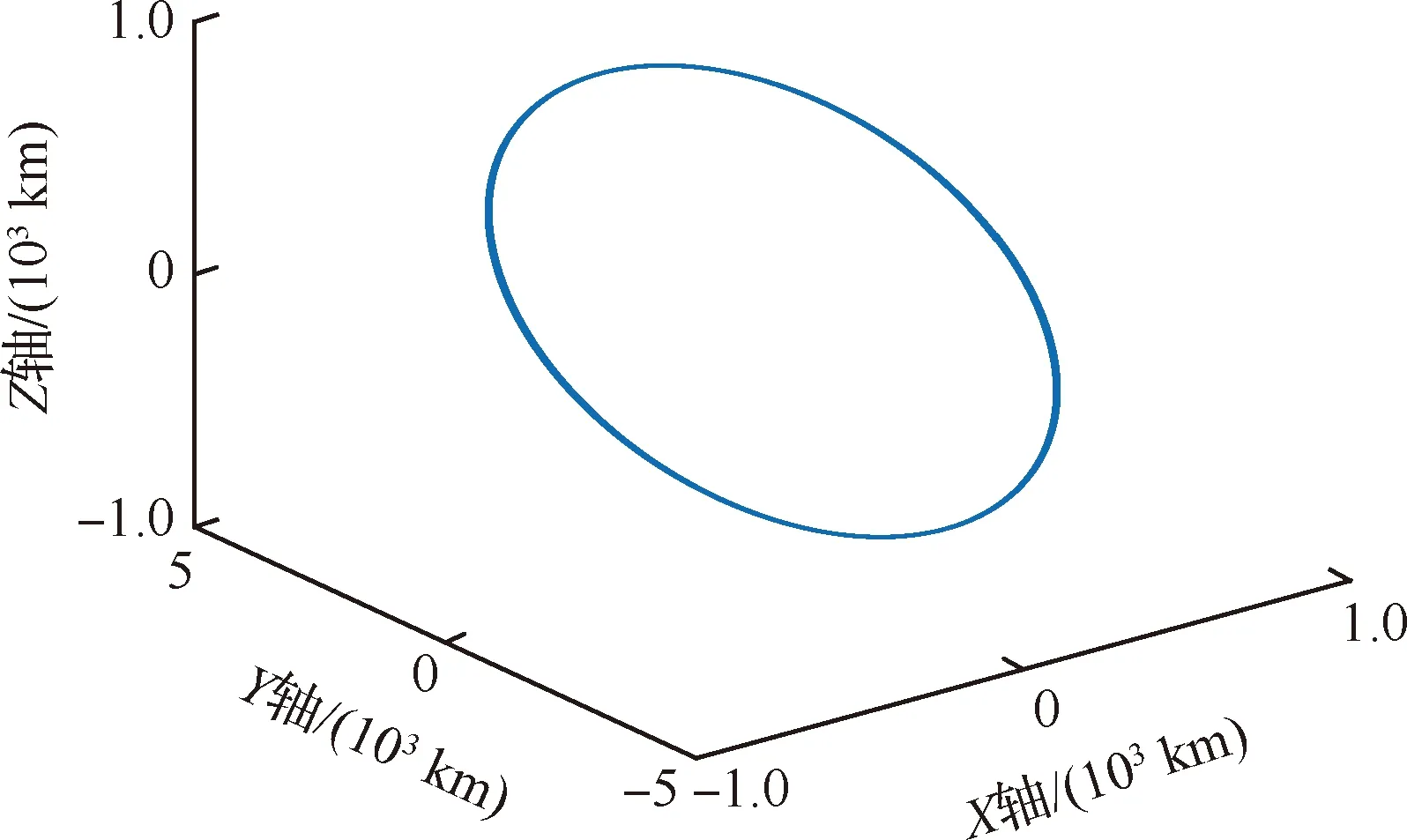
3.2 仿真结果及分析


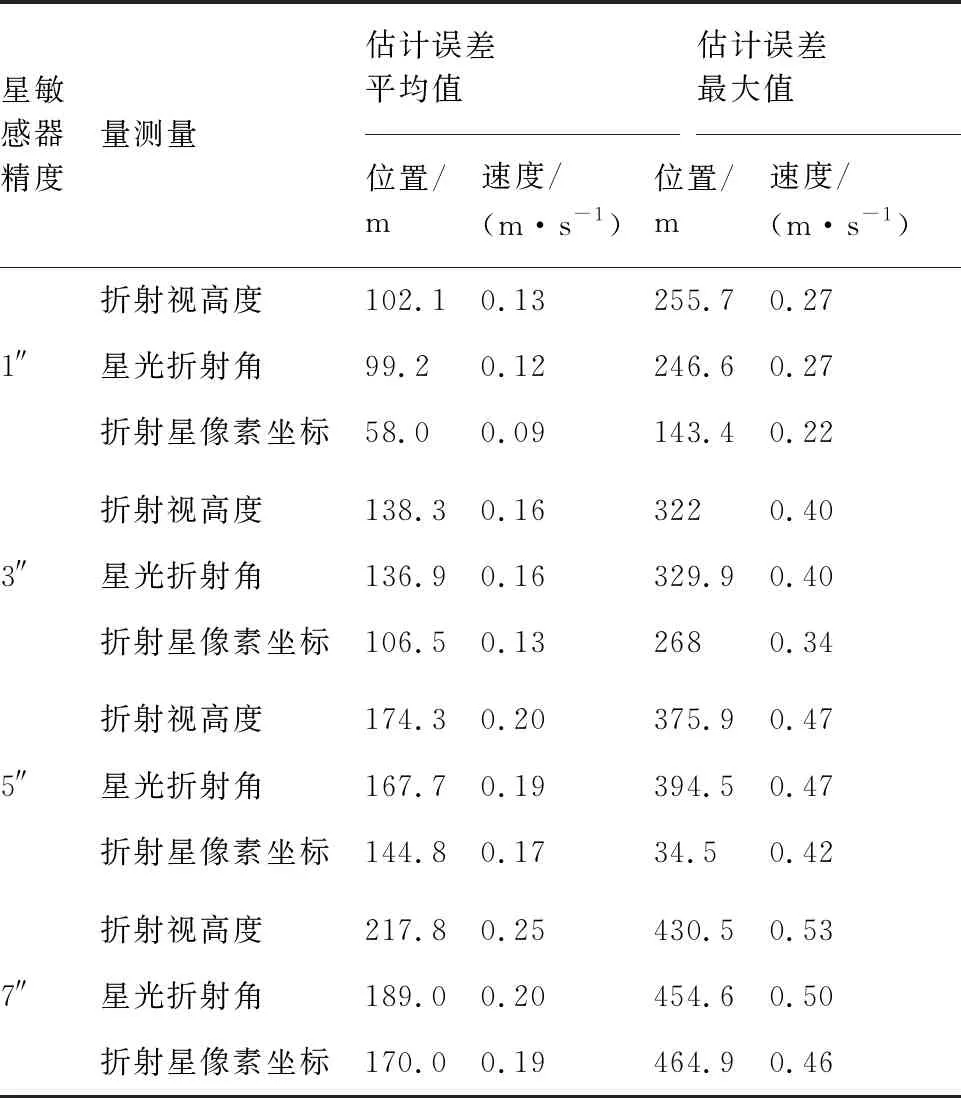
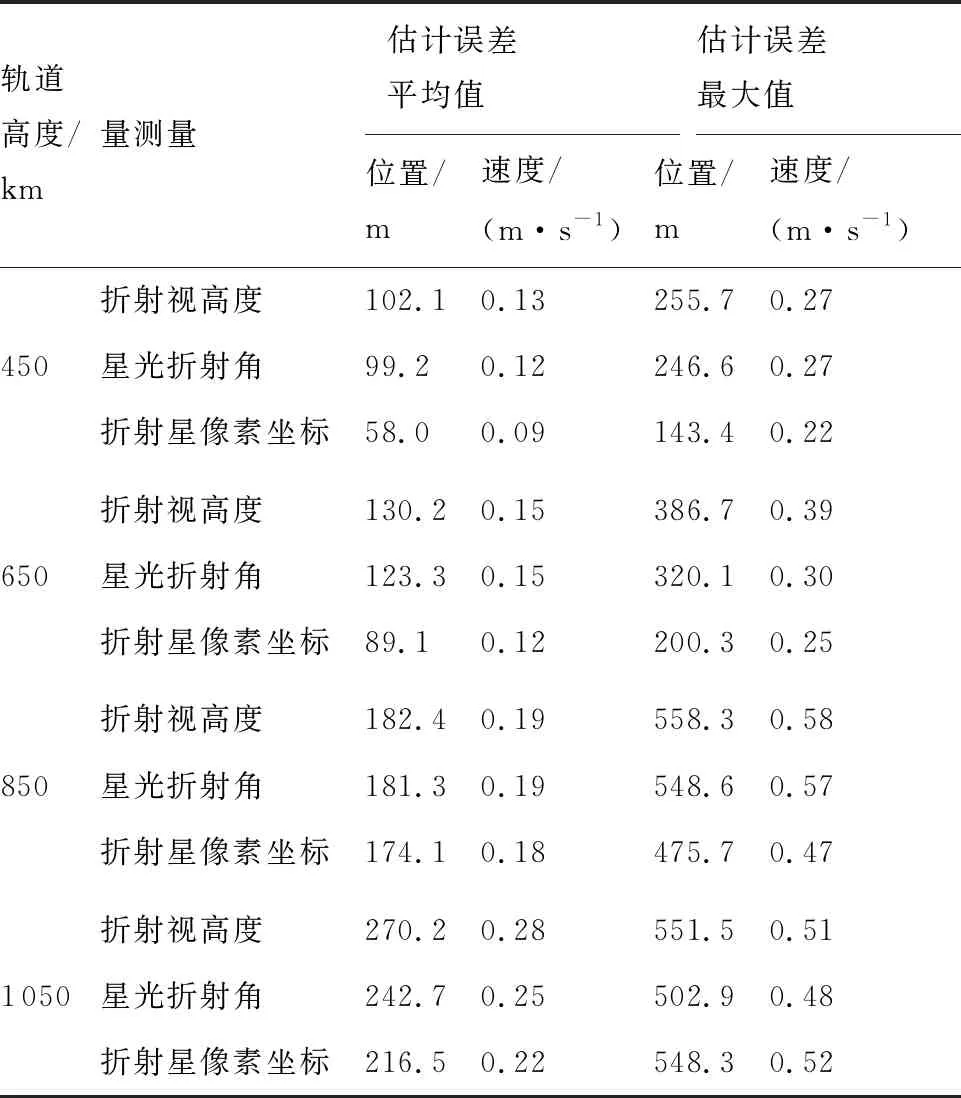
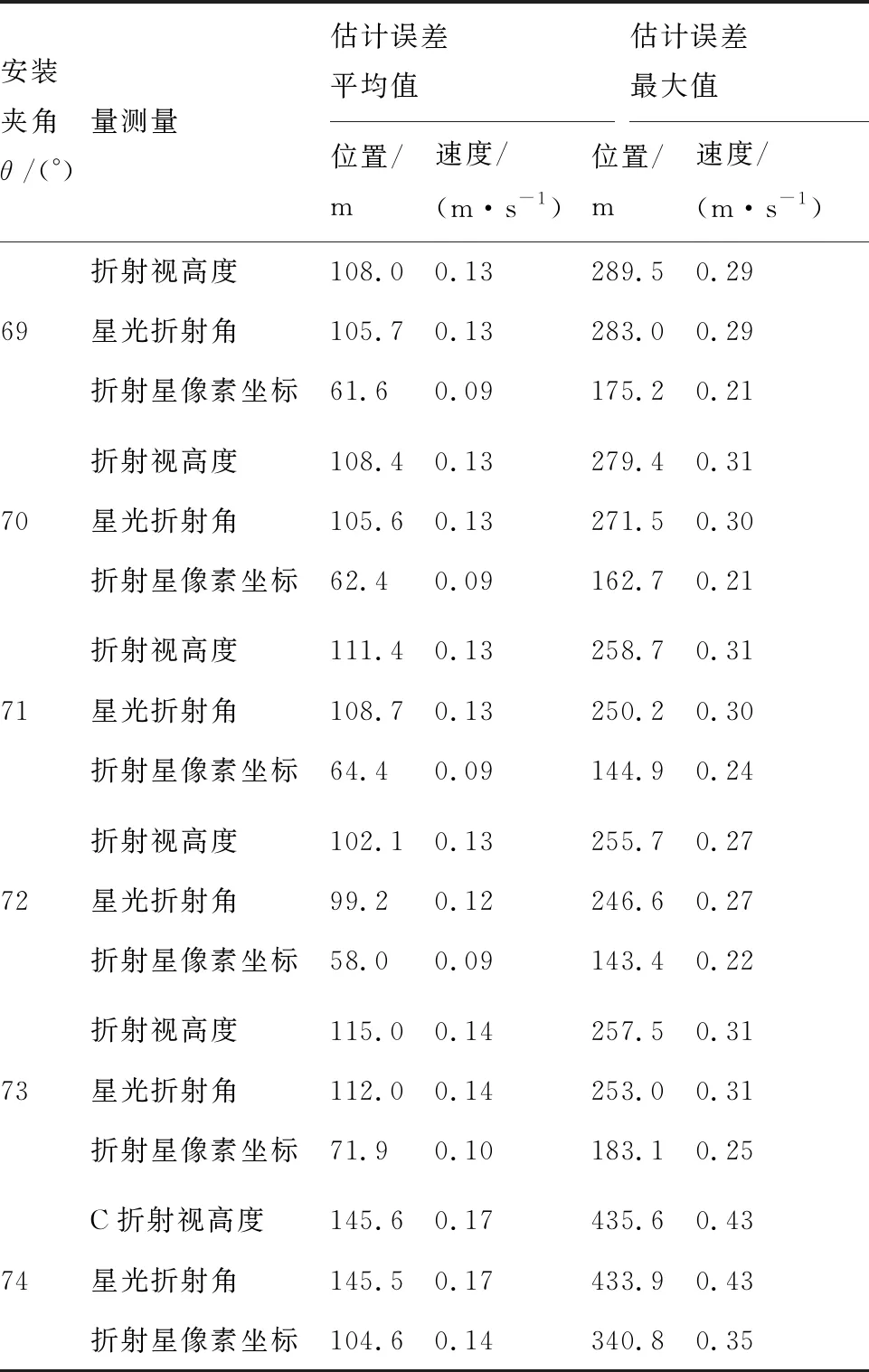
4 结 论

