有限元粘弹性人工边界的验证

廖志华 梁腾龙

(广西大学土木建筑工程学院 广西 南宁 530001)

一、绪论

利用有限单元法进行地震动力分析时，所截取有限元模型尺寸比实际场地尺寸要小得多，地震波在有限元计算区域传播时，波动很快就传播到计算区域边界而发生反射，影响计算结果。若要保证在计算时间内，波动传播不到计算区域边界上，需要截取较大计算区域进行计算，处理办法为采用远置边界。所谓远置边界就是将人工边界取与广义结构距离足够远，其人工边界采用固定处理，上述处理避开了反射波动对监测点或广义结构的二次作用，保证结果精确。当地震动力分析计算时间较长，计算区域介质波速较大时，采用远置边界需截取较大计算区域。有限元计算是将有限计算区域划分为有限个单元进行分析，在单元大小确定的情况下，若计算区域过大，就会增加计算自由度而大量地消耗计算机资源。

建立合理的人工边界来模拟有限计算区域截断前的状态，同时能够合理模拟波动在截断介质中传播是十分有必要的[1]。动力学一般采用人工边界来模拟土体辐射阻尼，使得波动在截取有限计算区域内顺利透过人工边界而不产生反射，边界应力、位移在介质截取边界处与原来相同，以达到还原地震场的情况，保证模拟的精度。

粘弹性边界由Deeks于1994年基于柱面波动理论的基础上推导，弥补粘性边界存在的问题，保证截取计算区域边界既能模拟波动穿过边界被吸收的情况，同时模拟地基弹性恢复力情况。其基本思路是在截取有限计算区域边界上，通过设置阻尼来吸收波动，通过弹簧来模拟地基弹性恢复力。粘弹性边界是目前国内应用于波动动力分析的主要边界之一，诸多学者对粘弹性人工边界进行研究和改进并运用到实际问题的研究中，验证其适用性并取得许多有意义的研究成果[2]。

二、有限元模型的建立

本文通过建立模型验证设置的粘弹性人工边界的精确度。分别对远置边界模型和粘弹性边界模型输入正弦波，在中心设置观测点，对比观测结果。其中参数如下表1所示。

表1 模型的物理参数Table 1 Physical Parameters of Model

远置边界模型中，左侧长度L1=400，中间长度L0=20，右侧长度L2=400，高度为H=20，宽为10。

粘弹性模型长L=820，高H=20,宽为10，刚度方程及阻尼方程分别为：

Kbt1=0.5*G4/R cbt1=P4*cs1

Kbn1=1*G4/R cbn1=P4*cp1

图1 远置边界模型示意图Figure 1 Model Schematic Diagram of Distant Boundary

图2 粘弹性边界模型示意图Fig.2 schematic diagram of viscoelastic boundary model

三、结果分析

分别对建立的远置边界模型及粘弹性边界模型输入幅值为0.45的正弦波，得到观测点的位移时程曲线如图3(b)～(c)所示。

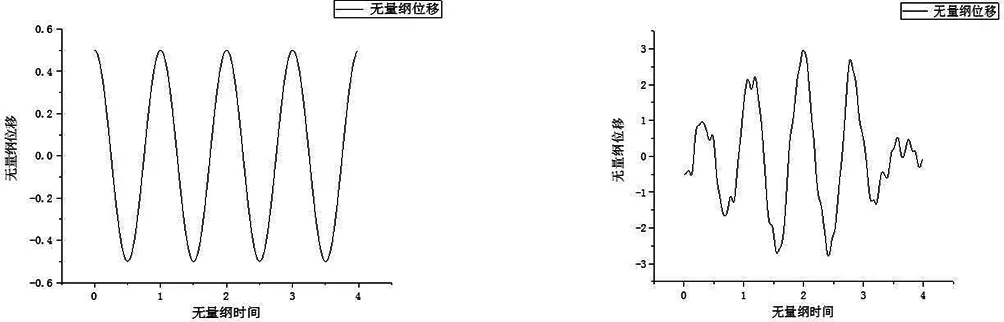
(a)输入的正弦波 (b)远置边界下的水平位移

(c)粘弹性边界下的水平位移 (d)两者对比 图3 两种边界下的检测位移曲线Fig.3 detection displacement curves under two boundaries

由图3可知，截断区域边界处采用粘弹性人工边界模拟计算结果与远置边界模拟计算结果在峰值上完全吻合，在非峰值处曲线也具有高吻合度，而采用固定边界的计算结果发生持续震荡。远置边界虽能得到逼近真实解的计算结果，但计算时间却是采用粘弹性人工边界的模型计算时间的50倍左右，这对于计算机资源产生极大消耗和浪费。表明采用弹簧-阻尼器组成的粘弹性人工边界能较好地模拟截断区域边界特性，在进行动分析时具有相当高的计算精度且有利于节省计算机资源。

四、结论

通过分别建立模型、输入地震波得到检测点的位移时程曲线，得出采用弹簧-阻尼器组成的粘弹性人工边界能较好地模拟截断区域边界特性，在进行动分析时具有相当高的计算精度且有利于节省计算机资源。