发电机无补偿相频特性测量理论与实践

（南京南瑞继保电气有限公司，南京 211102）

0 引言

自19 世纪60 年代中期，一些大型输电系统运行中频繁发生了有功功率低频振荡以及在大扰动事故后动态稳定恢复过程中的振荡失步故障。发电机Philips-Heffron 模型是电力系统有功低频振荡原理及其抑制器研究的基础，由之发展起来的PSS（电力系统稳定器），直至现在仍是提高电力系统正阻尼、抑制电力系统低频（0.1～2.5 Hz）振荡最经济有效的技术手段[1-4]。

在解释分析电磁力矩阻尼特性和有功功率低频振荡发生机理及抑制措施时，需要将Philips-Heffron 模型中功角处作开环处理，但发电机内部各量反应是物理过程，从外部无法实现开环，无法测量开环特性。研究表明，忽略无阻尼振荡影响时，闭环相频特性可以替代开环特性，工程实践中电压测量方便、准确[5-18]。但还需进一步研究，能否以电压闭环相频特性替代力矩或暂态电势闭环相频特性，以及2 种闭环特性产生差异的条件，对基于相频特性工作的阻尼力矩和PSS 参数整定会带来何种影响以及如何降低这种影响。

1 Philips-Heffron 模型与电磁力矩

发电机运行时各电气相量关系如图1（a）所示。以电气相量关系为基础，结合发电机机电运动方程，在运行点进行线性化数学处理，可获得转速增量Δω、功角增量Δδ、暂态电势增量、电磁力矩增量ΔMe2、电压增量ΔUt、励磁电压增量ΔEfd之间的关系，即发电机Philips-Heffron 模型，如图1（b）所示。图1（b）中顶部方框Ⅲ内为发电机机电运行方程，机械力矩ΔMm和ΔMe2经机电方程产生Δω 和Δδ 的框图；右下部方框Ⅰ内为励磁调节模块，Δδ 和产生ΔUt，与参考值ΔUref经励磁系统计算调节后，输出ΔEfd；左下部方框Ⅱ内为电磁力矩产生模块，Δδ 经电枢反应和ΔEfd导致，进而产生ΔMe2。

图1 发电机电气相量关系与Philips-Heffron 模型

图1 中：K1为固有同步转矩系数；K2为磁场磁通转矩系数；K3为阻抗比系数；K4为电枢反应系数；K5为功角差电压系数；K6为磁场磁通电压系数；为发电机暂态电势；为发电机时间常数；Ge（s）为发电机励磁调节传递函数；TJ为发电机机械时间常数；D 为发电机阻尼系数；δ 为发电机内电势与系统电压相角差；US为系统电压；I 为发机定子电流；Eq为发电机内电势；EQ0为发电机等效内电势；Xd，Xq，为发电机阻抗；Utd，Utq分别为发电机端电压横轴和纵轴分量；ψ为发电机内电势与定子电流相角差；Xe为外阻抗（含主变电抗和联接阻抗）；GPSS（s）为PSS 的传递函数，下同。

根据发电机参数及运行时各相量之间关系，图1（b）中各系数计算公式为：

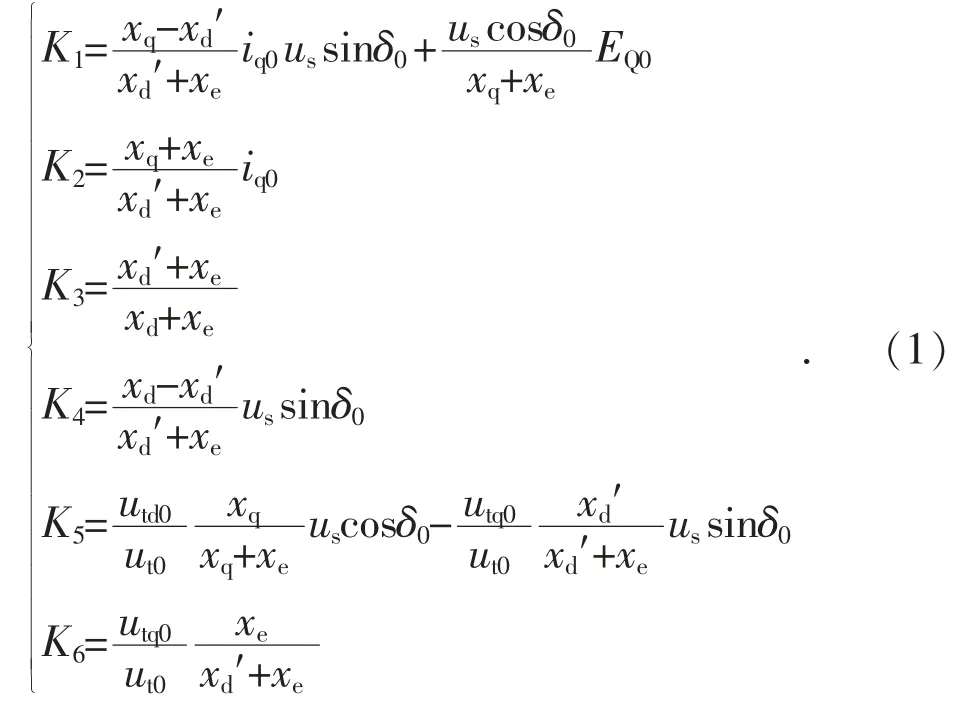
以上各系数，正常运行时除K5外均为正，K5在功角小时大于0，功角大时可能小于0。

发生有功低频振荡时，人工干预影响可以忽略，图1（b）中ΔMm和ΔUref为0，发电机电磁力矩产生有两个物理过程：一个是电枢反应（K4）（Ⅱ），另一个是励磁调节（K5，K6）（Ⅰ），见图2。

图2 发电机励磁及力矩框图

2 实测发电机无补偿相频特性方法

基于Philips-Heffron 模型的力矩阻尼分析可知，将Δδ 相关量（-ΔPe）与一个正系数的乘积引入励磁调节，其产生的附加力矩ΔMPSS的阻尼特性为正，正阻尼分量幅值大小由励磁调节模型参数及Philips-Heffron 模型决定，当ΔMPSS与Δω 方向相同时最大。这是PSS 模型参数整定试验的目标，希望PSS 产生的附加力矩ΔMPSS都是正阻尼力矩，即PSS 输出信号ΔUPSS在Δδ-Δω 平面上相位，加上ΔMe2与ΔUPSS之间的相位差，刚好与Δω 同向，如图3 所示。

图3 PSS 相频特性与附加力矩关系

由于K2＞0，ΔMe2与相位相同，ΔMe2与ΔUPSS之间的相频特性也就是与ΔUPSS之间的相频特性，称与ΔUPSS之间的开环相频特性为理论上励磁调节在线无补偿相频特性，Philips-Heffron 模型各量相互作用是各个物理过程，实践中不能人为分割，无法测量开环相频特性。研究表明，忽略发电机机电方程（s2TJ+sD+K1ω0）在无阻振荡频率区间造成的差异，闭环传递函数相频特性可以替代。理论上可以设计专门工具测量闭环，但较为困难，工程上电压测量准确、方便，故考虑以ΔUt电压测量替代测量，这需要分析ΔUt闭环传递函数与闭环传递函数的差异性。为便于理解和分析，将图2 中K4与K5部分等效分解，图2 转化为图4。

图4 两种闭环框图示意

图4 中下部虚线内为电枢反应函数，记为Gq（s）；上部虚线内为ΔUt形成函数，记为Gu（s）。

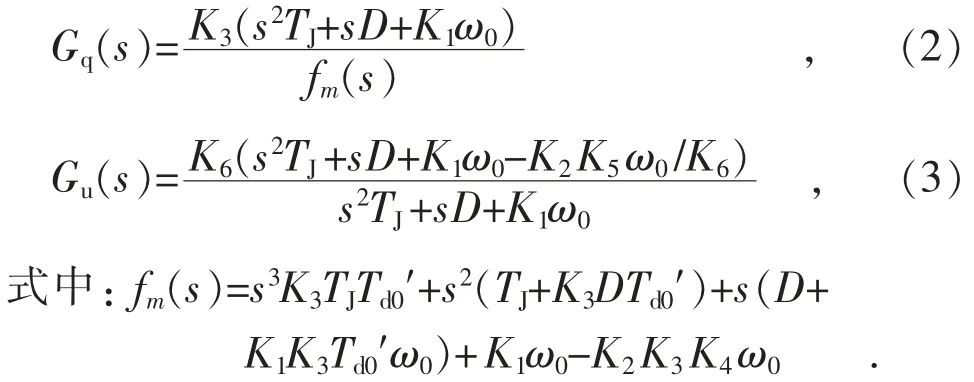
将图4 按传递函数方式转化为图5。

图5 基于Philips-Heffron 模型的传递函数框图

根据图5 可获得ΔUt和闭环传递函数分别为：

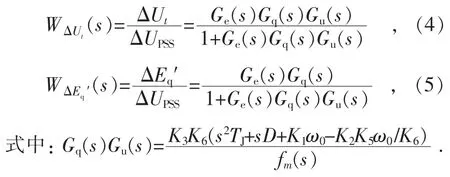
比较式（4）和式（5）可知，WΔUt（s）与WΔEq′（s）的分母相同，仅分子有差别。WΔUt（s）分子为：

比较式（6）与式（7），由于系数K6不影响相频特性，相频特性差别仅由于其分子的二次多项式零次项不同造成，二次多项式为发电机机电方程式。由式（1）可知，ω0=2×π×50≈314，零次项系数K1ω0、二次项系数TJ与一次项系数D 相差越大，其相位在无阻尼振荡频率附近有突变。图6为某工况下零次项不同时，机电方程相频特性示意图，除各自的无阻尼振荡频率附近外，低频段和高频段基本相同。

图6 机电方程典型相频特性

式（6）与式（7）分子除二次多项式零次项外，其余完全相同，也就是仅二次多项式的无阻尼振荡频率点不同，差别项为K2K5ω0/K6，与K2，K6和K5相关。由式（1）知，在发电机运行中，仅K5有过零的可能。

进一步分析式（4）的相频特性φΔUt与式（5）的相频特性φΔEq′差异性规律。当K5=0 时，差别项等于0，即φΔUt与φΔEq′同相位，这从发电机图1（b）的Philips-Heffron 模型也可以看出，当K5=0 时，ΔUt=×K6，故φΔUt与φΔEq′相同。若K5≠0 时，则φΔUt与φΔEq′不相同，K5＜0 时，无阻尼振荡频率变大；K5＞0，无阻振荡频率变小。

无阻尼振频率变化时，φΔUt与φΔEq′在其无阻尼振荡频率附近均会发生相频特性突变，在各自的无阻尼振荡频率附近，φΔUt与φΔEq′差别较大，在其余频段差别较小，K5绝对值越小，φΔUt与φΔEq′相位差也越小。

3 两种实测相频特性之间差异影响因子

以某电厂机组及励磁调节模型为例，计算两种测量发电机无补偿相频特性分别在K5＞0，K5=0，K5＜0 条件下有功出力的关系：

机组参数：Xd=2.0，Xq=2.0，=0.33，=8.5s，TJ=8.0s；

电网参数：Xe=0.1，US=1.05；

励磁模型参数：Ks=500，Tc=4.0s，Td=40.0s。

3.1 K5 变化趋势曲线

根据式（1）计算发电机有功功率不同条件下，K5随无功功率变化趋势，结果如图7 所示。

图7 K5 随无功功率变化曲线

由图7 可以看出：K5过零点在进相区域，随着有功功率的减小，进相加深；在无功功率为0时，随有功功率增加而减小。

3.2 K5＞0 时，发电机有功功率不同

K5＞0 时，不同有功功率下各系数取值如表1所示。

K5＞0 时，有功出力不同的3 种工况下的φΔUt与φΔEq′相频特性如图8 所示。

图8 K5＞0 时不同有功下3 种相频特性对比

由图8 可以看出：不同有功负荷下，开环特性基本一致，在低频段有稍许差异；φΔEq′在低频段受有功出力影响明显；φΔUt受有功出力影响较大，有功越小，其相位突变频率点越低；φΔUt和φΔEq′在高频段与低频段一致性较好。φΔUt和φΔEq′开环特性在无阻尼振荡频率点相差很大；在低频段，随着有功的增加，其差值有减小的趋势，即有功功率越大，越靠近开环特性；在高频段，基本相同，与有功出力无关。另外从无功出力看，随着有功的减少，K5一致时，无功越来越小，当P=0.4 时，已经是深度进相。

3.3 K5=0 时，发电机有功功率不同

K5=0 时，不同有功功率下各系数取值如表2所示。

K5=0 时，有功出力不同的3 种工况下的φΔUt与φΔEq′相频特性如图9 所示。

由图9 可以看出，不同有功出力下，φΔUt与φΔEq′基本相同，与前面理论分析一致。各个相频特性曲线在高频段没有差别，在低频段，有功出力小时，滞后相位变大，有明显差异，随着有功功率的增加，φΔUt与φΔEq′闭环相频特性与开环相频特性差值减小。另外，要达到K5=0，不同有功出力时发电机均需要进相运行，有功额定时，进相很小，当有功较小时，需要深度进相，已不利于发电机运行。要达到K5＜0，需要无功进相更深，不适合测量试验，这里不再讨论。

表1 K5＞0 时不同有功功率下各系数取值

表2 K5=0 时不同有功功率下各系数取值

表3 P=0.9 时不同无功功率下各系数取值

图9 K5＞0 时不同有功下3 种相频特性对比

3.4 P=0.9 时，无功功率不同

P=0.9 时，不同无功功率下各系数取值如表3 所示。

P=0.9 时，无功功率不同的5 种工况下的φΔUt与开环相频特性如图10 所示。

图10 P=0.9 时不同无功下相频特性对比

由图10 可以看出，无功功率在-0.1～0.3 的变化过程中，开环相频特性基本一致，φΔUt在低频段与高频段也基本一致，区别主要在无阻尼振荡频率及影响区域大小上，随着无功功率的增加，影响区域越来越大，以在-0.1～0.1 的区间内为宜。

4 结论

发电机无补偿相频特性决定PSS 作用的效率，是PSS 参数整定的基础，工程中测量无补偿相频特性有暂态电势和机端电压2 种方法。本文根据发电机Philips-Heffron 模型，从理论上分析2 种测量方法的差异性，并用实例计算各种影响因子的相关性，比较分析结果如下：

（1）2 种测量方法获得的无补偿相频特性，在高频段一致性较好，在低频段与有功出力相关，有功功率出力越大，闭环相频特性越接近开环相频特性，越准确。

（2）2 种测量方法差异性与K5系数相关性极强，当K5=0 时没有差异，K5数值越大，在无阻尼振荡频率范围内，差异越大。

（3）K5与发电机有功和无功出力均相关，要达到K5=0，有功出力不同，无功需求也不同，当有功额定时，无功在零附近，在实际工程中方便进行测试，而随着有功出力减小，进相深度越深，对试验安全越不利。

综上，实际工程中，建议在有功出力接近于额定、无功功率接近于0、功率因数接近于-1.0或1.0 时、K5接近于0 时测量电压闭环无补偿相频特性，此时无补偿相频特性相对更准确，以此结果整定PSS 相位补偿环节参数，有利于提高励磁调节正阻尼力矩。