莱州湾潮余流及粒子运移特征

姜悦,褚忠信,刘鑫仓,姜瑾斐,孙家高

(中国海洋大学海洋地球科学学院 青岛 266100)

0 引言

莱州湾位于山东半岛北侧,西起黄河口,东至龙口屺姆角,是渤海三大海湾之一[1],有黄河、淄脉河、小清河、弥河、潍河和胶莱河等河流汇入湾内[2]。

许多学者对该海域进行大量研究,研究成果集中在围填海工程[3-6]、水交换[7-9]、潮流波浪特征[10-11]和物质输运[12-16]等方面。在物质输运方面,海藻和塑料等重量较轻和易随海流运移的物质会在潮流作用下自由运移,其运移方向、运移路径和运移趋势等对海洋生态环境保护和沿岸地区生产生活具有指导意义。近年来针对莱州湾物质输运的研究逐渐增多,但对莱州湾粒子运移路径和运移规律的探讨较少。本研究运用二维数值模拟得到莱州湾潮流场和余流场,将重量较轻和易随海流运移的物质统一用自由运动的粒子代表,利用MIKE 21 HD模型计算不同初始位置的粒子在潮流作用下的运移轨迹,并分析莱州湾粒子运移的基本规律。

1 数据和方法

1.1 数据来源

本研究的岸线数据提取自2018年的Landsat 8卫星影像,空间分辨率为15 m,通过下载并配准卫片解译和提取岸线,并利用AutoCAD 进行调整[17]。采用海洋潮流发生一般高潮时海水所淹没的平均界线法提取岸线,研究表明平均高潮线的精度可满足当前的网格计算要求[18]。采用电子海图经水深插值取得计算水深和DHI-Cmap 水深数据。采集2个观测点(C5和C6)于2014年5月28日12时至5月29日12时的实测潮流数据[6],并与模拟数据进行验证(图1)。

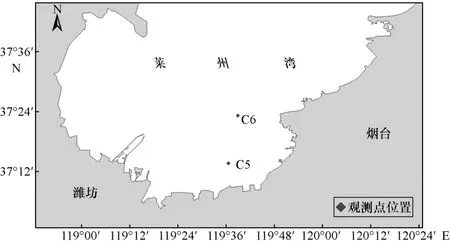
图1 观测点位置

1.2 数值模型

采用丹麦水力学研究所研发的平面二维数值模拟,对莱州湾的潮流场、余流场和物质输运进行分析[19]。MIKE 21 HD 遵循Navier-Stokes方程、Boussinesq假定和静水压力的假定[20],以此为基础建立方程[21]：

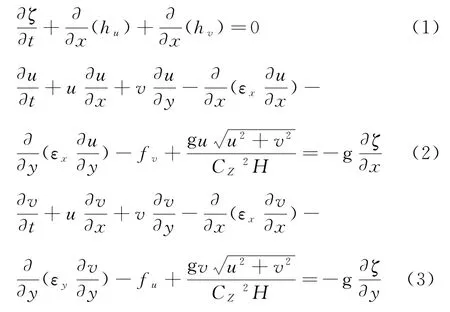
式中：ζ为水位;h为静水深;H为总水深,且H=h+ζ;u和v分别为x和y方向上的平均流速;g为重力加速度;f为科氏力系数;C Z为谢才系数;εx和εy分别为x和y方向上的水平涡动黏滞系数[22]。

1.3 计算区域和开边界

利用非等距网格技术对研究区域进行空间离散,并利用非等距三角形网格对重点研究区域进行加密[23],研究区域的计算网格分布如图2所示。

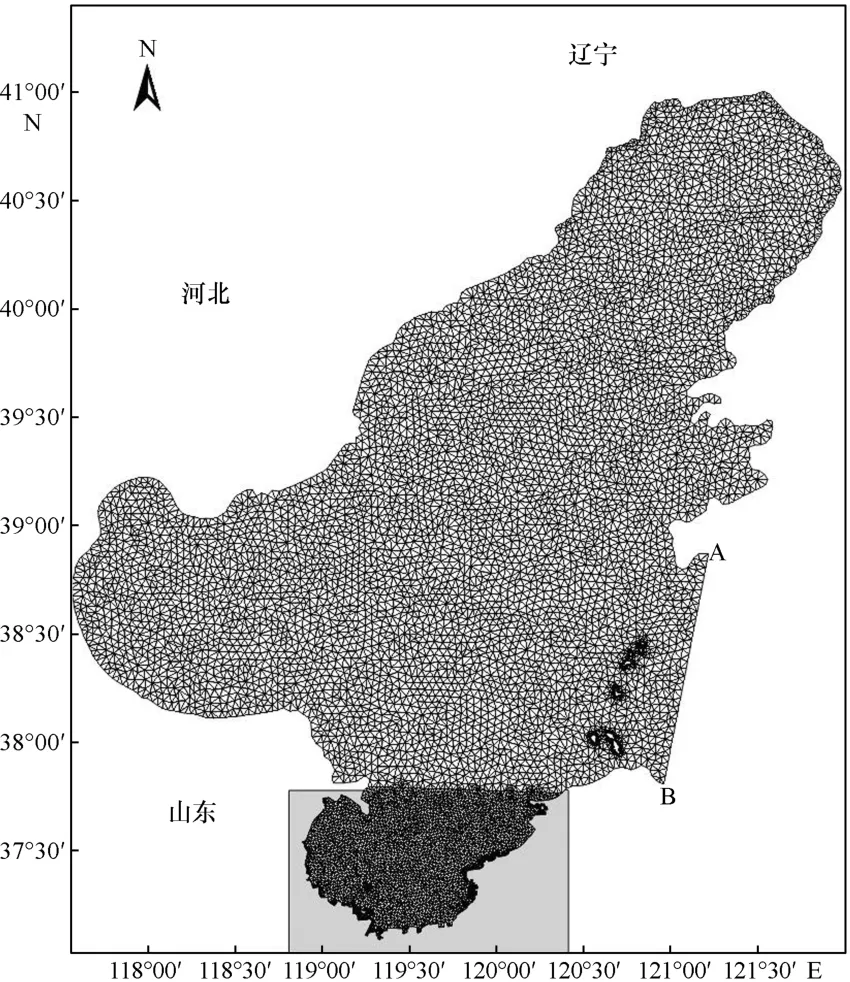
图2 模拟计算区域的网格分布

水动力模型的闭边界为渤海湾岸线,开边界为水位边界。开边界考虑4个主要分潮即M2、S2、O1和K1,经调和常数计算进行预报获得,由图2中的A、B二点连线组成,水位表达式[24]为：

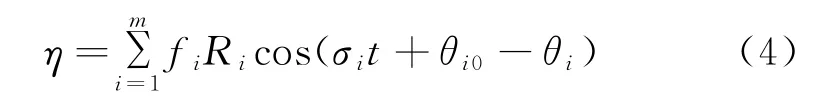
式中：f i为各分潮的交点因子;R i为各分潮的振幅;σi为第i个分潮;θi0为各分潮的初相位;θi为各分潮的滞后相位;m为分潮个数。

开边界的调和常数由MIKE 21 HD 全球模式中获得[25],并根据模型的具体情况进行调整。模型共有10 002个节点和18 522个三角网格,其中渤海的最小空间步长约为2 000 m,莱州湾的最小空间步长约为700 m。模型计算时间步长根据CFL 条件进行动态调整,以确保模型计算的稳定性,最小和最大计算时间步长分别为0.01 s和30 s。

1.4 欧拉余流和粒子运动

在研究动力理论时,通常采用欧拉速度计算余流。海洋中的欧拉余流可简单定义为欧拉平均速度,具体计算方法是构造x、o、y右手直角坐标系,并对流速沿x轴和y轴分解,分解后的欧拉余流的计算形式[26]为：

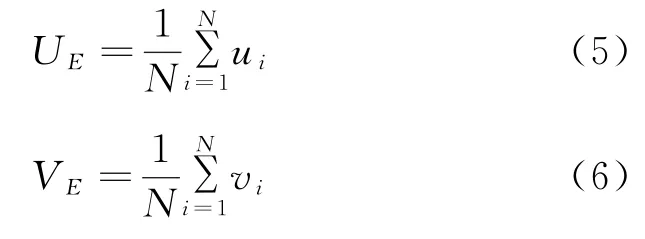
式中：U E和V E分别为x和y方向上的欧拉平均速度;N=n T/dT,其中n为所取计算周期的个数,T为潮周期,dT为数值模拟的时间步长;u i和v i为模型计算的每个时步在x和y方向上的速度。通过合成U E和V E得到欧拉余流场。

在进行粒子追踪时,在莱州湾内的一定位置释放自由粒子,并追踪粒子在1 440 h内的运移路径。考虑平流和水平扩散等因素,计算公式[27]为：

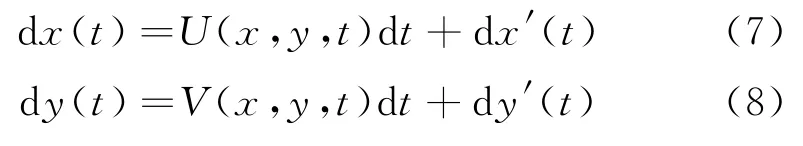
式中：dx'(t)和dy'(t)为水平湍流扩散引起的自由位移;U(x,y,t)和V(x,y,t)为x和y方向上的分速度;x(t)和y(t)为跟踪粒子的坐标[28]。

粒子的初始和结束位置如图3所示。

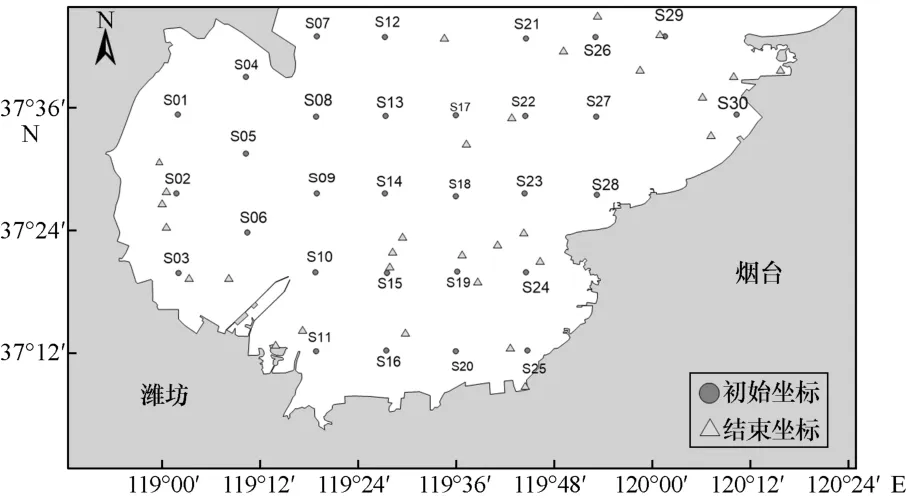
图3 粒子的初始和结束位置

1.5 模型验证

潮流流向和流速的验证结果如图4所示。

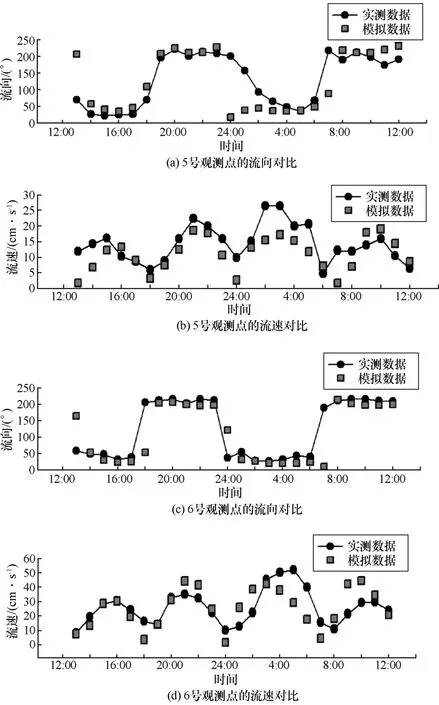
图4 流向和流速实测值与模拟值的对比

从流速和流向[29]的验证结果来看,2个观测点的模拟值与实测值基本吻合,相位偏差较小。总体来看,流速和流向的验证结果良好,表明模型配置合理,能较准确地反映莱州湾的水动力特征以及满足当前研究需求[30]。

2 结果和分析

2.1 涨急、落急流场

莱州湾附近海域涨急时和落急时的潮流场如图5所示。

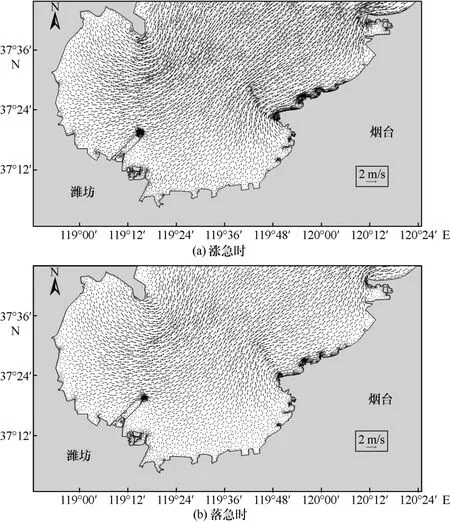
图5 莱州湾涨急、落急流场

莱州湾是半日潮为主的海湾,潮流运动形式以往复流为主,潮流方向与海湾的走向基本一致。①涨急时,潮流流向基本呈向岸方向,整体近SW向,在黄河口南侧海域呈NE向;渤海入湾区的流速最大,约为2.19 m/s,并向湾内逐渐减小。②落急时,潮流流向与涨急时相反,即基本呈离岸方向,整体近NE 向,在黄河口南侧海域呈SE 向,这与徐唯强[1]和刘建强等[5]的研究结果相似;流速的变化规律与涨急时相似,即由内向外逐渐增大,亦在湾口处获最大流速,约为2.66 m/s。

在潍坊港附近,涨急时的潮流流向为SW 向,落急时的潮流流向为NE 向,堤坝两侧的潮流方向顺堤坝流明显[31-32]。潍坊港改变附近海域的潮流流向,涨急、落急时的流速均出现不同程度的减小[33]。因此整体而言,堤坝的建造对莱州湾潮流造成的影响不容忽视,这与吕婷等[3]和田艳等[4]的研究结果一致。

2.2 欧拉余流场

根据莱州湾潮流场的情况以及式(5)和式(6),获得莱州湾欧拉余流场(图6)。

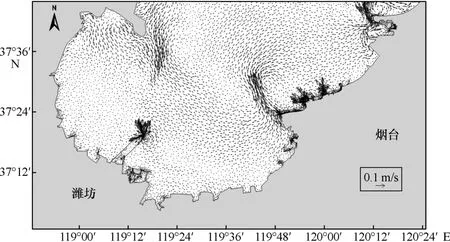
图6 莱州湾的欧拉余流场

欧拉余流表示流速垂线平均的潮平均项[34]。莱州湾的欧拉余流整体较小,平均值为1.95 cm/s。余环流在莱州湾的分布特征为：①黄河口南侧海域出现2个方向相反且流速较大的环流;②芙蓉岛和刁龙嘴附近海域即莱州湾东南部出现2 个较大环流,其中左侧为逆时针环流,右侧为顺时针环流,流速较其他区域稍大;③潍坊港附近出现1个流速较小且范围半径较小的顺时针环流。上述结论与迟万清等[7]的研究结果相似。

从分布规律来看,欧拉余流与潮流的相同之处在于均为湾口附近较大而湾内较小,不同之处在于欧拉余流在近岸区域明显大于中央区域。

2.3 粒子运移轨迹

在利用模型获得潮流场的基础上,本研究在莱州湾的不同位置释放自由运动的粒子,得到潮流作用下自由运动的粒子运移轨迹(图7)。

粒子运移轨迹可大致分为6 种类型：①由初始位置经短距离运移后抵达海岸或在附近停留,如S02、S03、S11、S16、S25 和S30;②由初始位置向SW 向 长 距 离 运 移,如S01、S04、S05、S06 和S10;③由初始位置向E 向长距离运移,如S12、S19、S20、S21、S26和S27;④由初始位置向SE 向长距离运移,如S07、S08、S09、S13、S14、S15、S18和S29;⑤由初始位置向NE 向长距离运移,如S17、S22和S28;⑥由初始位置向NW 向长距离运移,如S23和S24。

整体而言,分布均匀的粒子在潮流作用下出现不同程度和不同方向的聚集,但不同初始位置的自由粒子均呈现向岸运移的趋势。

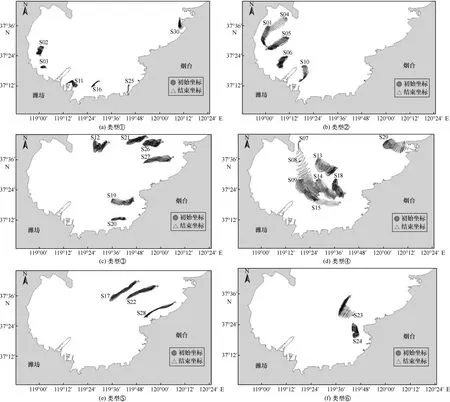
图7 粒子运移轨迹

3 结语

本研究采用MIKE 21 HD 模型得到莱州湾的潮流场和余流场,并在不同初始位置释放自由运动的粒子,获得在潮流作用下自由运动的粒子运移轨迹。以此为依据,分析莱州湾潮余流的时空分布特征以及具有相同特征粒子的运移特征,主要得到3项结论。

(1)涨急、落急时的潮流变化规律表明：莱州湾的潮流运动方向涨急时以湾外向湾内流动为主,落急时与涨急时相反;涨急、落急时的流速变化规律相似,即均在湾口处获得最大流速;潍坊港的建造改变附近海域的潮流流向,并不同程度地减小潮流流速。

(2)莱州湾的欧拉余流场表明：莱州湾的欧拉余流整体较小,平均值为1.95 cm/s;湾内出现4个半径和流速较大的环流,潍坊港附近出现1个半径和流速较小的环流。

(3)在潮流作用下,莱州湾分布均匀的粒子在自由运移时出现不同程度的聚集,且整体运移趋势是向岸聚集;具有相同性质粒子的运移距离出现较大差异,主要与其初始位置有关,即初始位置靠近海岸的粒子运移距离较短,而初始位置在湾内的粒子运移距离较长。