基于双向邻居修正的局部异常因子算法
杨晓晖,刘晓明
(河北大学网络空间安全与计算机学院,河北 保定 071002)
1 引言
离群值检测是数据挖掘领域的热门话题,其任务是识别与大多数对象明显不同的数据对象,这类数据与其他现有数据表现形式不一致,通常包含部分关键信息,且信息不易被发现,但是具有很高的研究和应用价值。离群挖掘是数据挖掘和数据分析的重要分支,已广泛应用于欺诈检测[1]、垃圾邮件检测[2]、交通异常[3]、网络流量异常检测[4]、入侵检测[5-6]和社交网络异常用户发现[7]等领域。大多数现有的解决方案通常从全局角度来识别离群值,这不适用于高维和海量数据集[8-9]。随着获取信息技术的发展和高维、海量数据的爆炸性增长,采用传统方法进行全局异常值检测将非常困难。
2 相关工作
离群值,即数据中的不合理值,可以由不同的机制产生。现有检测算法主要分为基于统计、基于深度、基于聚类、基于距离和基于密度的算法。
在基于统计的离群值检测算法中,偏离标准分布的对象被认为是离群值[10],该类方法需要数据集相关的先验知识,不适用于高维或分布未知的数据集。
基于深度的离群值检测算法[11-13]将数据分成不同层次,根据分层结果将外层或容易分层的对象判定为离群点,但该算法在高维数据集上的效率较低。
在基于聚类的离群值检测算法中,距其聚类中心较远的某些数据对象被视为离群值[14],算法必须建立聚类模型才能检测离群值,因此检测效率较低。
基于距离的离群值检测算法因简单高效而被广泛使用。在基于距离的异常检测算法中,通过计算数据集中一个对象与其他对象之间的距离来发现异常值,但由于未考虑局部密度的变化,因此只能检测全局异常值,无法检测局部异常值[15]。
在基于密度的离群值检测算法中,Breunig 等[16]定义了局部异常因子(LOF,local outlier factor)算法,通过将每个对象的密度估计值与其k个最近邻居进行比较来计算对象的离群程度。LOF 算法已经广泛使用,但是存在参数敏感问题。为此,Ha 等[17]于2014 年提出一种不稳定因子(INS,instability factor)算法,该算法通过控制参数灵活地用于局部和全局检测异常值。当参数改变时,INS 算法的准确率变化很小,但是当精度稳定时,INS 算法精度并不高。
Jin 等[18]改进了LOF 算法,并提出基于影响域的异常值(INFLO,influenced outlierness)检测算法,对邻居的使用比较直接,将正向邻居和反向邻居都视为同等作用,从而计算得出异常值。由于对邻居的使用较简单直接,未考虑到最近邻居的异常程度,因此精确度不高。
Zhu 等[19]定义自然邻居(natural neighbor)及其搜索算法(nan-searching)来利用反向邻居[20],还定义自然影响空间(natural influence space)和自然邻域图(NNG,natural neighbor graph)[21],并在后续工作中利用自然邻居来约减邻居、降低噪声影响[22]。Ning 等[23]通过搜索互邻图(MNG,mutual neighbor graph)的稳定状态来找到合适的k值,虽然避免了参数的选取问题,但在计算异常值时自然邻居对邻居的使用比较简单,且准确率和效率较低。
因LOF 为无监督算法,Auskalnis 等[24]提出了用于网络入侵检测的LOF 算法模型来检测未知手段的攻击。Na 等[25]提出了数据流异常检测(DiLOF,distributed local outlier factor)算法,减少了存储开销和时间开销,但是仍存在参数选取困难的问题。Yao 等[26]提出了一种增量式局部离群值检测模型,用于数据流中的异常检测,虽然该模型使用了反向邻居,但只是将反向邻居作为邻居扩充,策略简单,检测性能略低。Yang 等[27]提出了一种邻居熵局部离群值因子(NELOF,neighbor entropy local outlier factor))检测模型,首先使用改进的自组织特征图(SOFM,self-organizing feature map)算法对数据集进行聚类,然后进行离群点检测,精度略有提高,但因聚类算法的加入,效率较低。Gao 等[28]提出了一种基于多维数据集的离群值检测算法,通过将高维数据切片并检测,降低了存储和时间开销,但数据切片会损失原有数据的高维特征,降低检测性能。Zhao 等[29]提出了一种半监督集成算法(ExGBOD,extreme gradient boosting outlier detection),使用集成学习的思想结合监督学习和无监督学习的优势,但弱化了无监督算法的泛化能力。
上述算法由于无法准确把握对象与邻域之间的关系,导致在复杂数据集上计算准确率较低。如图1(a)所示,假设其k值为3,此时对象p的3 个相邻对象具有比p更高的局部密度,即对象p将具有较高的局部异常值。但是在复杂数据集上,常规局部异常因子算法准确率并不高。如图1(b)所示,对象p是密集簇C1附近的稀疏簇C2的一部分,与对象q和r1相比,p应当具有较小的离群值。若使用常规局部异常因子算法,p可能被错误地认为与对象q具有相同大小的异常值。因此,现有的离群值度量方法不适用于数据集包含具有不同密度多个聚类分布的情况。由于对象最近邻居的错误选择,导致邻域密度分布的错误估计,从而计算出一个不准确的异常值。
为了更好地估计邻域的密度分布和计算局部异常值,使用最近邻居和反向最近邻居是必要的。如图1(c)所示,情况与图1(b)相同,但对象p具有2 个反向最近邻居:s和t。这没有将其与反向最近邻居的对象q区分开来,并且对象r1仅具有作为其反向最近邻居的异常r2对象。因此加入反向最近邻居能够较好地解决不同密度邻域间对象的异常值计算问题。
现有算法对参数具有高度依赖性,参数改变对异常值检测结果影响较大。另外由于没有充分利用反向最近邻居的属性,导致计算准确率不高。针对这一问题,本文提出了一种快速异常值检测算法,既充分利用双向邻居,也避免了参数选取问题。

图1 不同密度簇间对象的异常计算问题
3 结合双向邻居的异常值计算算法
针对局部异常因子算法及其他改进算法的不足,本文提出一种自动确定良好参数的修正局部异常因子算法模型。受page-rank 算法启发,CFLOF 算法将反向邻居经过特殊处理后再参与到对象的异常值计算中,若所有反向邻居无差别地参与异常值计算,将存在误判问题,导致计算准确率较低。例如,在微博用户异常检测中,把“僵尸粉”算作真正的粉丝是一种错误处理,因此本文提出修正因子的概念来改善这种问题,并通过第4 节的实验验证了这种处理是有效的。
算法主要由2 个部分组成:基于双向邻居的影响域(IS,influence space)和用于解决不同密度簇之间对象异常计算问题的修正因子(CF,correction factor),如式(1)所示。
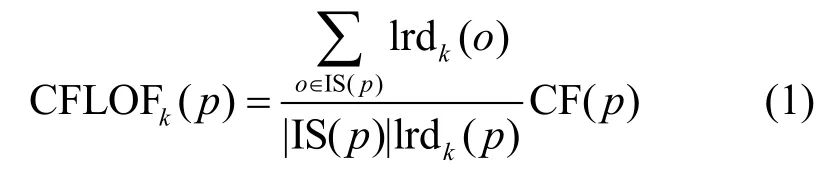
其中,IS(p)为对象p的影响域,o为IS(p)中的对象,lrd(p)为对象p的局部可达密度,CF(p)为对象p的修正因子,则对象p的修正局部异常值(CFLOF,correction factor local outlier factor)被定义为对象p局部可达密度与其影响域IS(p)中对象局部可达密度均值的比值乘以对象p的修正因子CF(p)。
3.1 基于双向邻居的影响域
在算法计算的过程中,搜索对象的双向邻居需要占用大量的时间,因此需要采用高效的算法来寻找邻居节点。目前,主要使用K-D 树或R 树来索引对象,从而加快邻居的搜索速度[19]。因此在邻居搜索过程中,使用空间树结构来索引数据集中的所有对象,并通过特定的修剪技术降低邻居节点查询的成本。由于查询对象的最近邻时是通过遍历数据集的子集来计算临时第k距离(k-dist(p)),且k-dist(p)的上限值已知,当p与R 树中叶子节点最小边界矩形(MBR,minimal bounding rectangle)之间的最小距离(记为MinDist(p,MBR))大于当前的k-dist(p)上限值,则节点中的任何对象都不会是p的k最近邻之一。此优化方法可以修剪与K 近邻(KNN,K-nearest neighbor)搜索无关的整个子树。随着KNN 的搜索,每个对象的反向最近邻居(RNN,reverse nearest neighbor)可以在R 树中动态维护在建立KNN 和RNN 索引后,可以计算局部异常值并对其进行排序。算法1 是通过在R 树中构建KNN 和RNN 索引来挖掘异常值排名较高的n个对象。
。
算法1双向邻居搜索算法
输入k,D,R 树的根
输出双向邻居的堆空间 heap


双向邻居搜索算法首先初始化数据集堆空间和k-dist,依次摘取R 树中每一个MBR,比较MinDist(p,MBR)与k-dist 的大小。算法仅在那些MinDist(p,MBR)小于当前k-dist(p)的MBR 中搜索对象p的k最近邻居;当MinDist(p,MBR)大于当前k-dist(p)时,则这些MBR 被修剪,不需要搜索。每当找到最近邻时,它们就被存储为p的最近邻居,同时存储p作为反向最近邻居。最终CFLOF 基于影响域空间(KNN 和RNN)计算。
为推导双向邻居搜索算法的有效性,假设输入数据集为Xn{p1,p2,p3,…,pn},初始时从p1开始搜索k近邻和反向邻居,初始k-dist 设置为无穷,此时没有k近邻。通过R 树搜索其k近邻时,首先寻找R树中的MBR,R 树是B 树在高维空间的扩展,其每个MBR 中包含多个pk∈Xn,每个MBR 在R 树中索引了其上下界,例如在二维空间中使用4 个值标明其界限,组成一个矩形(rectangle,此为最小边界矩形MBR 的由来),因此可以通过计算p1与R 树中的MBR 的4 个角的距离,并取最小值记为MinDist(p1,MBR),若此最小值大于当前k-dist,则其下属节点不参与计算,从而减少计算量,提高时间效率。
本文使用基于反向邻居的修剪算法用于修剪计算过程中不需要计算的对象,且解决k值选取困难的问题,可以确定一个较优的k值。该算法具体介绍如下。
算法2基于反向邻居的修剪算法
输入D,R 树的根
输出输出CFLOF 值


通过迭代搜索数据集相对稳定的状态,当反向邻居为0 的对象在连续3 次迭代后没有变化时,且在循环数次后未产生变化时达到稳定状态,表明在此数据集中距离相近的对象均搜索到反向邻居,而可达密度低的对象无法搜索到反向邻居,最近邻空间达到一个稳定的状态,此时修剪反向邻居为空的对象即Rnb=0 的对象,最后通过上述迭代的结果计算CFLOF 值。
k值确定算法通过搜索反向邻居的稳定状态来实现k值选取。使用反向邻居的思想是通过反向邻居加强邻居密度准确率,因为只使用k近邻的情况下容易对数据点的密度出现错误的估计。现假设数据集为Xn,其中含有2 个密度不同的簇C1和C2,以及离群点q,如图2 所示。当k值为1、2、3、4时,离群点q没有反向邻居,此时k值的选取不会对q的计算产生影响,本文选取k=2 和k=4 作为参考;当k=5 时,离群点q新增了反向邻居,如果k值继续增加,q点的反向邻居则持续增多,此时会降低离群点检测的性能。因此k值选取算法可以确定一个良好的k值,此时k值选取的大小刚好使C1簇中的节点均存在反向邻居,而离群点q依旧没有反向邻居,因此k值选取算法能确定一个良好的k值用于异常值的计算,且在确定k值的同时可以修剪没有反向邻居的数据项,因为没有反向邻居,所以该数据项不与任何数据项为同类,这符合离群点的定义。
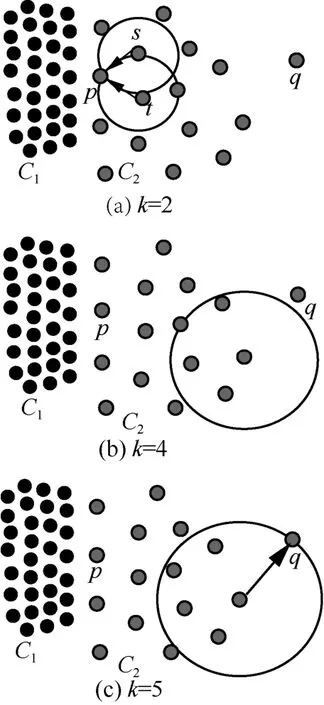
图2 数据集Xn
算法主要通过以下2 个方面提高效率。首先,对于任何对象p,除非所有其他对象都已完成最近邻搜索,否则无法确定RNN 空间,若使用普通的搜索方法会消耗大量时间,采用算法1 可以提高搜索效率。其次,通过分析LOF 的特征,对于数据集中的任意对象p,如果存在 RNN(p)=∅,则LOF(p)>>1。因此可以删除这些集群对象,既降低计算开销,又节省存储空间。
对于p∈D,如果对于任意一个对象p存在RNN(p)=∅,则LOF(p)>>1可以直接标为异常对象。因为RNN(p)=∅,即没有任何一个对象跟p“亲近”,所以对象p远离其他数据集中的对象,即对象p是局部异常值较高的点。
为了解决k值选取困难问题,通过算法2 搜索数据集的稳定状态,并选取稳定状态下数据集中最大的RNN 的个数即最大反向邻居的值作为k值。因为最大的反向邻居的值反映了聚类簇的模的大小,这样选取的好处是可以保证不会因为选取值的数目过小而造成准确率的损失,同时由于有反向邻居修正因子的存在,不会因为值略大造成错误的计算。通过对反向邻居的特性研究,本文定义影响域为

p的影响域定义为当k值取稳定状态下的
3.2 基于反向邻居的修正因子
max(Rnb)时其双向邻居的集合。影响域反映了与对象p相关的数据对象的范围。
修正因子算法借鉴了PR 算法,可以消除部分类似于“僵尸粉数据”对计算的影响,加上反向邻居修正可以提高不同密度邻域间对象的异常因子计算的准确度。原始PR 算法是根据对象的出入度来迭代计算影响值,因此将对象正向和反向近邻类比出入度来计算出一个节点的影响因子。最后将计算结果作为一个加权值放入原本的公式中,定义为修正因子,用于提高局部异常因子算法的计算准确度。
修正因子计算式为
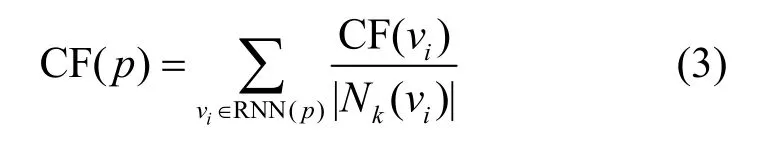
其中,CF(p)是对象p的修正因子值;CF(vi)是对象vi的修正因子值,对象vi是对象p反向最近邻居中的某个对象,即vi∈RNN(p);N k(vi)是对象vi指向其他对象的数目,即vi的正向最近邻居的个数。修正因子是通过对象的反向最近邻居传递的属性,给出一个此对象的可信任程度,充分利用反向邻居的作用,更好地计算局部密度值,提高了在密度不均的数据集上异常值计算的准确率,从而重新定义带修正因子的局部异常值。
CFL OF 计算式为

4 实验结果及评估
4.1 实验数据及流程
为了验证CFLOF 算法的高效率和高准确性,分别在合成数据集和真实数据集上进行实验,数据集类别如表1 所示。用于直观显示结果的二维合成数据集共有5 种,包含不同聚类的模式、不同程度的聚类密度和不同聚类簇的大小,如表1的序号1~5所示。基于5 个合成的二维数据集的实验主要用来直观地展示在二维合成数据集下算法的处理结果。为了更好地评估算法性能,在4.3 节选取了2 个合成的高斯数据集进行准确率和时间效率的实验,数据集如表1 的序号6~7 所示。同时选取6 个公开数据集进行实验,用于对比CFLOF 算法在真实数据集上的检测性能,数据集参数如表2 所示。在实验中使用2 种检测指标,即准确率和时间效率来评估所提算法的性能。

表1 二维合成数据集

表2 公开数据集
本文算法通过Python 语言来实现,合成数据集通过NumPy 库设置不同的均值和标准差来生成,实验操作系统为Ubuntu,内存为16 GB,CPU为i7-6700。
Letter 和Pendigit 数据集来自UCL 的数据库。Smtp 数据集来自KDD99 数据集的子集,其中服务属性为smtp;Http 数据集同样来自KDD99数据集的子集,服务属性为http。Credit 是信用卡欺诈检测的公开数据集。Mnist 数据集是手写数字数据库的子集。各数据集大小以及维度如表2所示。
4.2 参数调优
为了验证CFLOF 算法的有效性,使用5 个数据集进行对比实验,利用人工设置参数和不同的步长来进行实验。通过不同的实验发现,当k值变化在10 以内时,准确率变化较小,因此将k值变化的步长设置为大于或等于10。将不同k值情况下所得准确率数据绘制成图,并将算法确定出的k值进行标记,实验结果如图3 所示。

图3 不同k 值选取下的准确率对比
通过对5 个数据集的实验发现,自动参数k值的选择算法选择出的参数k是最优参数。在数据集1中,算法得到的k值为20,此时的准确率最高;在数据集2 中,算法选择的k值虽然没有达到最高的准确率,但是k值小于50,算法的时间效率较好。在数据集3 中,算法确定的k值达到了最高的准确率。数据集4 和数据集5 实验结果同样在使用算法确定的k值达到了最高的准确率。通过5 个数据集的实验对比发现,算法2 选取的参数k的值在准确率上都有不错的表现。实验结果表明,参数选择算法可以解决局部异常因子算法参数选取困难的问题。
4.3 合成数据集实验结果
为了直观地显示CFLOF 算法的准确性,本节首先在5 个二维合成数据集上进行实验,并对实验结果进行总结。这5 个二维合成数据集特点如表1 所示,包含不同聚类的模式、不同程度的聚类密度和不同聚类簇的大小,以便在复杂的测试环境中评估CFLOF 方法。将CFLOF 算法的性能与现有的2 种算法(LOF 算法和INS 算法)进行了比较。在每个算法中,具有最高局部异常值的对象在以下实验结果中被标记成星号形状。图4~图8 显示了3 种算法的离群检测结果。参数k的值是通过算法2 获取,而不是人工设置的。
图4 显示了数据集1 上3 种算法的实验结果,该数据集由3 个簇组成。数据集1 是较简单的情况,存在3 个标准高斯分布的簇。此数据集由1 500 个对象组成,其中4%(60 个对象)是异常值。由图4 中实线方框的位置可以看出,CFLOF 算法的准确度优于INS 算法,这是因为CFLOF 算法通过使用反向邻居增强了算法的检测能力,可以检测出一些INS 算法和LOF 算法漏检的对象。LOF 算法和CFLOF 算法的结果是相似的,并且在数据集1 的局部异常值检测上优于INS 算法。INS 算法的错误率明显高于LOF 算法,这是因为INS 算法错误地将簇中的值检测为异常值。

图4 数据集1 上3 种算法的实验结果(k=17)
数据集2 由1 000 个对象、4 个正式簇和85个异常值组成,如图5 所示。从图5 所示的结果可以看出,CFLOF 算法的全局异常检测效果与INS 算法类似,都比LOF 算法好。但是,在局部异常值检测中,LOF 算法和CFLOF 算法的效果优于INS 算法(一些局部异常值在实验结果中被实线框标记出)。INS 算法对反向邻居的利用较简单,而通过修正因子利用的反向邻居可以很好地在全局和局部上正确地检测出异常值,即当参数k的值被赋予17 时,CFLOF 算法的准确率在3 种算法中最高。

图5 数据集2 上3 种算法的实验结果(k=17)
图6 所示的数据集3 涉及局部密度问题。此数据集中共包含1 641 个对象,其中45 个对象是异常值。INS 算法的结果是3 种算法中最差的。INS 算法由于没有有效地利用反向邻居,导致错误地将位于实线方框中的正常点检测为异常对象,且无法正确检测出位于实线方框中的真实异常值。而LOF算法则错误地将下方密度均匀的簇检测为异常点,相比之下通过修正因子利用反向邻居改进后的CFLOF 算法在处理复杂数据集时,将反向邻居的影响考虑在内,提高了检测的准确定,检测效果好于其他2 种算法。

图6 数据集3 上3 种算法的实验结果(k=13)
图7 中所示的数据集4 涉及低密度数据问题。此数据集中共包含880 个对象,其中72 个对象是异常值。从图7 结果中可以看出,经过修正因子改进的CFLOF 算法在较稀疏的数据集上也可以很好地检测出异常值,不会出现错检的情况。这同时也验证了当参数k使用算法2 确定时CFLOF 算法的有效性。
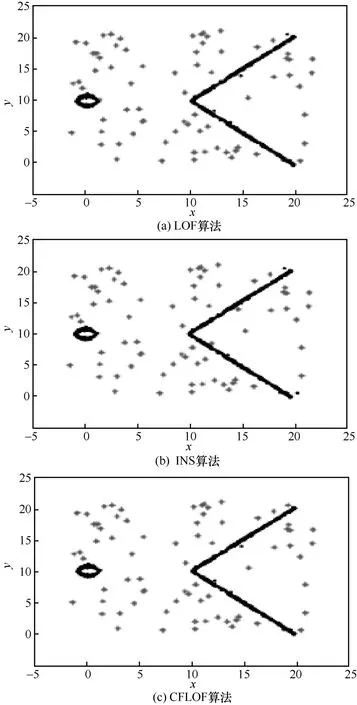
图7 数据集4 上3 种算法的实验结果(k=28)
如图8 所示,数据集5 具有低密度数据和不同流形的簇,由1 400 个对象组成,其中100 个对象是异常值。INS 算法的结果是最糟糕的。INS算法错误地检测位于实线方框中的点,这些点属于具有流形的簇,INS 算法再次错误地将正常簇中的点识别为异常值。而CFLOF 算法在使用反向邻居及修正因子以后,可以增强同簇对象间的影响,同时减少噪声的影响,对流形数据簇分布具有较好的识别效果,最佳低保留了数据流形分布规律。
上述实验结果直观显示了CFLOF 算法的优越性,CFLOF 算法在5 个数据集下的准确率均优于其他2 种算法,这表明修正因子的引入提高了算法在二维合成数据上的准确率。
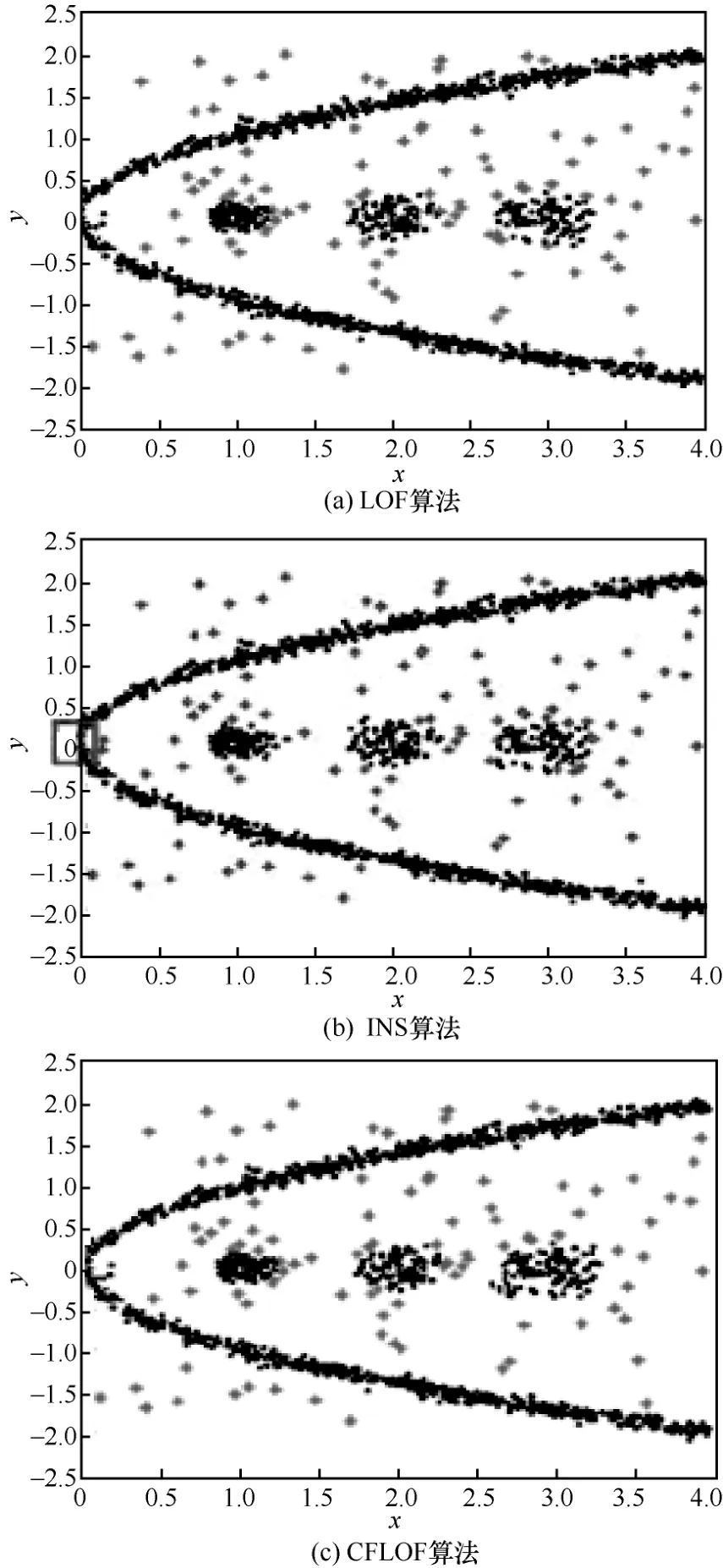
图8 数据集5 上3 种算法的实验结果(k=31)
4.4 算法模型时间效率对比
通过表1 中的高斯分布数据集1 和高斯分布数据集2 来测试算法的时间效率,如图9 所示。实验结果的起始部分随着使用数据集大小的增加,算法在构造R 树的时间开销较高。距离计算与邻居搜索的时间开销较低,随着数据集的增加,距离计算与邻居搜索的时间开销逐渐增大,而R 树的使用与后期的修剪过程减少了距离计算与邻居搜索带来的开销。当数据集规模持续上升时,可以看到,CFLOF 算法在数据集规模超过1.5×104时开始拉开差距,并且在后面数据集增大时差距逐渐变大。

图9 3 种算法的计算时间随数据集规模的变化对比
通过在符合高斯分布合成数据集上进行的实验发现,因所提剪枝算法的使用,可以有效地提高时间效率,相较于其他算法,CFLOF 算法在时间的效率上均有不同程度的优势。
4.5 公开数据集上检测性能实验结果对比
为了进一步验证CFLOF 算法的有效性,将CFLOF 算法应用于2 个真实世界的数据集。从UCI机器学习库中选择2 个具备不同属性的数据集:Pendigit 和Letter,用于算法的准确率和时间效率的测试。同时生成2 个符合高斯分布的数据集,维度均为2 维,数据生成的协方差矩阵和均值不同,大小可变,生成的数据将用于测试算法的时间效率。
在2 个真实的数据集上对3 种算法的准确率进行了对比实验,根据实验结果绘制了算法的准确率随k值的变化情况,如图10 所示,其中垂直虚线所对应数据点是CFLOF 的实验数据,因为其k值是通过算法2 自动确定的,所以仅标注k=20 和k=27 时对应的算法准确率,可以明显地发现,CFLOF 算法的准确率高于其他2 种算法,这验证了CFLOF 算法避免了参数选择的问题。通过实验结果还可以发现,参数选择算法不仅适用于CFLOF 算法,同时在其他改进局部异常因子算法中也可以得到较高的准确率。
为了更好地对算法的检测性能进行比较,验证模型在实际应用领域的检测效果,分别在4 个高维数据集上进行了实验,对于前3 个数据集(Http、Smtp 和Credit),使用高斯随机投影将维数减小为8。对于Mnist 数据集,由于原始数据是高维的,因此减小的子空间维数为15。将随机投影过程重复10次,然后比较不同算法之间ROC 曲线下与坐标轴围成的面积(AUC,area under curve)的平均值。

图9 3 种算法在2 个真实数据集下的准确率随参数k 的变化
同时将CFLOF 算法与目前主流的支持向量机(SVM,support vector machines)和iForest 进行比较,在Http 数据集和Smtp 数据集中,CFLOF 算法的性能与SVM 的最佳结果相似。在Credit 数据集和Mnist 数据集中,CFLOF 算法的平均AUC 比其他2 种算法更高。同时相比于其他2 种算法模型,CFLOF 算法模型更简单,时间开销小。

表3 3 种算法在公开数据集实验的AUC 均值
通过在真实数据集上进行的实验发现,相较于其他算法,CFLOF 算法在检测性能上有不同程度的优势,尤其是当进行多个聚类簇不同密度之间的对象计算时,CFLOF 算法的准确率比较高,这表明双向邻居搜索算法和修正因子提高了算法效率和准确率。同时通过KDD99 网络数据集和金融领域的真实数据上的实验结果发现,CFLOF 算法模型可以很好地解决现有的异常检测问题,同时CFLOF 算法模型相较于其他算法模型也有较好的表现。
5 结束语
针对目前离群点检测算法存在参数选取困难、精度低等问题,提出了基于反向邻居修正的局部异常因子算法来检测异常值和评估对象离群程度。与现有的基于距离和基于密度的算法不同,CFLOF算法不受模型参数k值变化影响,参数k值由所提双向邻居搜索算法确定。同时本文还提出修正因子的概念,该概念使CFLOF 算法在处理复杂数据集中对象时,可以更准确地计算异常值。在二维合成数据集和真实数据集下的实验结果表明,CFLOF算法相较于其他算法在时间效率和准确率方面有一定优势,这体现了CFLOF 算法的有效性。但是当维度过高时,CFLOF 算法有维度灾难问题出现,会导致基于距离的算法失效问题,如何寻找一个有效的并且对数据原始特征损失较小的降维算法,是未来的研究目标。

