某市政边坡失稳模式分析及加固设计

肖登峰

(福建省建筑设计研究院有限公司 福建福州 350001)

0 引言

随着我国城镇化的推进，城镇建设逐渐向郊区辐射，市政道路建设成了市政工程的重要内容之一，但市政道路建设引发沿线边坡滑塌事件时有发生[1]，边坡稳定性成了市政道路修建中不可忽视的问题。因此，在实际工程中需要对边坡采取经济有效的加固防护。

边坡设计需要建立在对边坡坡体结构和失稳模式分析的基础上[2]，失稳模式分析通常采用极限平衡法和有限元法。极限平衡法建立在多种假定条件下，对边坡的失稳模式分析与真实边坡存在较多差异。基于应力应变关系的有限元分析法则更为灵活方便，在分析复杂边坡的失稳模式上更有优势[3]。本文以某市政边坡作为研究对象，选取两个典型剖面分析其失稳模式，基于该边坡失稳模式选取加固防护措施，并结合有限元和极限平衡法评估该边坡加固后的稳定情况。

1 工程概况

该边坡为土质挖方边坡，长度约225m，高度7m，坡度20°～40°，走向北东，倾向南东。边坡坡脚距道路5m～6m，坡脚为道路及隧道工程；坡顶为林地，周边无建构造物。该边坡属于永久性边坡，边坡安全等级为二级，边坡主体结构设计使用年限为50年。根据相关规范，该边坡在一般工况的稳定安全系数需达到1.30，在地震工况时应达到1.10，如表1所示。

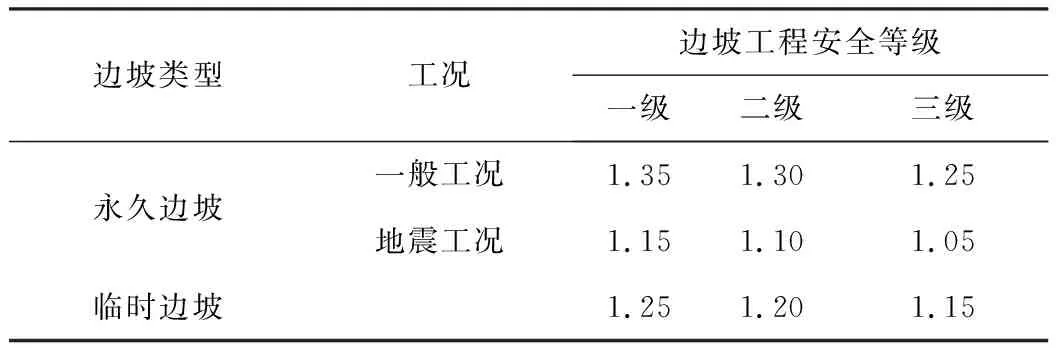
表1 边坡稳定安全系数Fs

2 工程地质条件

2.1 地层岩性

该边坡由残积土和风化基岩组成，从上到下分为5个地层，分别是素填土、矽线云母片岩残积粘性土、全风化矽线云母片岩、砂土状强风化矽线云母片岩和碎块状强风化矽线云母片岩。根据前期钻探资料，该边坡划分为15个剖面，如图1所示，部分剖面的钻孔资料未揭示碎块状强风化层。

2.2 岩土工程物理力学参数

根据现场取样和土工试验获取的数据，结合地区经验，确定该边坡岩土体的物理力学参数，如表2所示。

表2 岩土体物理力学参数表

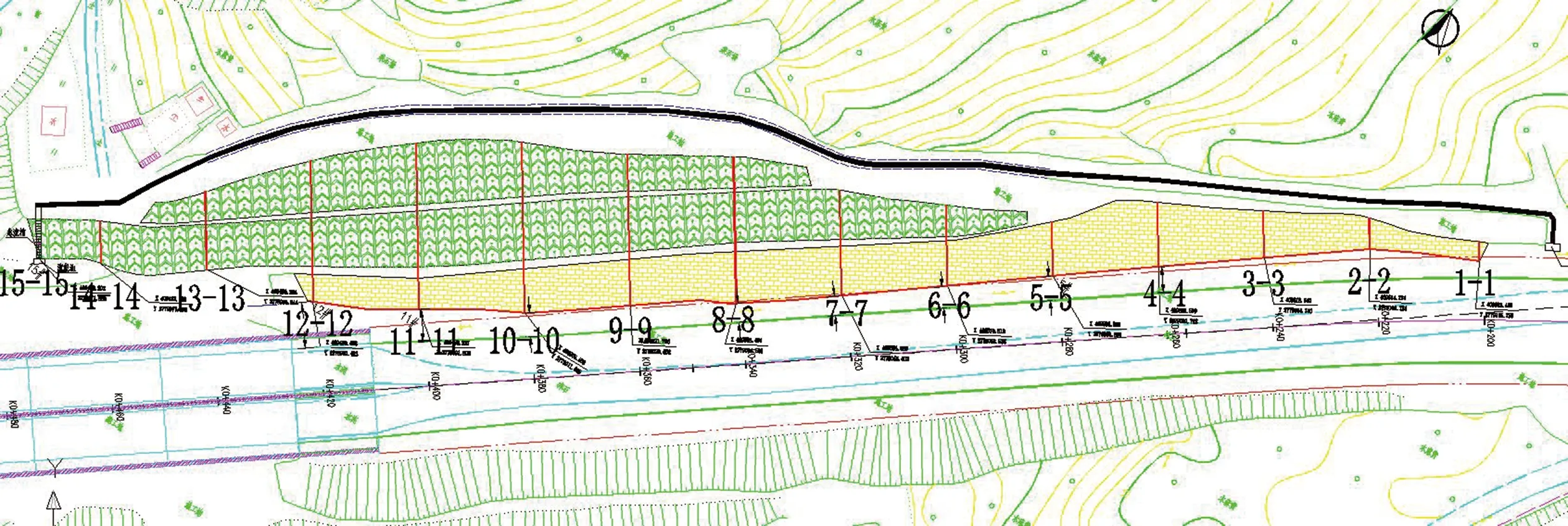
图1 某市政边坡概况

3 基于有限元的边坡失稳模式分析

探究边坡失稳模式是边坡加固设计的重要一步，其目的在于：针对边坡失稳模式，采取经济有效的加固措施达到稳固边坡的效果。边坡失稳模式的分析方法以极限平衡法和有限元法为主。极限平衡法通过预先假定滑动面计算最小安全系数，滑动面形状和依附界面与地层岩性、坡面形状和坡度等多种因素有关，因此基于极限平衡法分析边坡失稳模式有失偏颇。有限元法则是通过岩土体应力应变关系分析边坡滑动面，更接近实际边坡的失稳模式。故本文以二维有限元法分析该市政边坡失稳模式。

二维有限元即通过选取安全系数最小的典型剖面进行稳定性分析。初期的稳定性计算结果显示，以8-8剖面和10-10剖面最为不稳定。

3.1 建立数值模型

基于前期勘察钻孔揭示的坡体结构，建立有限元数值模型，选取Mohr-Coulomb本构模型，采用三角形网格将8-8剖面计算模型划分为4233个单元，10-10剖面的计算单元分为4172单元。两个数值模型如图2～图3所示。

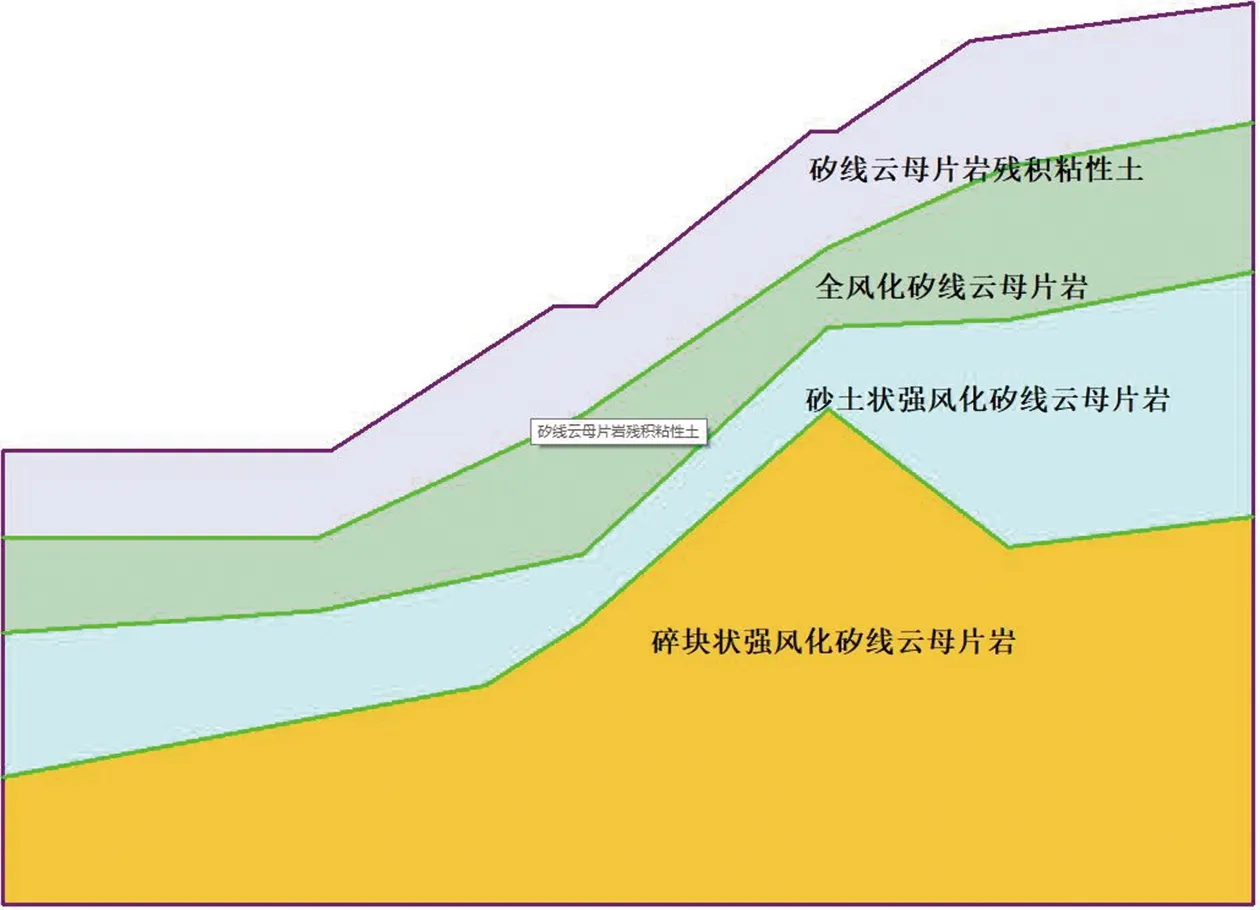
图2 8-8剖面数值分析模型

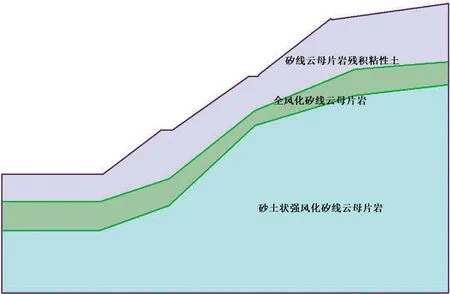
图3 10-10剖面数值分析模型

3.2 边坡失稳模式分析

图4 8-8剖面总位移变形图

该边坡类型为土质边坡，边坡所在区域降雨充沛，地下水主要赋存于坡体底部的碎块状强风化矽线云母片岩和中风化矽线云母片岩中，全风化矽线云母片岩和残积土层具遇水易软化、崩解的工程性能，在强降雨和地下水等影响下容易诱发边坡发生沿接触带近似圆弧面滑动的失稳模式。结合有限元强度折减法对8-8剖面和10-10剖面进行安全系数计算，8-8剖面计算的位移剖面图如图4所示。计算结果显示，在一般工况条件下，未进行支护的边坡安全系数达到1.354，且变形区域集中于残积土层并呈圆弧状，变形厚度约5m；8-8剖面的最大剪切应变图如图5所示，滑动面依附于残积土层底层，在坡脚处剪出，并有逐步向深部地层发展趋势。10-10剖面计算结果显示，在一般工况条件下该断面的安全系数为1.19，低于规范要求的1.30安全系数储备。图6的位移变形云图揭示了该剖面的主要变形区域集中于残积土层，呈圆弧状；变形区域厚度达5.4m，变形区域距坡顶9.2m。图7揭示了潜在滑动面整体依附于残积土层，有逐渐贯通的趋势。

结合8-8剖面和10-10剖面的计算结果，该市政边坡的失稳模式主要是依附于矽线云母片岩残积土层和全风化矽线云母片岩的接触界面的圆弧状滑动，于坡脚处剪出；整个滑动体的厚度约5m，滑动体后缘距坡顶临空面约7～9m。两个剖面的计算结果显示在一般工况条件下，8-8剖面满足规范要求，但10-10剖面的安全系数储备低于规范要求，需要考虑对其进行加固。

图5 8-8剖面最大剪切应变图

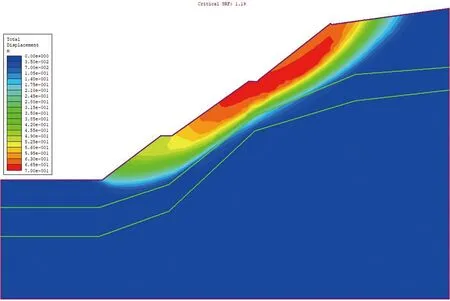
图6 10-10剖面总位移变形图

图7 10-10剖面最大剪切应变图

4 市政边坡加固设计

4.1 加固设计方案

基于前文对该市政边坡的失稳模式分析，针对该边坡潜在滑动面依附在残积土层，且滑动面深度较浅，考虑经济和场地情况，采用全粘结锚杆加固是较为经济有效的加固手段，即在坡面布设泄水孔，坡脚设置水渠，减少长期降雨引起边坡失稳的可能。具体设计方案如图8～图9所示。

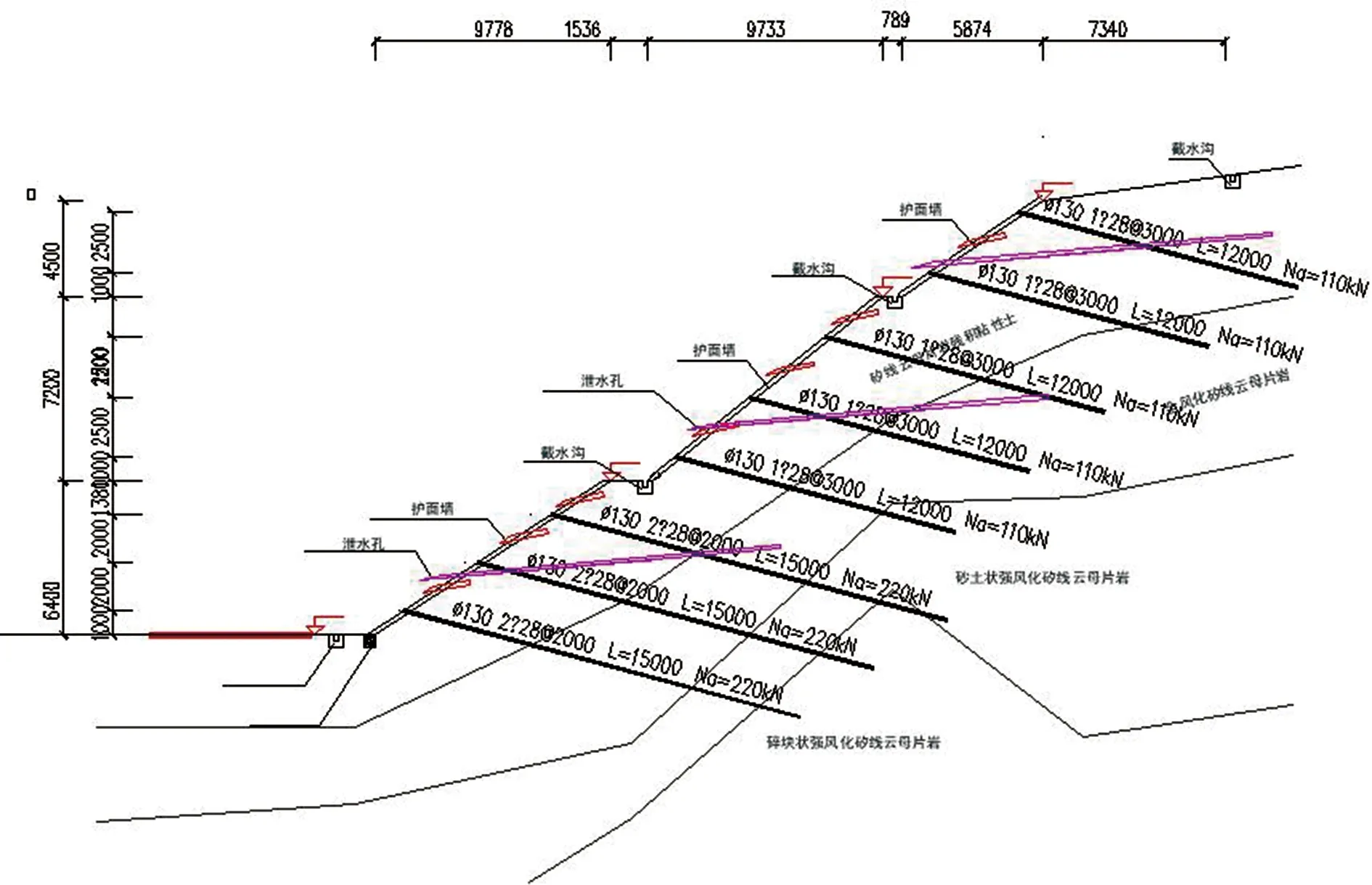
图8 8-8剖面边坡加固设计方案

图9 10-10剖面边坡加固设计方案

4.2 边坡加固后稳定性分析

在采取以锚固为主的加固措施后，锚杆类型为全粘结锚杆，对该市政边坡进行加固后边坡稳定性计算，所采用锚杆的物理力学参数如表3所示。

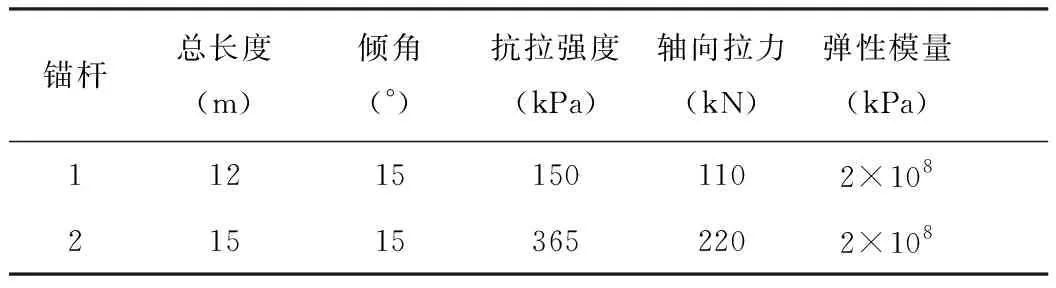
表3 锚杆物理力学参数

数值模拟得到在一般工况条件下8-8剖面的安全系数为1.452，8-8剖面的位移图和最大剪切变形图如图10～图11所示；10-10剖面的安全系数为1.34，10-10剖面的位移图和最大剪切变形图如图12～图13所示；两个剖面均达到规范的安全系数储备要求。

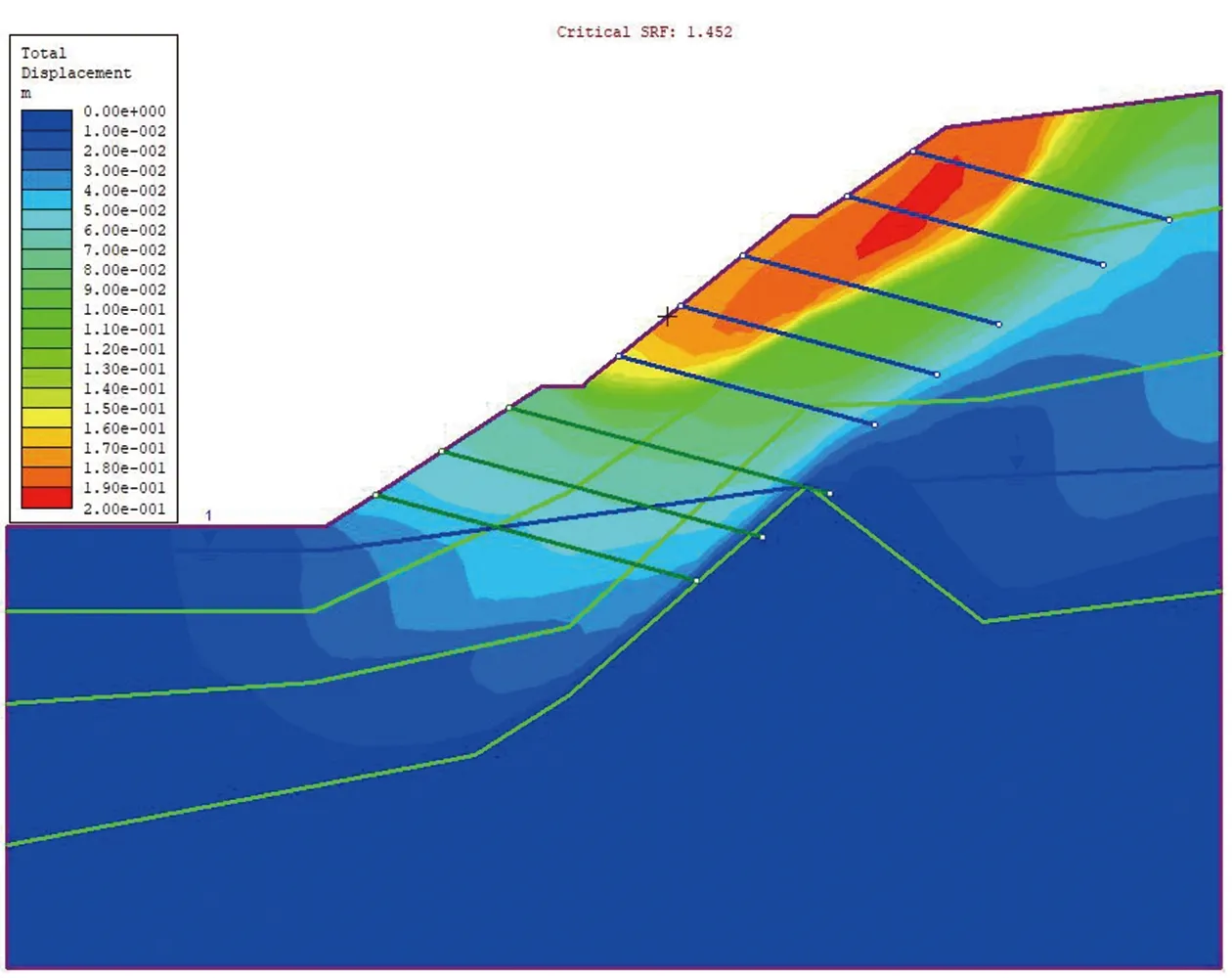
图10 8-8剖面加固后边坡总位移云图

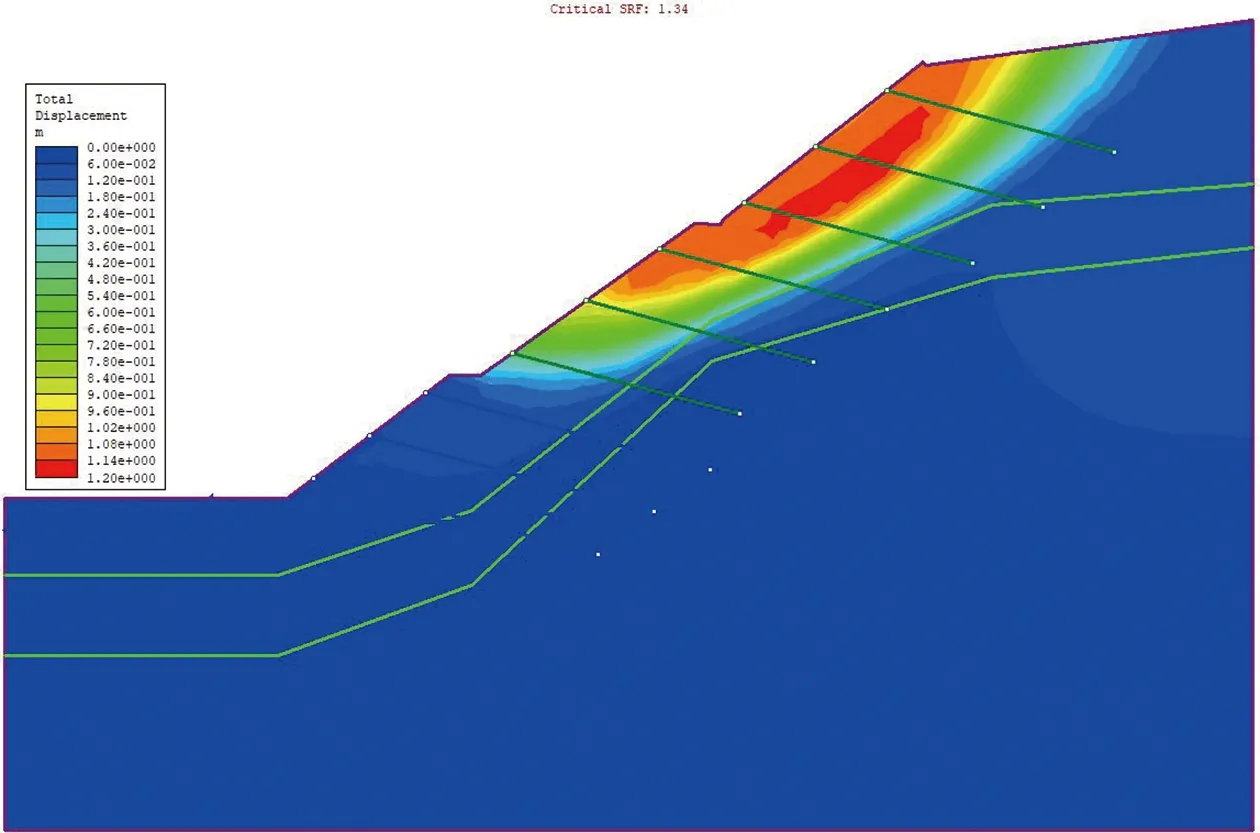
图12 10-10剖面加固后边坡总位移云图

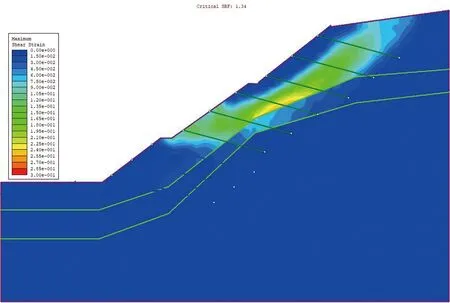
图13 10-10剖面加固后边坡最大剪切应变云图

4.3 边坡加固后的失稳模式

经过锚杆加固处理后，两个剖面的失稳模式都发生了变化。图10显示，8-8剖面在采取全粘结锚杆支护后的变形区域集中于全风化层，从浅层局部变形转变为整体滑动变形。图11显示，该边坡的主要滑动面仍然依附于残积土层，但全风化矽线云母片岩层也有部分区域有剪切应力集中，滑动面呈现浅部为主、深部发展贯通的趋势，并在坡脚处剪出。

10-10剖面在经过锚杆加固处理后表现出与8-8剖面不同的失稳模式，变形区域主要集中于上层两个台阶区域并依附于残积土层底部界面，变形范围减少。图13显示剪应变主要分布在残积土层，但滑动面有向全风化层发展的趋势。

5 结论

本研究通过对选取的两个典型剖面进行失稳模式分析，采取全粘结锚杆进行边坡加固，并基于有限元法分析边坡加固效果，得到以下两个结论。

(1)综合工程地质条件和数值模拟方法，该边坡的失稳模式是依附于矽线云母片岩残积土层底部接触界面的圆弧状滑动。

(2)采用全粘结锚杆加固方案，该边坡稳定性大大提高，潜在滑动面从加固前的坡脚处剪出，转变为以上一台阶为剪出口，使边坡从整体性滑动转为局部小区域的滑动。