基于Copula函数的抚河流域廖坊与洪门水库丰枯遭遇分析

刘沁薇

（江西省水文局，江西 南昌330009）

0 引言

抚河位于江西省东部，为江西省第二大河，是鄱阳湖水系主要河流之一，域内现有廖坊与洪门两座大型水库，其供水情况支撑着抚河流域城乡生活、生产及生态用水安全。近年来，两大水库已在实际工作中逐步实施联合调度，但目前依然缺乏系统的技术支撑，而全面掌握其入库流量丰枯遭遇特性，将有利于水利管理部门更好开展水库调度工作。作为在目前研究变量相关性领域运用较为灵活的方法，Copula函数在多种水文事件分析中愈加受到重视[1，2]，在径流丰枯遭遇分析领域也有较多应用，刘祖发等[3]利用Copula函数构建了东江流域3大水库的联合分布，获得了各水库在特定概率下入库流量的可能组合，石卫等[4]构建了Copula联合分布模型并分析了三峡工程与天然径流量丰枯遭遇特性与变化规律，丁志宏等[5]构造了南水北调西线一期工程调水区径流与黄河上游来水之间的联合分布并分析其丰枯遭遇频率，可为工程实施提供参考依据。鉴此，本研究基于廖坊与洪门水库入库流量资料，使用Copula函数构建二维联合分布并分析其丰枯遭遇特性，以期为抚河流域水库群联合优化调度提供一定的决策依据与支撑。

1 研究区域概况及资料

1.1 研究区域概况

廖坊水库是一座以防洪、灌溉为主，兼顾发电、供水、航运等综合利用的大（二）型水库，总库容4.32亿m3，位于抚河干流中游，距离抚州市45km左右，地处洪门水库与南城水文站所处支流汇合处下游，控制流域面积7 060km2。洪门水库是一座以发电为主，兼顾防洪、灌溉等的大（一）型水库，总库容12.14亿m3，位于抚河主要支流黎滩河下游，经黎川县至南城县汇入抚河干流，距南城县洪门镇上游2km处，控制流域面积为2 376km2。

1.2 资料

本研究选取廖坊水库2006～2018年、洪门水库1952～2018年入库流量资料，在经还原分析后[6]，因廖坊水库仅有2006年下闸蓄水后的资料，故将廖坊水库入库流量序列与廖家湾水文站2006～2018年流量序列建立相关关系并进行延长，廖家湾水文站位于廖坊水库下游40km处，为抚河中游控制站，控制流域面积为8 723km2，图1位廖家湾水文站与廖坊水库多年月平均流量相关图，经检验相关性较高，经资料延长后以此得到廖坊与洪门水库在1952～2018年间三大时间尺度（全年、汛期、非汛期）的入库流量序列。

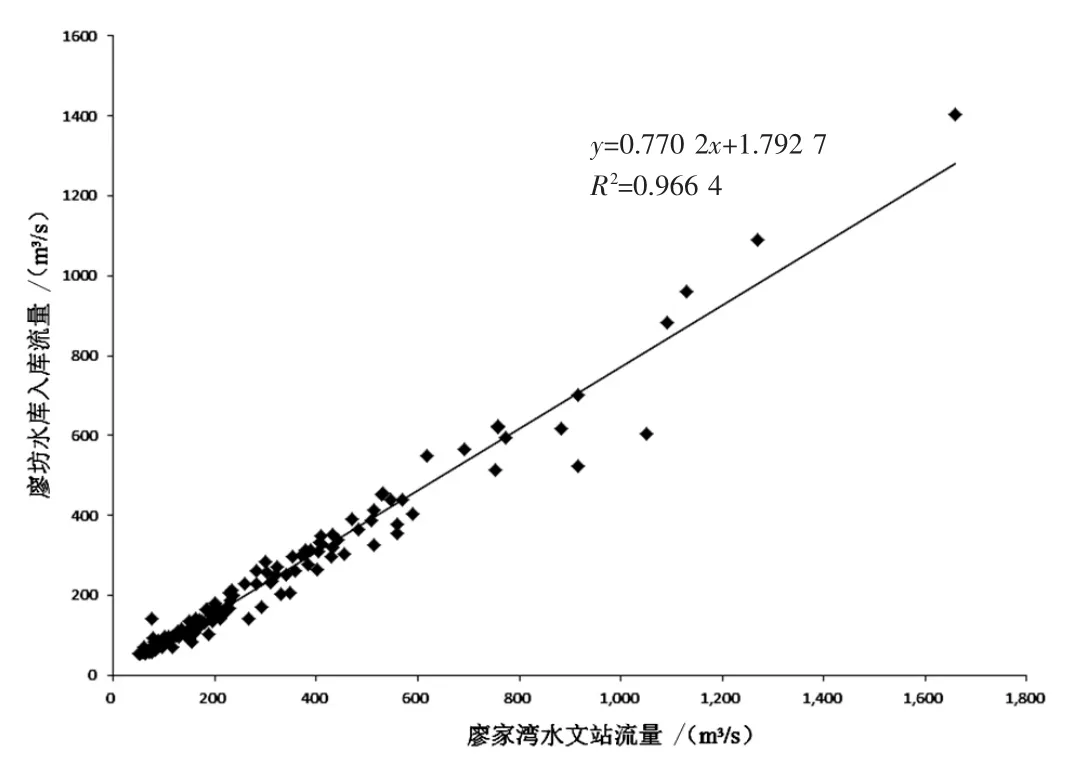
图1 廖坊水库与廖家湾水文站多年流量相关关系图

2 研究方法

2.1 Copula函数

1959年，Sklar提出Copula理论[7]，其基本形式为：设X，Y为连续的随机变量，Fx和Fy分别为其边缘分布函数，X和Y的联合分布函数为F（x，y）。若Fx和Fy连续，那么存在唯一的Copula函数Cθ（u，v）满足：

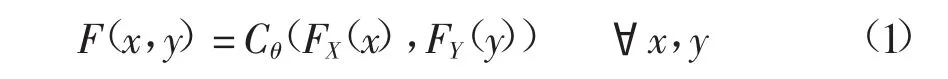
式中，θ为待定参数，Copula函数可分为二次型、椭圆型和Archimedean型3种类型。

2.2 确定边缘分布函数

本研究选取皮尔逊Ⅲ型（P-III）分布、广义极值（GEV）分布和对数（LOGN）正态分布对变量进行拟合，KS检验[8]评价分布的可行性，均方根误差（RMSE）法[9]检查拟合程度，并根据AIC信息准则[10]确定出最优的边缘分布。

假设有样本X，n为样本大小，F（nx）i为其经验分布，则KS检验的计算公式：

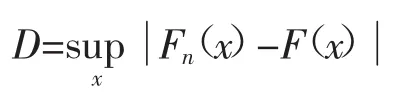
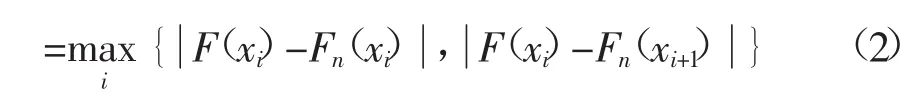
若D大于临界值Dc，则拒绝该假设。

RMSE计算公式：

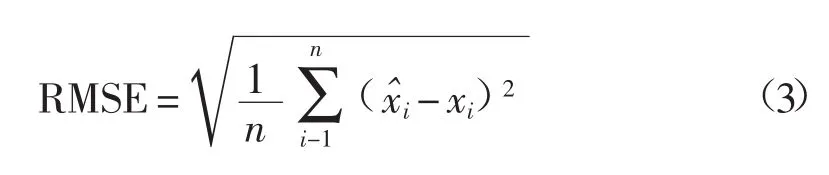
AIC计算公式：

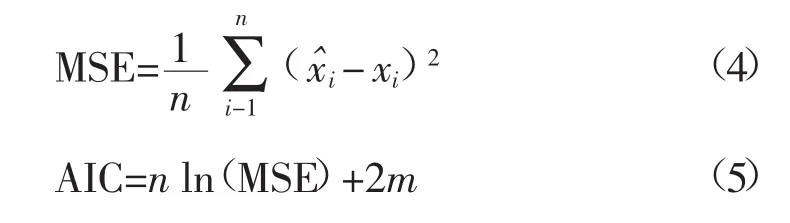
式中，m为分布函数参数个数，AIC越小，则拟合效果越好。

2.3 Copula函数参数估计与优选

Copula函数通常采用适线法、非参数估计法和极大似然法[11]来进行参数估计，Clayton、Frank与Gumbel-Hougard为3种常用的Archimedean型Copula函数[12]。AIC信息准则法与离差平方和准则法（OLS）常用于对Copula函数进行拟合优选，AIC计算公式见式（5）。

OLS的计算公式：

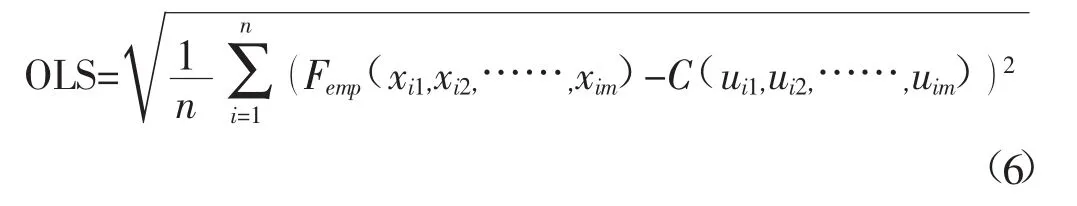
式中，n为样本个数；m为模型维数；k为参数个数；Fem（pxi1，xi2，……，xim）、C（ui1，ui2，……，uim）为样本的经验频率和理论频率。

2.4 丰枯遭遇

本研究按丰、平、枯三级对入库平均流量对应频率进行划分，X≤25%为丰水年，25%＜X＜75%为平水年，X≥75%为枯水年，可将两大水库丰枯遭遇分为以下9种情况：①丰-丰型；②丰-平型；③丰-枯型；④平-丰型；⑤平-平型；⑥平-枯型；⑦枯-丰型；⑧枯-平型；⑨枯-枯型。

3 结果及分析

3.1 确定边缘分布函数

在三大时间尺度上，分别对廖坊与洪门水库进行3种边缘分布（P-III分布、GEV分布和LOGN正态分布）的拟合检验，见表1。根据拟合结果，三种边缘分布的DK-S值均小于临界值Dc（0.1644），即3种分布在三大时间尺度上均通过了KS检验。对于廖坊水库，在三大时间尺度上P-III分布的DK-S、RMSE与AIC值均最小，故P-III分布的拟合效果最优；对于洪门水库，在汛期和非汛期两大尺度上P-III分布的拟合效果最优，在全年尺度上P-III分布的RMSE与AIC值最小，GEV分布的DK-S值最小，而鉴于P-III分布与GEV分布的DK-S值相差很小，且P-III分布在我国水文频率分析计算中运用较为广泛，经分析考虑选取P-III分布作为最优边缘函数。综上，两大水库在三大时间尺度上均选取P-III分布作为最优边缘分布函数进行丰枯遭遇分析。

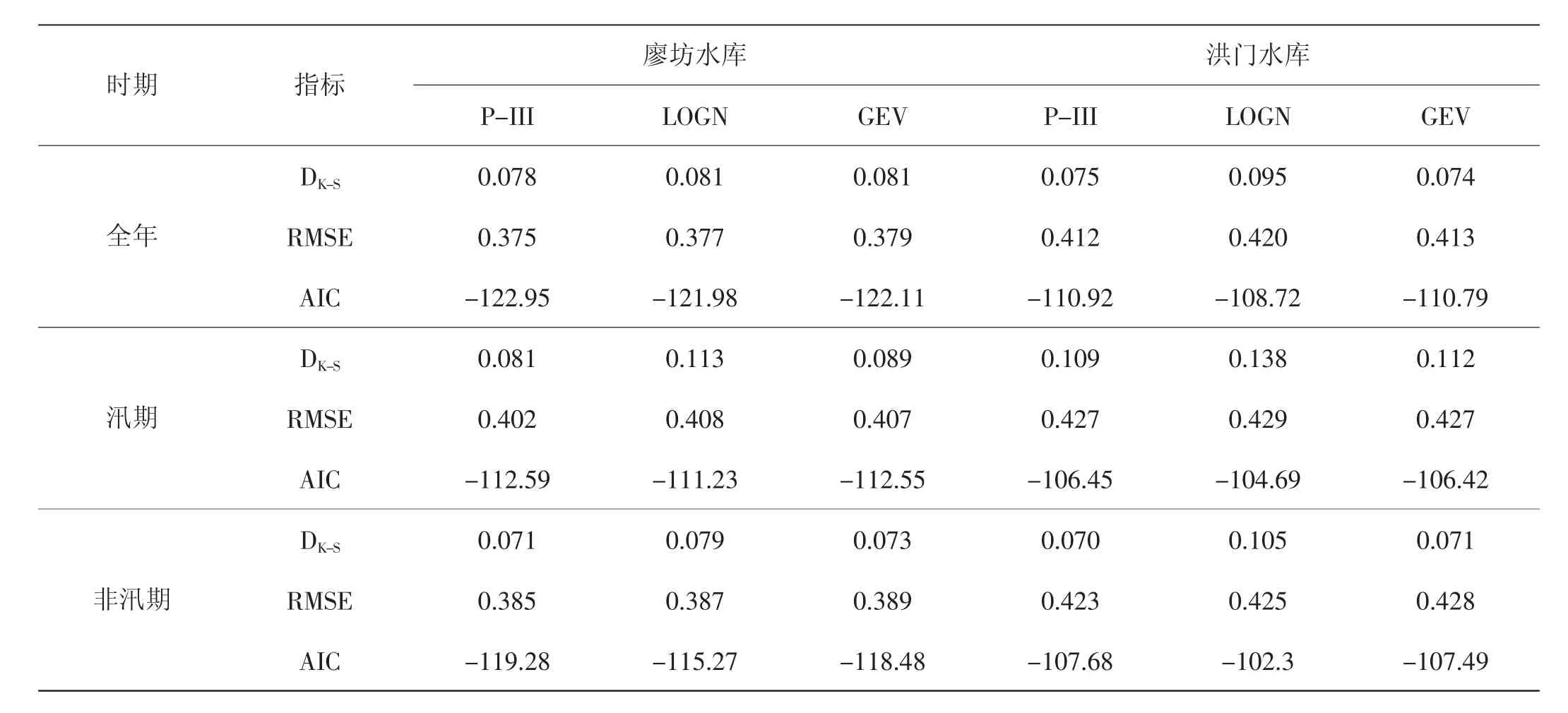
表1 廖坊与洪门水库入库流量边缘分布拟合检验结果

3.2 确定最优Copula函数

本研究选取Gumbel、Clayton与Frank三种 Copula函数进行拟合对比分析，在对计算分布与经验点据比较后，发现3种函数的拟合度均较高，为选择适应度最优的Copula函数，则需进一步采用AIC信息准则法与离差平方和准则法（OLS）进行拟合优选，结果见表2。由计算结果可知，在三大时间尺度上Clayton Copula函数的AIC和OLS值均最小，故选择该函数作为本次研究的连接函数。

3.3 两大水库丰枯遭遇分析

根据已选取的Clayton Copula函数对廖坊与洪门水库开展丰枯遭遇分析，根据设定的丰枯划分标准，可将9种丰枯遭遇情况分为丰枯同步（同丰、同平、同枯）与丰枯异步（丰-平、丰-枯、平-丰、平-枯、枯-丰、枯-平）两种情况，由于 Copula函数具有对称性，丰-枯与枯-丰、丰-平与平-丰、平-枯与枯-平的概率相等。从有利于水库调度的角度分析，枯-枯遭遇是在调度分析中应避免的情形，即为对调度不利的情形。具体计算结果见表3。

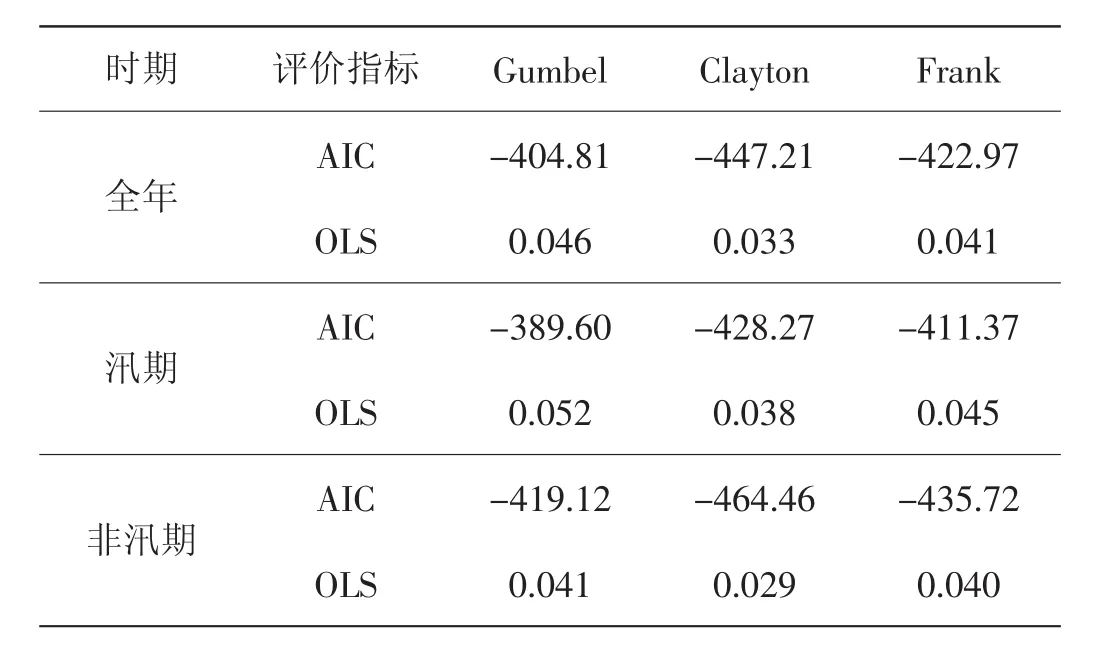
表2 Copula函数的拟合优度检验结果

分析表3可以得到如下结论：（1）在三大时间尺度（全年、汛期、非汛期）上，因为廖坊与洪门水库地理位置较为接近，丰枯特性基本类似，丰枯同步频率（80%～85%）远大于丰枯异步频率（15%～20%），其中在非汛期尺度上丰枯同步频率最高（84.74%），说明两大水库来水同步性较高，在同丰、同平丰枯遭遇组合时开展对抚河流域的联合梯级调度是有利的；（2）在丰枯同步情形中，同平的频率（40%～42%）最高，大于同枯的频率（22%～25%）与同丰的频率（17%～19%），说明两大水库在所有丰枯遭遇组合中同为平水年的可能性最大；（3）在丰枯异步情形中，三大时间尺度上丰-枯与枯-丰组合的遭遇都接近于零，进一步说明两大水库来水同步性较高，几乎不可能发生来水情况完全相反的情况；（4）在三大时间尺度两大水库同枯的频率为22%～25%，而在非汛期尺度上同枯的频率最高（24.68%），故在实际调度过程中，尤其是非汛期更应兼顾两大水库丰枯同步性。

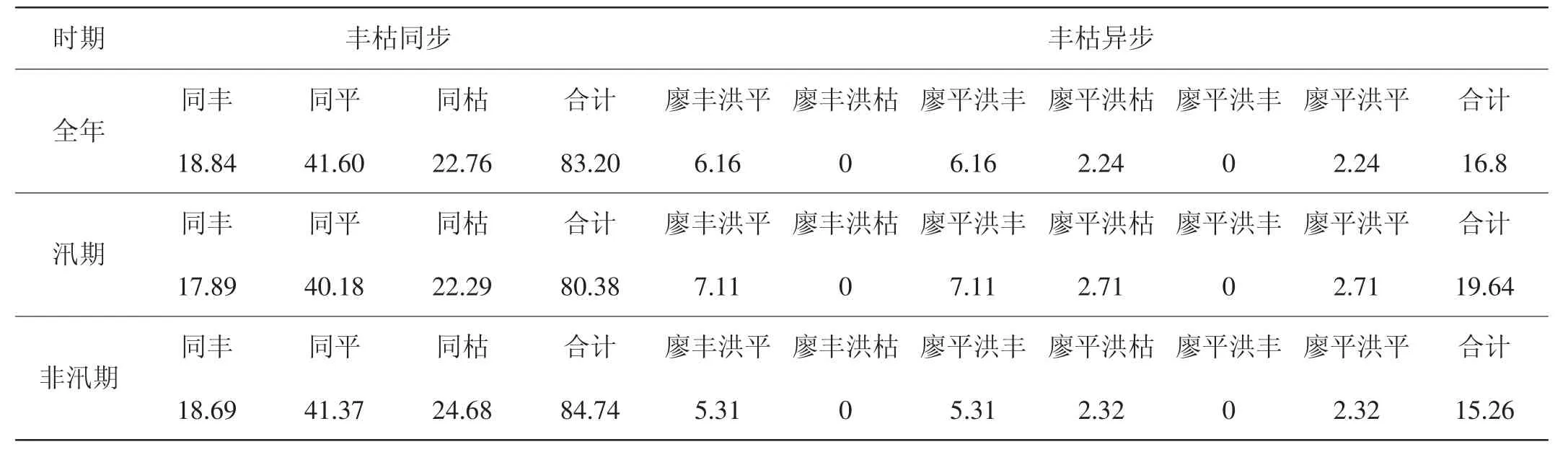
表3 廖坊水库与洪门水库入库流量丰枯遭遇表 %

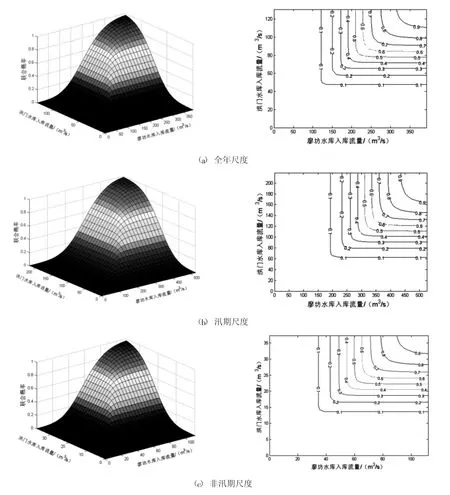
图2 两大水库入库平均流量在三大时间尺度上丰枯遭遇联合分布（左）与等值线图（右）

图2为三大时间尺度上两大水库丰枯遭遇联合分布与等值线图，可为抚河流域调水提供决策支持。

4 结论

（1）在全年、汛期、非汛期三大时间尺度上，抚河流域两大重要水库——廖坊与洪门水库的丰枯遭遇特性基本类似，丰枯同步的频率均在80%以上，丰枯组合的频率接近于零，来水情况完全相反几乎不可能发生。

（2）两大水库在非汛期尺度上同枯的频率最高，故在实际调度过程中，尤其是枯水年份应特别兼顾其丰枯同步性。

（3）本研究成果可为抚河流域水库群联合调度提供一定的理论依据，并可在江西省境内跨流域调水中进行深一步的研究。