核电厂数字化仪控系统软件可靠性定量评估研究

黄 奇，张 庆，刘明星，王远兵，钟 科

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

随着计算机技术的发展，改造与新建的核电厂逐步采用数字化仪控系统实现反应堆的保护和控制功能，数字化仪控系统的安全性和可靠性是核电厂平稳运行的关键。目前国内外对于数字化仪控系统硬件方面可靠性研究已取得了较大成就，然而对于数字化仪控系统软件可靠性评估方面的研究基本还处于初始启蒙状态。

标准IEEE std 1633中将软件可靠性评估模型分为3种通用类别，即呈指数分布的非齐次泊松过程模型(NHPP)、非指数分布的NHPP模型和贝叶斯模型。而Schneidewind模型是标准IEEE std 1633中推荐的一种呈指数分布的NHPP典型模型。由于该模型有一个基本思想，即部分测试周期中检测的错误率受某些客观因素影响，不能更好地对软件未来的可靠性进行预计。

该模型有以下三种形式：模型1—利用n个时间单元中的所有错误计数。其基本出发点是所有数据点都同样重要；模型2—忽略从第一个到第s-1个时期的错误数，即只使用从第s个时期到第n个时期之间的数据。其基本出发点是早期数据对预计未来行为作用很小；模型3—使用从周期1到s-1的累积错误计数，作为第一个数据点，而使用s到n的独立错误计数作为其他数据点。此方法介于前两个模型之间，反映了以下思想：前s-1个周期的数据组合可以预计以后阶段的失效率。

本文结合IEEE std 1633标准中Schneidewind模型，以核电厂数字化仪控系统为研究对象，研究数字化仪控系统软件可靠性的分析方法，并结合某堆型核电厂数字化仪控系统典型功能模块的软件故障数据进行研究。

1 Schneidewind模型构造

在利用该模型进行研究时，需进行以下假设：

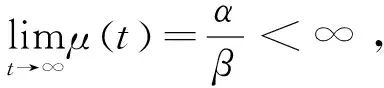
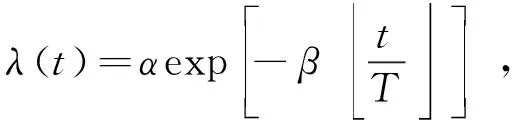
(3)每个时间间隔检测出的错误数是相互独立的；

(4)软件运行方式与预期的运行使用方式相似；

(5)每个错误出现的机会相等，且各错误的严重程度相同；

(6)软件的失效是相互独立的；

(7)观测软件的时间间隔都相同。

根据假设，第i个时期的累积错误数均值为：

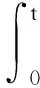
(1)

因此第i个时期的期望错误数为：

(2)

由于每个时间间隔检测出的错误数fi为可独立非均匀泊松随机变量，可构建似然函数如下：

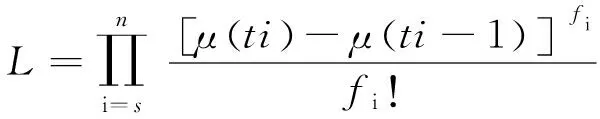
(3)

利用极大似然估计，可以得出三种模型的参数α，β的估计值。

(1)模型1

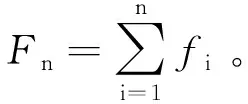
(2)模型2

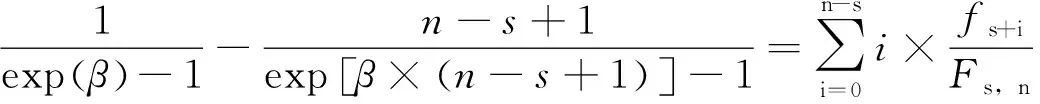
(3)模型3

2 数字化仪控系统软件可靠性评估

根据某堆型核电厂数字化仪控系统典型功能模块的软件可靠性故障数据，以“周”为测试周期，对故障数据进行统计表1所示。

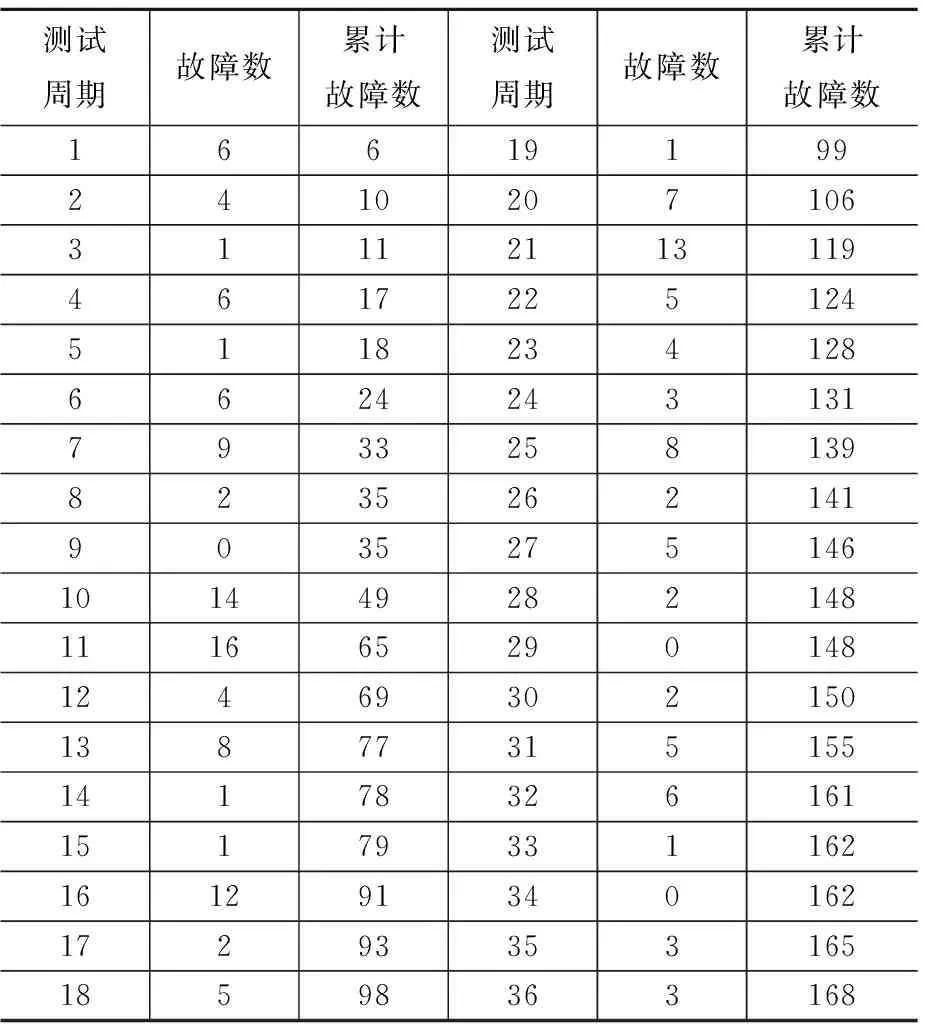
表1 故障数据统计(36周)Table 1 Fault data statistics(36 weeks)

从表1可以看出，该典型模块功能软件经过36个周期的测试，共发现168个故障。测试初期，故障发现率较高，随着测试不断深入，发现的故障不断修复，通过测试发现的故障数量同比有所减少。从统计结果可以看出，数据满足假设条件中任一周期期望的错误发生数与此周期的期望未检测出的错误数成正比例的假设条件。

2.1 参数估计

根据软件故障数据统计结果，将36周数据代入到第2章构建的模型1中，对参数α和β进行估计，得到估计值为：

α=6.386 419 403 300 72

β=0.018 446 464 462 79

参数α也称为其初始失效强度。

2.2 软件可靠性评估

累计失效数的计算公式如式(1)所示，通过对实际数据以及估计后拟合的曲线作图如图1所示。

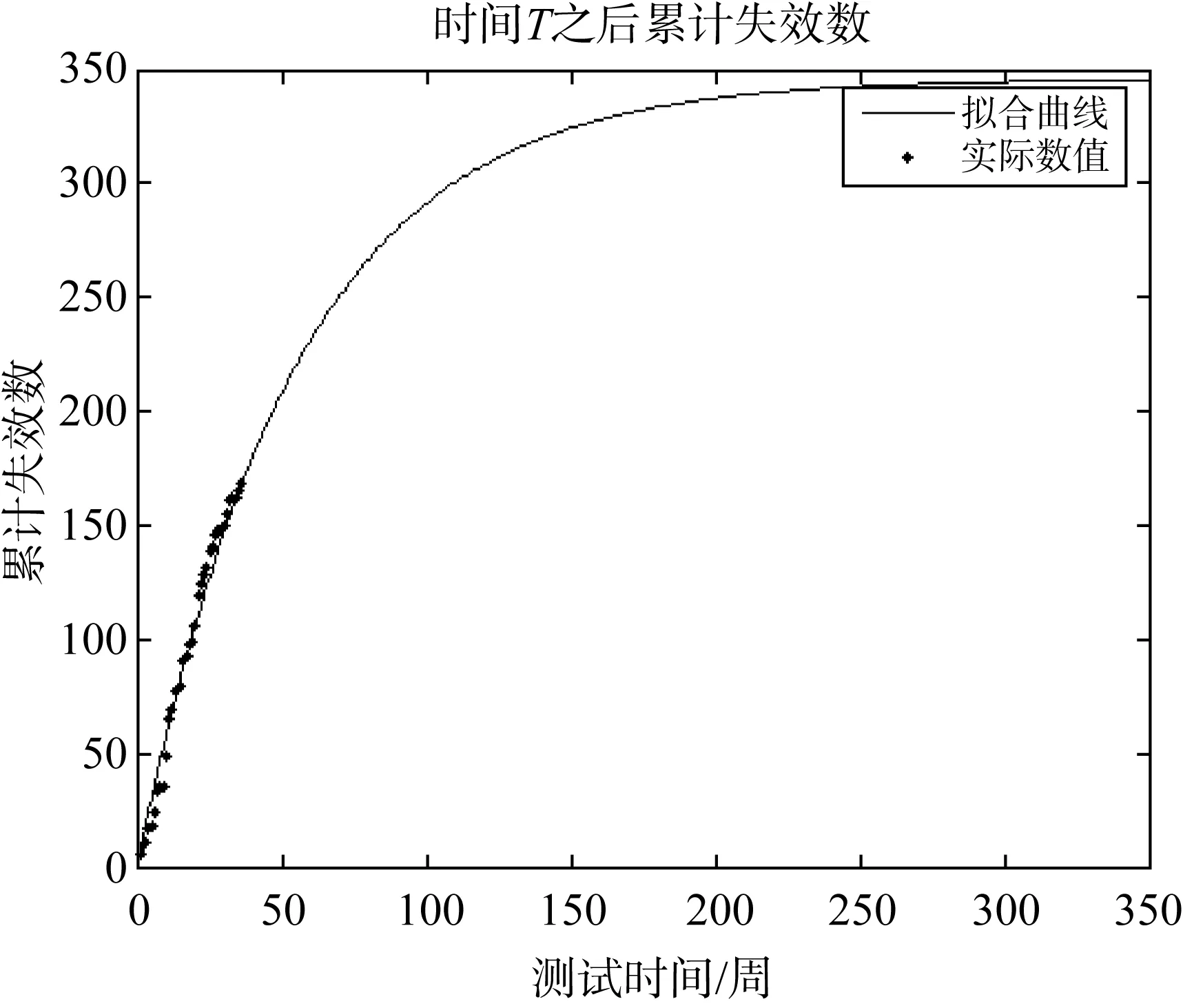
图1 累计失效数随测试时间的变化曲线Fig.1 Variation curve of cumulativefailure number with test time

根据实际数据以及估计拟合的结果，可以得到数据方差MSE为：

MSE=65.75

残余失效数的计算公式如式(4)所示：

(4)

通过该模型得到的软件可靠度是一个分段过程，用R(tn+Δt)表示，其计算公式如式(5)所示：

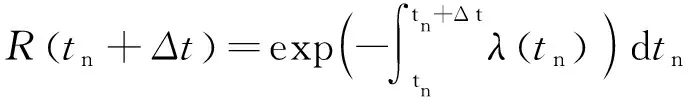
(5)

并且可以计算得出此时当测试周期为36时，软件残余失效数为178.2，如图2所示。同时可以得到软件可靠度随着测试时间的变化曲线如图3所示。

图2 残余失效数随测试时间的变化曲线Fig.2 Variation curve of residualfailure number with test time

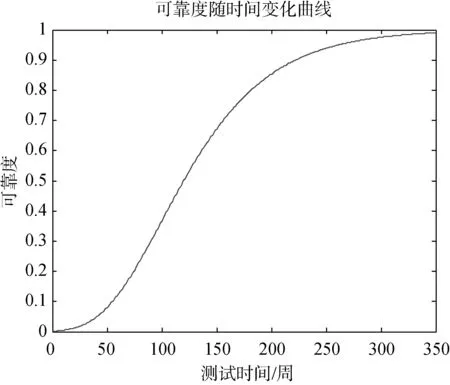
图3 软件可靠度随着测试时间的变化曲线Fig.3 Variation curve of softwarereliability with test time

从预计结果显示，软件可靠度随着测试时间趋近于指数变化形式，根据图3所示结果，目前阶段，还需要继续对软件进行测试以发现bug，从而提高软件的可靠度水平，以满足相关指标要求。

从该模型的预计计算结果显示，该模型可用于指导相关人员进行软件测试，明确何时应加大测试力量的投入、评估何时测试结束等。

3 模型评估与实际数据对比

根据上述验证结果，测试周期36时，内部存在的故障还较多，还需继续进行测试以发现bug并进行修复，进而提高软件可靠性。通过继续对软件可靠性进行测试，得到测试结果如表2所示。

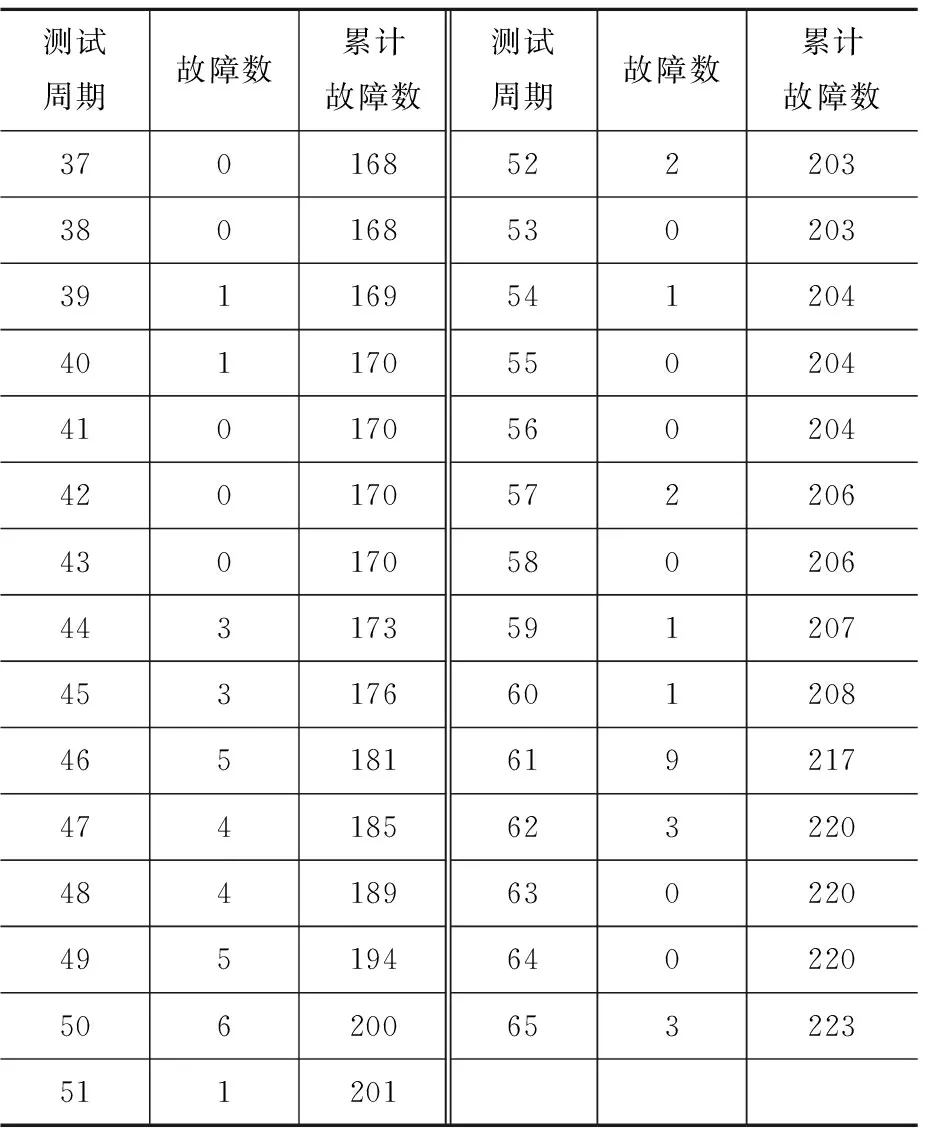
表2 故障数据统计(65周)Table 2 Fault data statistics(65 weeks)

将后续测试得到的结果与前期预期的结果进行对比，如图4所示。

图4 后续测试结果与前期预计结果对比Fig.4 Comparison of follow-up test resultswith previous expected results

根据图4对比数据显示，根据前36个测试周期得到的拟合结果基本与后续测试结果接近，但还是存在些许误差，并且从图中对比数据可以看出，随着测试周期的逐步增加，误差逐渐增大，因此在应用该模型对该堆型核电厂数字化仪控系统软件可靠性进行预计评估时，需根据实际结果对模型估计参数进行不断地迭代优化。

根据所有65周测试结果进行优化后得到的参数估计结果如下所示，优化后的曲线如图5所示。

α=6.538 934 067 655 78

β=0.022 553 308 627 75

图5 数据优化后的累积失效数曲线Fig.5 Cumulative failure number curveafter data optimization

4 总结

本文对IEEE std 1633中提到的Schneidewind软件可靠性评估模型进行研究，并结合某堆型核电厂数字化仪控系统典型功能模块软件故障相关数据，研究Schneidewind模型对于核电厂数字化仪控系统的适用性。

本文对某堆型核电厂数字化仪控系统典型功能模块的软件可靠性进行评估，计算了软件的累积故障数以及残余故障数。通过评估结果发现，目前该堆型数字化仪控系统典型功能模块的软件还存在有残余故障，将会影响该软件可靠性，还需继续对该堆型数字化仪控系统软件进行测试，发现软件bug并修复，从而提升软件的可靠性，以使其满足相关要求。

另外，应用该软件可靠性定量评估模型对核电厂数字化仪控系统软件可靠性进行定量评估时，能够很好地对软件可靠性进行拟合，但是随着测试周期的逐步增加，需根据实际测试结果，不断地对模型参数进行迭代优化，以贴近实际的结果，以利于有效地指导后续测试工作。同时，可以选择不同的典型功能模块，以实现其对整个仪控系统软件可靠性评估的覆盖性。