收缩人工蜂群算法在核动力设备优化设计中的应用

李贵敬，赵克宝

(1.燕山大学 车辆与能源工程学院，河北 秦皇岛 066004；2.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001；3.河北建材职业技术学院 信息工程系，河北 秦皇岛 066004)

由于能源危机日益严重，同时世界各国对节能减排的要求越来越严苛，因此核能具有广阔的发展空间。然而现有核电系统初投资太高，有资料表明，核电站初投资成本是火电的2.5倍左右。其中，设备成本占据了51.4%[1]。因此有必要从设备优化设计着手，降低核动力装置的初投资成本，从而提升核电系统在电力市场的竞争力。

人工蜂群算法(Artificial Bee Colony,ABC)是一种基于蜜蜂采蜜机理发展而来的群智能搜索行为的随机优化算法，在工程领域得到了较为广泛的应用[2-4]。然而，目前关于ABC的研究与应用还处于初级阶段。ABC在处理复杂优化问题时，搜索精度较低[5]。本文利用在搜索后期增强ABC收缩功能的策略，提出了收缩人工蜂群算法(Contracting Artificial Bee Colony,CABC)，提高了算法在优化后期的局部搜索能力，使算法的搜索精度和收敛速度得以改善。

1 ABC原理及改进

ABC是基于蜜蜂采蜜机理发展而来的，具有系统性、分布式、自组织性及正反馈的特点。

1.1 ABC基本原理

ABC的基本原理是根据蜂群搜索食物源的过程来搜索最优设计方案的。总蜂群由引领蜂、跟随蜂及侦察蜂组成。搜索的形式分为三部分：首先，在给定的可行域空间内由引领蜂搜索食物源(优化问题设计方案)，并记录该食物源的品质、数量，即设计方案的适应度。随后，跟随蜂根据引领蜂所提供的适应度评定信息，确定跟随哪个引领蜂到其所搜索到的食物源采蜜，即在该引领蜂所指定的设计方案周围进行小范围搜索，设计方案被选中的选择概率取决于其适应度的大小。此外，当某个设计方案周围经过引领蜂及跟随蜂的多次搜索之后，如果没有搜索到新的更好的设计方案，则由侦查蜂随机搜索新设计方案。引领蜂和跟随蜂对食物源位置更新公式为：

(1)

式中：vij——第i个设计方案的第j个变量经引领蜂和跟随蜂搜索后的新位置；

xij、xkj——随机选取的两个设计方案(第i个及第k个设计方案)的第j个变量；

rij——是[-1,1]范围内随机选取的随机数。

1.2 算法的实施及改进

ABC的进化方式采用随机选取的食物源(设计方案)信息，通过随机进化得到新的食物源位置，因而算法的随机性、盲目性较强，对最优设计方案的搜索精度不高。结合自主开发的收缩策略及现有ABC的实现技术，提出了收缩人工蜂群算法(CABC)，算法逻辑框图如图1所示。

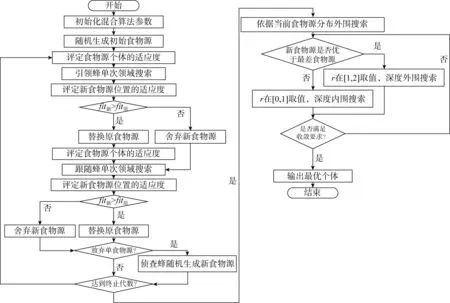
图1 CABC逻辑框图Fig.1 Logic diagram of CABC

(1)收缩策略

在设计空间，以ABC进化所得食物源(设计方案)分布为基准，向品质最差的食物源的反向立体方向搜索。首先向食物源分布边界以外的范围，实现最大限度的逐步搜索，根据搜索到的食物源品质，调整搜索步长。如在多次调整搜索步长后，均未搜索到品质优于最差食物源的新食物源，则外围搜索失败。调整为内围最大限度逐步搜索，对搜索步长实现反馈调整机制，直至搜索到优于最差食物源的新食物源，取而代之。具体收缩的实施为：

(2)

式中：xcj、xhj——表示收缩策略得到的新食物源、最差食物源(设计方案)的第j个变量。

第一步收缩，r取[1,2]的随机数。分两种情况：

1)如果收缩得到的新食物源优于最差食物源，则r的取值区间不变，仍为[1,2]，重新随机取值进行深度外围搜索。最终，用该立体方向最大限度外围搜索到的最佳食物源替换最差食物源。

2)如果收缩得到的新食物源劣于最差食物源，则r的取值区间改为[0,1]，进行深度内围搜索。最终，用最大限度内围搜索到的最佳食物源替换最差食物源。

r的取值范围是基于两方面确定的，一方面是参考复合形算法的搜索系数；另一方面是由试算经验确定。重复上述过程，对每次更新得到的食物源分布中的最差食物源进行改良，最终整体食物源分布收敛至全局最优食物源，CABC算法搜索结束。

(2)适应度标定

基本思想是：用罚函数法适当接受生成的不可行解，丰富基因库的多样性，同时降低不良基因被遗传到后代的概率。第i个食物源的适应度函数fiti定义为：

(3)

(4)

式中：Xi——第i个食物源向量；

f(Xi)——第i个食物源的目标函数值；

gj(Xi)——第i个食物源的第j个约束函数；

cj——惩罚权重系数。

(3)选择概率

人工蜂群算法中跟随蜂对食物源的选择，是通过观察完引领蜂的摇摆舞来判断食物源的收益率，并依据收益率大小来选择到哪个食物源采蜜。收益率通过适应度值来表示，选择概率按照公式(5)确定：

(5)

2 CABC性能测试

选取典型基准测试函数Ackley函数，测试CABC算法的优化性能，Ackley函数如公式(6)所示。CABC算法主要参数的初始化设置如表1所示。

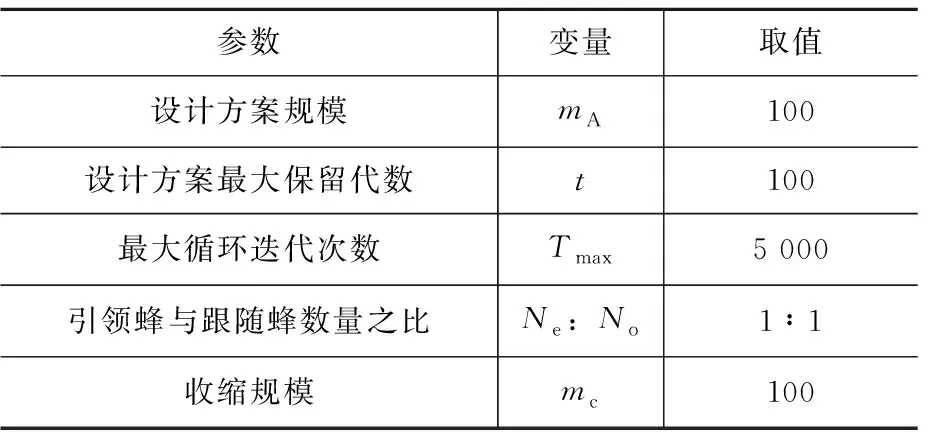
表1 CABC算法参数设置

对选取的优化测试函数公式(6)进行30次连续独立优化运算，综合对比CABC与IABC算法[5]、标准ABC算法、GABC算法[6]、RABC算法[7]及TABC算法[7]的性能，结果如表2所示。

(6)

全局最小点为fmin=0,xi=0,i=1,2,…,n。

表2 Ackley函数测试结果对比

Ackley函数属于多模函数，是复杂非线性全局优化测试算例。由Ackley函数的优化对比结果可见，CABC算法在30次连续独立优化运算所搜索到的最优输出值中，其最佳值、最劣值、平均数值及标准方差值，均明显优于IABC、ABC、GABC、RABC及TABC算法，说明CABC算法对全局最优解的搜索精度及算法的鲁棒性都明显优于其他对比算法。

选取维数n=30Ackley测试函数，对比分析CABC、IABC、ABC、GABC、RABC、TABC算法的收敛性，如图2所示。

图2 CABC、IABC、ABC、GABC、RABC和TABC算法对Ackley函数的收敛曲线Fig.2 The convergence curves of CABC,IABC,ABC,GABC,RABC and TABC algorithmsfor Ackley function

CABC算法在对Ackley函数(n=30)的寻优过程中能够快速收敛，此外，在相同进化代数下平均最佳值大幅度低于其他算法，CABC表现出良好的搜索收敛性能。CABC算法的整体进化趋势与其他算法截然不同，即在进化起始阶段(小于5000进化代)，CABC算法便能够快速收敛至约1×10-13，与全局最小点的差距极小，随后进化更新速度下降，可认为在小于5000进化代时，算法已收敛。而IABC、ABC、GABC、RABC及TABC算法在104进化代内，收敛都非常缓慢，所搜索到的平均最佳值均大于10，随后收敛速度略有提高，但仍远低于CABC算法在进化初期的收敛速度。显然，测试算例的计算结果有效验证了CABC算法中所提出的收缩策略的可行性，并直观地展示了其对收敛速度的改进效果。

3 将CABC应用于核动力设备的优化设计

核动力主循环泵为反应堆冷却剂提供循环动力，是核动力装置中的重要设备之一。轴封式主循环泵的转动惯量较高，因此其在惰转瞬变工况下安全性能较好。另外，轴封式主循环泵成本相对较低，制造、维修更便捷，效率也较高，因而，轴封式主循环泵在核动力装置中得到广泛使用。本文以减小轴封式主循环泵重量为优化目标，基于CABC寻求轴封式主循环泵结构及运行参数的最佳组合。

3.1 轴封式主循环泵计算模型的建立

选取300 MW核电系统轴封式主循环泵为设计模型。轴封式主循环泵的主要设计部件包含电动机、轴、水力部件、飞轮等，其设计过程参看文献[8,9]。

3.1.1 模型假设

本文旨在满足轴封式主循环泵安全设计要求的前提下，基于对其主要设计部件的计算，估算轴封式主循环泵的重量，进而结合CABC算法实现以轴封式主循环泵重量为优化目标的优化设计。然而，轴封式主循环泵结构紧凑、设计部件多，使轴封式主循环泵优化设计计算的复杂度增加。因此在建立轴封式主循环泵的计算模型时，引入了简化条件，包括：

(1)通过与水力性能优良的泵叶片模型开展几何相似计算，获得轴封式主循环泵叶片部分结构尺寸；

(2)基于电动机模型数据的几何相似计算，确定槽型尺寸；

(3)参考母型的相关数据确定包括轴承、热屏障、轴密封组件、刚性联轴器、空气冷却器等部件的尺寸参数；

(4)对部件做规则化处理，估算其重量。

3.1.2 强度校核

以第四强度理论为基准对泵轴的安全性进行校核，若不满足安全要求，说明轴径过小，需令最小轴径取较大标准值，迭代设计过程，直至满足安全校核要求。

安全校核条件为

(σs/σd)≥[c]

(7)

式中：τa、σa、σs——为泵轴剪切应力、拉应力及泵轴材料的屈服应力，kg/m2；

σd——折算应力，kg/m2，

[c]——给定安全系数。

在校核计算中，估算运行状态下所产生的轴向力Fa(N)为

(8)

式中：H——轴封式主循环泵扬程，m；

Dh、Dsm——轮毂直径和叶轮密封环直径，m；

Cfa——计算系数；

ρ——主冷却剂泵内流体的密度，kg/m3；

nI——叶轮级数。

ASME要求核安全一级机械各部分厚度都应至少大于规定数值δA(m)为：

(9)

式中：DA——指定的涡道内部尺寸，m；

S——许用应力，MPa；

Pd——设计压力，MPa；

c——附加厚度，m。

3.1.3 重量计算

轴封式主循环泵总重量W(t)为:

(10)

式中：轴封式主循环泵总重量为各主要部件重量之和，主要设计部件包括壳体、端盖、轮毂、泵轴、电动机、飞轮、叶片及导叶。

3.2 计算模型评价结果

将轴封式主循环泵计算模型的评价结果与母型数值进行对比，检验计算模型结果的可靠性，对比结果如表3所示，参数数值采用基于母型数据的归一化处理。

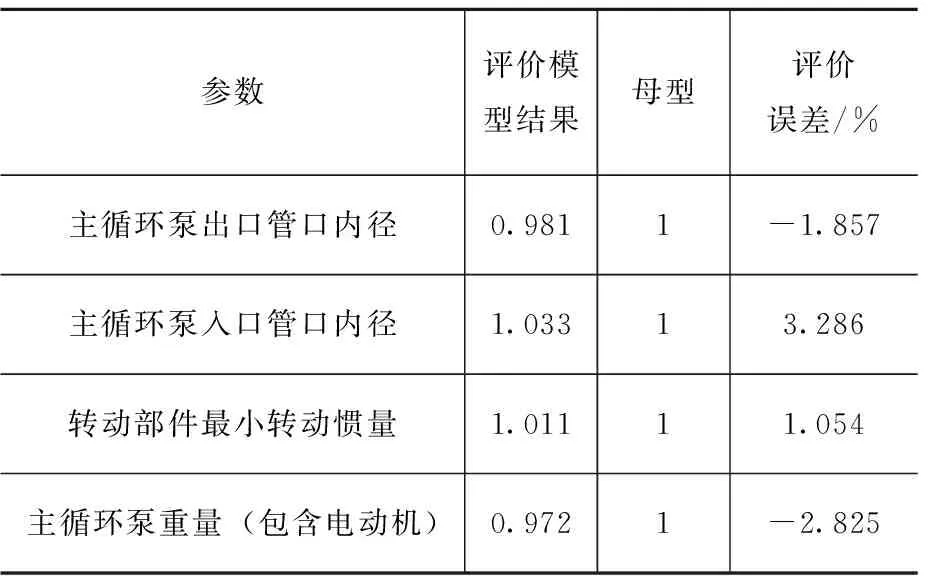
表3 轴封式主循环泵评价结果与母型参数对比

为降低优化设计计算的复杂度，引入简化假设，建立轴封式主循环泵计算模型，因此计算模型结果存在计算误差。对比结果显示：误差绝对值小于3%，在优化计算可接受的精度范围内。

3.3 优化约束条件

轴封式主循环泵优化实例研究需满足给定的设计规范、性能需求，其中包括稳态及瞬态性能。具体约束参数见表4，参数数值采用基于母型数据的归一化处理。

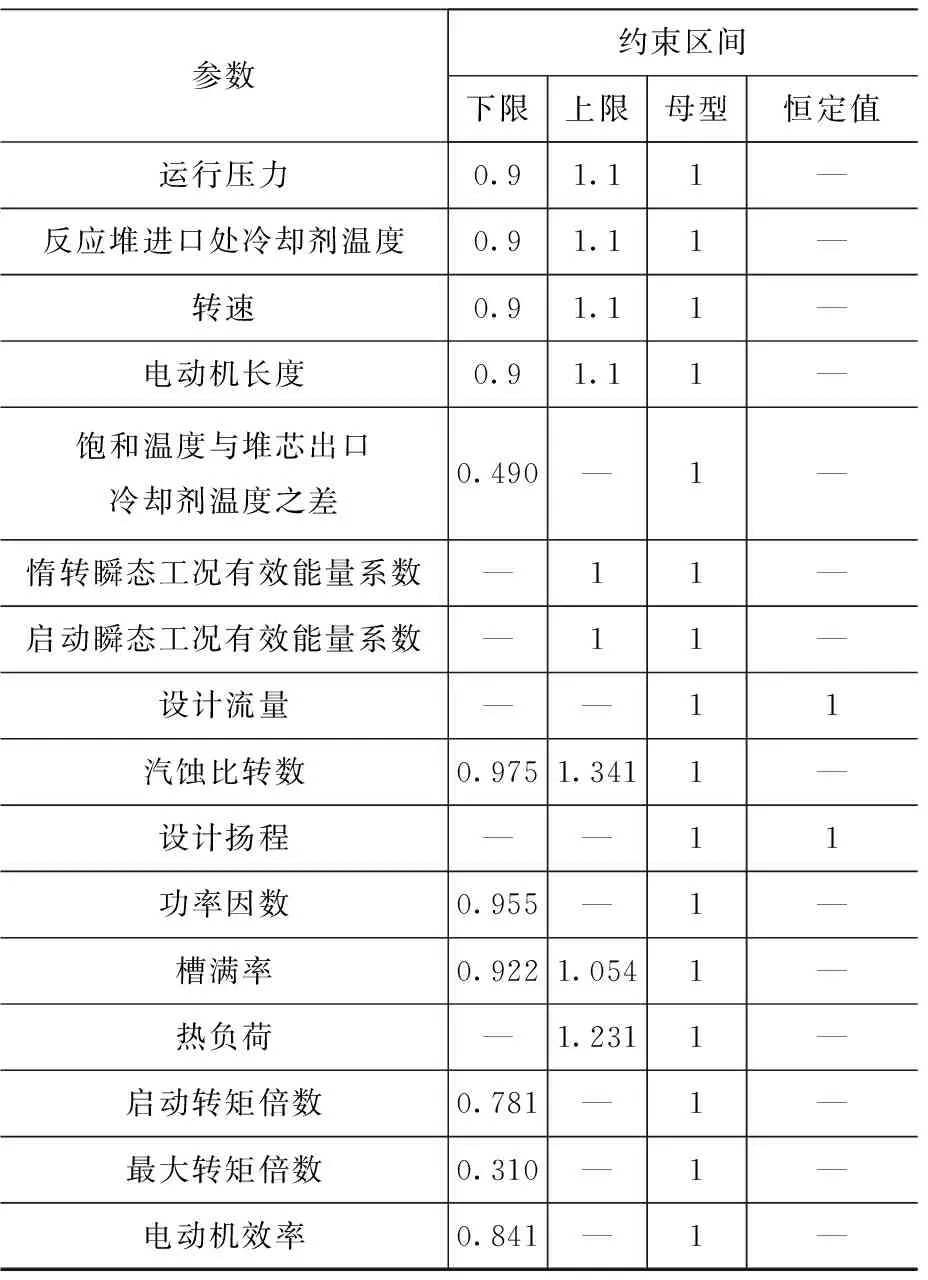
表4 约束条件限制

优化约束条件相关说明如下：

(1)约束轴封式主循环泵的设计变量，运行压力prc(MPa)、反应堆进口处冷却剂温度trc(℃)、转速n(r/min)、电动机长度Lm(m)的寻优区间；

(2)对压水堆堆芯出口处冷却剂温度数值加以约束，以保障堆芯出口处冷却剂不发生相变；

(3)降低轴封式主循环泵惰转有效能量系数、启动有效能量系数，可放缓瞬变过程的流量、转速变化速度，系统瞬态安全性增强[10,11]，因此约束惰转有效能量系数、启动有效能量系数低于相应母型数据；

(4)按照稳态设计要求，约束轴封式主循环泵设计流量、设计扬程保持恒定，与母型数据一致；

(5)为保证轴封式主循环泵的汽蚀性能处于安全且高效的范围内，约束汽蚀比转数在理想的区间内；

(6)应保证电动机的设计运行性能优良，约束其主要性能参数的限值区间，包括电动机功率因数、槽满率、热负荷、启动转矩倍数、最大转矩倍数、效率。

3.4 实例优化结果

基于CABC优化轴封式主循环泵的重量，最佳方案列于表5中。

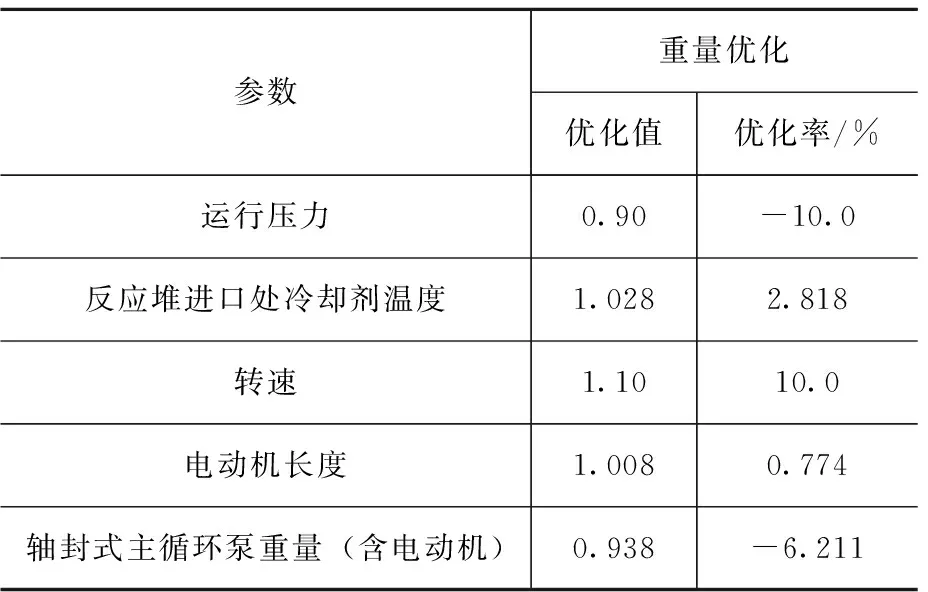
表5 轴封式主循环泵重量优化结果

实例优化结果表明：300 MW核电系统轴封式主循环泵的最优设计方案中，最优重量比母型评价程序计算结果轻6.211%，轴封式主循环泵重量优化效果显著。需注明：优化结果对比数据中，重量归一化处理是以母型计算模型的结果数据作为基准，因而优化结果数值不包含计算模型的结果计算偏差，即与母型数据的对比偏差。对优化方案加以说明(见表6)，相关分析可在一定程度上对优化方案的合理性给予理论支撑。

分析结果显示：降低运行压力有助于减轻轴封式主循环泵重量，但是可能会增加压水堆堆芯安全隐患，最优方案中通过适当降低反应堆进口处冷却剂温度，从而达到中和运行压力变化所带来的负面影响的目的。

表6 轴封式主循环泵优化结果分析

综上所述，本文将自主改进的CABC应用于以减轻轴封式主循环泵重量为优化目标的优化设计中，结果显示轴封式主循环泵独立设计参数的优化组合可使其重量减轻，从理论上给出能够使轴封式主循环泵重量减轻的参数变化方向，可为轴封式主循环泵及核动力系统的设计提供理论参考。

4 结论

本文结合自主开发的收缩策略及现有ABC的实现技术，提出了收缩人工蜂群算法(CABC)。典型测试函数的优化结果证明，CABC较其他对比算法具有更佳的搜索速度和精度。并基于CABC实现了轴封式主循环泵重量的优化设计，得出结论：

(1)CABC利用在搜索后期增强算法收缩功能的策略，提高了算法在优化后期的局部搜索能力，使算法的搜索精度和收敛速度得以改善。

(2)对典型测试函数Ackley函数的测试结果表明，CABC算法对全局最优解的搜索精度及算法的鲁棒性都明显优于IABC、ABC、GABC、RABC及TABC算法，同时其收敛曲线的下降速率远高于其他对比算法，具有更快的收敛速度；

(3)将CABC应用于轴封式主循环泵重量的优化设计研究，在给定约束条件下，轴封式主循环泵最优重量相比母型数据减轻了6.211%，效果显著。

(4)优化设计过程尚未涉及工程中的实际影响因素，仅为轴封式主循环泵设计工况方案的选取提供理论参考。