基于等效阻抗模型的应答器下行链路传输性能评估方法研究

李正交，蔡伯根,2，刘 江,2，陆德彪,2，朱林富，刘 浩

(1.北京交通大学 电子信息工程学院，北京 100044；2.北京市电磁兼容与卫星导航工程技术研究中心，北京 100044；3.中国铁道科学研究院集团有限公司 标准计量研究所，北京 100081； 4.北京交大思诺科技有限公司，北京 102206)

随着中国轨道交通近十年的飞速发展，应答器传输系统(Balise Transmission System, BTS)被大量应用于中国铁路列车运行控制系统(Chinese Train Control System, CTCS)[1]，以郑万高铁湖北段为例，全长287.187 km，需要采购和使用地面应答器近两千台。对2016年1月至2017年4月某动车段近200台列车的车载设备故障数据进行统计，发现应答器传输系统引起的列车车载系统故障占比近30%[2]。目前，针对应答器传输系统的维护和检修大多采用基于静态数据的“定期修”模式和基于动态检测的“故障修”模式，很难满足系统对进一步提高信息传输可靠性和降低维护成本的需求。随着新一代人工智能技术的发展，依据系统运行状况进行检修的“状态修”智能维护模式正在成为轨道交通行业革新的发展趋势[3-4]。“状态修”智能维护即在系统动态运行过程中，对系统性能参数进行监测，及时发现系统性能异常状态或定量评价系统健康状态、预测系统的剩余寿命，并在此基础上给出最优维护方案，而实现智能维护的关键就是对系统性能状态进行监测与分析。

近年来，部分学者已经对应答器传输系统的性能评估方法展开了相应的研究。赵会兵等[5]给出了特定应答器传输模块(Balise Transmission Module, BTM)设备的动态特性可以用动态作用距离、动态作用时间、动态接收能力、动态处理能力等参数描述，且这些参数可以通过生成最弱应答器及最强应答器上行链路动态模拟信号、采集BTM输出信息及状态的方法进行测试；李正交等[6]将BTM 报文层不能正确译码的概率作为系统可靠性评估的指标，对应答器传输系统的可靠性进行定量评估；朱林富等[7]采用参数S表征应答器内部有多个独立天线间的耦合磁通量大小，并对上行链路发射天线和射频能量接收天线间的互感性能进行仿真分析；梁迪等[8]深入分析了车载天线与地面应答器之间能量和数据的传输过程,建立了应答器 I/O 特性、射频磁场分布、信号辐射模式等理论模型，给出了计算应答器作用距离的一般步骤；赵林海等[9]针对应答器下行链路信号传输过程进行分析，提出应答器感应电压幅值包络来表征电磁感应强度。上述文献主要针对BTS车载模块或上行链路信号的传输特性进行监测和分析，而针对BTS下行链路传输过程仅停留在传输过程建模层面，缺少性能的评估与分析。因此，本文将深入分析BTS下行链路传输过程，给出其等效阻抗模型，提出可供铁路现场监测和分析的BTS下行链路传输性能评估指标，为应答器传输系统开展基于“状态修”的智能维护模式提供更多的性能评估思路。

1 下行链路传输过程分析

1.1 应答器传输性能的分析

应答器传输系统是一种基于射频识别技术RFID的点式列车定位系统，只有在列车通过地面应答器时应答器传输系统才能实现定位信息的无线传输。应答器传输系统功能示意见图1。

图1 应答器传输系统功能示意

列车运行过程中，应答器传输系统的下行链路信号和上行链路信号的传输极易受运行条件、环境等因素影响，其传输性能将不可避免地发生变化[5-7, 10-11]。应答器传输系统性能的变化可以看作系统性能退化的表现，严重的性能退化可能会导致系统最终的失效，进而影响列车运行控制系统的安全、高效运行。

为实现对应答器传输系统性能变化的监测和分析，本文以高速综合检测列车应答器传输系统动态检测为应用背景，假设监测过程中应答器传输模块及车载天线性能恒定不变；根据应答器传输系统铁路现场应用情况，地面应答器自身故障多为数据错误或硬件故障，数据错误多出现在新线路安装调试期间，而硬件故障常见于自身受外力击打损坏，如施工损伤、冰雪击打、应答器尾缆断线等[12]，因此在高速综合检测列车对应答器传输系统进行周期性动态检测时，可假设地面应答器自身性能也恒定不变。根据上述假设，本文重点对列车运行条件及环境引起的应答器传输系统性能变化过程进行评估。

列车运行条件及环境主要通过影响应答器传输系统“A”接口性能进而引起系统性能退化[6-7, 10-11]，为分析应答器传输系统的性能变化过程，需要对系统“A”接口信号传输过程进行建模分析。应答器传输系统“A”接口主要包括“A4”接口下行链路信号和“A1”接口上行链路信号，而上行链路信号的传输不仅受列车运行条件及环境的影响，而且受下行链路信号本身特性的影响，为简化分析过程，本文主要对应答器传输系统下行链路信号传输过程进行建模分析。

1.2 下行链路传输性能分析

搭建应答器传输系统下行链路传输过程的简化模型见图2，以地面应答器中心为坐标原点O，建立三维直角坐标系O-XYZ，分别取与地面应答器接收天线的EF边和EH边相平行的方向作为OX轴、OY轴，取与地面应答器接收天线垂直向上的方向为OZ轴，其中OX轴正方向为列车运行方向。车载天线水平安装，距地面应答器接收天线垂直高度h保持不变。

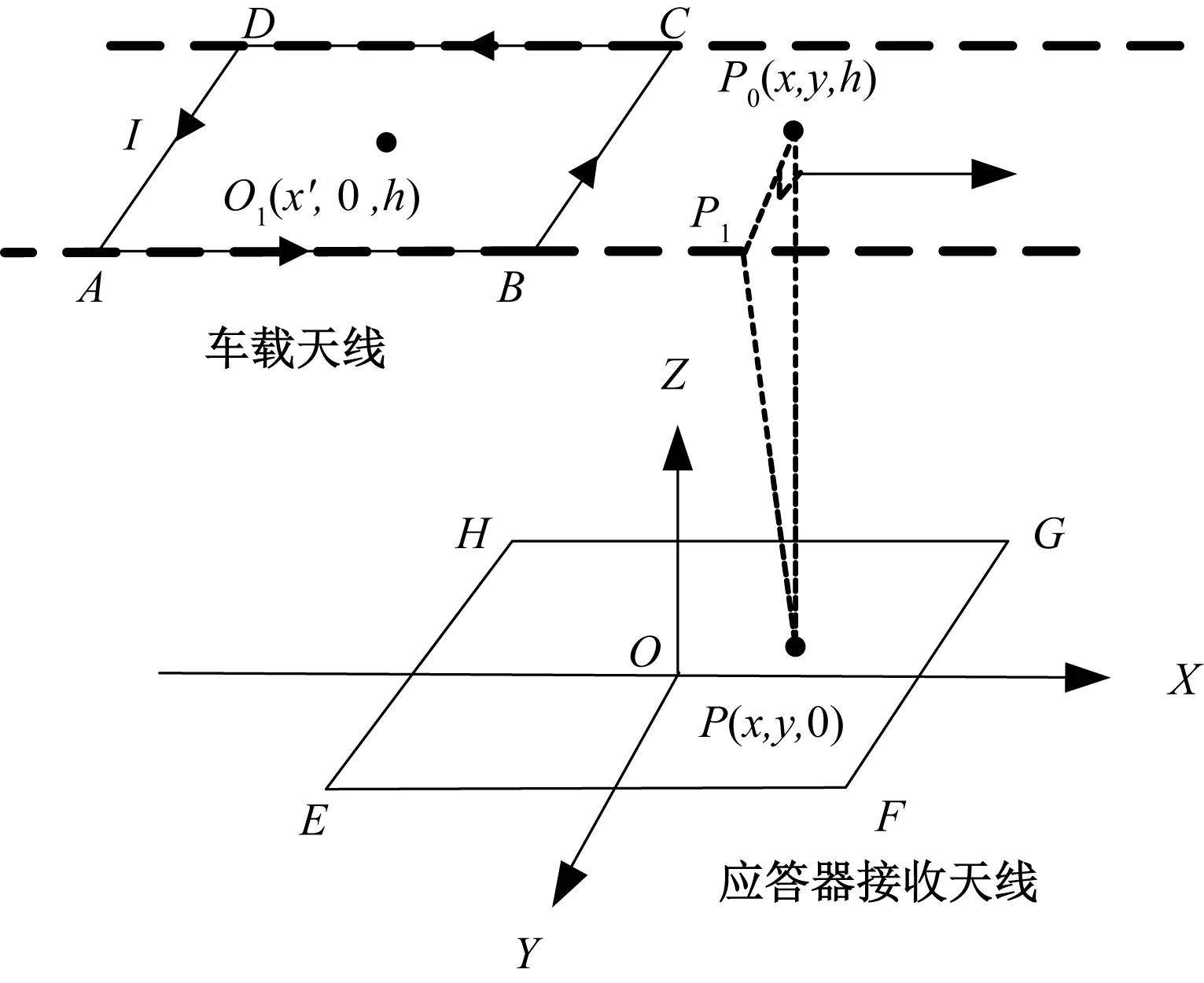
图2 BTS下行链路传输过程简化模型

设P0(x,y,h)为点P(x,y,0)在平面ABCD上的投影，P1为P0至AB边的垂足。车载天线的尺寸为AB=CD=2la、BC=DA=2lb，地面应答器接收天线的尺寸为EF=GH=2lc、FG=HE=2ld，车载天线中心点O1的坐标为(x′,0,h)。设t=0时刻，列车运行速度为v，车载天线中心点的水平位置为x0，则

x′=vt+x0

( 1 )

设μ0为真空磁导率，I为通过车载天线的电流，点Q1(xq1,yq1)、Q2(xq2,yq2)、Q3(xq3,yq3)、Q4(xq4,yq4)分别为AB边、CD边、BC边、AD边上的任意点。则由毕奥·萨伐尔定律分别计算AB、BC、CD、DA四个边在任意点P(x,y,0)的磁感应强度的Z轴分量BZ(x,y)的数学模型为[9]

( 2 )

在自由空间中不考虑环境因素的情况下，根据法拉第电磁感应定律知，地面应答器接收天线动态感应电压Uev(x′)的数学表达式为

( 3 )

式中：f0=27.095 MHz；q为地面应答器接收天线谐振电路的品质因数，负号表示感应电动势的方向总是阻碍磁通量的变化(楞次定律)。

根据式( 1 )～式( 3 )可知，当BTM性能及车载天线参数、地面应答器性能参数恒定不变时，地面应答器接收天线动态感应电压与下行链路信号磁感应强度是衡量BTS下行链路传输性能的两个重要参数[9, 13]，然而铁路现场不易或不可能对上述两个参数进行直接监测和分析，因而无法直接评估BTS下行链路传输性能的变化，因此本文提出了基于等效阻抗模型的方法对BTS下行链路传输性能进行评估。

2 下行链路传输性能评估方法

2.1 下行链路等效阻抗模型

为研究应答器传输系统下行链路传输性能与系统阻抗的关系，根据应答器传输系统车载天线与地面应答器接收天线的电磁感应耦合原理，应答器传输系统下行链路信号传输过程可以看作互感系数为M的互感电路，其等效阻抗模型见图3[10, 13-15]。

图3 下行链路传输过程等效阻抗模型

根据基尔霍夫电压定律知，当车载天线经过地面应答器时，下行链路信号传输过程等效电路满足

( 4 )

Ur=(Rr+jωLr)I0+jωMI1

( 5 )

式中:Up为车载天线的总电压;Ur为车载天线等效电路中端子1与端子2间的电压;ω为车载天线输入信号角频率;R1、C1为车载天线匹配电阻和电容;Rr、Lr为车载天线本身的固有电阻和电感;I0、I1分别为流经车载天线和地面应答器射频能量接收天线的电流。理想情况下，当车载天线阻抗与输入信号阻抗匹配时，车载天线输出功率最大，即回路处于纯阻性状态，满足

( 6 )

根据基尔霍夫电压定律知，当车载天线经过地面应答器时，地面应答器等效电路满足

jωMI0+(Rt+jωLt)I1+ZtI1=0

( 7 )

式中:Zt为地面应答器等效电路中端子3与端子4间的等效阻抗，包括阻抗匹配电路、整流电路和负载阻抗Zld；Rt、Lt为地面应答器射频能量接收天线本身的固有电阻和电感。

根据定义可知，车载天线输入阻抗Z0表达式为

( 8 )

将式( 4 )～式( 7 )代入式( 8 )得

( 9 )

由上式可知，地面应答器通过互感来影响车载天线输入阻抗[14]，可以用反映阻抗ZR表示为

(10)

根据互感系数M的定义知

(11)

式中：S为地面应答器下行链路信号接收天线所围成的面积。

由式( 9 )可知，当BTM性能及车载天线参数、地面应答器性能参数恒定不变时，应答器传输系统车载天线的输入阻抗Z0仅与互感系数M相关。而Z0可以被实时测量[16]，因此可以通过测量Z0来实现对BTS下行链路传输性能的评估。

2.2 等效阻抗的测量与校正

根据RFID系统实时阻抗测量方法以及地面应答器阻抗测量方法[14, 16]，可在列车通过地面应答器时，测量车载天线输入端S11参数，再通过误差校正方式来计算等效阻抗模型中车载天线输入阻抗。

车载天线输入阻抗Z0为

(12)

其中，S11参数定义如下

(13)

式中：b1为车载天线输入端的反射波；a1为车载天线输入端的入射波。

由于测量环境很难达到严格的电磁屏蔽标准，导致在测量过程中引入各种不必要的误差，进而导致系统测量得到的反射系数(ΓM)与真实的反射系数(S11并不相等。测量误差可分为漂移误差、随机误差和系统误差，而系统误差主要来源于定向器件的方向性、源和负载匹配、传输和反射跟踪，系统误差可以通过校准消除[17]。本文基于六参数双端口网络S参数系统误差模型，建立车载天线单端口系统误差模型[16-17]，见图4。

图4 车载天线单端口系统误差模型

图4中有三种系统误差：e00为方向性误差、e11为源匹配误差、e01、e10分别为入射端和反射端的频率响应反射跟踪误差。

通过图4可知，系统测量得到的反射系数ΓM与三种系统误差和车载天线真实反射系数Γc间存在一定的数学关系，根据梅森增益公式分析单端口系统误差模型可知

(14)

式中：S11M为S11测量值；Δ为信号流图的特征式；n为从源节点至汇节点前向通道总数；Tk为第k条前向通路的传输；Δk为第k条前向通路特征式的余因子式。Δe为

Δe=e00e11-e10e01

(15)

根据式(14)可知，车载天线真实反射系数Γc可以表示为

(16)

式中：Ar、φr为反射波的幅值和相位；Ai、φi为入射波的幅值和相位。

为计算e00、e11和Δe三个未知数，可分别测量开路、短路、50 Ω匹配负载三种典型负载情况下车载天线的反射系数ΓM1、ΓM2和ΓM3，得到方程组如下

(17)

其中，Γ1=ΓOPEN=1，Γ2=ΓSHORT=-1，Γ3=Γ50Ω=0。

根据e00、e11和Δe的求解结果，结合式(16)即可计算系统误差校准后车载天线输入阻抗的真实测量值。

由于铁路现场无法使用三种典型负载直接对BTS车载天线输入端口进行系统误差校准，可以参考地面应答器阻抗测量过程中的误差校准方法[14]，使用一个与地面应答器具有相同特性且负载可变的参考环来辅助校准，待系统误差校准完成后，将参考环替换成地面应答器再进行阻抗测量，而此时测量得到的阻抗是地面应答器的阻抗即反映阻抗ZR_Meas，因此车载天线输入阻抗的校正结果Z0_Eval为阻抗测量结果加上车载天线阻抗和参考环阻抗，其表达式如下

Z0_Eval=ZR_Meas+ZAnt+Zloop

(18)

式中：ZAnt车载天线阻抗；Zloop为参考环阻抗。

3 测量验证与仿真分析

3.1 传输性能评估方法验证

为了验证基于等效阻抗模型的应答器下行链路传输性能评估方法的准确性和可行性，参考UNISIG SUBSET-085规范[14]中地面应答器阻抗测量系统，使用示波器代替网络分析仪搭建一套车载天线输入阻抗测量系统，测量系统见图5。

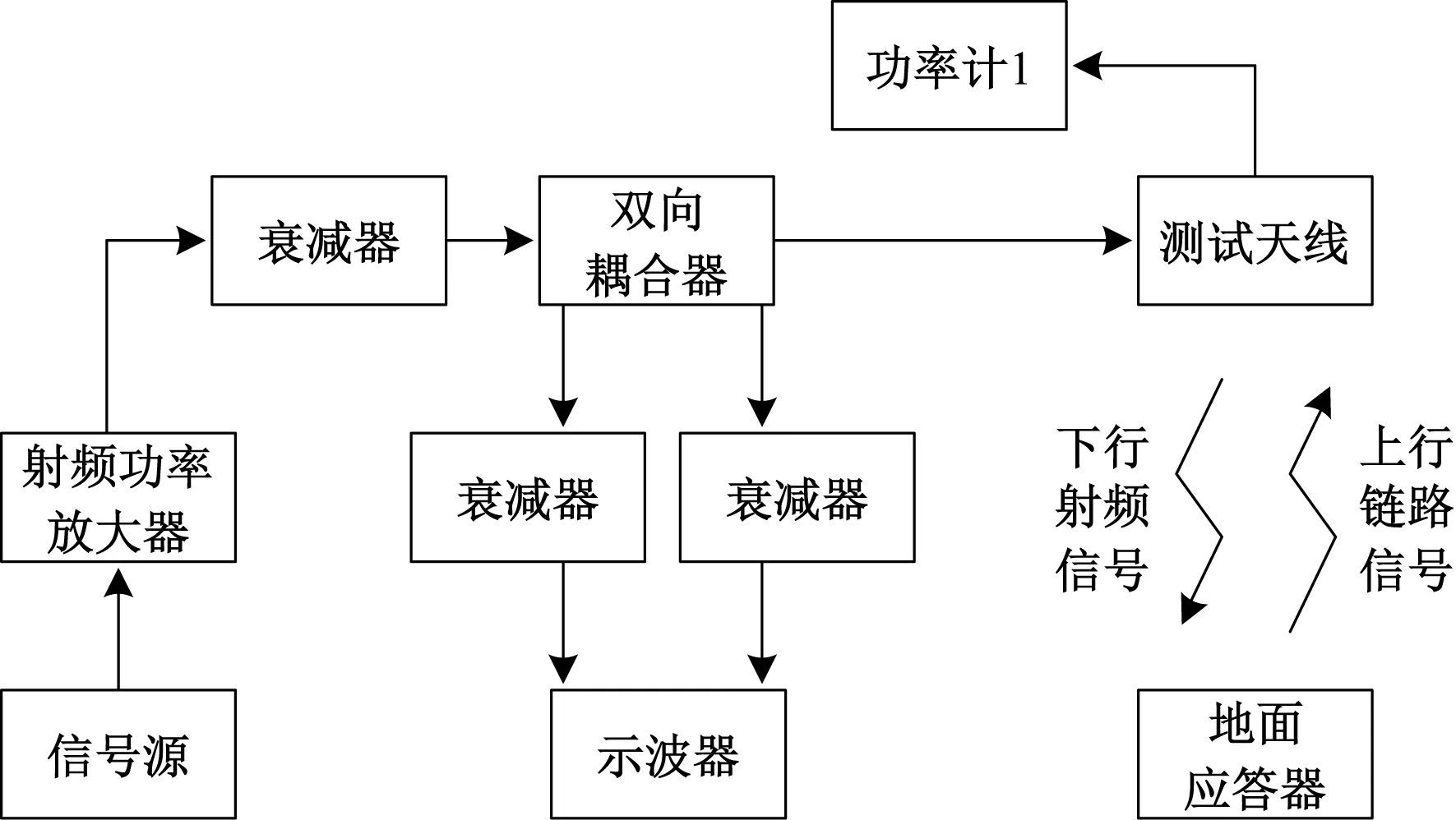
图5 车载天线输入阻抗测量系统

图5中，信号发生器产生27.095 MHz的下行链路能量信号，车载天线采用UNISIG SUBSET-085规范中专用的测试天线，通过示波器和双向耦合器对车载天线输入端的入射波和反射波进行测量，使用功率计对测试天线发射功率进行测量。

静态测试：选取某公司缩小尺寸地面应答器进行静态输入阻抗测试。车载天线相对于地面应答器的位置坐标为[X=0,Y=0,Z=220 mm]，在测量过程中两者相对位置保持不变，信号源发送固定幅度信号，通过调整射频功率放大器的放大倍数，不断改变车载天线发送功率。新方法与UNISIG SUBSET-085规范[14]中的测量方法对比结果如表1所示。

表1 新方法与UNISIG SUBSEF-085测量方法结果对比

表1中，阻抗模误差|Zerror|与阻抗角误差argZerror计算公式为

(19)

(20)

由表1可知，新方法所得的阻抗模误差、阻抗角误差均小于1%，新方法测量得到的车载天线输入阻抗能够满足性能分析对准确性的要求，而两者误差是由测量设备的漂移误差和随机误差无法消除且时刻变化引起，测量误差随着车载天线发送功率增大而减小，新测量方法将更加准确。静态测试时，车载天线发送功率与下行链路信号磁感应强度为增函数关系[14]，而根据表1的测量结果可知，当车载天线与地面应答器相对位置固定时，车载天线发送功率与输入阻抗的模之间也满足增函数关系，因此可以使用输入阻抗的模来间接分析下行链路信号的性能。

动态测试：选取某公司缩小尺寸地面应答器进行动态输入阻抗测试，由于铁路现场应答器动态检测时无法对每个测量点重新进行误差校正，因此仅对X=0处进行误差校正，在X≠0处仍采用X=0时的误差校正函数进行误差校正。车载天线相对于地面应答器的起始位置坐标为[X=0,Y=0,Z=220 mm]，在测量过程中信号源发送固定幅度信号，射频功率放大器的放大倍数保持不变，不断改变车载天线与地面应答器间的X轴的相对位置。动态测试结果见图6。

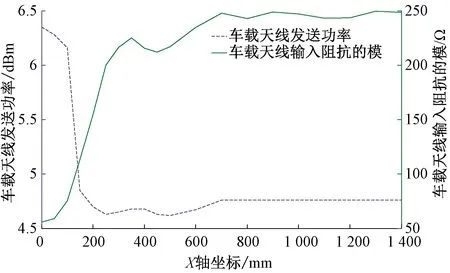
图6 车载天线输入阻抗的动态测试结果

由图6可知，在动态测试过程中，随着车载天线与地面应答器相对距离的增加，造成车载天线发送功率减小，进而引起下行链路信号磁感应强度减小，但动态测试结果显示，车载天线输入阻抗的模与车载天线发送功率满足减函数关系，此结果与静态测试结果正好相反，造成此结果的原因是动态测试并未对所有测量点进行单独误差校正，在X≠0处测量的输入阻抗，仍采用X=0处的误差校正函数进行误差校正，相当于将不同测试点测得的未经误差校正的输入阻抗按照X=0处的误差校正函数做了一次函数映射，从而得到图6的测试结果。动态测试更符合现场地面应答器的实际工作过程，上述结果表明，动态测量的车载天线输入阻抗的模可以间接分析下行链路信号的传输性能。

3.2 下行链路传输性能分析

在列车运行过程中，应答器传输系统的下行链路信号的传输性能极易受到运行条件、环境等因素的影响，可以通过变换车地相对位置、列车运行速度、空间环境介质等影响因素，来仿真分析车载天线输入阻抗的变化，由于仿真过程不存在测量误差，无需误差校正，因此车载天线发送功率与输入阻抗模之间会满足增函数关系。

假设应答器传输系统车载天线尺寸为la=187 mm、lb=218 mm，地面应答器接收天线尺寸为lc=100 mm、ld=195 mm，真空磁导率μ0=4π×10-7，车载天线电流I=0.48 A，下行链路信号频率f0=27.095 MHz，车载天线与地面应答器初始相对安装高度h=220 mm。且t=0时刻，车载天线中心点的水平位置x0=-1.3 m，仿真时长100 ms。

仿真实验1：改变车地的相对位置；假设列车以100 km/h的速度通过空间环境无杂质的地面应答器，以车载天线与地面应答器的相对位移X、相对高度h为变量，仿真在不同的车地相对位置下，车载天线输入阻抗的模见图7。

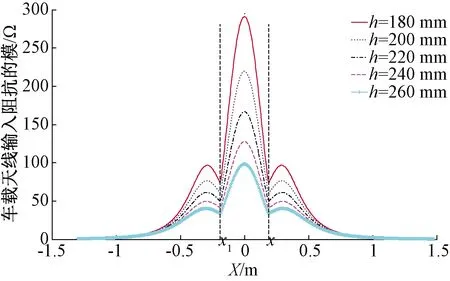
图7 |Z0_Eval|在不同车地相对位置的对比分析

图8 |Z0_Eval|在不同车地相对位置的特征对比

为定量分析不同车地相位置对车载天线输入阻抗模的影响，选取最大值、最小值、平均值、标准差、偏态、峰度共计六个参数作为特征值[18]，对图7主瓣区坐标X1至坐标X2间的数据进行统计分析，分析结果见图8。

仿真实验2：改变列车运行速度；假设列车分别以100、150、200、250、300、350、400、450、500 km/h的速度通过空间环境无杂质的地面应答器，车载天线与地面应答器相对安装高度h=220 mm，仿真在不同的列车运行速度下，车载天线输入阻抗模见图9，其主瓣区输入阻抗模的六项特征对比结果见图10。

图9 |Z0_Eval|在不同列车运行速度的对比分析

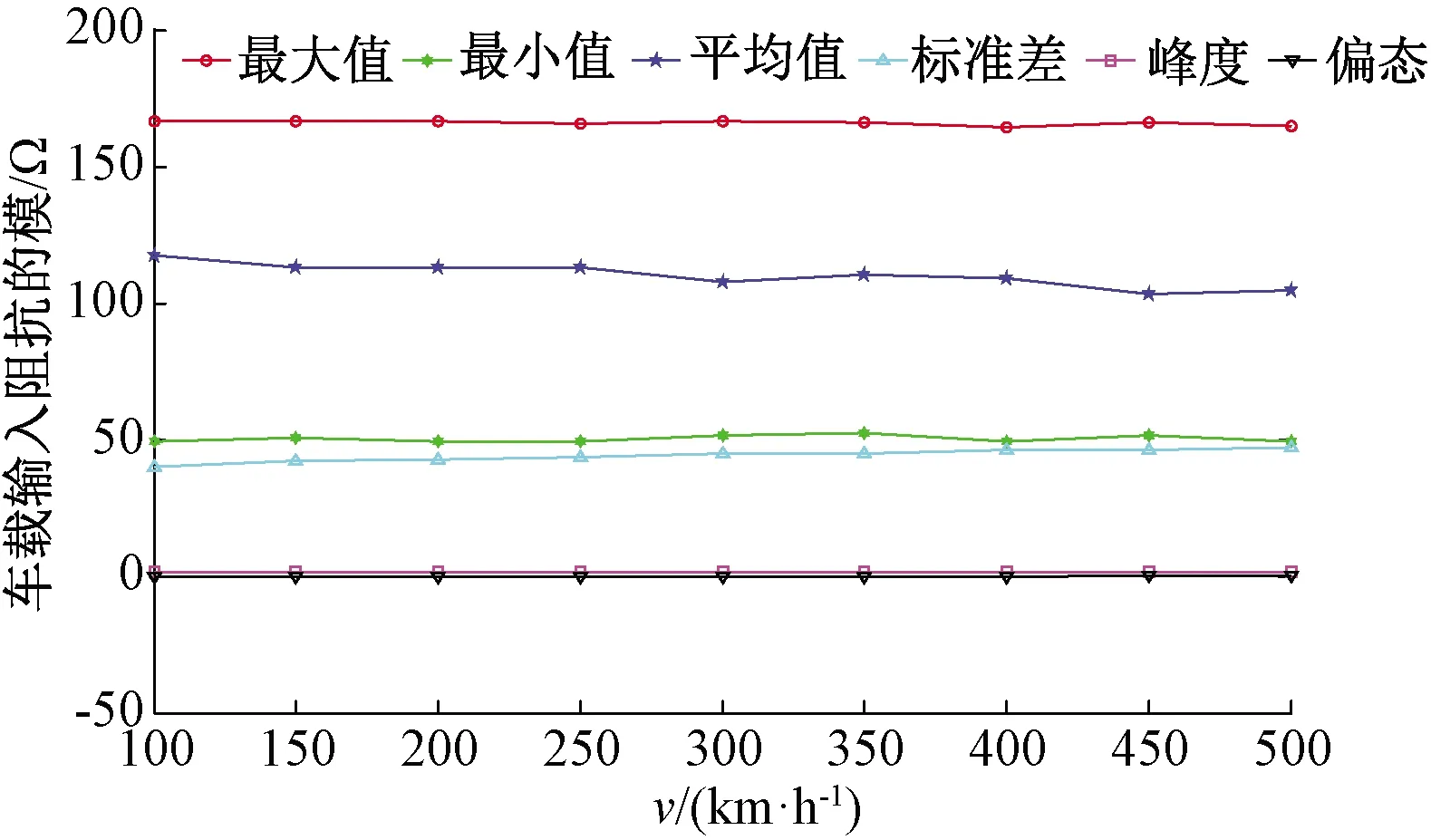
图10 |Z0_Eval|在不同列车运行速度的特征对比

图9中，X轴为仿真采样点数，Y轴为不同的列车运行速度，右侧Z轴代表车载天线输入阻抗模。

仿真实验3：改变空间环境介质；假设列车以100 km/h的速度通过表面有杂质的地面应答器，车载天线与地面应答器相对安装高度h=220 mm，仿真在损耗介质衰减因子α分别为0、0.05、0.1、0.5、1时[10]，车载天线输入阻抗模见图11，其主瓣区输入阻抗模的特征对比结果见图12。

图11 |Z0_Eval|在不同空间损耗介质的对比分析

图12 |Z0_Eval|在不同空间损耗介质的特征对比

根据上述三个仿真实验可以得出以下结论：①车载天线输入阻抗模的包络曲线与地面应答器接收天线接收到的磁通量包络曲线的变化趋势一致，可以表征下行链路传输性能的变化；②车地相对位置、空间环境介质的改变会引起车载天线输入阻抗模的包络曲线的变化，可通过对包络曲线主瓣区最大值、最小值、平均值、标准差等特征参数的分析，来实现对下行链路传输性能的评估；③列车运行速度的改变会引起车载天线输入阻抗模的包络曲线的变化，可以通过对包络曲线主瓣区采样点数等特征参数的分析，实现对下行链路传输性能的评估。

4 结束语

基于等效阻抗模型，提出一种适用于铁路现场监测与评估下行链路传输性能的新方法，引入车载天线输入阻抗模曲线主瓣区的六项特征参数，对不同列车运行条件和环境下车载天线输入阻抗模进行分析，验证车载天线输入阻抗对监测和评估下行链路传输性能的有效性。本文所提方法可以实现对应答器传输系统下行链路传输性能的监测和分析，但仅基于下行链路传输性能的状态还无法实现对应答器传输系统的在线智能维护，后续需要结合上行链路传输性能监测和分析结果，采用大数据与人工智能的方法，对应答器传输系统下行与上行传输性能进行综合监测与分析，来真正实现基于“状态修”的应答器传输系统健康管理。