基于二阶Keystone的空间目标检测方法*

陈睿容，孙武，贾学振，徐秋锋

(北京遥感设备研究所,北京 100854)

0 引言

微波主动探测雷达具备作用距离远、测量精度高、测量参数全、全天候工作等优势，在地基、空基等背景中，得到了大量应用。与地面的空间目标观测雷达相比，利用天基观测平台可以有效地降低大气传播抖动、电离层干扰等因素对信号的影响，对微小目标以及目标细节的观测有更好的效果，是未来发展的重点方向。但是，其体积大、质量大、功耗高等因素限制了天基轻小型化的应用,无法仅通过增大天线增益和提高雷达发射功率等手段提升探测威力[1]。

对回波信号采用长时间脉冲积累技术以提高检测前的信噪比，不需要大幅改进硬件设备的指标，利用信号处理方法就能够实现雷达对远距离低可探测性目标的有效检测和跟踪，且这种方法灵活多样，具有明显优势。由于雷达和目标通常处在相对运动的过程中，长时间积累时回波能量会分散在距离维和多普勒维的不同单元，传统的运动目标检测方法直接对回波做慢时间方向的快速傅里叶变换(fast Fourier transform，FFT)，只能积累同一距离和多普勒单元的信号能量。因此，如何解决信号长时间积累期间出现的走动扩散问题，实现目标回波能量的有效积累，成为小型化空间目标探测雷达探测弱目标的关键问题。

本文在雷达发射功率低，作用距离远，目标雷达散射截面积(radar cross section，RCS)小的情况下，分析了去斜脉压后的目标回波信号，针对长时间积累过程中各脉冲回波距离变化和多普勒扩散的问题，提出了一种小型化空间目标探测雷达检测弱目标的方法。首先通过二阶Keystone变换去除距离弯曲，然后用加速度匹配方法估计加速度以补偿二次项相位，接着再次运用二阶Keystone变换校正距离走动，最终实现弱目标的长时间脉冲积累和检测[2]。

1 双DDS雷达系统介绍

在对雷达信号进行脉冲压缩处理的过程中，传统的基于匹配滤波的脉压方式需要先对每个脉冲回波进行采样和数据存储，再通过匹配滤波实现脉冲压缩。为了满足奈奎斯特采样定理，这种方法需要的采样率比较高，采样后的样本存储量和脉冲压缩计算量非常庞大，由于实际工程应用中DSP运算速度和A/D采样器件水平的限制，难以满足现代雷达工程中宽带雷达信号处理的要求[3]。

基于双直接数字频率合成器(direct digital synthesis，DDS)架构的雷达系统能够有效解决上述问题。该系统在射频接收机接收过程中实现脉冲压缩信号的去斜处理，可以降低A/D采样速率，减少数据存储和运算量，从而降低系统硬件复杂度。针对空间目标探测雷达发射的线性调频脉冲信号，在射频组合中使用DDS2产生一个时间固定，载波频率、调频斜率与发射信号相同的线性调频信号作为参考信号，与目标回波信号做差频处理，使得目标回波信号与参考信号之间的时间差转换成不同频率的差频信号,实现回波信号的脉冲压缩处理。以相控阵体制雷达为例，系统组件和基本工作原理如图1所示。

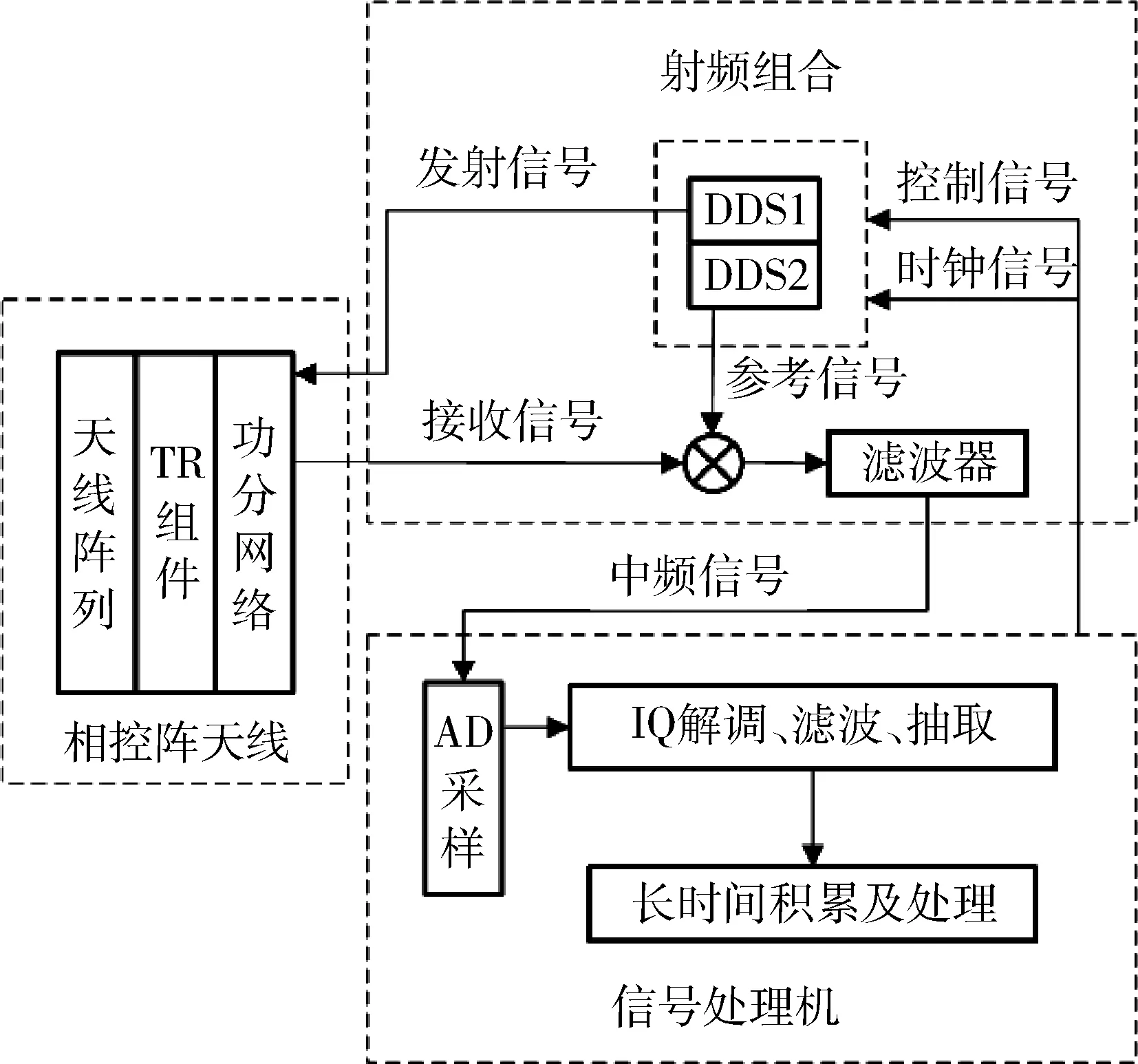
图1 小型化空间目标探测雷达系统Fig.1 Miniaturized radar system for space target detection

2 雷达目标回波模型与分析

雷达系统采用线性调频(linear frequency modulation，LFM)脉冲体制，发射载频为ej2πf0t，以Tr为脉冲周期重复发射，设在一个积累周期内雷达发射M个脉冲，每个脉冲的发射时刻记为tm=mTr(m=0,1,…,M-1)，称为慢时间。以发射时刻为起点的时间tk称为快时间，则发射信号表达式为

(1)

式中：Tp为脉冲宽度;f0为载波频率;t=tk+tm为全时间;γ=B/Tp为调频斜率，B为信号带宽。

在对目标进行探测捕捉的过程中，由于探测周期较短，可以认为加速度变化对目标运动带来的影响很小，将雷达飞行平台与运动点目标的相对运动近似为匀加速运动，设两者在初始时刻的距离、径向相对速度和径向相对加速度分别为R0,v0,a0，雷达和目标相互靠近时速度和加速度为正，相互远离时为负，则在第m个脉冲发射时刻，该点目标到雷达的瞬时距离为

(2)

雷达接收到该点目标信号为

(3)

式中：c为光速。

雷达信噪比计算公式为

(4)

式中：Pt为发射脉冲峰值功率；G为天线增益；λ=c/f0为信号波长；σ为雷达目标散射截面积(RCS)；M为相参积累脉冲数；k=1.38×10-23J/K为玻尔兹曼常数；T为开尔文温度；F为噪声系数；L为系统损耗[4]。

可以看出，当雷达发射功率越小，作用距离越远，目标RCS越小时，单个LFM脉冲的回波信噪比越低，目标的可探测性越差。为了让雷达既能满足小型化、低功耗的要求，又能实现对远距离弱目标的有效检测和跟踪，需要增加雷达回波的积累时间，提高检测信噪比。

DDS2产生的参考信号可表示为

(5)

式中：Rref为参考距离；Tref为参考信号脉宽。

用该参考信号与目标回波信号作混频处理，并去除差频回波的剩余视频相位(residual video phase，RVP)项和包络斜置项，最终得到回波差频信号表达式为[5-7]

(6)

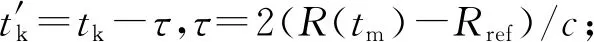
对式(6)作快时间域FFT可得

Sif(fr,tm)=ATPsinc(TP(fr+γτ))exp(-j2πf0τ).

(7)

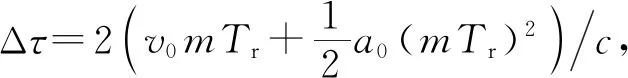
3 弱目标检测方法

3.1 弱目标检测算法总流程

针对空间弱目标长时间积累检测，本文提出了基于二阶Keystone的算法，首先对差频回波数据作二阶Keystone变换校正距离弯曲，然后通过估计加速度，补偿其引起的二次项相位，再作一次二阶Keystone变换完成距离走动的校正，最终通过慢时间FFT实现弱目标的长时间积累和检测[8]。算法总流程如图2所示。

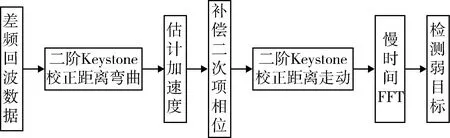
图2 弱目标检测算法流程图Fig.2 Algorithm flow chart of weak target detection

3.2 基于二阶Keystone变换的距离校正

而对于匀加速运动目标来说，由式(6)可知，各脉冲回波间不仅存在线性相位φ1，还存在二次相位φ2，从而引起距离走动和距离弯曲。要校正回波由慢时间变化引起的距离走动和弯曲，同样需要对慢时间作伸缩变换以去除回波中随脉冲数变化的相位因子。

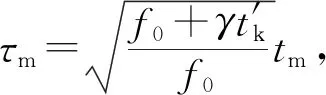
(8)

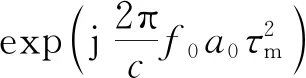
(9)

最终，各脉冲回波信号的包络都被校正都初始时刻距离处，相位则按各自的多普勒变化，这时对信号慢时间方向作FFT即可实现对目标的长时间相参积累，提高雷达目标检测信噪比。

3.3 二阶Keystone校正距离走动的实现方法

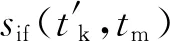
3.3.1 sinc函数内插法

由于雷达信号是以原来的慢时间tm作采样的，变换后的虚拟慢时间没有实际对应的采样值，因此，需要在原来的数据平面里插值得到Keystone变换后的信号采样点。

当信号最高频率有界且采样频率满足奈奎斯特采样率时，就可以从离散样本中无失真地重建初始信号。采样信号gd(i)的频谱是一个按采样频率重复的信号频谱，只需要理想矩形低通滤波器提取基带频谱，就可以实现信号g(x)的重建。该理想低通滤波器在时域表现为sinc函数，因此，可以通过将信号与sinc函数进行时域卷积来实现插值重建信号[14]：

③工程项目划分时，应按从大到小的顺序进行，这样有利于从宏观上进行项目评定的规划，不至于在分期实施过程中出现层次、级别和归类上的混乱，漏掉一些施工内容。一般在划分初期，首先对照初步设计批复文件确定单位工程，之后逐个确定分部工程、单元工程。质量评定时，由低层到高层逐级进行工程质量控制和质量检验。

(10)

sinc函数内插法实现二阶Keystone变换的公式为

(11)

3.3.2 变尺度变换法

(12)

(13)

由于FFT算法具有高效快速的优点，下面介绍一种改进算法Chirp-Z变换(简称为CZT)，将DFT表示成卷积形式，进而采用多次FFT实现DFT，将大大减小计算量，提高系统实时性能。CZT是采用螺线抽样，以各采样点的Z变换作为其DFT值，从而实现在非等间隔情况下求出各点采样值的快速算法。

一个N点长序列x(n)的Z变换为

(14)

沿Z平面的一段螺旋曲线作等分角抽样，抽样点记为

zk=AW-k=A0ejθ0(W0e-jφ0)-k,k=0,1,…,M-1，

式中：M为要分析的复频谱的点数；A0和θ0分别为起始抽样点的矢量半径长度和相角；W0和φ0则分别为螺旋伸展率和相邻抽样点之间的角度差。

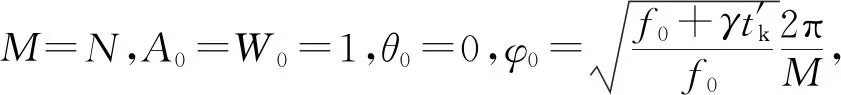
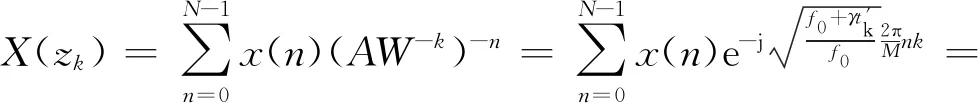
(15)

为实现二阶Keystone变换，取x(n)=s(l,m)，其中n与m对应。确定一个最小正整数L使其为2的整数次幂且满足L≥2M-1，其中M为一个积累周期的脉冲数。将g(n)和h(n)都扩充成L点序列并分别作L点FFT，有

(16)

(17)

G(k)=FFT[g(n)],

(18)

H(k)=FFT[h(n)].

(19)

由于时域卷积等于频域相乘，则有

(20)

此时得到的Z变换值等价于式(12)中的s(l,αk)，再作IFFT即可完成二阶Keystone变换[15]。

CZT-IFFT实现二阶Keystone的算法流程如图3所示。

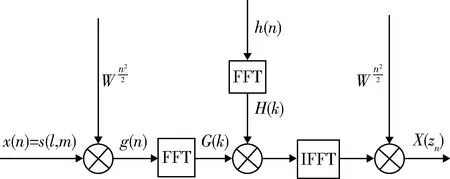
图3 CZT-IFFT算法流程图Fig.3 Algorithm flow chart of CZT-IFFT

3.4 基于加速度匹配的二次相位补偿

完成距离弯曲校正后的信号可以看作是一个对慢时间的线性调频信号，以Tr为脉冲发射周期，则信号离散形式可表示为

(21)

因此，通过估计该离散线性调频信号的调频率，即可构造一个函数H(τm)以补偿慢时间τm的二次项相位。

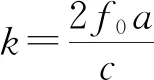
(22)

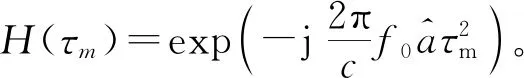
基于匹配方法的加速度估计算法流程如图4所示。

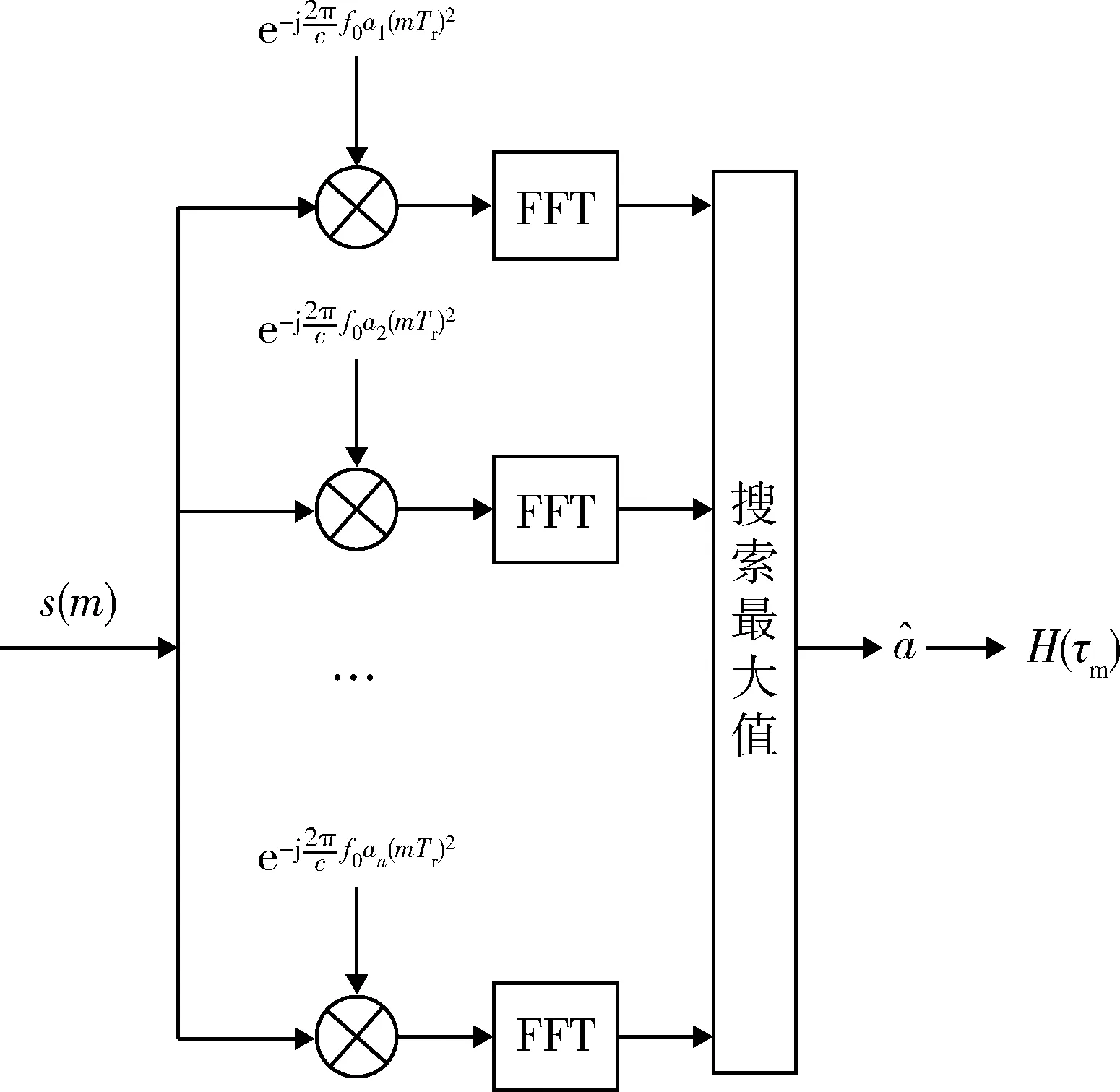
图4 加速度估计算法流程图Fig.4 Algorithm flow chart of acceleration estimation

4 相参积累时间捷变的快速搜索方法

如图5所示，由于接收机具有固定的带宽BF，得到的差频信号存在固定的频率范围，对于DDS2产生的某一参考信号，可测的距离范围也随之确定。因此，雷达系统通过控制DDS2产生不同延迟的参考信号可将探测区间划分为不同的距离段，从而可以根据系统要求的检测信噪比SNRt，在对不同距离段搜索目标时，自适应地确定所需的积累时间MTr，使其满足式(23)即可：

(23)

式中：Duty=TP/Tr为占空比;Rmax为当前距离段内的最大距离，目标RCS通常根据先验信息获得。

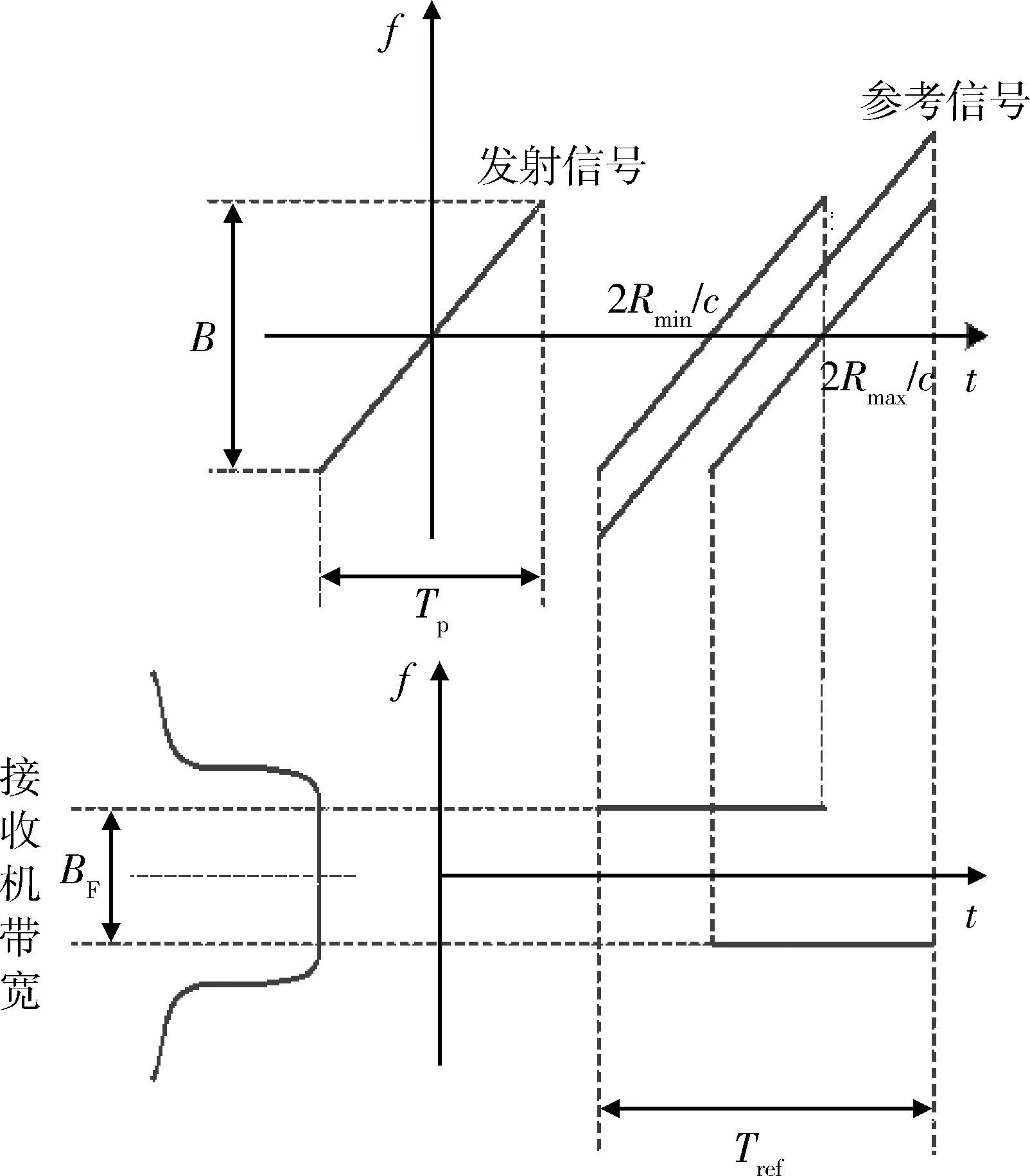
图5 去斜脉压时接收机带宽与测量距离范围关系Fig.5 Relationship between the receiver bandwidth and the range of measurement when dechirp pulse compressing

5 仿真校验

雷达系统仿真参数设置为：雷达发射功率1 W，天线增益33 dB，发射载频16 GHz。噪声系数3.5 dB，系统损耗4 dB。

5.1 弱目标检测仿真结果

为验证弱目标检测算法的有效性，设置目标参数为：目标与雷达平台的初始距离为20 km，径向相对速度为500 m/s，径向相对加速度为500 m/s2，目标RCS为1 m2。针对该目标所在的距离区间，设置雷达发射信号带宽为200 MHz，脉冲宽度为50 μs，雷达脉冲重复频率为5 kHz，以1 s为一个积累周期，积累脉冲数为5 000个，信号采样频率为50 MHz。

图6 无噪声状态下距离校正效果图Fig.6 Range correction effect in noiseless state

首先通过仿真验证本文算法对目标回波距离弯曲和走动的校正效果，如图6所示，图6a)，b)，c)分别为无噪声状态下距离校正前、去除距离弯曲后和校正距离走动后的结果。从图中可以看出，本文算法有效地校正了距离弯曲和走动。

接下来验证采用本文算法实现小型化空间目标探测雷达对弱目标回波的长时间积累的效果。在仿真验证的过程中在无噪声回波中加入高斯白噪声使得回波信噪比为-20 dB，以验证算法有效性。图7a)为信噪比为-20 dB的原始回波，图7b)为采用传统的运动目标检测方法时的积累效果，图7c)，d)为采用本文算法的长时间积累结果，分别

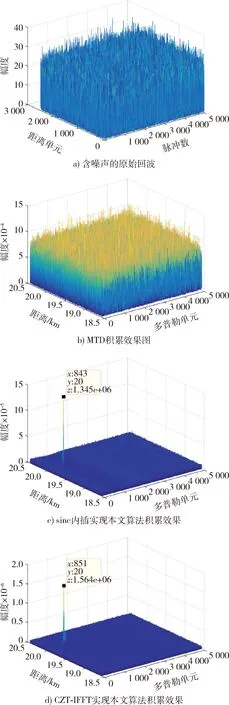
图7 SNR=-20 dB时仿真结果图Fig.7 Simulation results when SNR=-20 dB

用sinc内插法和CZT-IFFT法实现。

可以看出，对于运动的弱目标，采用传统的MTD方法后，目标信号淹没在噪声中，不能实现长时间积累检测，而采用本文算法，无论是通过sinc插值法还是通过CZT-IFFT法实现，都能利用长时间积累，获得积累增益约36.9 dB，从而有效地实现弱目标的检测。

5.2 二阶Keystone变换计算量分析

表1 Sinc内插法和CZT-IFFT法比较结果Table 1 Comparison of sinc interpolation and CZT-IFFT

可以看出，与sinc内插法相比，CZT-IFFT方法在有效提高信噪比的同时，算法运算量大幅减小，运算速度大大提高，因此采用CZT-IFFT法更有利于在工程实际中的应用。

5.3 快速搜索时积累时间与探测距离关系的仿真分析

为达到检测概率不小于0.99，虚警概率不大于10-8的要求，雷达检测所需信噪比为15.5 dB。目标RCS设为1 m2，雷达占空比设为0.25。此时雷达探测目标至少需要的积累时间与探测距离关系如图8所示。

部分距离对应需要的积累脉冲数和积累时间如表2所示。

本文对不同探测距离仿真时固定了雷达占空比，在实际工程应用中，可以根据不同距离分段设置脉冲重复频率和占空比，只需满足避免距离遮挡和距离模糊的要求即可。

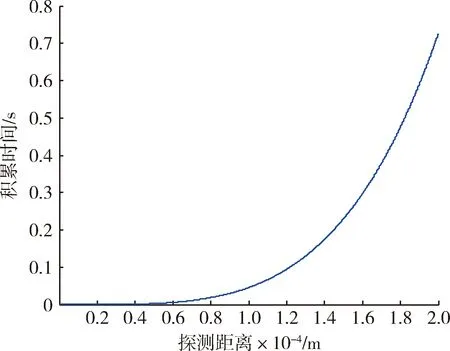
图8 信噪比检测门限SNRt=15.5 dB时积累时间与探测距离关系图Fig.8 Relation between accumulation time and detection distance when SNRt=15.5 dB

表2 不同距离对应的积累脉冲数和积累时间Table 2 Accumulation pulse numbers and time corresponding to different distances

6 结束语

本文提出了一种应用于小型化空间目标探测雷达的目标检测方法，分析了长时间脉冲积累情况下的远距离运动弱目标回波信号，采用二阶Keystone变换校正去斜脉压后目标回波的距离弯曲和距离走动，并用加速度匹配的方法估计加速度以补偿相位，最终实现弱目标的长时间积累和检测。针对不同探测距离段，选用不同的积累时间，使得目标搜索更加迅速。通过仿真分析，验证了本文方法的有效性，并比较了sinc内插和CZT-IFFT 2种二阶Keystone变换实现方法，CZT-IFFT方法在大大提高算法速度的同时，也能有效地实现算法功能。