导弹箱式垂直热发射过程燃气流冲击效应研究*
蓝仁恩,马艳丽,刘焕兴
(1.海装北京局第三代表室,北京 100081;2.北京特种机械研究所,北京 100143)
0 引言
发射箱可以为导弹提供较好的自然环境,对导弹起到保护作用,且在箱弹之间的适配器或某些弹性装置可以为导弹的初始弹道提供较好的动力学环境,因此,近年来,箱式导弹发射应用越来越广泛[1-2]。导弹箱式热发射过程产生的高温高速燃气流场在箱内受限空间排导,会对导弹及发射装置产生热力载荷,研究箱式导弹发射过程的热力载荷可以指导导弹和发射装置的设计。
Souraseni[3]对导弹倾斜热发射过程燃气流对导流器的热效应进行了计算。Nakai[4]等对倾斜发射燃气流场对平板的冲击效应进行了计算。Yoshinori[5]等对垂直发射过程燃气流对地面的冲击效应进行了计算。WANG Xi-kun[6]等采用计算流体力学方法对发射过程的超声速燃气流场进行了仿真,得到燃气流作用在发射装置上的力参数。York[7]等对导弹垂直热发射三维燃气流场进行了仿真研究,得到流场的参数分布以及作用在发射装置上的载荷。傅德彬[8]对导弹同心筒发射过程的燃气流场进行了数值仿真,得到燃气对同心筒的压力载荷并与试验进行了对比。姜毅[9]对同心筒发射过程的燃气流对发射装置的冲击进行了研究。马艳丽[10]等采用气固两相流对同心筒发射过程的燃气流对同心筒的冲击进行了研究。张英琦[11]等对同心同发射过程中收缩段对发射燃气流场的影响进行了计算。王学智[12]等对倾斜发射导弹燃气流场对发射箱前盖的冲击进行了数值模拟。从公开发表的文献来看,对导弹箱式垂直热发射过程的燃气流场的研究工作开展较少。
为了研究箱式导弹热发射过程燃气流场对导弹及发射装置的影响规律,采用计算流体力学方法,使用FLUENT软件,将多组分燃气流场和导弹运动耦合求解,采用域动分层动网格更新方法[13]模拟了导弹的发射过程,并与发射试验进行了验证。得到了箱式导弹发射过程中导弹及发射箱的热、力载荷分布规律,为导弹和发射装置的设计提供了依据。
1 方法
1.1 物理模型
1.1.1 计算模型
本文的计算模型由导弹、尾翼、发射箱和导流器等组成。图1所示为计算模型示意图。图2所示为计算区域网格划分。为了提高精度,整个计算区域采用完全结构化的网格划分。计算区域长50 m,宽5 m,高5 m,网格总数为500万。计算过程中分别对弹上和发射箱内壁面6个点进行压力和温度监测。图3所示为导弹及发射箱壁面观测点位置示意图。

图2 计算区域及网格划分Fig.2 Computational zone and mesh partition

图3 导弹及发射箱内壁面观测点示意图Fig.3 Scheme of the monitors at the missile and container inside surface
1.1.2 边界条件
喷管入口边界采用压力入口,总压在20 ms线性上升到6 MPa,总温为3 000 K。箱外燃气射流的边界条件为压力远场,环境压力为101 325 Pa,来流马赫数为0,温度为300 K。
1.1.3 壁面传热模型
导弹发射过程中,发射箱壁面和导弹壳体两侧为高温燃气射流或环境气流,需对壁面与流体的换热和壳体内部的热传导情况进行计算[14]。在本文研究中,使用对流换热方式处理壁面和高温燃气及环境气流的热量交换,使用热传导模型计算壳体内部的热量传递情况。图4所示为壳体壁面与流体之间的换热示意图。将壁面传热条件定义为对流传热,可以使用外部对流换热系数和外部气流的温度来计算通过壁面的热流率qf为
qf=hf(Tw-Tf),
(1)
式中:hf为外部对流换热系数;Tw为壁面温度;Tf为流体的当地温度。

图4 壳体壁面与流体之间的换热示意图Fig.4 Scheme of the thermal transfer between the wall and the fluid
壁面内部的固体区域也存在热量交换,由固体单元向壁面传递的热流率qs为
(2)
式中:ks为固体材料的导热系数;Ts为固体单元的当地温度;Δn为固体单元到壁面的距离。
1.2 计算方法
1.2.1 组分输运方程
燃气流是多组分的混合气体,总密度是各组分质量密度之和,总压力是各组分分压之和。
(3)
i组分的质量分数Yi和摩尔分数Xi分别为
(4)
多组分气体混合物及其各组分服从理想气体的状态关系,即
pi=ρiRT/Mi=niRT.
(5)
得到平均分子量M与各组分分子量Mi、质量分数Yi与摩尔分数Xi之间的关系为
M=∑XiMi,Xi=YiM/Mi.
(6)
多组分气体的定压比热Cp可以通过式(7)获得
(7)
多组分燃气流场中的3种宏观速度之间的关系式为
vir=vi-v
,
(8)
式中:v为混合气体相对于静止坐标系的速度;vi为i组分相对于静止坐标系的速度;vir为i组分相对于混合气体的运动速度。
与上述3种线性速度相对应的有3种物质流。ρv=g是混合气体总物质流;ρivi=gi是i组分物质流;ρivir=Ji是i组分扩散流。
i组分相对于静止坐标系运动的物质流等于该组分相对于混合气体的扩散物质流加上混合气体所携带的该组分物质流
gi=ρivi=Ji+Yiρv=ρivir+ρiv,
(9)
同时混合物物质流是各组分物质流之和。
g=ρv=∑gi=∑ρivi=
∑ρiVi+v∑ρi=∑ρivir+ρv,
(10)
因此可以得到
∑ρivir=0.
(11)
在多组分流场中,同时存在质量交换、动量交换和能量交换过程。另外,由于流场中有浓度梯度、速度梯度和温度梯度,因而产生质量交换的扩散现象、动量交换的摩擦现象和能量交换的传热现象。这些物理量的关系表示为费克扩散定律、牛顿粘性定律和傅里叶导热定律[15]。
1.2.2 导弹运动方程
导弹发射过程中沿发射箱轴向运动,轴线方向上受到发动机动推力、弹头空气压强阻力、弹底所受作用力、重力和摩擦力等5个力[16-17]。导弹加速度根据牛顿第二定律由导弹受力进行计算,合外力公式可采用
(12)
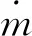
t时刻的导弹沿轴线方向的速度vt和位移lt分别由式(13),(14)求得,其中Δt为时间步长。
vt=vt-Δt+(F/M)Δt,
(13)
lt=lt-Δt+vt·Δt.
(14)
式(13)和式(14)给出导弹在任一时刻的运动速度,并由相应的运动边界更新网格,计算新网格下的流场参数分布,从而达到计算导弹运动过程中非定常流场的目的。
1.2.3 计算方法
采用有限体积法对燃气流场控制方程进行求解;采用一阶迎风格式对流场控制方程进行离散[18];使用基于密度算法的隐式求解器进行求解,湍流模型选用RNGk-ε模型[19],物面边界采用无滑移壁面边界条件,近壁面湍流计算采用标准壁面函数法处理。
2 结果与讨论
2.1 计算方法试验验证
在导弹发射试验中,对发射箱内壁面Pbox1和Pbox6在发射过程中的温度和压力进行了测试。图5所示为点Pbox1仿真与试验温度随时间变化对比曲线。由曲线可知,发射过程中,温度变化趋势基本一致,导弹在箱内运动过程中(0.14 s之前),箱内温度一直升高,导弹出箱后开始下降。
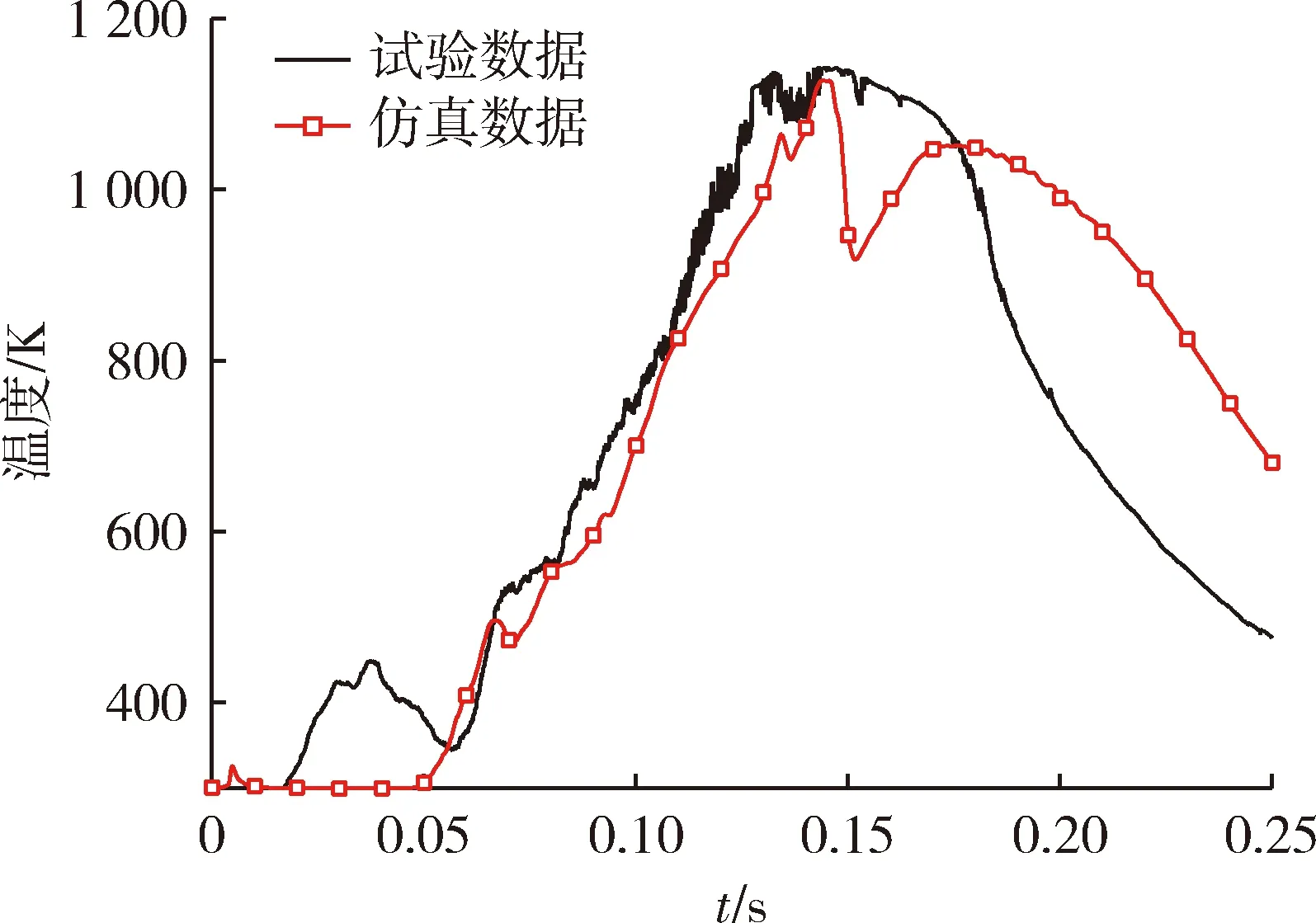
图5 Pbox1试验与仿真温度曲线对比Fig.5 Contrast of the experimental and simulative temperature of Pbox1
图6所示为点Pbox6仿真与试验压力随时间变化对比曲线。由曲线可知,压力趋势一致,试验测试压力振荡现象较仿真明显,导弹在箱内运动过程中由于负压作用箱内压力基本为负压,导弹出箱后,箱内压力上升。
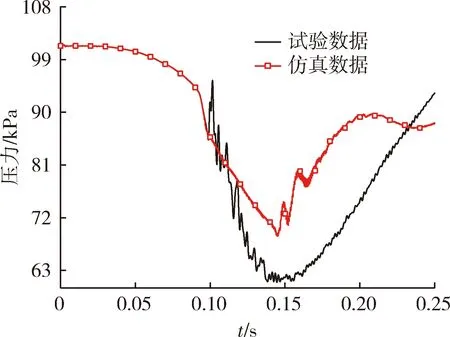
图6 Pbox6试验与仿真压力曲线对比Fig.6 Contrast of the experimental and simulative pressure of Pbox6
2.2 导弹热力载荷分析
图7所示为导弹壁面Procket1~Procket6点的温度随时间变化的曲线。由曲线可知,导弹底部的Procket1点的温度在0.001 5 s左右出现一个775 K的温度峰值,这是因为初始点火时刻燃气从喷管喷出,压缩空气,产生一个压缩波,作用在弹尾部,导致温度升高,之后温度迅速下降,到0.02 s时刻基本下降为300 K且一直保持变化较小。弹上其余观测点的温度在导弹整个运动过程中基本都保持在300 K左右,各观测点在导弹尾部出箱的过程中由于截面突变,产生扰动,温度会有较小的波动,之后恢复为300 K,燃气流基本无反喷。
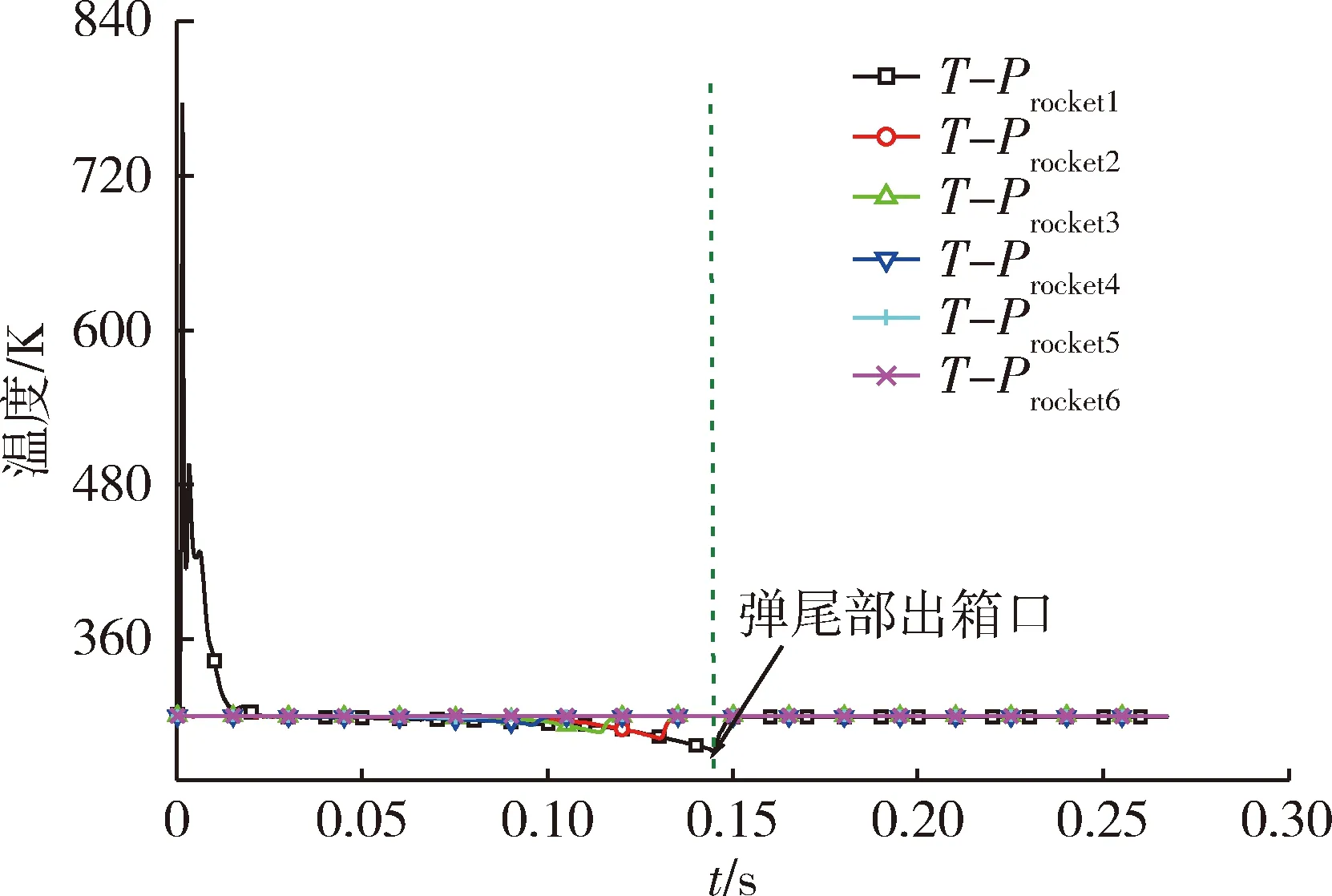
图7 弹上各监测点的温度随时间变化曲线Fig.7 Missile monitor temperature curve along with the time
图8所示为导弹壁面Procket1~Procket6的压力随时间的变化曲线。由曲线可知,点火瞬间,各观测点出现一个较小的压力峰值,最大为0.102 MPa,之后压力迅速下降,导弹在箱内运动过程中,弹表面的压力基本为负压,这主要是由于燃气流场的超声速流动引起的引射作用导致的,观测点越靠近弹底部,引射作用越明显,各点的引射作用随着导弹的运动而增强,Procket1点最低压力为0.066 MPa。弹体尾部约0.14 s左右出箱,各观测点导弹截面出箱以后,压力迅速升高,最高达到0.103 MPa,之后随着导弹原理发射箱,导弹表面的压力基本维持在一个大气压左右。
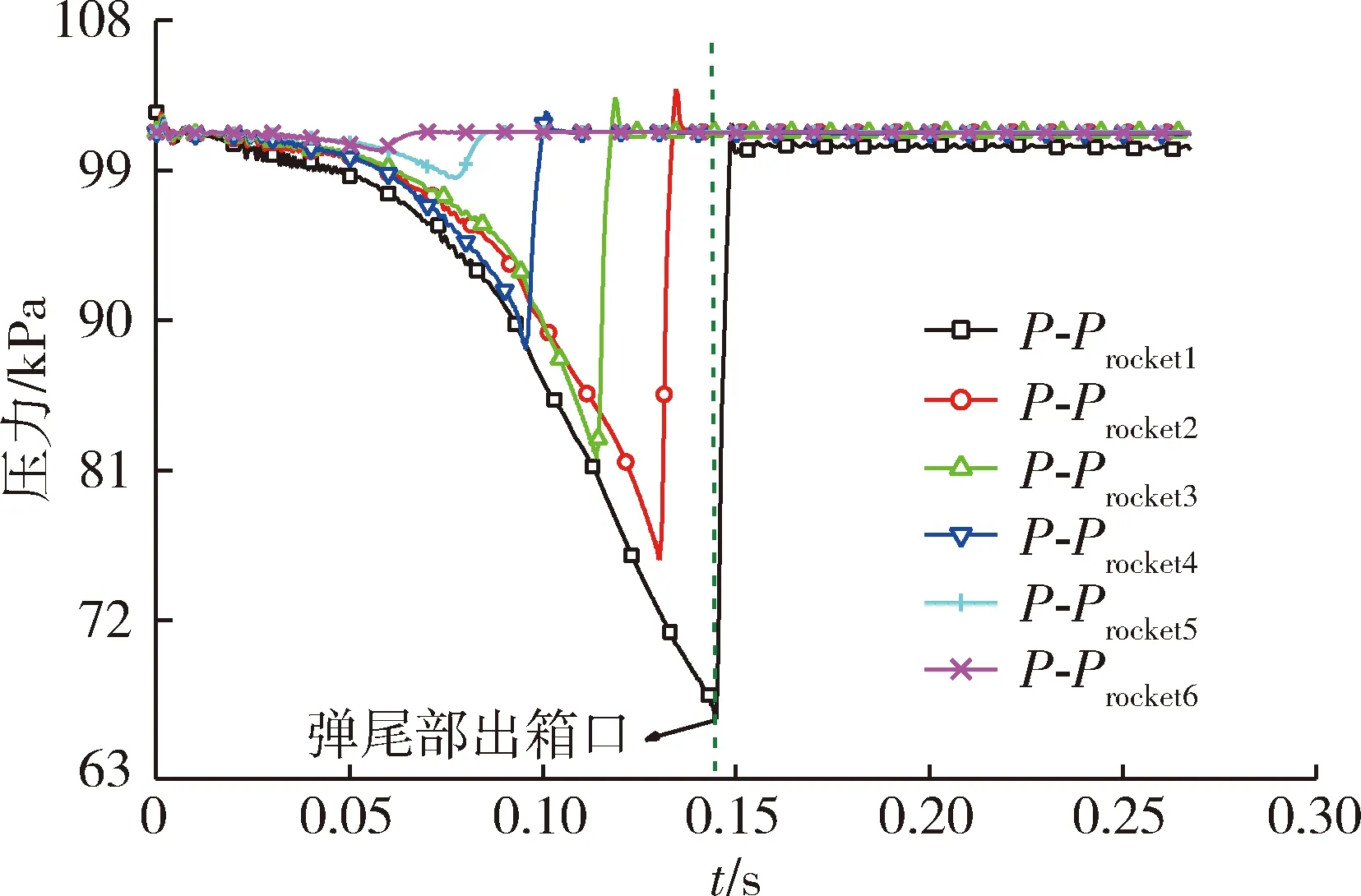
图8 弹上各点压力随时间变化的曲线Fig.8 Missile monitor pressure curve along with the time
图9所示为发射箱出口附近的流场迹线图。由图可知,箱口的流场速度为流向向内部方向,存在引射现象,会导致弹表面的负压。
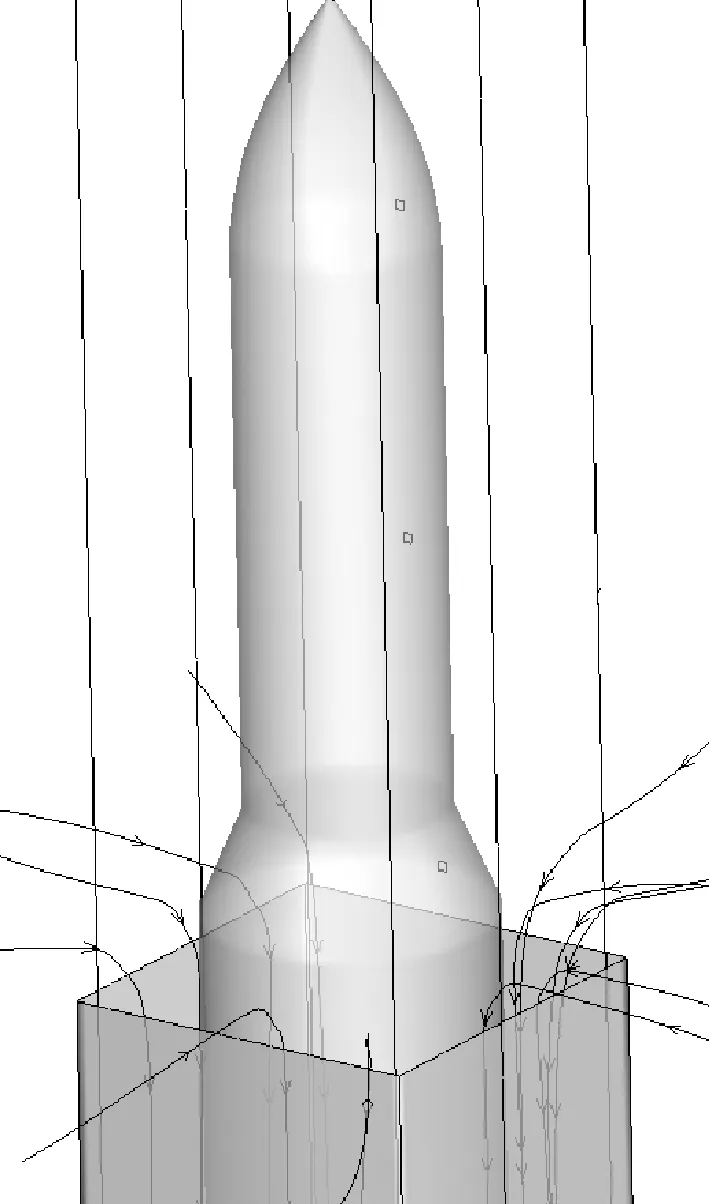
图9 发射箱出口附近的流场迹线Fig.9 Flowfield trace about the launching container exit
2.3 发射装置热力载荷分析
图10所示为发射箱壁面Pbox1~Pbox6的温度随时间变化的曲线。由曲线可知,箱内部的温度变化分4个阶段:第1阶段,导弹箱内运动,发射箱内壁面下部的4个点温度随着导弹运动而升高,温度升高越明显,弹底部的测点Procket1最高温度达到1 130 K,导弹尾部出箱时刻(0.14 s)发射箱内壁面温度达到最大值,而箱内上部的2个观测点Pbox5和Pbox6受引射作用较小,导弹在箱内运动时,Pbox5和Pbox6的温度基本为300 K;第2阶段,导弹箱外亚临界运动状态,0.14~0.15 s箱内温度下降,这是因为此时燃气流处于亚临界状态,燃气可以顺利从发射箱排导出去,因此温度降低;第3阶段,超临界运动状态,0.15~0.2 s,燃气流处于超临界状态,随着燃气流边界区的扩散,高温燃气无法顺利从发射箱排导,形成旁泄流,导致箱内壁面的温度升高;第4阶段,导弹远离发射箱状态,随着导弹继续运动,0.2 s之后,燃气射流对发射箱的影响越来越小,发射箱内壁面的温度逐渐降低。
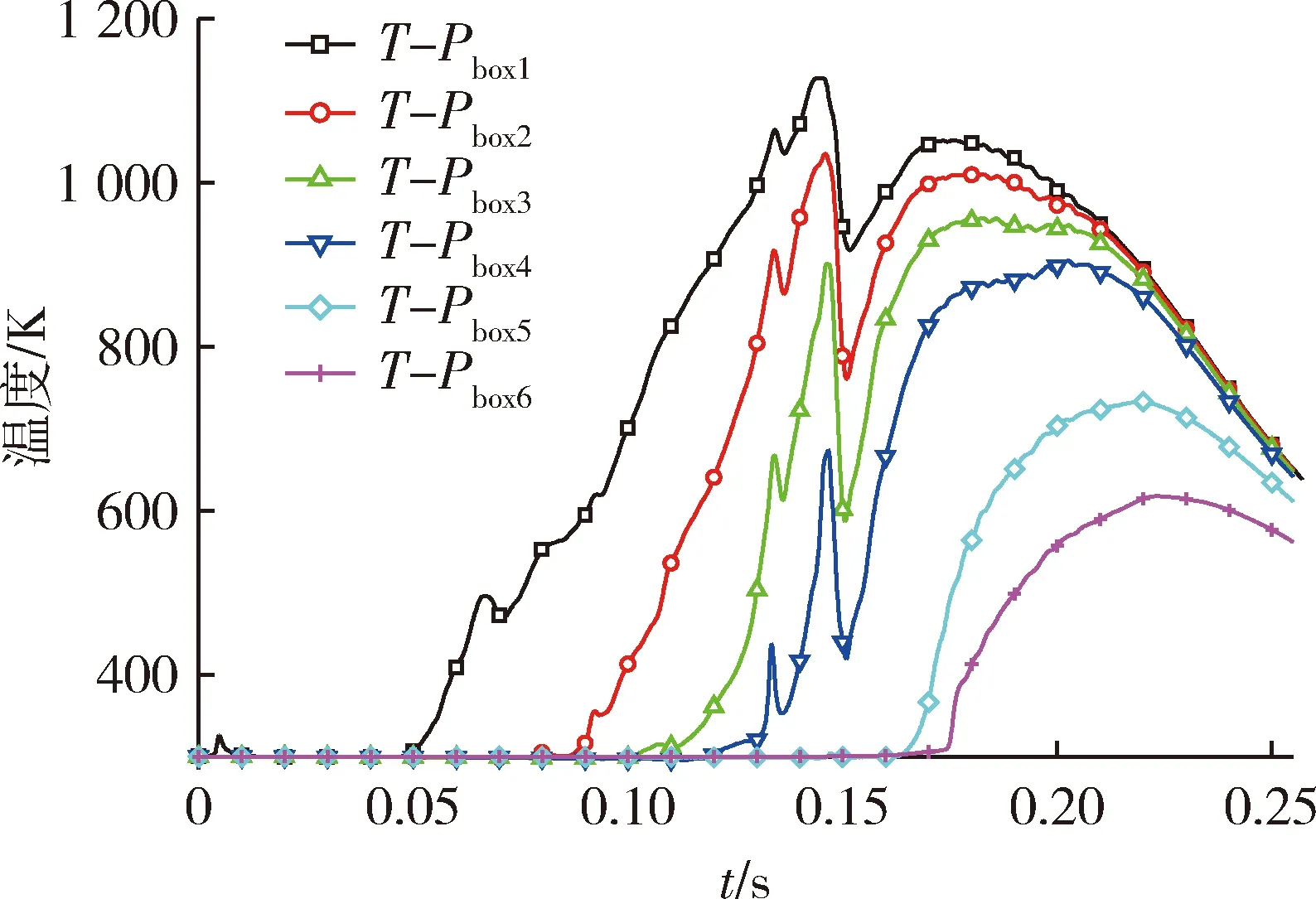
图10发射箱上点温度随时间变化曲线Fig.10 Container monitor temperature curve along with the time
图11所示为发射箱上的观测点Pbox1~Pbox6的压力随时间变化的曲线。由曲线可知,导弹发射过程中箱内由于燃气流的引射作用,基本为负压,导弹尾部的喷管运动到该观测点截面附近时,观测点压力降低到最小,这是因为喷管运动到该位置时,该处的燃气速度最大,导致引射作用明显,压力降低明显。喷管过了观测点以后,0.15 s之前,观测点的压力逐渐上升,0.15 s之后,燃气流由亚临界变为超临界状态,形成部分旁泄流,压力下降,形成一个波谷,随着导弹远离发射箱,发射箱内壁面温度逐渐升高为一个大气压。

图11 发射箱上点压力随时间变化曲线Fig.11 Container monitor pressure curve along with the time
2.4 发射过程流场分析
图12所示为导弹运动过程中典型时刻对称面的温度云图。由图可知,导弹发射过程中燃气流从喷管喷出,形成马赫波系,导弹出箱之前,燃气射流在发射箱发生壅塞,箱内温度升高,随着导弹的运动,尾部空间逐渐增大,燃气排导顺畅,箱内温度降低。随着导弹的继续运动,0.15 s之后,燃气流无法全部从发射箱排出,产生旁泄流,发射箱处于射流的边界区,发射箱温度有小幅升高,随着导弹逐渐远离发射箱,箱内温度降低。
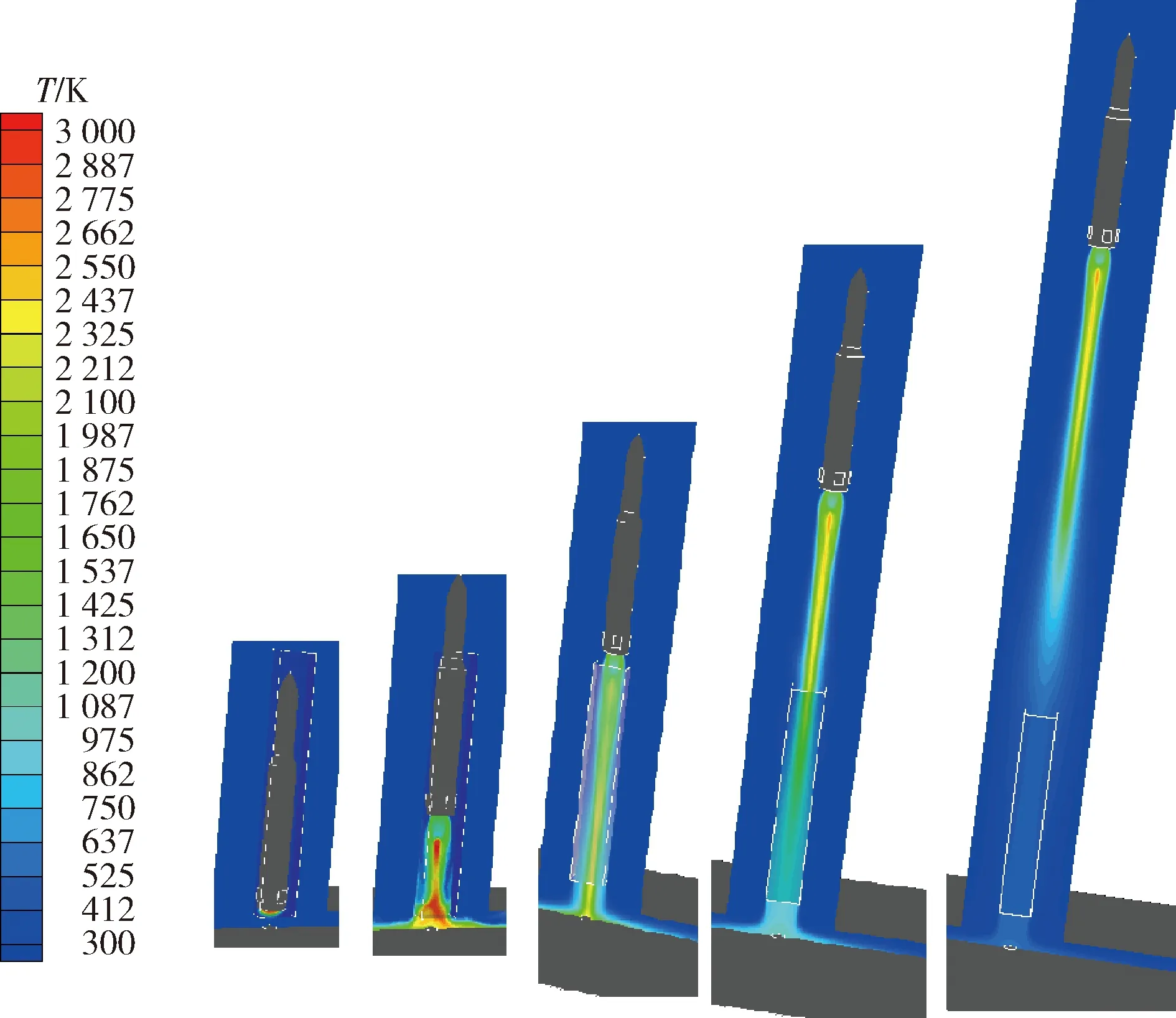
图12 导弹运动过程中对称面温度云图Fig.12 Symmetry temperature contour of the missile movement
图13所示为导弹运动过程中典型时刻对称面的速度云图。由图可知,0.1 s之前,喷管尾部的马赫盘在受限空间受到干扰,出现射流分离现象,高速射流冲击到导流器,速度滞止,并在导流器作用下产生贴壁射流。随着导弹的运动,喷管尾部空间增大,射流基本不受发射箱边界的影响。

图13 导弹运动过程中对称面速度云图Fig.13 Symmetry velocity contour of the missile movement
图14所示为导弹运动过程中典型时刻对称面的压力云图。由图可知,在射流核心区,由于膨胀波和压缩波的相交,在喷管尾部形成高低压场,在发射箱内部的上半部分,由于引射作用形成负压区。导弹出箱后,随着导弹的运动,箱内压力逐渐增大。

图14 导弹运动过程中对称面压力云图Fig.14 Symmetry pressure contour of the missile movement
3 结论
本文对导弹箱式垂直热发射过程燃气流冲击效应进行了研究,得到以下结论:
(1) 将监测点的压力和温度与发射试验进行了对比,结果趋势吻合较好,说明该方法可以用于计算导弹箱式垂直热发射过程燃气流场。
(2) 导弹在箱内运动过程中,受到燃气流引射作用,弹表面基本为负压,监测点越接近弹尾部,压力越低,Pbox1点压力最小为0.066 MPa,各测点导弹截面出箱以后,压力迅速升高为一个大气压,之后基本保持不变。
(3) 初始点火时刻,形成压缩波,会对弹尾部产生一个775 K的温度峰值,之后整个弹体表面的温度基本为300 K左右,各观测点在导弹尾部出箱的过程中由于截面突变,产生扰动,温度会有较小的波动,之后恢复为300 K。
(4) 箱式垂直导弹发射过程中,发射箱的温度变化分为4个阶段:第1阶段,导弹箱内运动阶段,箱内温度随着导弹运动而升高,最高达到1 130 K;第2阶段,导弹箱外亚临界运动状态,箱内温度下降;第3阶段,超临界运动状态,燃气流无法全部从发射箱排出,形成旁泄流,导致箱内壁面的温度升高;第4阶段,导弹远离发射箱状态,发射箱内壁面的温度逐渐降低。
(5) 箱式垂直导弹发射过程中,导弹发射过程中,箱内压力基本为负压,喷管运动至观测点截面附近时,观测点压力降至最低,之后压力缓慢升高,0.15 s之后,压力下降,形成一个波谷,随着导弹远离发射箱,发射箱内壁面压力逐渐升高为一个大气压。
(6) 箱式垂直导弹发射过程中,导弹表面基本为负压,导弹表面的温度在初始时刻有个峰值,之后一直处于常温状态;发射箱基本经历温度升高、降低、升高再降低等4个阶段,发射箱压力基本由负压慢慢增大至一个大气压。

