东河特大桥梁场条形基础承载力计算研究

蒋仁国 孙德金 武建林

【摘  要】在临建工程中，涉及到条形基础计算的很多，如地鐵上轨道梁基础、支架下面的扩大基础、梁场的台座基础等，都涉及到条形基础的计算。而且条形基础计算方式很多，不谈优劣，但到底哪种更适合现场需要，可以做进一步的探讨，总结更适合的方式。

引文：

本文通过现场几个临建方案中扩大基础的计算，对比几种计算方式的方便程度，以便后面采取更方便的方式进行扩大基础的验算。

一、临建中条形基础设计现状

目前在施工临建中，条形基础的使用范围广，无论是铁路、公路、市政工程等都能涉及的到。但查阅各种方案，形基础的计算方式多样化，基本上可以分为两大类，一类是按规范上的经验公式计算，另外一类是采用有限元类的进行模拟计算，这一类有的是采用梁单元底面加弹性约束实现，有的是采用实体单元，把条形基础和土体全部建模，利用相互之间接触面的应力来表示所需要的承载力。但无论采用哪一种，都有其优缺点。有的是计算偏保守，有的是计算偏繁琐，到底哪种更适用，我们分类列举一下。

二、条形基础计算实例分析

在成昆铁路峨米段东河村双线特大桥节段梁预制场的临建中，也涉及到了轨道梁基础及箱梁存放台座基础设计，这些都是条形基础。下面以轨道梁基础为例，来探索几种计算方法的区别与优劣。

1、轨道梁基础介绍

东河特大桥节段预制场中轨道基础采用C30混凝土条形基础，与地面平齐，宽1.6m，深0.5m，按160t吊重进行轨道基础检算。下面分别用经验公式法、有限元模拟梁单元法和实体单元法进行对比计算分析[1]。荷载情况龙门吊自重：100t;最大荷重：最大起吊物为2#梁段，重约160t;单腿分担荷载：160*21/24=140t，则单侧最不利荷载为100t/2+140t=190t。

1.1采用传统经验公式进行计算

单侧荷载平均分配给8个走行轮，则每支腿所承受的荷载为：190t/2=95t。考虑不均匀及冲击因素，每支腿所承受的最大荷载按95t×1.1=105t考虑，单个走行轮轮压为105t/4=26.125t。此处不考虑轨道刚度。

基础宽1.6m，轮组间距0.60m，地基处理采用50cm混凝土+50cm砖渣土，地基扩散角按30度角考虑，地基受力面积为（1.6+0.8×0.57×2）m×（3×0.6+2×0.50+0.8×0.57×2）m=2.512×3.712=9.32m2。

地基受到的附加应力为：P=105×104/9.32=113 Kpa，现场测得最小地基承载力为230KPa，满足要求。

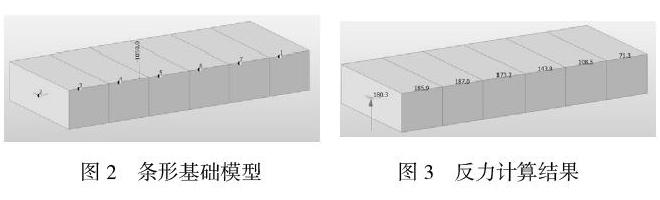
1.2 采用有限元梁单元法进行计算

在有限元中，为了更好的模拟基础与地面接触作用，同时为了更方便的得出需要的地基承载力，一般在划分梁单元时，与地面接触长度折合成面积正好是1m2时采用一个支座，这时支座所需要的反力正好时所需的地基承载力。在有限元计算处理中，类似等量代换的方法很多，在一定程度上简化了计算。因为基础宽为1.6m，折合成1m2长度就是0.625m。此时我们采用6个节段长既3.75m的梁长来进行计算。在有限元软件上我们采用midas civil进行模拟分析。

由结果可知，在距轮最近的两个节点的支撑反力最大，所需的地基承载力较大，最大达187KPa，现场地基虽能满足要求但是远比传统的手算需要的地基承载力大的多。实际轨道梁基础的长度远大于我们所取的计算长度，所以在施工中实际所需要的承载力要稍于小我们计算所需的承载力。

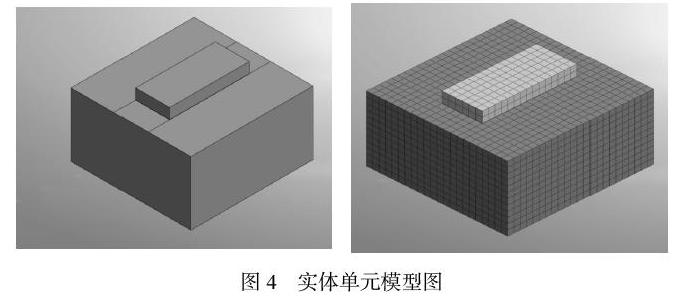
1.3 采用实体单元进行计算

若用midis GTS建立实体模型，取和杆系单元相同长度的来取值，下方设置一块土体。为了更好的模拟实际效果，土体比轨道梁在长宽方向上多出1m，建立实体模型。网格才用四面体或六面体混合网格。对混凝土和土体的材料性质进行定义，在中间加一集中荷载与上述荷载相同大小，来模拟龙门吊传来的荷载。假设土体底部为固定边界，用混凝土轨道梁和土体相互的接触面的Z向应力来表示土体所需的承载力，这样和现场的情况更加接近。

经过计算分析结果如下：

由此可见，无论是土体上表面还是轨道梁的下表面，竖向应力在200KPa左右，证明土体至少需要200KPa的承载力，才能满足承载力的要求[2]。

2、三种计算方式对比

2.1传统计算方法优劣

传统的计算方式计算结果所需要的承载力较小，因为在传统的计算方式上，没有考虑结构物如轨道梁本身的刚度，为了计算简便，是把轨道梁的刚度看作无限大来处理的。轨道梁上受力集中在一点上，由于假定在是轨道梁刚度无限大，则轨道梁内部不会产生变形，对于与之相接触的地基来说，接触面所需的承载力是平均的，这样计算出来的结果相对来说较小。而实际轨道梁由于受力比较集中，并不是平均受力，本身刚度有限，所以自身也会发生一些微小的变形。变形大的地方与土体接触的面受力较大，此处的土体所需的承载力就越大。这是传统计算方法与实际之间差距。但优点是传统的计算方法较简单，没有考虑条形基础具体的受力情况及变形特征，也没有涉及条形基础的材料的各种物理参数，如弹模、截面形状，计算相对片面，结果可能和实际相差较大，可能要考虑一定的系数，以便满足现场需要，这种算法只能在一定程度上做为施工时处理地基的参考。

2.2采用梁单元有限元模拟的优劣

采用有限元中梁单元，边界条件是有一定刚度的节点弹性支撑进行计算模拟，相对传统的计算方式，首先计算比较快捷，建模分析比手算要快的多。其次，把轨道梁基础做为有刚度的梁来考虑，梁体的各个参数都能在计算中体现出来，并且影响结果的分布。在模拟中能体现出来轮门吊轨道轮所处位置前后所需要的承载力，土体纵向上不同地方体现出需要不同的承载力，但毕竟是梁单元所限，梁单元有纵向刚度参数，没有横向刚度参数。在横向上土体所需要承载力的分布情况体现不出来。但是施工时这种模型基本上能满足需要，不用再去考虑折减参数，相对来说是比较理想的计算方式。

2.3采用实体单元有限元模拟的优劣

采用实体单元进行计算模拟，相对其它两种计算方式来说，建模过程比较复杂，有轨道梁的建模，也有对下面土体的建模，利用轨道梁与土体接触面的Z向应力来表示所需的承载力，和实际情况是一致的。而且土体的弹模、厚度等参数，轨道梁的截面及材料参数都参与了计算，虽划分网格，计算所需的资源较多，时间较长，但能比较真实的模拟现场的实际情况，而且结果显示较详细，从轨道轮接触点为参考点，相对这个点其它位置的力的分布情况能完整的呈现出来，而且和现场实际情况高度吻合，能用来指导现场确定现场方案。

三、上述条形基础载载力计算优化

以上通過三种计算，都能计算出了条形基础的地基所需的承载力。但详细程度与准确程各不相同。在计算中，实体单元模拟是最能接近实际的，也是最理想的结果。但在现场施工中，有时为了计算简便，可能采取了传统上的简单手算，由于计算参数较少，过且理想化，需要加上一定的安全系数满足施工需求。其余两种有限元法只要取其最大值基本满足现场的施工需要，为施工方案的确定提供参考。只不过实体单元的方法能体现出在轨道梁宽度范围内所需要的承载力的分布，而梁单元法只能在轨道梁长度上提供了最大所需要的承载力，有限元法在计算上比较便捷，但是结果受地基弹性系数的参数限制，所取参数不准，可能会出现较大的偏差。

四、设计行业条形基础承载力的计算

在建筑结构设计中，一般设计上部结构是把支座看成是刚性的固定支座，求得支座的反力。在设计基础时把反力作用于基础，用材料力学的方法求得地基反力后，再对基础的内力和变形进行计算，然后把基础的反力作用于地基，验算地承所需的承载力和沉降[3]。条形基础的计算又分常规的计算方法和弹性地基梁计算方法。在常规计算方法里，条形基础做为梁来进行计算，它的支座是有限的，支座的反力是未知的，刚度是无限大的，而实际条形基础与地基接触是连续的，支座是无穷多的，梁与地基是共同变形的，这样才能满足其变形协调的条件。常用的弹性地基梁法有倒梁法、弹性地基梁法如文克勒地基模型、另外还有有限元法。

总之，无论采用哪种方法，都要根据上面结构的重要程度及对变形的敏感程度来定，传统方法简单但精度差，需要一定的系数保障，有限元法快捷，但是受地基弹性系数的影响较大，弹性系数取值和实际偏差大而计算结果出入较大。现场还需要根据实际情况具体分析，选择合适的计算方法。

参考文献：

[1]杨军宏.《软弱土层上柱下条形基础的计算方法对比分析》[J]，施工技术. 2019，48（S1）

[2]刘正保，王晓睿.《砌体结构墙下基础设计的对称修正》[J]，山东建筑工程学院学报. 2005，（02）

[3]王士杰，张梅，张吉占.M indlin 应力解的应用理论研究【J】.工程力学，2001，l8（6）：141—148

作者简介：

蒋仁国，1974，10-，汉族，男，重庆人，研究生学历，高级工程师，专业方向：隧道施工;

孙德金，1979，8-，汉族，男，吉林农安县人，本科，高级工程师，专业方向：桥梁施工;

武建林，1982，9-，汉族，男，山东莘县人，本科学历，高级工程师，专业方向：路桥施工。