基于反应扩散方程研究新型冠状病毒肺炎在武汉早期传播特征
郭尊光, 李明涛, 常利利, 张 娟, 梁 娟, 邢国荣, 张 伟, 孙桂全3,,†
(1- 中北大学大数据学院,太原 030051; 2- 太原工业学院理学系,太原 030008;3- 中北大学理学院,太原 030051; 4- 太原理工大学数学学院,太原 030024;5- 山西大学复杂系统研究所,太原 030006;6- 疾病防控的数学技术与大数据分析山西省重点实验室,太原 030006)
1 引言
传染病自古以来就是危害人类健康的主要敌人之一,预防和控制传染病仍然是当今世界的重要课题.冠状病毒是一类具有包膜、基因组为线性单股正链的RNA 病毒,这种病毒会引起疾病,患者表现为从普通感冒到重度肺部感染等不同临床症状.根据武汉市卫健委通报的武汉肺炎情况,新型冠状病毒是一类β 属的冠状病毒,有包膜、呈圆形或椭圆形颗粒,直径60–140 nm.感染新型冠状病毒主要表现发热、干咳、乏力.潜伏期为1–14 天,多为一周左右.重症患者出现呼吸困难,严重者表现为急性呼吸窘迫综合征、脓毒症休克及多器官功能衰竭.新型冠状病毒肺炎已被纳入《中华人民共和国传染病防治法》规定的乙类传染病.为防止新型冠状病毒肺炎疫情传播和扩散,最大限度的保障人民群众的健康,为加强全国面上的疫情防控工作.先后有30 个省启动了突发公共卫生事件的一级响应.世卫组织总干事2020 年3 月13 日在2019 冠状病毒病(COVID-19)疫情媒体通报会上的讲话中提及,全球确诊病例已超过13 万人,死亡病例达5000 多例,波及120 多个国家,已形成全球大流行的事实.
为研究新型冠状病毒(COVID-19)的传播规律,全世界的医务工作者和生物数学的科研工作者已投入其中.在武汉发生新型冠状病毒肺炎初期,Lin 等人[1]分析了最初的425 例确诊病例的临床资料,确定了新冠肺炎的一些流行病学特征.Chinazzi 等人[2]研究了旅游限制对新型冠状病毒爆发传播的影响,使用全球集合种群疾病传播模型来预测旅行限制对该流行病的国内和国际传播的影响.Lin 等人[3]考虑了个人的行为反应和政府的行动,提出了一种SEIRNDC 概念模型,研究了疫情的发展趋势.黄森忠等人[4]运用SEIR 模型对新冠肺炎疫情进行了预测并对控制策略的效率进行了评估.唐三一等人[5]提出了新型的七仓室的离散随机模型,分析了不同的参数对疾病二次爆发风险的影响并给出了相应策略.严阅等人[6]提出了基于时滞微分方程的传染病模型并模拟了疫情的趋势.王霞等人[7]构建了复杂网络模型对武汉周边地区何时复工进行了研究.Yang 等人[8]提出了一种修正的SEIR 模型,得到中国的疫情将在2 月底达到顶峰,4 月底呈现逐渐下降的趋势,如果推迟5 天实施封城中国大陆的疫情规模将会扩大3 倍.还有一些医务工作者进行了临床研究[9–14].然而,现有的研究都是基于常微分方程、时滞常微分方程或是统计方法和临床病例研究,没有考虑到个体的空间扩散.事实上,空间扩散模型更能反应新型冠状病毒在时间和空间上的传播动力学规律.因此,本文主要是基于空间扩散的新型冠状病毒肺炎模型研究武汉的早期传播情况.
本文主要研究了武汉市2020 年1 月5 日之前的新型冠状病毒传染病的传播动力学,本文的传染病数据是2019 年12 月8 日至2020 年1 月5 日武汉市首批105 例确诊病例(数据来源于文献[1]).在传播早期,国家和武汉市还没有采取严格措施,可以认为人在空间上是自由扩散的.基于此我们建立了含有空间扩散的传染病模型,结合现有的文献及各种新闻报道,基于早期染病者数据和最小二乘法,我们对反应扩散方程进行了参数估计,找到了模型的最优参数,分析了染病者数量和潜伏者的扩散系数的敏感性.
本文的结构如下:第2 部分基于空间扩散建立了反应扩散传染病模型,并对模型的参数进行了解释,第3 部分针对模型我们给出了主要结果,包含参数估计和参数的敏感性分析,第4 部分给出了结论.
2 模型
在新型冠状病毒传染病传播的初期,不考虑人口动力学,即没有自然出生和死亡.目前所见传染源主要是新型冠状病毒感染的患者,且潜伏期具有传染性,传染途径主要是接触传播.根据流行病学特征,我们将研究人群分为:易感者S、潜伏者E、染病者I、移出者R 四类.这四类人群的转移关系可用仓室图1 表示.

图1: 易感者、潜伏者、染病者及移出者仓室转移图
考虑到空间各仓室个体的空间扩散,我们建立如下传染病模型
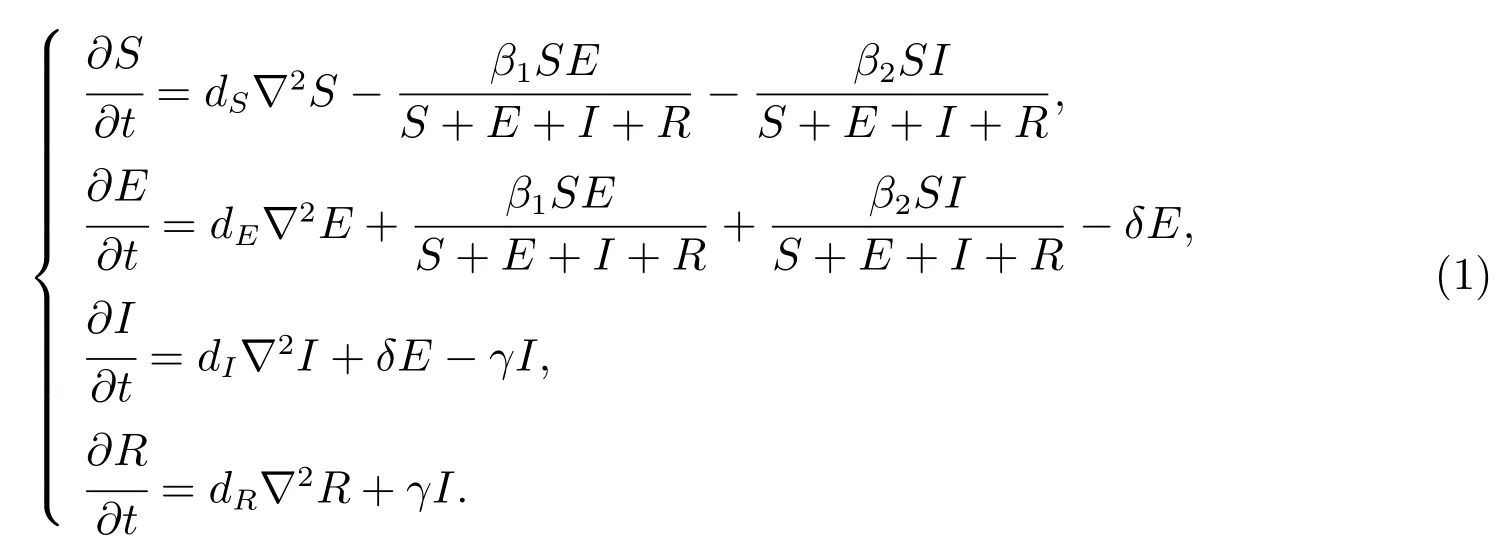
模型(1)各符号解释,见表1.

表1: 模型符号说明
在新冠肺炎传播的过程中,易感者与潜伏者或染病者接触会有一定概率的被传染.被传染的初期会有一定的潜伏期,经过潜伏期后转化为染病者,经过治疗或自我免疫会有一定比例的移出.接下来我们结合数据对模型进行研究.
3 主要结果
3.1 参数估计
本节将对模型(1)进行参数估计,方法基于最小二乘估计.具体过程是先将模型离散化,对时间的导数使用向前差分,空间二阶导数使用中心差分格式,得到模型离散格式

模拟时,我们将武汉市假设成一个方形区域[0,102]×[0,102],选取网格剖分
xi=ih, i=0,1,2,··· ,M, Mh=102,
yj=jh, j =0,1,2,··· ,M, Mh=102,
tn=100nτ, n=0,1,2,··· ,N.
研究武汉市早期新冠肺炎情况,可以考虑齐次纽曼边界条件(即零流边界),边界的离散格式为:左边界
S0,j=S2,j, E0,j=E2,j, I0,j=I2,j, R0,j=R2,j, 0 ≤j ≤M.
右边界
SM,j=SM−2,j, EM,j=EM−2,j, IM,j=IM−2,j, RM,j=RM−2,j, 0 ≤j ≤M.
上边界
Si,M=Si,M−2, Ei,M=Ei,M−2, Ii,M=Ii,M−2, Ri,M=Ri,M−2, 0 ≤i ≤M.
下边界
Si,0=Si,2, Ei,0=Ei,2, Ii,0=Ii,2, Ri,0=Ri,2, 0 ≤i ≤M.
模拟时将1500 万人口均匀分布在方形区域除边界的内部格点上,共有内部格点数为101×101 = 10201,所以初始时刻每个格点上易感者数量约为1470,基于目前的流行病学调查,潜伏期为1–14 天,多为3–7 天(出自中国疾控中心文件《新型冠状病毒肺炎公众防护指南(第2 版)》[15]).我们取潜伏期中位数(5 天)得到δ = 0.2,染病者的移出率[16]γ = 0.05,由于新型冠状病毒肺炎初期人们对疾病了解甚少,潜伏者可能表现轻微症状使其活动能力较正常人低,会引起潜伏者的扩散速度低于易感者,染病者以发热、干咳、乏力为主要表现,一部分患者同时伴有鼻塞、流涕、咽痛和腹泻等症状,会导致染病者的扩散速度小于潜伏者的扩散速度,参考移出者的实际情况,我们假设这四类人的扩散速率有关系dS> dE> dR> dI.模拟时分别取dS= 10, dE= 9, dR= 1.5, dI= 1,假设潜伏者的传染率与染病者的传染率相等,在首个患者被确诊时假设已有潜伏者数量E =5.模拟时时间步长和空间步长分别取为τ =0.01 和h=1.
记
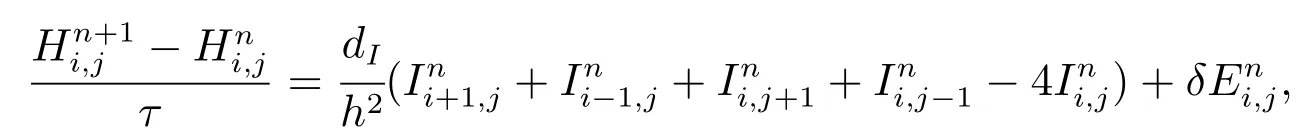


图2: 单点爆发下局部模型的染病者和真实统计数据随时间的变化情况

图3: 潜伏者随时间在空间中的分布情况
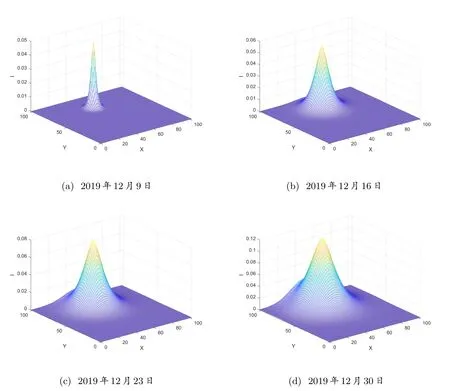
图4: 染病者随时间在空间中的分布情况
3.2 参数敏感性分析
为了更好的控制传染病的传播,需要研究模型中各个参数对染病者数量影响的大小.若其余参数固定的情况下改变某一个参数的值引起染病者数量的相对改变量较大,此时称染病者数量对该参数敏感性较大,否则,称敏感性较低.本节我们将研究染病者累计数量对对潜伏者扩散系数dE、潜伏者的传染率β1、染病者的传染率β2的敏感性.由于这三个系数耦合在模型中,所以我们可以通过改变参数的数值,对模型进行数值求解,通过得到的整个空间上的染病者累计数量来研究敏感性的大小.敏感性指数的大小可以对疾病的防控措施提供一等的理论支持,对于敏感性较大的参数,疾病的防控要特别重视,敏感性的大小可以通过图形反应出来,下面我们将对潜伏者的扩散率、潜伏者和染病者的传染率进行敏感性分析,并根据敏感性的大小提出相应的预防和控制措施.
3.2.1 针对潜伏者的扩散率dE 的敏感性分析
任何一种人际传播的传染病,人口的自由扩散速度会影响传染病的传播.传染病防控重点是管理好传染源,切断传染途径,针对新型冠状病毒肺炎传染病,由于潜伏者也可以传播,所以传染源包括染病者和潜伏者.由于潜伏者前期无症状或是症状不明显,所以潜伏者不容易被发现,但潜伏者的扩散会引起传染病的传播,防控潜伏者的传播对疫情的防空非常重要.
我们固定参数值dS=10, dI=1, dR=1.5, β1=0.1316, β2=0.1316, δ =0.2, γ =0.05,潜伏者的扩散率dE分别取dE= 0, dE= 1 和dE= 10,得到2019 年12 月8 日到2010 年1 月5 日的敏感性.我们将结果展示在图5 中,为了更易看清楚染病者数量随潜伏者扩散系数的敏感性,将图5 中(a)的部分局部放大得(b)图.这幅图中清楚的看到,随着潜伏者扩散系数的增加染病者数量也在增加,再次说明控制潜伏者的空间移动对传染病的防控至关重要,若传染病的早期及时控制潜伏者的空间扩散可以有效降低染病者的数量.为居家隔离等措施提供了理论依据.
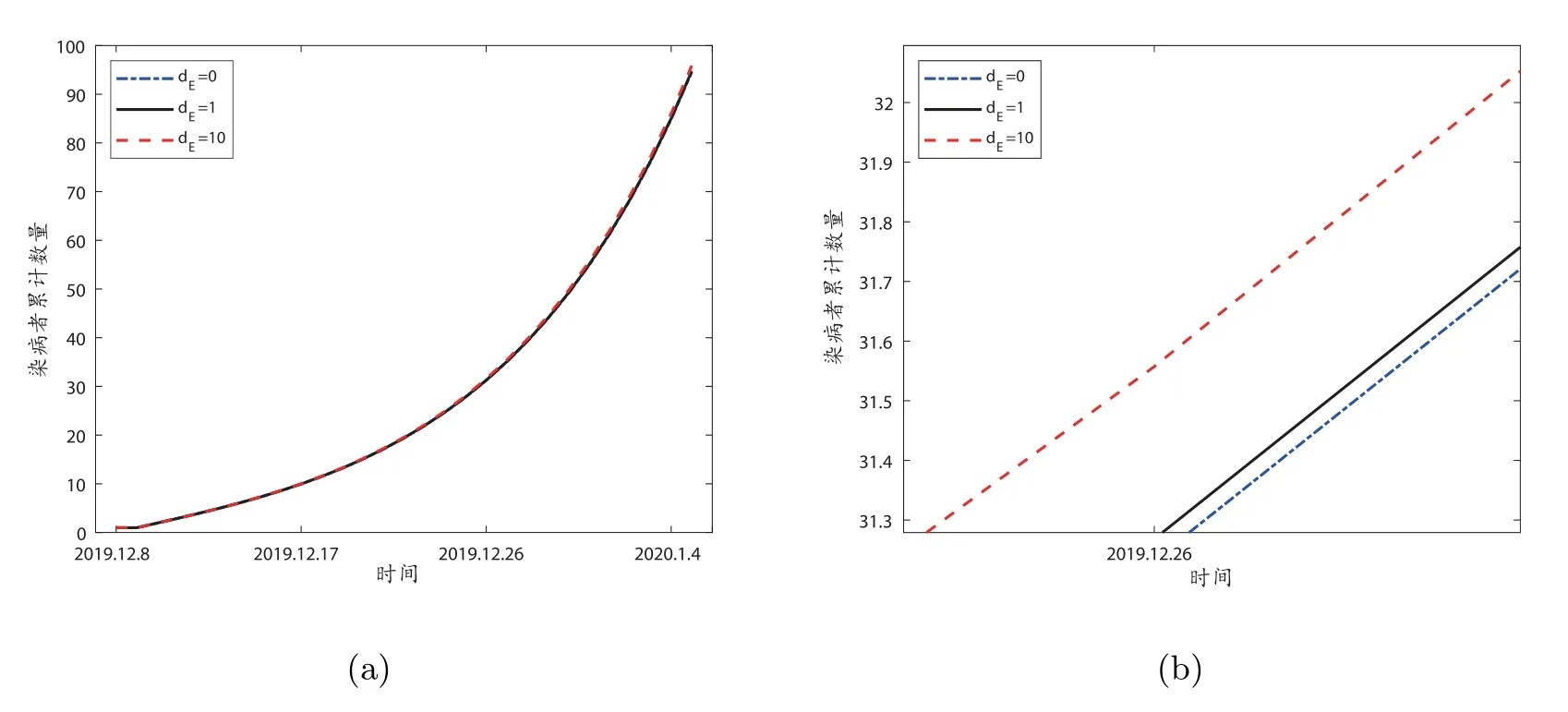
图5: 染病者数量对潜伏者的扩散系数的敏感性
3.2.2 针对传染率β1 的敏感性分析
我们固定参数值dS= 10, dE= 9, dI= 1, dR= 1.5, β2= 0.1316, δ = 0.2, γ =0.05,潜伏者的传染率β1分别取0.07, 0.1 和0.13,得到2019 年12 月8 日到2010 年1 月5日的敏感性.结果展示在图6 和图7 中.从图中可以看出染病者数量随潜伏者的传染率增大而增加,所以为防止新冠肺炎的传播应控制潜伏者的传染率,尽量减少与潜伏者的接触.所以早期居家隔离,减少去公共场所,减少走亲访友都是有效降低接触率的有效措施.
3.2.3 针对传染率β2 的敏感性分析
我们固定参数值dS= 10, dE= 9, dI= 1, dR= 1.5, β1= 0.1316, δ =0.2, γ = 0.05,染 病 者 的 传 染 率β2分 别 取0.12, 0.15 和0.18,得 到2019 年12 月8 日到2010 年1 月5 日的敏感性,结果展示在图8 和图9 中.从图中同样可以看出,染病者的数量随染病者传染率的增大而显著增加.在这个意义上而言,如何降低染病者的传染率是传染病防控的重要课题.比如外出佩戴口罩,减少无必须去医院的次数,对染病者及时进行集中隔离,对染病者接触人员进行有效追踪及时隔离等措施都可以有效控制染病者的传染率.

图6: 染病者数量对潜伏者传染率β1 的敏感性

图8: 染病者数量对潜伏者传染率β2 的敏感性
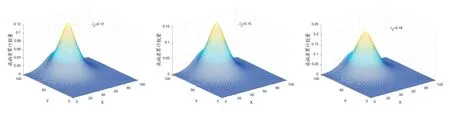
图9: 染病者数量对潜伏者传染率β2 的敏感性(2020 年1 月3 日的空间分布),从这三幅图中可以看出随β2 的增加,每个固定位置的染病者数量同样会升高,并且会有更多的空间位置出现染病者,意味着新冠肺炎会随传染率的升高而向空间四面八方扩散
4 结论
本文研究了新型冠状病毒(COVID-19)肺炎在武汉早期传播情况.在武汉封城之前,所有个体在空间上都是自由的,可以认为个体是随机游走,在空间上存在着扩散行为.基于此,我们建立了含有空间扩散的反应扩散方程传染病模型,在假设潜伏者和染病者的传染率相同的情况下,通过参数估计寻找到了最优的传染率.对模型采用有限差分格式进行了数值模拟,染病者和潜伏者随时间在空间中的传播情况我们通过三维图形进行了呈现.并对潜伏者的扩散系数、潜伏者的传染率和染病者的传染率进行了敏感性分析,结果显示对扩散系数敏感性偏小,对传染率的敏感性较大,所以在疫情防控方面要不仅要控制患者的扩散,而且需要重视如何降低潜伏者和染病者的传染率.因此,为了有效防控新型冠状病毒肺炎,应该尽量不去传染病爆发的区域,避免直接与患者的接触,做好充分的保护措施,减少外出暴露机会.对于突发传染病,早发现早隔离,及时切断传染源,有效降低传染率是防控防治传染的重要举措.
本文聚焦于研究传染病的早期传播特征,即没有干预措施或者干预措施不明显的时间阶段.而对于后期防控和治疗的介入,所构建的反应扩散模型是需要修正的.比如,居家隔离使得人群在空间无法形成扩散,进而使得人群以不同的社区尺度被隔离,需要研究传染病在社区是如何形成传染的.在这种情况下,基于复杂网络的集合种群模型更适合去描述传染病的传播.

