四阶Cahn-Hilliard 方程的间断有限元方法

邹乐强, 刘丽杰, 韦雷雷

(1- 河南工业和信息化职业学院，焦作 454000; 2- 河南工业大学理学院，郑州 450001)

1 引言

在本文中，我们考虑如下的四阶Cahn-Hilliard 方程

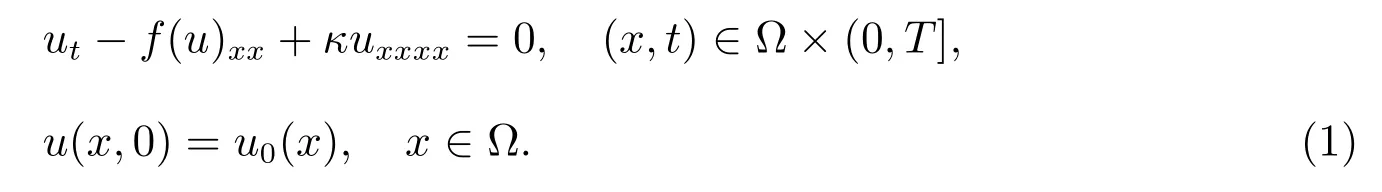
考虑周期边值条件，其中κ ≥0, Ω ∈R，f(u)是光滑函数.注意到这里周期边界条件的假设仅仅是为了问题讨论的简单，并不是本质的，间断有限元方法能够直接推广到非周期边值问题.

四阶的Cahn-Hilliard 方程首先是由Cahn 和Hilliard[1]于1958 年在研究二元合金的分离现象时提出的，随着现代科学技术的不断发展，该方程的应用也越来越广泛，如多相流中的界面动力学.一些学者对四阶Cahn-Hilliard 方程的数值方法有着浓厚的兴趣，如有限元方法[2–12]，间断有限元方法[13–16]，多重网格法[17–19]以及有限差分法[20–22].本文的主要工作是对四阶Cahn-Hilliard 方程构造一种间断有限元格式，并进行了理论分析和数值测试.我们所设计的间断有限元方法与文献[13–16]中所使用的是不同的.在文献[13]中作者所使用的数值方法，是在时间上运用间断有限元方法进行离散，而本文所考虑的是在空间上进行间断有限元方法离散.文献[14]中所研究的是局部间断有限元方法，与我们所构造的方法是不同的.在文献[15]中作者用标准的C0有限元形函数.在文献[16]中所使用的是一种内罚间断有限元方法.

间断有限元方法的基函数是完全间断的分片多项式，将分片多项式空间作为近似解和试验函数空间，目前该方法已在许多领域中得到应用，如气象学、天气预报、涡轮机、湍流、浅水波模型、海洋学、气动力学、粒子流、石油勘探、磁动力学、电磁学等.最初间断有限元主要用来解决双曲问题，后被推广到其他问题中，得到了很好的结果.间断有限元方法具有一致高精度的特点，而且通过选取单元插值多项式的次数，就可以提高数值精度，在实现p 自适应方面，具有很大的优势[23].同时由于解的间断性假设，对网格正则性的要求并不是很高，所以该方法不需要考虑传统有限元方法中连续性的限制条件，就能够对网格进行处理，很容易实现h 自适应.间断有限元方法具有非常好的局部紧致性而且易于实现并行计算.

2 符号和理论结果

这部分将介绍一些文中要用到的符号和一些理论结果.

为方便起见考虑一维情形，Ω=[a,b]，对网格进行剖分

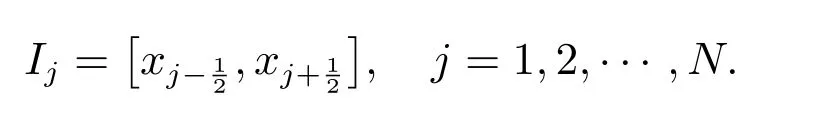
区间的中点为

区间长度为

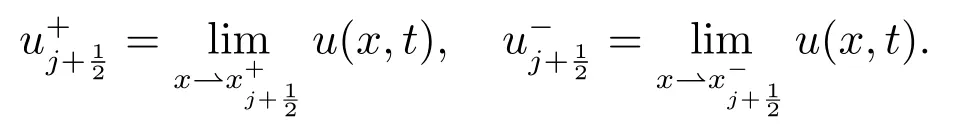
定义如下的有限元空间

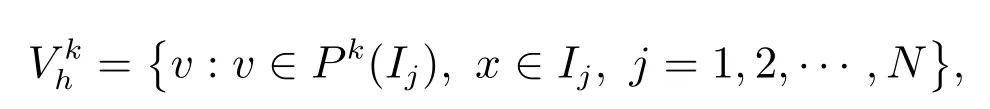
其中Pk(Ij)表示Ij上次数不超过k 的多项式集合.

对任意的vh∈Vkh，存在与vh和h 无关的λi(i=1,2,3)，使得

其中τh表示单元端点的集合，对以上性质的详细证明可参考文献[24].

如果k ≥4，我们可以选取空间Vkh上的投影Ph，使得对任意的u, Phu 满足

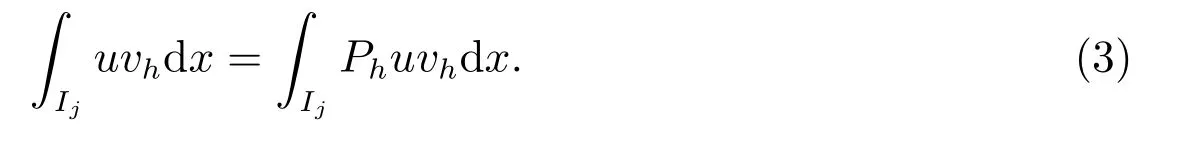
对任意的vh∈Vk−4h，且

令η =u −Phu 表示投影误差.由逼近论[25–27]，可以得到

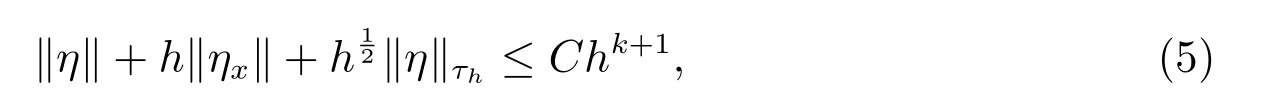
其中C 与h 无关，∥η∥τh表示在τh上的L2范数

3 间断有限元方法

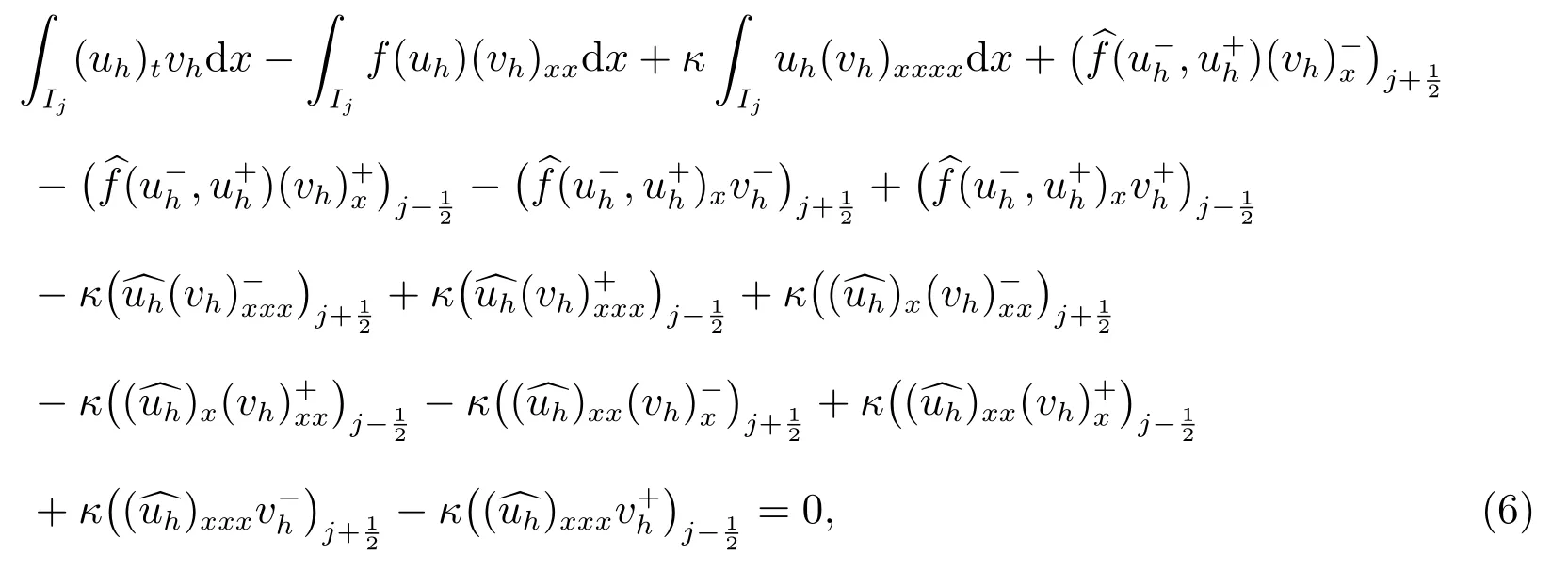
对任意的vh∈Vkh, j =1,2,··· ,N.

这里带“∧”的项是数值流通量，可以选取

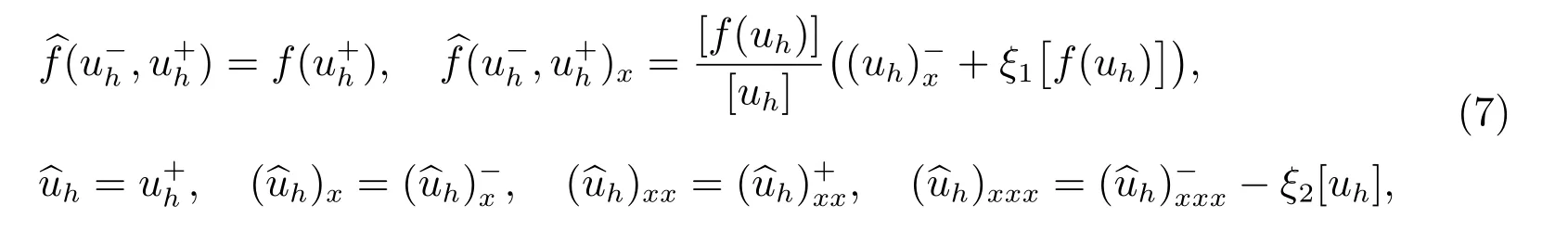
这里ξ1, ξ2是很小的正数，阶分别为O(h−1), O(h−3).与传统的局部间断有限元方法相比，我们可以看到在流通量中出现了ξ1[f(uh)]和ξ2[uh]等惩罚项.为了格式的稳定性，这些惩罚项是必须的.

3.1 稳定性

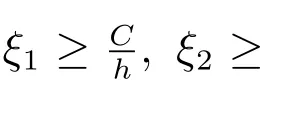
∥uh(t)∥≤∥uh(0)∥.

证明 在格式(6)中，我们取vh=uh，关于j 相加，可得

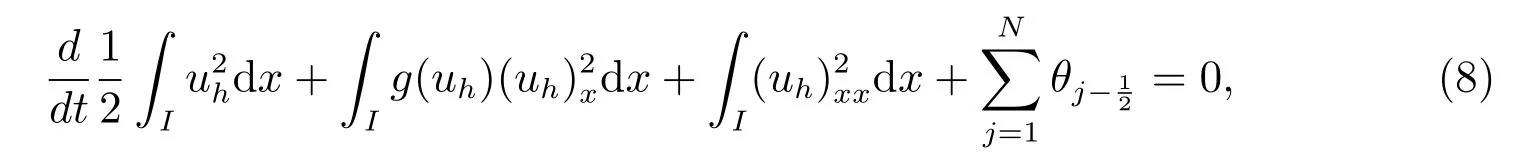
其中

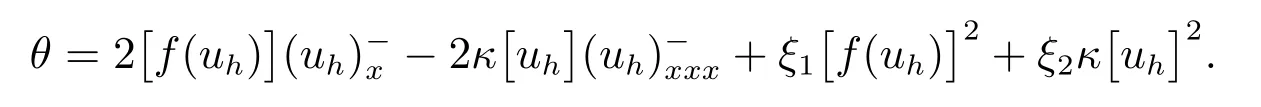
由(8)，可以得到

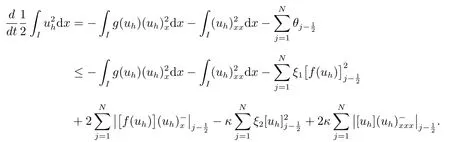
运用性质(2)，可知存在常数C，使得

由Young 不等式，可以得到

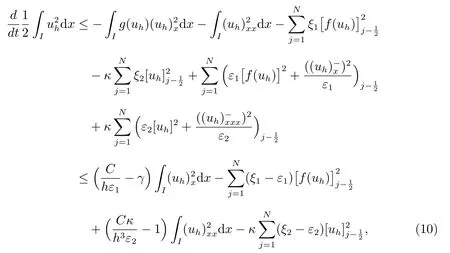
其中ε1, ε2>0.

令

上式(10)可化为

对上式两端从0 到t 关于时间做积分，可得

∥uh(t)∥≤∥uh(0)∥.

3.2 误差估计

我们考虑线性情况f(u)=u 时格式(6)的误差估计.

定理2光滑函数u 是问题(1)的精确解，uh是格式(6)的数值解，数值流通量为(7)，在周期边界条件下，当k ≥3，我们有下面的误差估计结果

∥uh(t)−u(t)∥≤Chk−1.

常数C 依赖于k, t, ∥u∥，与h 无关.

证明 令e=u −uh表示数值解与精确解之间的误差，我们可以得到如下的单元误差估计∫

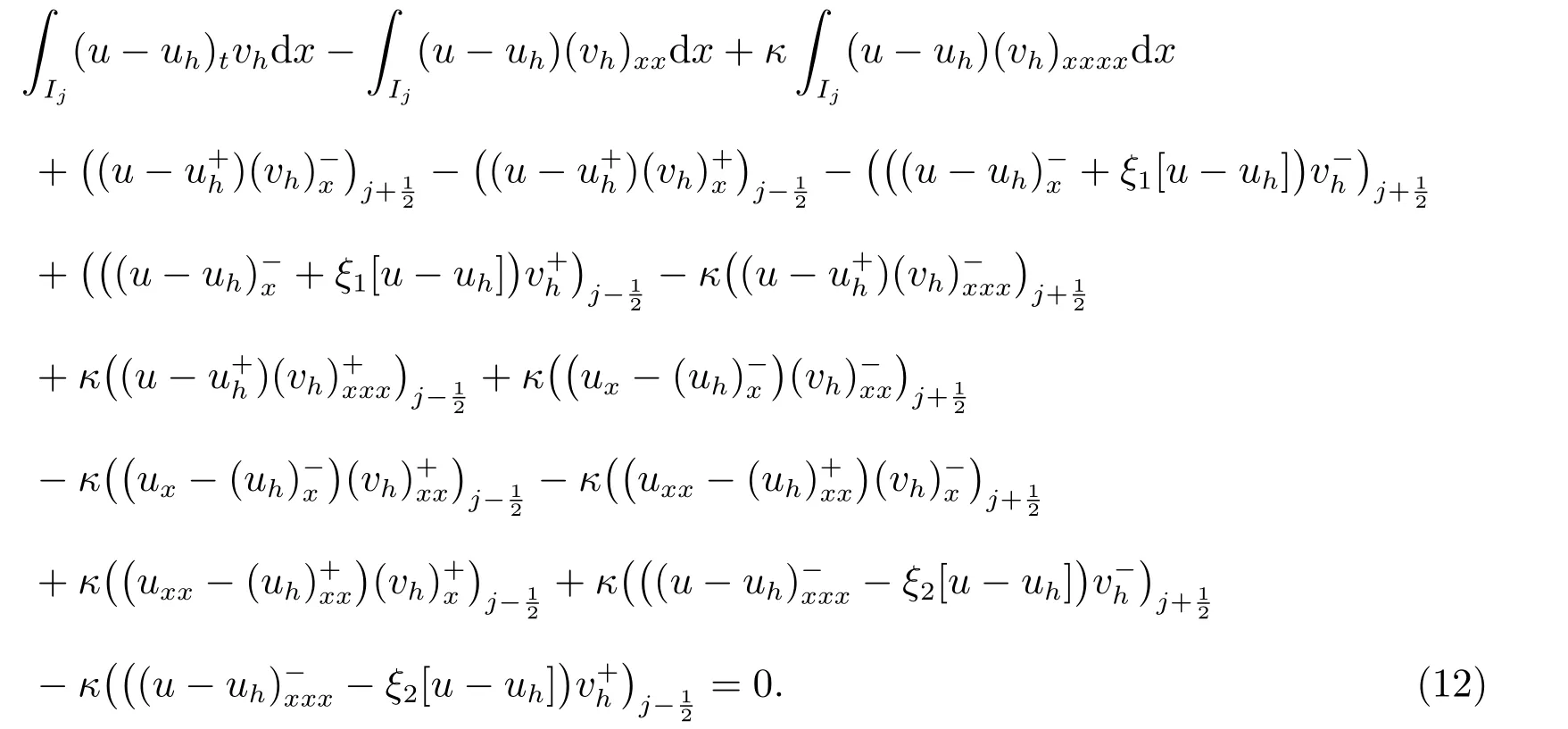
为简单起见，定义符号

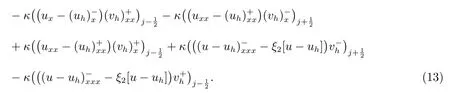
令wh=Phu −uh, we=Phu −u.取vh=wh，可得

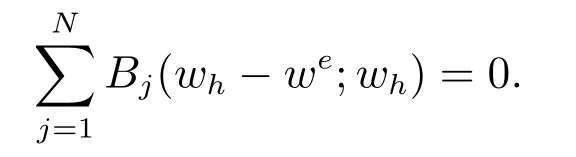
当k ≥4，上面式子的左边为

由投影性质(3)–(5)和稳定性结果，可得

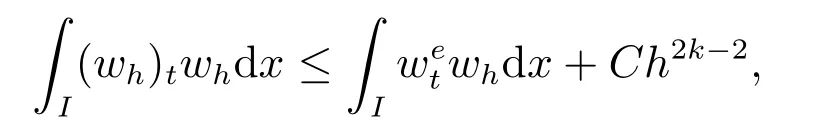
即

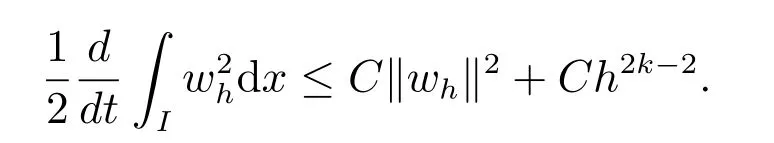
当k ≥4 时，定理2 得证.

当k =3 时的证明和k ≥4 的方法类似.所不同的是我们采用另外一种投影Qh：对函数u,

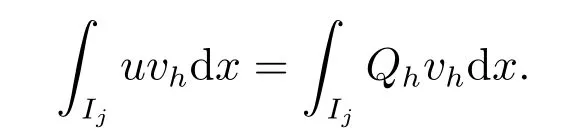
对任意的vh∈V0h，而且

由逼近论[24]，可得

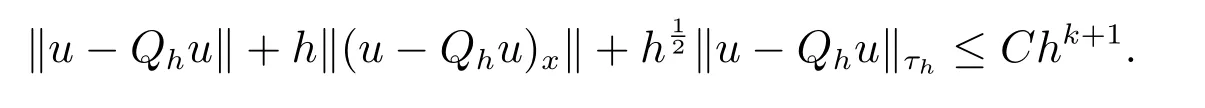
同样定义wh=Qhu −uh, we=Qhu −u，可得

根据稳定性结果，我们可以得到

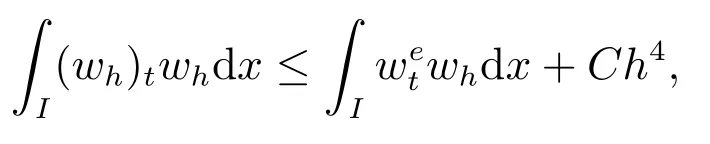
可知

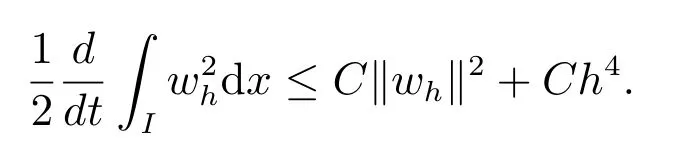
当k =3 时，定理2 得证.

4 数值算例

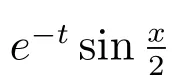
表1: 间断有限元格式(6)的精度测试结果，T =0.5

5 总结

在本文中我们研究了四阶Cahn-Hilliard 的间断有限元方法，证明了方法的稳定性和收敛性.该方法不同于传统的局部间断有限元方法，不需要引进额外的辅助变量或将方程写为一阶的方程组，能够减少计算量和存储量.下一步，我们计划将该方法推广到其他含有高阶导数的问题，并考虑与交替方向法结合来数值求解高维问题.