不同铅浓度土壤XRF光谱的频率域去噪及规律研究

付萍杰， 杨可明， 刘浦东*

1. 山东建筑大学测绘地理信息学院， 山东 济南 250101 2. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室， 北京 100083

引 言

土壤是人类生产生活、 万物依存的关键载体， 是参与生态系统循环的主要组成部分[1-2]， 也是一种极其重要的自然资源。 由于一些人为干扰及自然原因， 土壤中重金属浓度将逐渐增大， 当土壤中重金属浓度超过了当地环境背景值时， 其累积效应会影响土地承载力， 长此以往致使土壤中重金属浓度远远高于原生态的浓度， 最终导致土壤重金属污染， 引发生态环境恶化。 近年来， 全球工业的快速发展和城市化的推进引发了一系列环境问题， 其中土壤重金属污染备受关注[3]。

铅(Pb)是高毒性重金属， 荧光传感器能够高效、 准确地检测Pb浓度[4]， 因此引入荧光光谱对Pb重金属浓度进行高效测量。 基于荧光强度与Pb重金属浓度之间的线性回归模型， 采用便携式X射线荧光光谱仪(portable X-ray fluorescence， PXRF)进行综合检测是测量土壤Pb总浓度的有效技术方案[5]。 X射线荧光(X-ray fluorescence， XRF)光谱具有成本低、 分析速度快、 操作简单、 可同时分析多类重金属且适合大面积监测[6]等优势， 已被广泛应用于土壤、 纺织材料、 农作物产品、 矿产等重金属监测和环境质量评价中[7]， 效果显著， 相关研究研究成果取得一定进展[8]， 充分突显了XRF光谱巨大的应用发展前景。

近几年， 随着PXRF光谱仪精度的不断提高， XRF光谱分析在土壤重金属检测中的应用研究日渐趋广。 彭洪柳等将高精度PXRF光谱仪所测得的土壤中Cu、 Pb浓度与传统的仪器所测的Cu和Pb浓度做对比， 发现高精度PXRF光谱仪所测得的数据精度较高， 决定系数高达0.997 5[9]。 Kodom等利用XRF光谱分析检测六个采样点0～15 cm的表层土壤中Zn， Pb， Cr， Cu， Co， Ni， Cd， Hg和As的浓度， 评价土壤环境质量[10]。 有研究利用NITON XLt 793型PXRF测量并分析了Pb元素的XRF光谱特征， 研究了10.55和12.61 keV处Pb特征谱线强度与Pb浓度的关系。 有报道利用PXRF检测原位及实验室条件下土壤样品包括Pb和Cu在内的多种重金属浓度， Pb和Cu的检出限分别为8.1和10.6 mg·kg-1。 邝荣禧等分别利用PXRF和传统的实验室化学分析方法测量土壤中As， Pb， Cu和Zn四种重金属浓度， 两种测量方式得到的结果具有一致性， Pb和Cu的决定性系数均大于0.70， PXRF法可以快速检测矿区周边土壤的Pb和Cu浓度[11]。 Salazar等使用全反射X射线荧光(total reflection XRF， TXRF)光谱分析土壤和植被中Pb， Cu和Zn重金属浓度， 用于研究植被对受污染土壤的Pb的吸收情况[12]。 Lintern等利用PXRF测量方法， 检测历史洪水的沉积岩芯中包括Cu和Pb等6种重金属浓度， 作为一种经济高效方法替代了广泛的现场监测[13]。 杨桂兰等利用PXRF检测土壤中包括Cu和Pb在内的6种重金属含量， 根据最低检出限和检测灵敏度， 发现该仪器对Pb元素的检测灵敏度最高， Cu的检测精度仅次于Pb[14]。 Hu等使用PXRF光谱仪测定中国长江三角洲地区浙江省富阳市301个农田土壤重金属污染， 研究结果表明， 该方法可以快速准确预测土壤中Zn， Cu和Pb的浓度， XRF光谱在Lb1和Kb1的Pb特征能量分别分布在12.614和84.936 keV处， Cu特征能量分别分布在0.93和8.905 keV[15]。

近年来， 随着PXRF光谱仪精度的提高， XRF光谱在土壤Pb重金属浓度检测方面优势日趋明显， 并已取得大量成果， 但研究内容大多集中在土壤Pb重金属浓度测量结果的精度评价和环境质量评估， 而对于土壤XRF光谱差异特征变化的深入分析研究较少。 时频分析技术可将时域中复杂的信号变换为频域空间的简化信号， 从频率域角度检测电磁信号中存在的异常信息， 其中， 谐波分析(harmonic analysis， HA)可用于电磁信号的噪声去除； SPWVD(平滑伪魏格纳分布)事先选择合适的基函数， 突出信号原有的时频局域性， 对局部细节的表达更为精细。 本研究通过引入时频分析法对土壤XRF光谱特征信息进行甄析， 首先采用HA方法探究土壤XRF光谱的去噪效果， 然后利用SPWVD研究实地采样土壤样品的去噪XRF光谱， 得到该地区土壤Pb浓度超过当地土壤环境背景值(超标)样品的频率域变换光谱局部规律， 并探究土壤Pb浓度超标样品的XRF光谱的特征波段， 以期实现从新的角度去分析挖掘XRF光谱特征的规律。

1 实验部分

1.1 土壤采样

本次研究所使用的实地采样样品为内蒙古自治区锡林浩特市锡林郭勒盟某煤矿区周边(44°00′13.34″N， 116°00′18.21″E)的土壤(图1)， 使用锹采集0～20 cm深度的表层土， 每个样品重复2点点位， 样品采集范围主要分布在矿区内部、 矿区周边(东北部、 南部、 东部)的排土场、 矿区西部的河床以及部分牧民家用地， 共采集样品32份(分别标记为SL#1， SL#2， …， SL#32)， 每份样品重量约为2.5 kg。 对每份样品进行均匀混合及过5 mm筛预处理后， 进行土壤XRF光谱数据获取及Pb浓度分析。

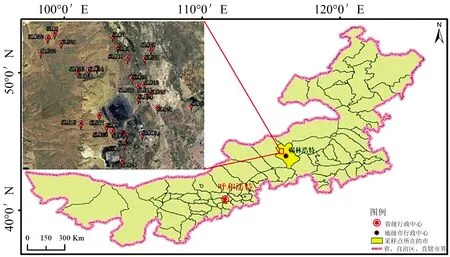
图1 野外实地采样土壤样品分布

1.2 土壤XRF光谱及Pb浓度数据获取

使用Niton XL3t 950 PXRF光谱仪采集土壤样品XRF光谱， 并对土壤样品进行化学分析， 测量土壤样品中重金属的浓度。 该光谱仪是Niton XL3t系列的一种， 仅需瞄准、 测试， 数秒内便可检出矿石中Cu， Zn和Pb等40多种元素的含量， 并可实时显示分析数据、 图谱。 检测精度接近实验室级的分析水平， 可分析极低含量(ppm级)至高百分比含量(%)， 而且样品在整个测试过程中无任何损坏。 该仪器具有特殊构造， 采用坚韧的LEXAN塑料密封外壳， 重量轻、 坚固耐用， 密封式一体化设计， 防尘、 防水、 防腐蚀、 抗冲击， 可在任何地方安全使用。

首先， 进行仪器检校， 使用Niton XL3t 950 PXRF光谱仪测取标准样品(设备自带的检校样品)中所含成分的浓度， 若所测结果与标准样品的官方给定结果一致， 则仪器检校完成， 可进行土壤样品测量， 若所测结果相差较大， 需进行返厂检修。 利用检校合格的Niton XL3t 950 PXRF光谱仪进行土壤样品XRF光谱及Pb浓度数据的分析， 由于不同土壤样品中化学元素及其含量的不同， 在XRF光谱不同波长(能量)处的谱线强度(元素含量)是不同的， 但因同一地区的土壤类型差异不大， 土壤XRF光谱并不存在明显差异， 不同土壤样品的XRF光谱数据见图2， 图中keV代表样品中包含的元素， 与元素的原子序数有关， Counts与元素含量有关。

根据前人的研究发现该矿区周围的土壤中重金属主要有Pb， Zn， Mn， Cu和Ni[16-17]， 因此， 本次研究重点选取Pb重金属进行分析。 本次实地采样采用电感耦合等离子质谱测得土壤Pb浓度的统计分析见表1， 根据测得的数据可以看出， 大多数样品的Pb浓度高于内蒙古自治区土壤环境背景值， 少数样品的Pb浓度低于内蒙古自治区土壤环境背景值。

2 理论与方法

2.1 谐波分解(HA)

HA最初由Jakubauska等提出， 并较多应用于机械及电力系统的信号检测等[20]。 根据谐波分析(HA)的定义， 可以将光谱的HA近似理解为以正(余)弦曲线的叠加， 即： HA将光谱分解为多个不同频率的谱线， 通过叠加不同频率的谱线来表示原始光谱。 合适的HA分解重构次数可以最大程度表达光谱特征， 达到良好的光谱去噪效果。 依据周期性波形的傅里叶展开形式， 对于离散的光谱曲线而言， 对其进行变换展开后可以表示成傅里叶级数的形式为式(1)

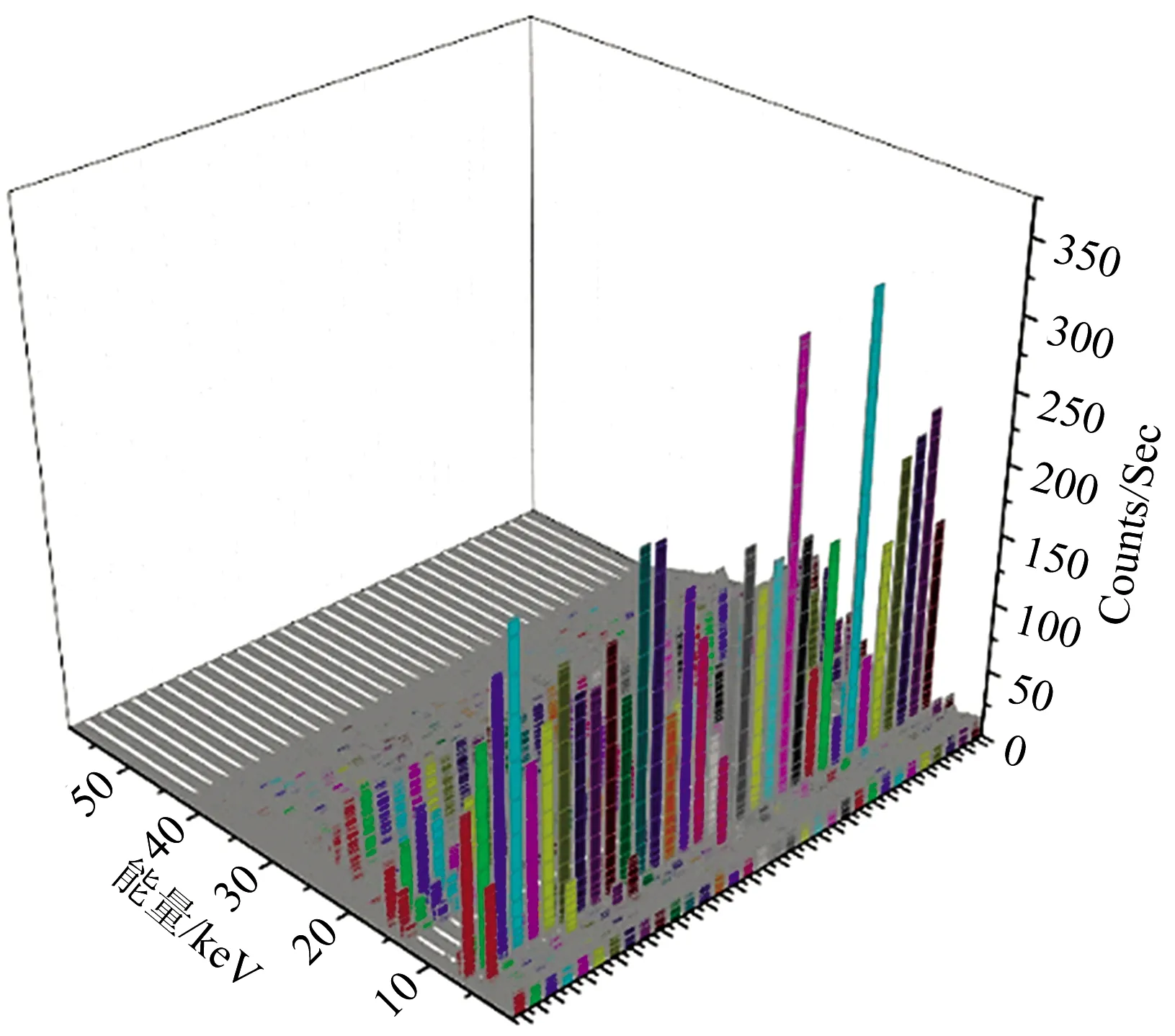
图2 不同野外实地采样土壤样品的XRF光谱

表1 实地采样土壤样品Pb浓度统计分析

(1)

式中，Chsin(2hπn/L+φh)为第h次谐波分量，Ah，Bh，Ch，φh的计算公式为

(2)

式中，x(n)为离散的光谱曲线；n为波段号数；L为波段总数；A0/2表示谐波余项；h为分解次数；Ch为第h次谐波分量的振幅；φh为第h次谐波分量的相位； 经过谐波变换后， 光谱曲线维数W=2h+1。

从式(2)可以看出， 每条光谱是由一系列正(余)弦分量曲线叠加而成的， 每条正(余)弦曲线又是由谐波余项A0/2、 振幅Ch和相位φh组成的， 对土壤XRF光谱进行谐波分解后， 可以得到不同频率的光谱分量(图3)， 选择合适的分解次数h， 累加所有的光谱分量就可以得到与原始光谱极尽相似的重构光谱。 其中， 谐波分解次数h≈W/2， 为了达到不同的光谱处理效果， 可以选择不同的分解次数。

2.2 光谱的平滑伪Wigner-Ville分布

近几年， Wigner-Ville分布在医学、 电气、 机械、 地震等信号的处理中得到了广泛应用[19]， Wigner-Ville分布在信号的频率域分析中是发展较为成熟的一种方法， 其表现为双线性类时频分布， 可有效提取信号的局部信息， 在信号局部能量聚集的时频联合分布的描述中具有一定优势。 将光谱曲线x(t)的Wigner-Ville分布定义为

(3)

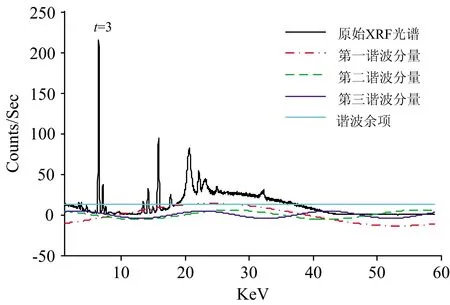
图3 土壤XRF光谱谐波分解示意图

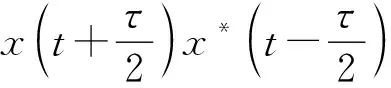
光谱Wigner-Ville分布相对于其他方法具有很好的时频聚集性、 较高时频分辨率及平移不变性等优点， 在光谱信号分析中优势明显。 但Wigner-Ville分布也有其自身缺点， 其时频分析结果在很大程度上受交叉项干扰影响， 结果中出现的一些虚假信号会影响时频分析结果的准确性， 掩盖光谱信号中的有效信息。 如果将一条光谱表示为两条光谱之和， 如：x(t)=x1(t)+x2(t)， 则

Wx(t,w)=Wx1(t,w)+Wx2(t,w)+2Re{Wx12(t,w)}

(4)

式(4)中，Wx是光谱x(t)的魏格纳分布，Wx1与Wx2分别是光谱x1(t)与光谱x2(t)的魏格纳分布，Wx12是光谱x1(t)与光谱x2(t)交叉项的魏格纳分布。

从式(4)中可以看出， 两条光谱和的魏格纳分布不等于每条光谱魏格纳分布之和， 而是还存在两条光谱交叉项的影响。 为了解决交叉项干扰的问题， 可以充分发挥核函数的作用， 在Wigner-Ville分布中同时加入频域窗函数和时域窗函数， 这样经过变换的Wigner-Ville分布就变为了平滑伪Wigner-Wille分布(smoothed pseudo Wigner-Ville distribution, SPWVD)， 计算公式为

h(τ)g(v)exp(-j2πfτ)dτdv

(5)

式(5)中， 核函数φ(τ,v)=h(τ)g(v)，h(τ)为频域窗函数，g(v)为时域窗函数， 且满足h(0)=G(0)=1，G(f)为g(t)的傅里叶变换。

以一组高斯模拟信号为例， 如图4所示， 分别使用Wigner-Ville分布和平滑伪Wiger-Ville分布对其进行分析变换， 相应的处理结果如图5(a,b)所示， 信号的Wigner-Ville分布中， 交叉项的存在会产生“虚假信号”， 掩盖有效信息， 而平滑伪Wiger-Ville分布消除了交叉项的影响， 突出了信号原有的时频局域性。

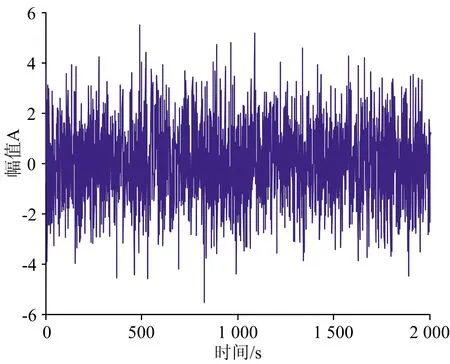
图4 高斯模拟信号

3 Pb浓度超标土壤样品XRF光谱的SPWVD规律

3.1 XRF光谱的谐波分解去噪

XRF光谱降噪是一种消除杂波干扰的有效方法， 高效的降噪方法对于提取光谱特征信息至关重要。 降噪方法多种多样， 其中， 频率域降噪方法效果理想， 主要包括： 小波分解、 经验模态分解(empirical mode decomposition， EMD)及谐波分解等。 谐波分解最早主要应用于电力系统检测[20]， 后来应用于信号去噪[21]。 在遥感领域， Jakubauskas最先提出使用HA分析遥感数据， 通过分析AVHRR NDVI时序数据描述了自然和农业土地利用的季节性变化， 并验证了HA在农作物物种识别中的有效性[22]。 随后， 与HA相关的遥感影像作物物候规律分析及目标探测等研究成果相继出现[23]， 但是HA在XRF光谱领域的应用研究尚未开展， 其降噪效果有待进一步探究。

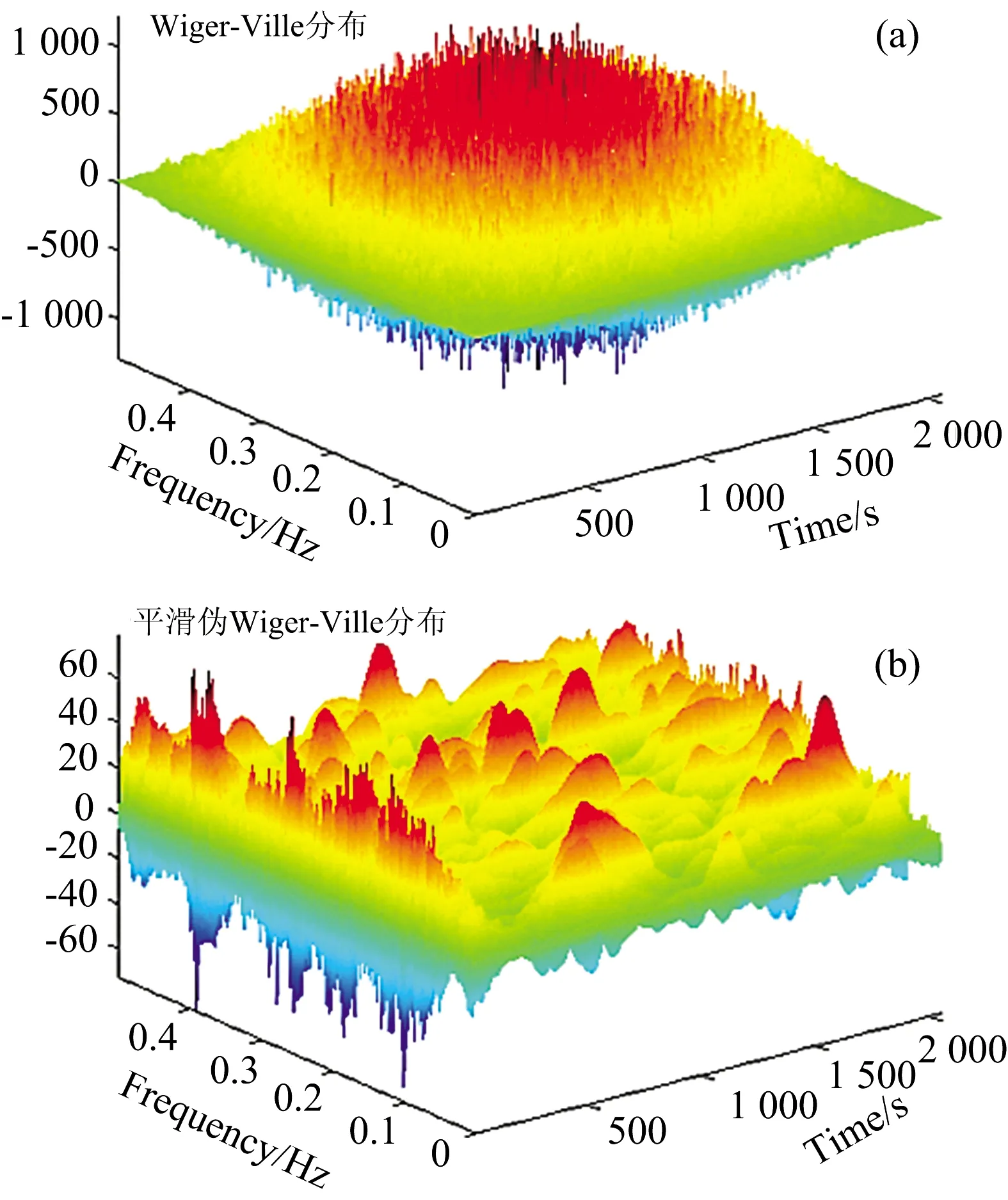
图5 高斯模拟信号的Wigner-Ville分布(a)及平滑伪Wiger-Ville分布(b)

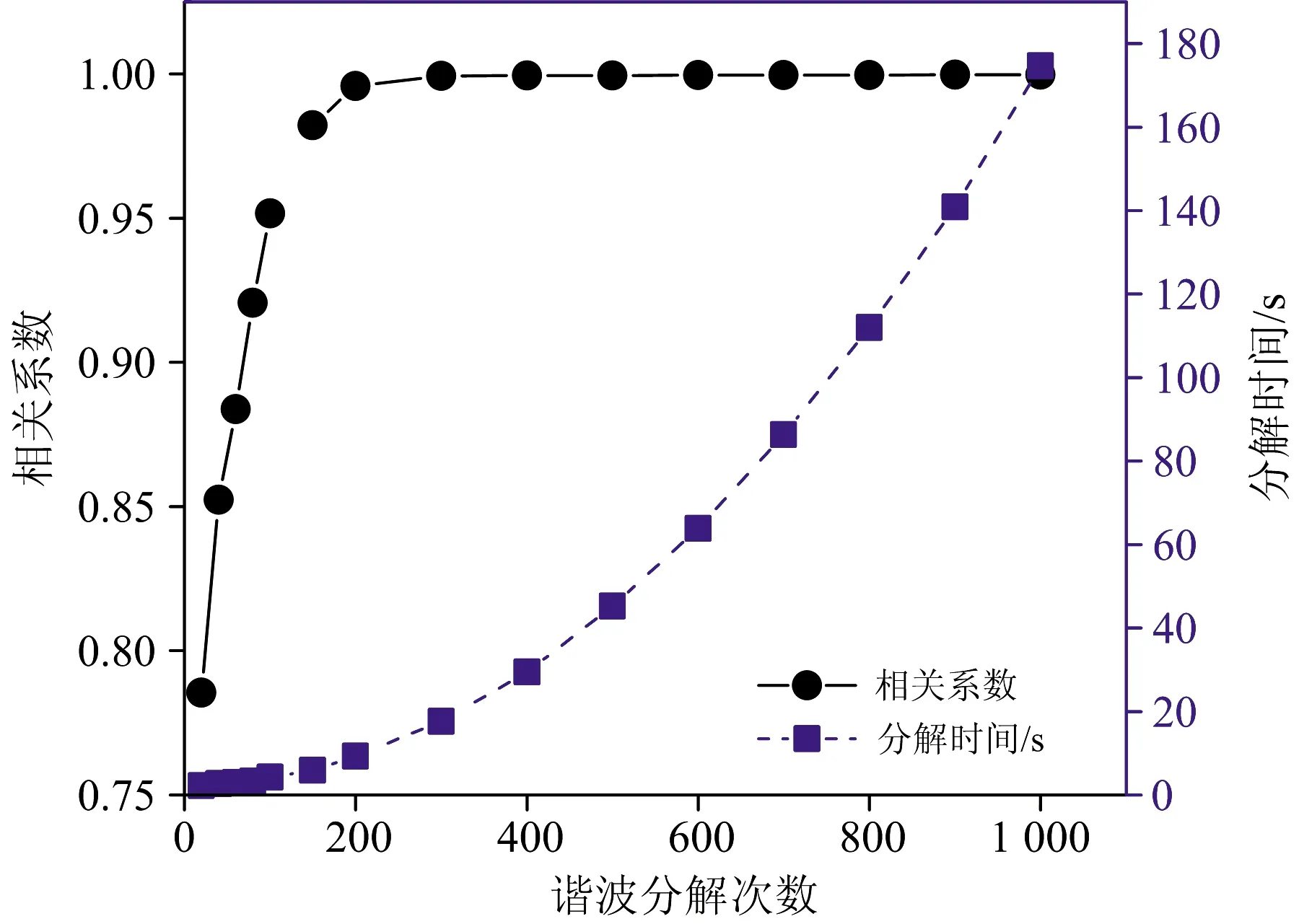
图6 不同分解次数下谐波重构去噪土壤XRF光谱与原始光谱的相关系数及分解所需时间

根据HA的原理及应用总结， 一般最佳的分解重构次数为波段数的一半。 本次实验得到的土壤XRF光谱的波段数为3 911， 则理论上需要分解近2 000次后进行重构， 但由于循环计算量大， 耗时较长， 且2 000次去噪效果不明显， 因而寻求具有可操作性的合适分解重构次数成为关键。 为此， 分别设置分解次数为20， 40， 60， 80， 100， 150， 200， 300， …， 1 000次对土壤XRF光谱进行光谱重构， 得到的重构光谱与原始光谱的相关系数及分解所需时间见图6。 分析图6发现， 以300次谐波分解次数为分水岭， 随着谐波分解次数的增加， 相关系数随之增大， 20， 40， 60， 80， 100， 150， 200和300次分解得到的重构光谱与原始光谱的相关系数分别为0.785 4， 0.852 4， 0.883 9， 0.920 7， 0.951 6， 0.982 3， 0.995 8和0.999 3， 相关系数呈指数增长， 分解重构所需时间增长缓慢； 分解次数为300次之后， 相关系数比较平稳， 基本保持不变， 而分解重构所需时间逐渐呈指数增长。

图7 土壤XRF光谱谐波分解噪声去除

不同分解次数下， 土壤XRF重构光谱见图7， 在80次分解之前去燥效果不理想， 30 keV之前会产生光谱特征弱化和振荡现象； 分解100～150次时， 在20 keV之间会产生光谱特征弱化和振荡现象； 分解次数处于200～300之间时， 在10 keV附近会产生光谱特征弱化和振荡现象； 分解300次时效果明显好转， 没有光谱特征的弱化， 但仍存在微弱振荡现象； 当谐波分解次数达到400时， 微弱的振荡现象消除， 分解得到的重构光谱与原始光谱的相关系数为0.999 5； 当分解次数大于400时， 相关系数基本趋于稳定， 同时不存在光谱特征弱化和振荡现象， 直到分解次数为1 000次时， 相关系数虽达到0.999 7， 但所需分解重构时间会呈指数增长， 效能不佳。 因此经试验， 当光谱谐波分解重构次数为400时， 既不缺失土壤XRF光谱特征， 又能最大程度消除锯齿状光谱噪声， 还能节省运行时间， 效能良好。

3.2 去噪XRF光谱的SPWVD规律

利用光谱的SPWVD方法分析该矿区周边经谐波分解去噪的土壤XRF光谱， 得到整个波段序列上XRF光谱的频率分布， 仔细研究32份土壤样品XRF光谱频率分布随Pb浓度的变化发现， 在0～2 000波段序列上不同土壤样品的XRF光谱频率分布具有规律性差异。 在土壤Pb浓度低于内蒙古自治区土壤环境背景值的8份样品中， 6份样品XRF光谱的SPWVD随土壤中Pb浓度的变化具有一定规律， 所占比率为75%； 土壤Pb浓度高于内蒙古自治区土壤环境背景值的24份样品中， 19份样品XRF光谱的SPWVD随土壤中Pb浓度的变化存在一定的规律， 所占比率为79.17%。 具体特征如下：

(1)Pb浓度不超标的土壤

经式(5)可得该矿区周边的Pb浓度不超标土壤样品XRF光谱的SPWVD， 如图8所示， 当Pb浓度不超标时， 土壤样品XRF光谱的SPWVD有两种情况： 第一， 在波段序列为400(能量为6.42 keV)附近有1个较高的频率峰值(频率小于400 Hz)[图8(a)虚线椭圆圈标注]； 第二， 在波段序列为400(能量为6.42 keV)附近有2个很强的频率峰值(频率大于400 Hz)[图8(b)虚线椭圆圈标注]。

(2)Pb浓度超标土壤

利用式(5)获取该矿区周边的Pb浓度超标的土壤样品XRF光谱的SPWVD， 根据图9虚线椭圆圈标注可得， 当Pb浓度超标时， 在波段序列为400附近有1个很强的频率峰值(频率大于400 Hz)， 并且在600～700(能量为9.42～10.92 keV)波段序列之间有3个层次明显的频率峰值分布。

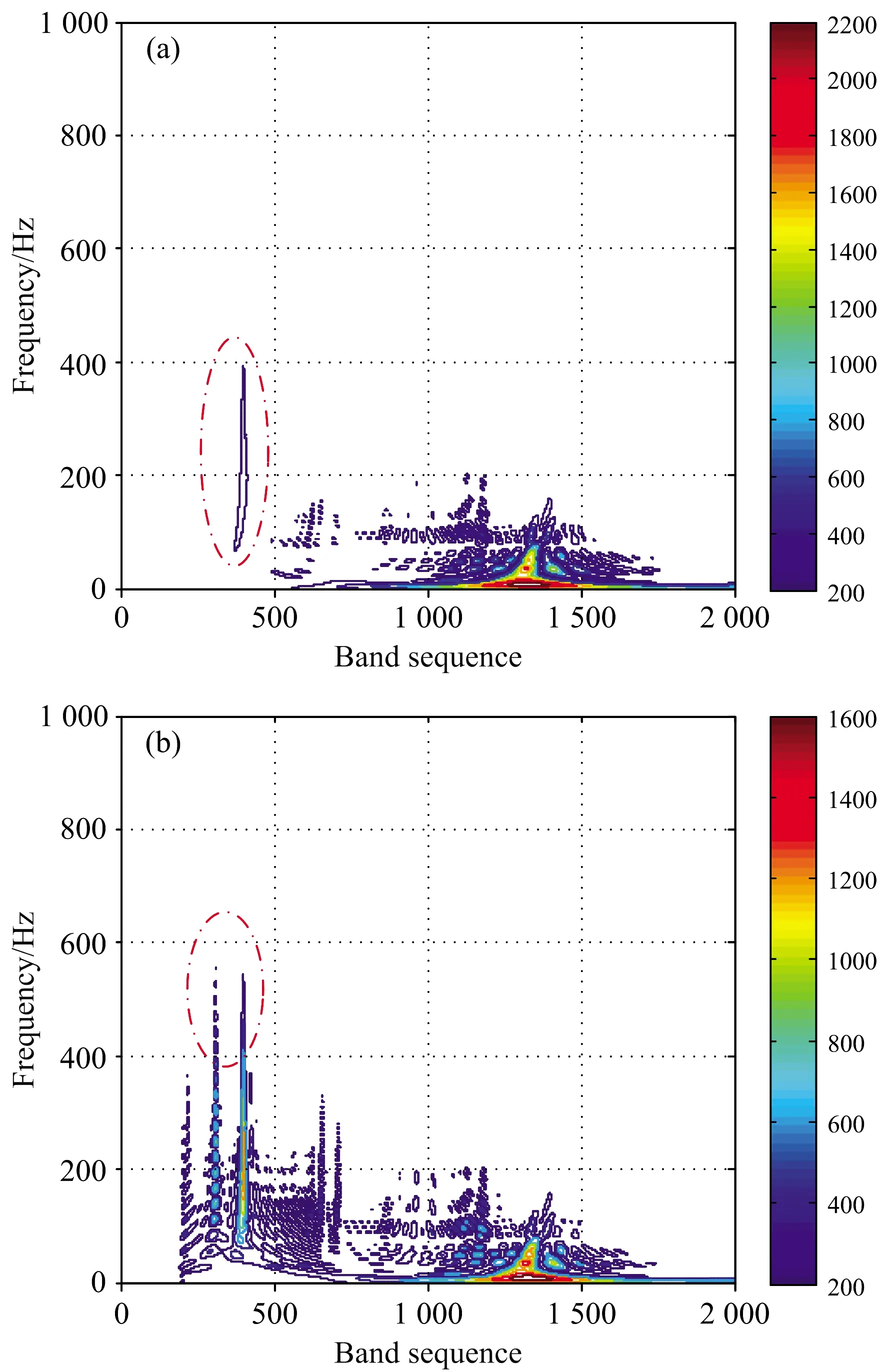
图8 Pb浓度不超标的土壤样品XRF光谱的SPWVD

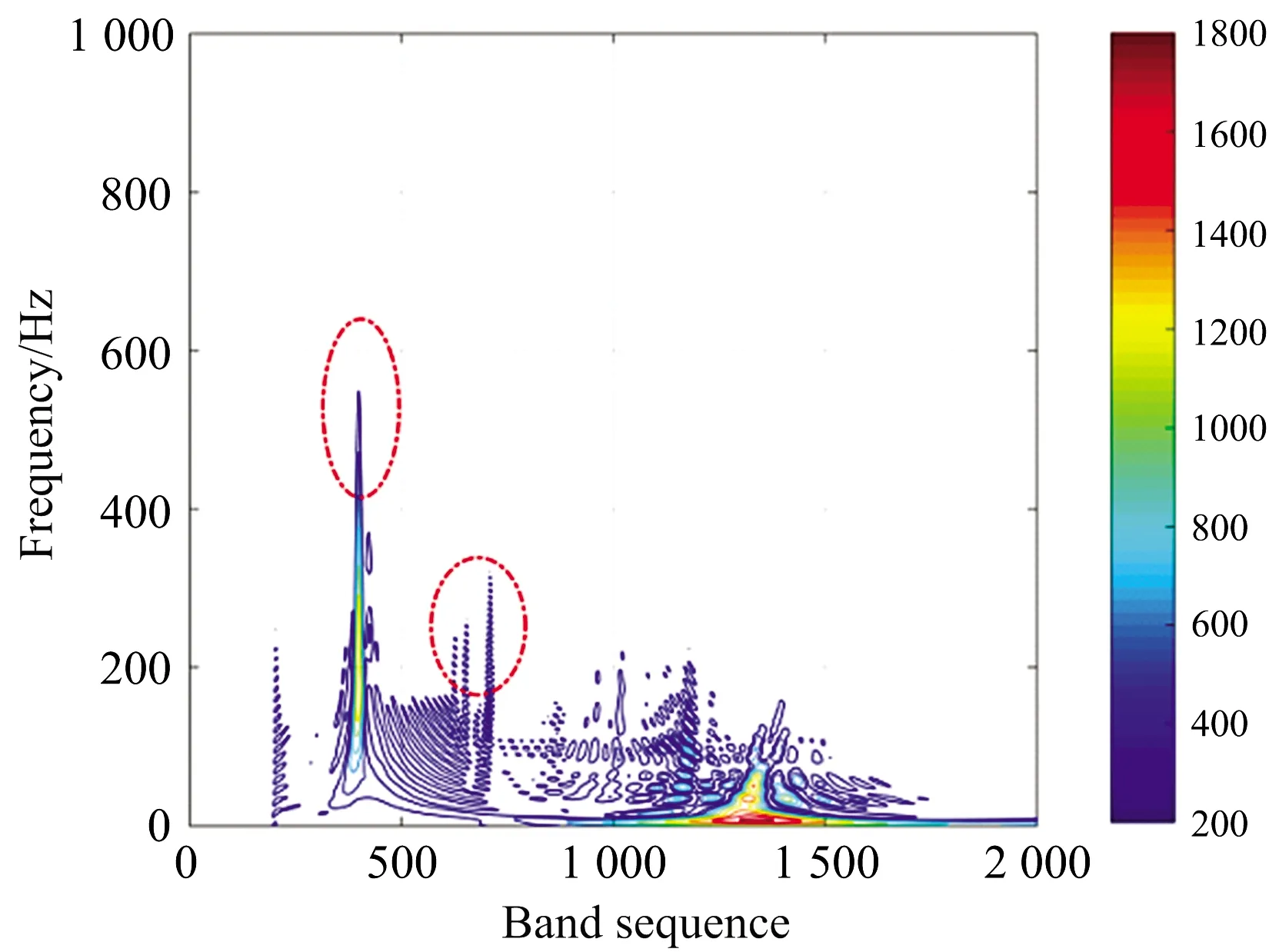
图9 Pb浓度超标的土壤样品XRF光谱的SPWVD

4 结果与讨论

4.1 XRF光谱谐波分解重构去噪方法的对比分析

经过对土壤XRF光谱进行HA， 分析比较了不同谐波分解次数下土壤XRF光谱的重构去噪效果， 得出当谐波分解400次时， 光谱的重构降噪效果理想。 为了进一步验证XRF光谱谐波分解重构去噪方法的性能， 将其与常用的两种频率域去噪方法EMD和小波分解重构去噪结果进行对比分析， 具体去噪效果如图10所示。

分析图10(a)发现， 由于EMD重构XRF光谱直接剔除含噪声信息量最大的固有模态函数(intrinsic mode function， IMF)IMF1分量， 重要的光谱特征信息被削弱， 并且出现振荡现象， 相比于HA重构降噪效果差； 同时， EMD重构XRF光谱与原始光谱相关系数为0.984 7， 相对于谐波分解较低。 由图10(b)可知， 小波分解重构得到的光谱与原始谱特征基本保持一致， 重构XRF光谱与原始光谱相关系数达0.999 6， 略大于400次谐波分解重构； 但是在25～30 keV处， 小波分解重构的谱信号存在弱噪声残留， 去燥效果稍弱于谐波分解。

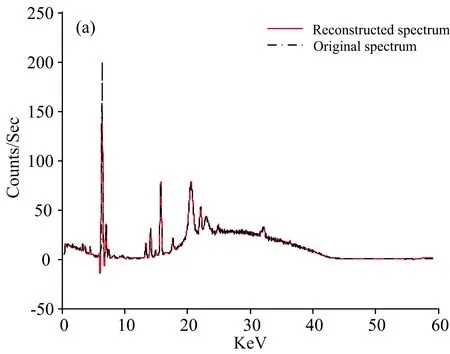
图10 土壤XRF光谱EMD(a)和小波分解(b)重构

综合分析以上三种方法， 从重构去噪效果来看， 采用400次HA分解重构处理土壤XRF光谱， 降噪效果理想， 小波分解重构次之， EMD降噪效果最差。 且400次HA分解重构耗时较短， 效能高， 因此， 谐波分解重构可作为土壤XRF光谱的有效去噪方法。

4.2 去噪XRF光谱的土壤Pb浓度超标检测

利用谐波分解重构方法对土壤XRF光谱进行降噪处理， 同时分析去噪XRF光谱的SPWVD， 总结发现， 该矿区周边土壤样品XRF光谱的SPWVD频率峰值主要集中分布在400， 600～700 cm-1波段序列上， 而400， 600～700 cm-1波段序列分别对应的荧光光谱波段为6.42和9.42～10.92 keV， 研究所得Pb浓度超标土壤的XRF光谱的SPWVD特征波段区间与前人研究结果较为接近[24]， 为快速识别相似地区土壤Pb浓度超标与否开拓了新思路。

5 结 论

采集内蒙古自治区锡林浩特市锡林郭勒盟某煤矿区周边的地表土壤， 利用Niton XL3t 950 PXRF光谱仪分析土壤XRF光谱及土壤Pb浓度， 研究该地区不同土壤样品频率域变换光谱与土壤Pb浓度超过当地土壤环境背景值(超标)之间的关系， 得到如下结论：

(1)详细分析了谐波分解重构法去除土壤XRF光谱的效能， 与EMD和小波分解方法所得结果进行对比， 发现当谐波分解次数为400次时， 光谱去燥效果较好并节省了时间， 且保留了光谱的特征。

(2)研究不同实地采样土壤样品去噪XRF光谱的SPWVD发现， 土壤样品Pb浓度与XRF光谱的SPWVD在400和600～700波段序列上的频率峰值的分布具有一定的规律性， 据此可识别该地区土壤的Pb浓度是否超标。 XRF光谱的SPWVD分布特征具体表现为： 在识别的75%Pb浓度不超标的土样中， 波段序列400附近有一个频率小于400 Hz的峰值或两个频率大于400 Hz的峰值； 在识别的79.17%的Pb浓度超标土样中， 波段序列400附近有一个频率大于400 Hz的峰值， 且在600～700波段序列之间有三个层次明显的频率峰值分布。 因此， 推断该地区土壤Pb浓度超标的XRF光谱特征波段区间为6.42和9.42～10.92 keV。