基于有限时间观测器的离散系统混沌同步

吴 阳，张建成

(1.无锡太湖学院机电工程学院，江苏无锡 214064;2.江南大学理学院信息与计算科学系，江苏无锡 214122)

1 引言

混沌系统是一类特殊的复杂非线性系统，具有非周期性、对初值敏感等不可预测性[1].混沌系统的这些不可预测性质使得它成为基于混沌同步-保密通信这一应用的重要载体.也因此，近几十年来许多学者对混沌同步不断展开研究，并取得了丰硕的成果.

对混沌同步的研究开始于20世纪90年代，时至今日已经有许多方法得到提出，如自适应同步法[2]、反馈控制法[3-4]、滑模控制法[5-6]、脉冲控制法[7]等.除了控制方法，基于观测器的混沌同步方法由于具有可靠性高、易于实现等特点，也不断见诸报道，并受到极大关注.例如，Pecora和Carroll将混沌系统看作驱动系统，通过构造混沌系统的状态观测器作为响应系统，提出了实现混沌同步的著名的“驱动-响应”模型[8-9].该模型的基本思想是，首先将混沌系统看作驱动系统，由它导出的输出作为驱动信号发送给信号接收端.随后，在信号接收端再由响应系统利用驱动信号将混沌系统的状态重构出来.基于这一经典模型，Nijmeijer等人对线性和非线性系统提出了多种基于观测器的混沌同步方法[10].Chen等人引入“等价输入注入”思想，通过构造滑模观测器同时实现了混沌同步和保密信号的还原[11].为了处理混沌系统非线性项，Chadli等人提出了T-S模糊未知输入观测器方法，进而将观测器的存在性问题转化成了线性矩阵不等式的可行解问题[12-13].Zhu等人在未知输入观测器匹配条件成立的条件下，设计自适应滑模观测器和降维观测器实现了混沌同步，并对全维和降维观测器方法的同步性能做了比较[14-15].而对于观测器匹配条件不成立的情形，Yang等人提出了利用高阶滑模微分器构造辅助输出的未知输入观测器混沌同步方法[16-18].近几年来，针对基于观测器的混沌同步方法的研究还被推广到分数阶系统中[19-20].

对于基于观测器的混沌同步来说，观测器的收敛精度和收敛速度是两个重要的指标.例如，在基于混沌同步的图像加密[18]中，响应系统在接收到驱动信号以后还必须在与驱动系统达到同步之后才能将加密信号还原出来.因此，准确而快速的混沌同步是加密信号能够高质量且及时地得到还原的重要保证.但是，目前报道出来的文献中基于渐近收敛观测器(asymptotic convergence observer，ACO)的混沌同步方法大都仅能实现响应系统状态对驱动系统状态的渐近跟踪[10-20].对于渐近收敛观测器来说，它的优点是设计方法简单，并且对系统本身要求不高.但是，渐近收敛观测器的收敛速度和收敛精度往往很难得到控制.这是因为渐近收敛观测器的收敛效果不仅依赖于原系统和观测器系统的状态初始误差，同时还依赖于观测器的极点配置.由于系统初值很难获得，作者很难通过对观测器初始条件的设置来减小初始误差、提高收敛效果.一个可选的方案是对观测器系统选取尽可能大的增益矩阵使得系统极点远离虚轴.但这样的做法一方面只能在一定程度改善观测器的收敛精度和速度(仍然不能控制观测器的收敛时间和精度)，另一方面，大增益矩阵的引入可能会使得观测器系统对噪声更为敏感从而降低观测器的估计性能.所以，对于基于ACO的混沌同步来说，无论是精度还是速度在一个较短的时间内往往都得不到很好地保证.因此，针对混沌同步提出一种估计精度高且收敛速度快的有限时间观测器方法很有意义.值得注意的是，近年来已经有文献对有限时间混沌同步问题展开研究.例如，借助于超螺旋算法(super twist algorithm)文献[21]讨论了基于混沌同步的保密通信问题.由于超螺旋算法本身具有有限时间收敛性质，该同步可以在有限时间内完成，但该方法只能保证同步误差保持有界.此外，基于有限时间稳定性理论，文献[22-23]分别研究了混沌系统的全局有限时间同步[15].但是，无论是文献[22]还是文献[23]其同步时间都依赖于主从系统的状态初值而不能根据实际需要提前设定.

针对以上所述问题，本文对一类离散时间混沌系统提出一种基于有限时间观测器(finite-time observer，FTO)的混沌同步方法以克服传统渐近收敛观测器和有限时间观测器方法存在的缺点和不足.本文的主要贡献和创新之处体现在:1)给出了可实现混沌系统有限时间精确同步观测器设计的充分条件;2)给出了离散时间有限时间观测器的结构;3)将构造的有限时间观测器应用到混沌同步中，该观测器可以在任意预先设定的时间内实现响应系统对驱动系统的精确同步，可以同时满足对收敛速度和收敛精度的需求，且这些性能不会受到初始条件的影响.

本文余下部分安排如下:第2节为问题背景和预备知识;第3节给出有限时间混沌同步观测器的构造;第4节对两个离散混沌系统例子进行仿真模拟;最后，在第5节中给出本文的结论.

2 问题背景和问题描述

考虑如下离散混沌系统作为驱动系统的同步问题:

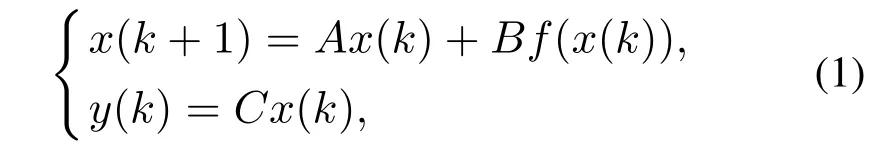
其中:x ∈ℝn，y ∈ℝp分别为驱动系统的状态向量和输出(驱动信号)向量;f(·):ℝn→ℝq为混沌系统的非线性项;A，B，C分别为具有适当维数的常数矩阵(n ＞p ≥q)且矩阵B，C 均为满秩矩阵.

事实上，很多离散混沌系统都可以用式(1)来表示.例如，著名的Henon映射[24]

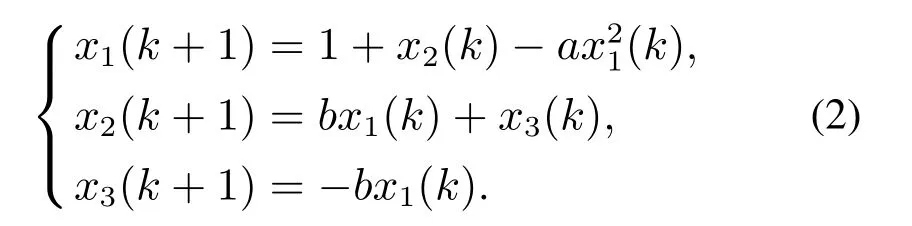
当a=1.08，b=0.3且x1(0)=x2(0)=x3(0)=1时就是一个典型的混沌系统.显然，系统(2)可以由式(1)来表示，其相应的系统矩阵和参数为

为了利用未知输入观测器理论设计有限时间观测器作为响应系统实现状态同步，将非线性函数f(x(k))看作未知信号来处理.本文给出以下两个重要的假设条件.

假设1系统(1)(或者表示为Σ(A，B，C))满足观测器匹配条件[25]，即

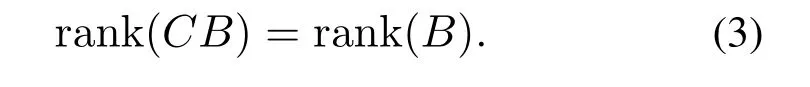
假设2系统(1)(或者表示为Σ(A，B，C))满足强可观条件[25]，即对于任意复数s都有

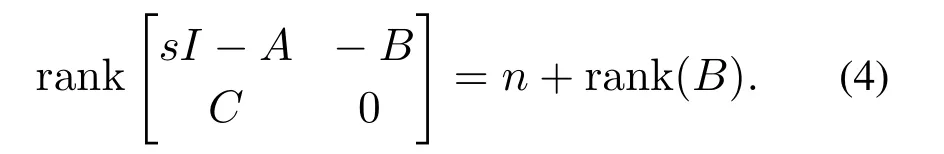
注1在经典的未知输入观测器设计中，观测器匹配条件是一个基本条件，它用来解耦掉未知输入对观测器设计的影响.而强可观条件则可以保证观测器系统极点可以得到任意配置.

3 有限时间同步观测器设计

受文献[26]中连续时间线性时不变系统有限时间观测器设计思路的启发，本节考虑带有未知输入的离散系统有限时间观测器设计问题，并将其应用于混沌同步.

由于rank(B)=q ＜n，因此可以找到一个矩阵U ∈ℝn×(n-q)使得T=[B U]为非奇异.对于系统(1)的状态方程，实施状态变换得

4 数值模拟

本节给出两个混沌系统的例子来验证所提方法的有效性.

4.1 仿真算例1

考虑本文第2节给出的Henon系统(2)[24].容易验证，Σ(A，B，C)同时满足假设1-2，因此可以设计有限时间观测器作为响应系统在任意短时间步内和系统(2)的状态达到同步.根据算法1，取矩阵

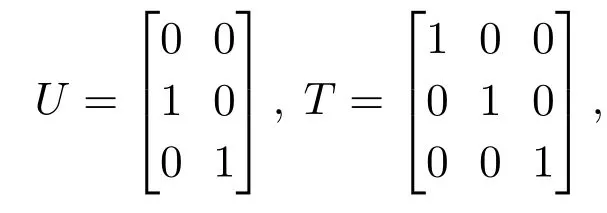
进而求得

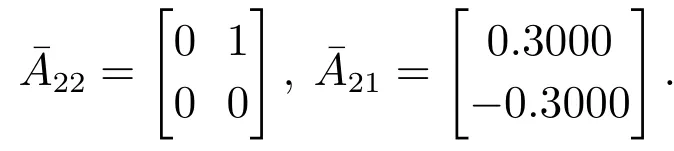
更进一步地，取H=[0 1]T，则相应地，可求出V1=[0 1]和V2=[1 0].然后，取增益矩阵

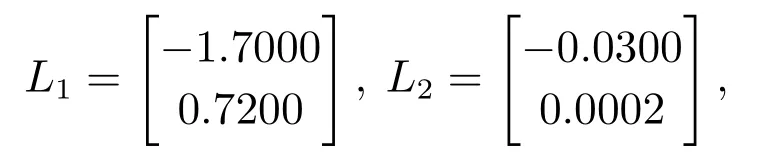
使得矩阵

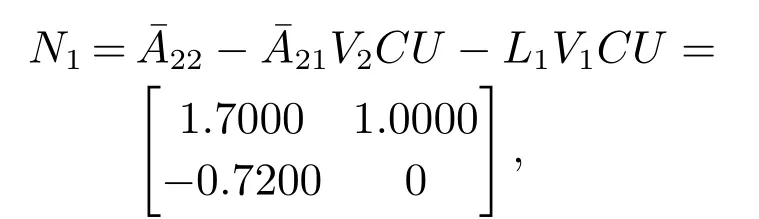
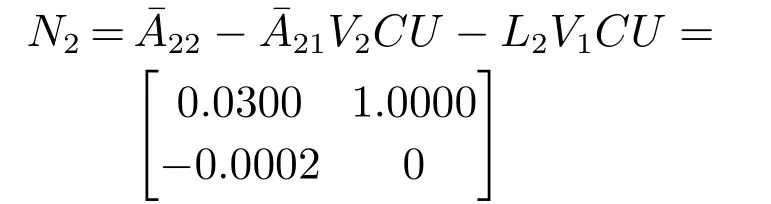
的特征值分别为{0.9，0.8}和{0.02，0.01}

为了验证观测器的有限时间收敛性，这里不妨假设收敛时间步长k0=2，那么相应的增益矩阵K 为

为了验证算法的有效性，在系统(2)中取初值x(0)=[1 1 1]T.图1显示该系统具有混沌特性.对于响应系统(有限时间观测器)，取初值

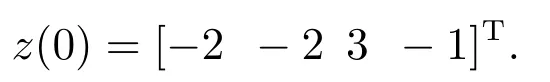
借助于MATLAB软件将仿真结果绘于图2.图2中曲线分别表示混沌状态曲线、基于FTO的同步曲线和基于ACO的同步曲线.可以发现，在预先设定的k0=2时刻，基于FTO方法的同步曲线和驱动系统状态曲线即可达到精确同步.而传统的基于ACO的方法达到同步的时间要k ≥50.因此，本文提出的基于有限时间观测器的混沌同步方法在同步速度上远高于传统方法.

基于有限时间观测器的混沌同步还有一个显著特点:混沌同步的精确程度和达到同步所需要的时间步长均不依赖于观测器的初值.为了说明该特点，本文分别选取观测器初值为

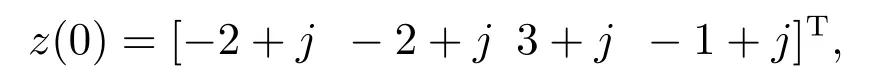
其中j分别取为－2，－1，0，1，2.图3展示了在观测器分别选定不同初值情况下的混沌同步性能.从图中可知，无论观测器初值如何选取，在预先设定的时间步长k=k0内响应系统都可以精确地同步混沌系统.

此外，为了验证本文方法对具有不确定干扰的混沌系统同样适用，假设系统(2)为

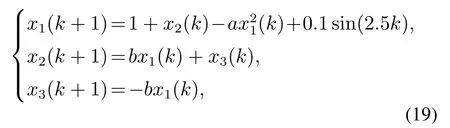
4.2 仿真算例2

考虑如下的三阶超混沌系统[24]:

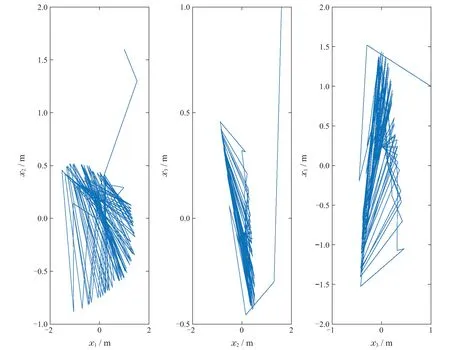
图1 Henon混沌系统的状态轨迹Fig.1 Trajectory of the Henon chaotic system

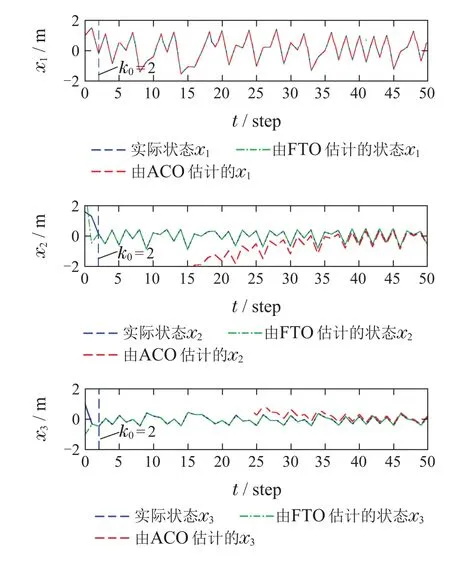
图2 基于FTO和ACO的混沌同步效果(不含干扰)Fig.2 FTO and ACO-based chaotic synchronization performance(without disturbance)

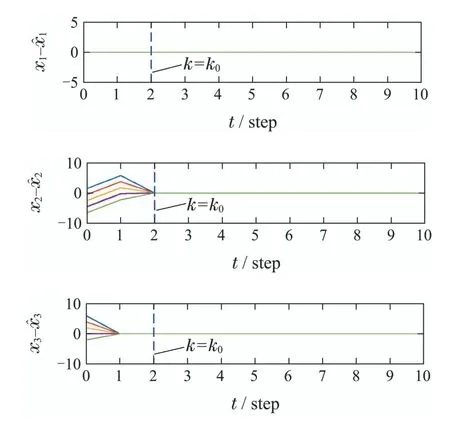
图3 观测器取不同初值时的混沌同步效果Fig.3 Chaotic synchronization performance with different observer initial values

如图5，当参数取值为a1=1.7，a2=0.05 时系统(20)表现出混沌特性.假设系统输出为y1(k)=x1(k)，y2(k)=x3(k)，并 记，则可以将系统(20)写为系统(1)的形式，其参数为

容易验证，该系统同时满足强可观条件和观测器匹配条件，故本文提出的有限时间观测器FTO存在.根据算法1计算出如下矩阵:

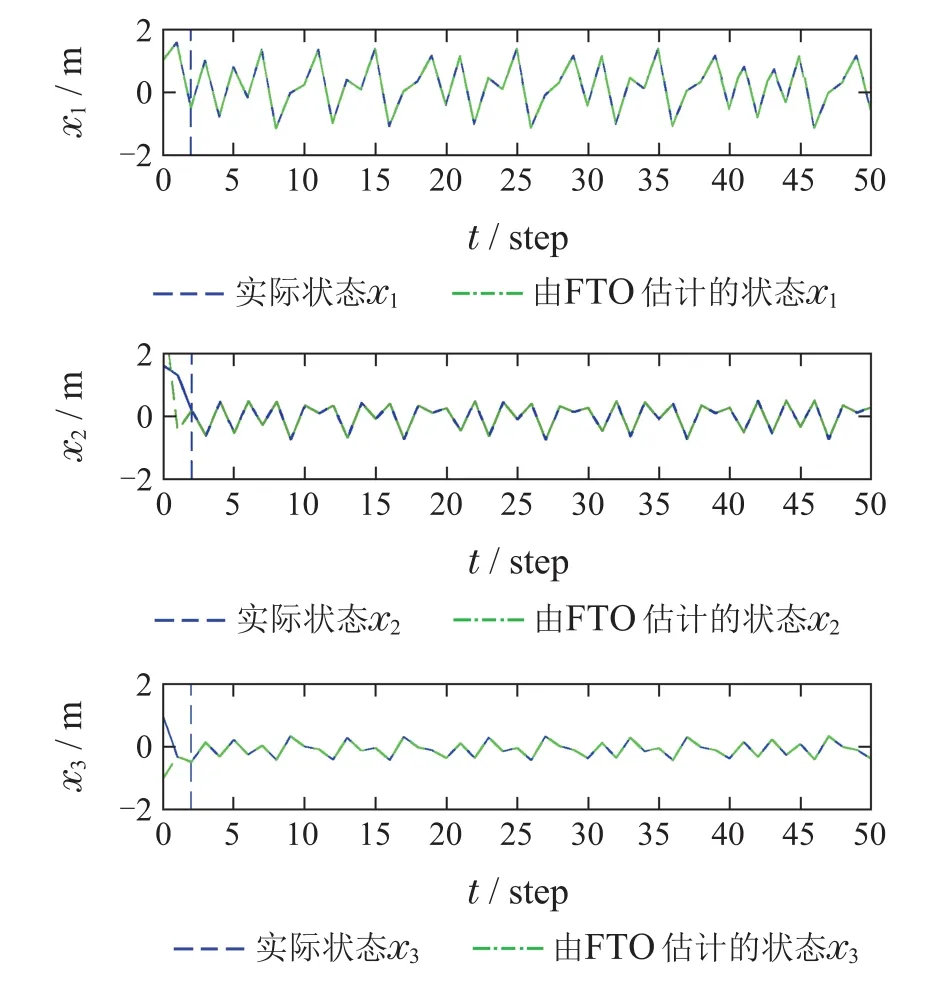
图4 基于FTO和ACO的混沌同步效果(含干扰)Fig.4 FTO and ACO-based chaotic synchronization performance(with disturbance)

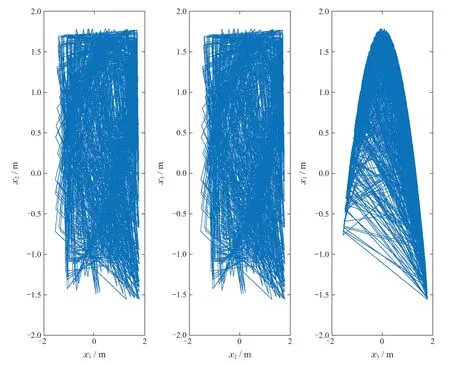
图5 混沌系统(20)的状态轨迹Fig.5 Trajectory of chaotic system(20)

基于以上参数矩阵，建立有限时间观测器(10)-(12).同样地，在本例中为了将本文所提方法与传统方法作比较，将混沌系统(20)的真实状态曲线、基于FTO的同步曲线和基于传统ACO方法的同步曲线绘于图6中.从图6可知，利用FTO的同步方法可以在k0=2步时迅速达到同步，而利用传统的ACO方法则需要耗时大约40步才能达到同步.因此，本文所提方法在同步速度上具有明显优势.

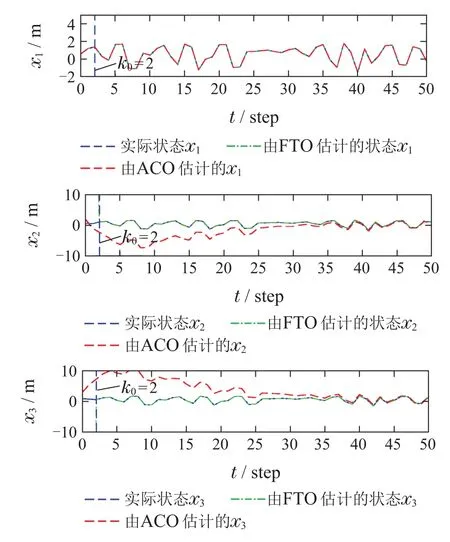
图6 基于FTO和ACO的混沌同步效果Fig.6 FTO and ACO-based chaotic synchronization performance

基于FTO方法的另一优势在于可以对同步时间k0根据需要预先任意设定.为了验证这一点，随意选取k0=2，3，5，10，其中FTO的初值取为

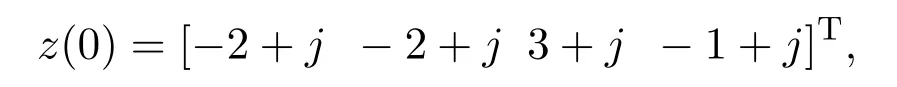
其中j=－2，－1，0，1，2.

图7-10分别展示了k0取不同值时观测器误差收敛到0的情形.

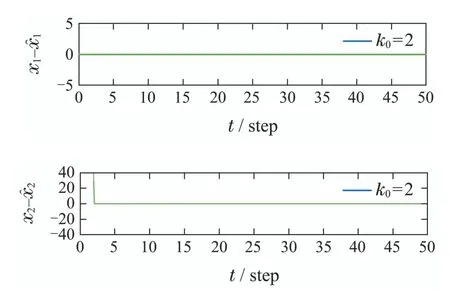
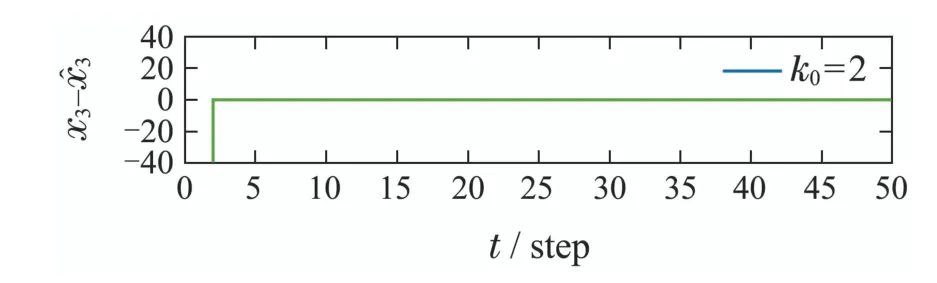
图7 观测器取不同初值时的混沌同步效果(k0=2)Fig.7 Chaotic synchronization performance with different observer initial values(k0=2)

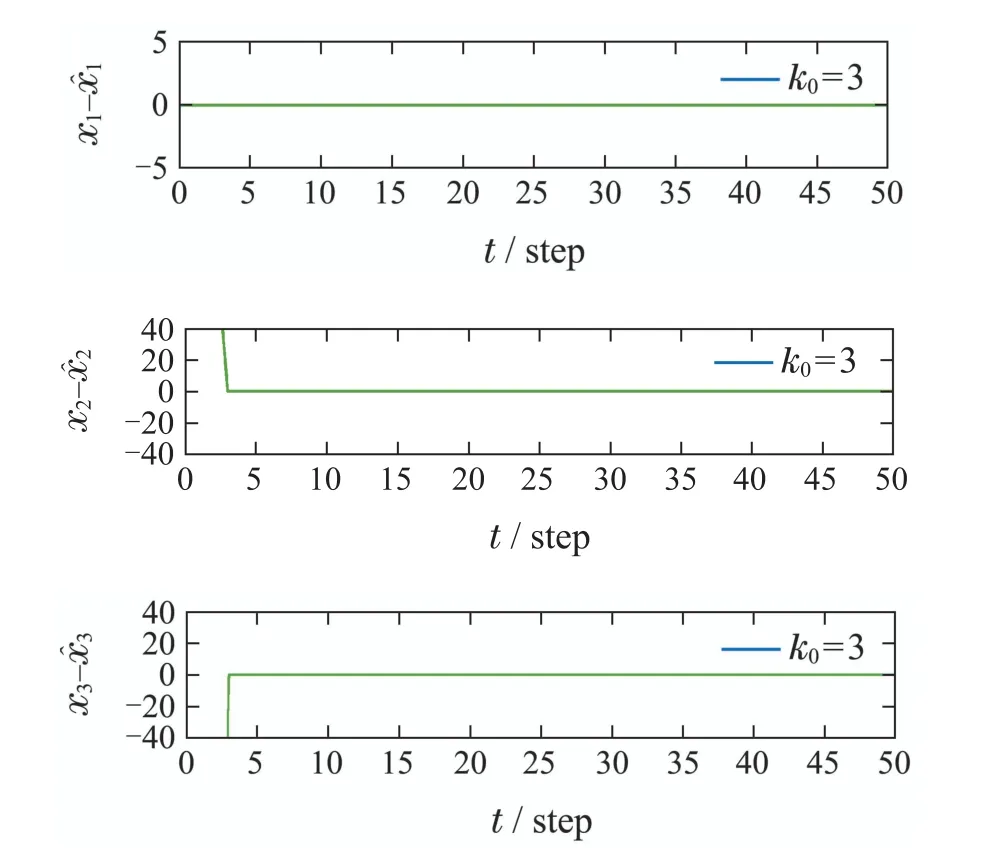
图8 观测器取不同初值时的混沌同步效果(k0=3)Fig.8 Chaotic synchronization performance with different observer initial values(k0=3)

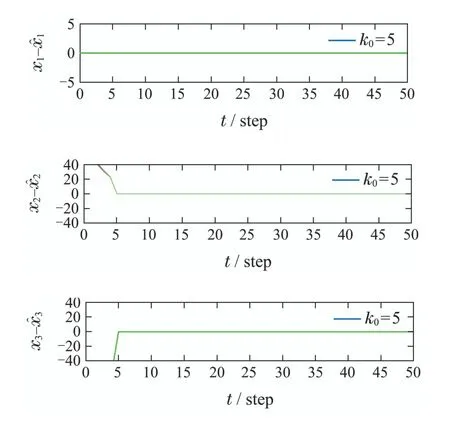
图9 观测器取不同初值时的混沌同步效果(k0=5)Fig.9 Chaotic synchronization performance with different observer initial values(k0=5)

从图7-10中可知，无论k0取为何值，在预先设定的k0步内，本文所提出的FTO方法均可以达到对混沌系统的精确同步.

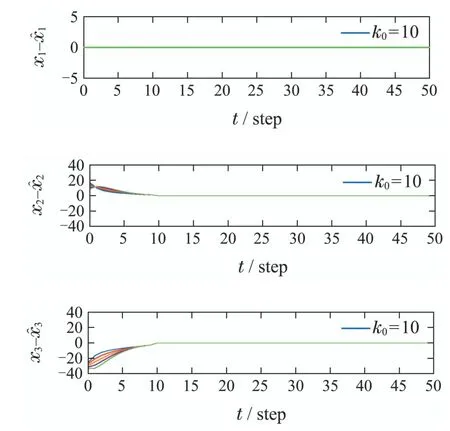
图10 观测器取不同初值时的混沌同步效果(k0=10)Fig.10 Chaotic synchronization performance with different observer initial values(k0=10)

5 结论

本文针对离散时间混沌系统提出了一种基于有限时间观测器的混沌同步方法.相比于传统的基于渐近收敛观测器的混沌同步方法，本方法同步程度更加精准，达到同步所需时间可以任意设定.因此，本方法能够同时保证混沌同步的效果和速度.但是，也需要指出本文方法所要求的强可观条件保守性较高，如何降低该条件给有限时间观测器设计带来的保守性是一项有意义的课题，值得进一步研究.此外，如何将线性系统有限时间观测器方法推广到线性参数变化(linear parameter-varying，LPV)系统也是下一步要考虑的课题.