考虑误差补偿的柔性关节机械臂命令滤波反步控制

李鹏飞，张银河，张 蕾 ，王晓华，王文杰

(1.西安工程大学电子信息学院，陕西西安 710048;2.西安工程大学陕西省2011产业用纺织品协同创新中心，陕西西安 710048)

1 引言

柔性关节机械臂因质量轻、耗能少、惯性小、高适应性，可进行安全的人机交互等优点，在航空航天、柔性制造、纺织服装、医疗、康复等行业拥有巨大的应用前景和发展潜力[1-3].然而由于关节柔性的增加，柔性关节机械臂在运动过程中易产生振动，使力和位置的控制精度降低，直接影响到机器人的响应速度和控制精度等运行指标.

针对以上问题，研究者们提出了多种控制策略用于柔性关节机械臂的控制，其中最常用的控制方法是比例微分(proportional-derivative，PD)加重力补偿[4-5]，但是这种控制方法只适合状态反馈位置控制，对于轨迹跟踪控制来说，其性能会极大降低.为克服PD控制的局限性，研究者们又采用了奇异摄动控制[6-7]、反步控制[8-10]、自适应控制[11-12]、变结构控制[13-14]、智能控制[15-18]等非线性控制策略来提高柔性关节机械臂的控制精度.当进行接触性控制任务时，需要柔性关节机械臂具有柔顺性，研究者们也提出了基于控制算法的主动柔顺控制方法和基于安装在机械臂末端关节的被动柔性装置的被动柔顺控制方法[19-22].本文针对柔性关节机械臂的轨迹跟踪控制策略进行研究.

为了获得良好的控制性能，在设计柔性关节机械臂控制器时，一方面，需要考虑到其动力学模型非线性、强耦合、参数时变的特点;另一方面，对于实际的柔性关节机械臂控制系统，还必须考虑反馈系统的实际限制，例如:执行器的结构和参数存在不确定性、信号延迟和未建模的动态、重复性运动时，易受到周期性的干扰等不确定性问题[9].反步法因其能够有效地消除参数时变和外界扰动对系统性能的影响，在柔性关节机械臂的控制中具有显著的优势[23].文献[24]提出了一种模糊自适应反步控制方法用于人体上肢外骨骼康复机器人，该方法结合了外骨骼的迭代学习控制来提供前臂运动的辅助，使人的前臂能够在结构和参数不确定、存在未建模动力学和环境扰动的情况下跟踪任何连续的期望轨迹(或设定的恒定点).然而，该方法需要对虚拟控制函数反复求偏导，从而导致“计算爆炸”的问题.文献[25]提出了一种柔性关节机械臂自适应动态面控制方法，该方法将反步过程中设计的虚拟控制函数经过一阶低通滤波器，得到滤波后的虚拟控制函数，再经过一阶低通滤波器得到滤波后虚拟控制函数的导数，以消除“计算爆炸”问题，但该方法没有考虑到采用滤波器引起的滤波误差对系统的控制性能的影响.

本文提出一种用于柔性关节机械臂的具有误差补偿机制的命令滤波反步控制(command-filtered backstepping control，CFBC)方法.该方法将所设计的虚拟控制函数经过二阶命令滤波器来得到滤波后的虚拟控制函数及其导数，避免了对虚拟控制函数的多阶求导所导致的计算爆炸问题，同时引入了滤波误差补偿机制，并通过李雅普诺夫稳定性理论证明了该误差闭环系统的稳定性.最后，通过MATLAB仿真来证明所提出方法在柔性关节机械臂轨迹跟踪控制中的有效性.

2 柔性关节机械臂数学建模和控制目标

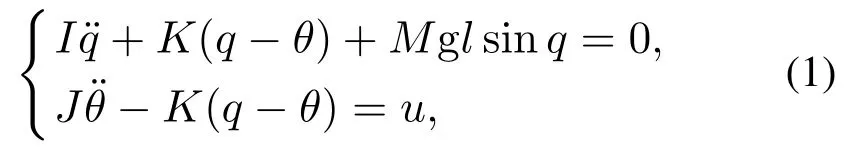
本文针对单连杆柔性关节机械臂进行控制策略研究，首先，建立单连杆柔性关节机械臂动力学模型如下[26]:{其中:q，θ分别表示关节位置和电机的转角位置，I，J分别表示关节的转动惯量和电机的转动惯量，M，g，l分别表示关节质量、重力加速度、关节到杆质心距离，K表示关节刚度系数，u是电机转矩输入.

由于使用二阶命令滤波器得到反步法中所需的虚拟控制函数及其导数过程中，会产生滤波误差，本文提出一种改进的命令滤波反步控制方法，希望通过引入滤波误差补偿机制，来提高关节角度跟踪期望角度的精度，根据这一控制目标，选取系统中的q，θ作为状态变量，并将式(1)整理为以下非线性系统形式:

假设1g1，g2为已知常数，f1，f2为具体形式的连续未知函数，其一阶导数连续有界.

假设2理想轨迹qd连续、有界，其一阶导数和二阶导数连续、有界.

引理1本文采用的二阶命令滤波器定义如下[27]:

引理2 针对[28]:V :[0，+∞)∈ℝ，不等式方程，∀t ≥t0≥0的解为

其中a为任意常数.

本研究的控制目标可总结为:为系统(1)设计一种非线性的轨迹跟踪控制策略，以确保柔性关节机械臂的关节位置q跟踪期望轨迹qd，跟踪误差q－qd可收敛到零附近的一个邻域内，即∀β ＞0，∃t0≥0，当t ＞t0时，有|q－qd|＜β，并且闭环系统的所有状态变量连续稳定有界.

3 柔性关节机械臂命令滤波反步控制器(CFBC)设计

根据控制目标中的轨迹跟踪任务，定义如下跟踪误差:

由于使用命令滤波器会产生滤波误差，影响系统性能，本文通过引入误差补偿机制来减少滤波误差，因此，选取误差补偿信号为

其中:αi(i=1，2，3)为虚拟控制函数，为经过滤波器后的虚拟控制函数，ki(i=1，2，3)为所设计的大于0 的常数，δi(0)=0(i=1，2，3，4)为初始值.由文献[29]可知，滤波误差补偿信号δi(i=1，2，3，4)满足

其中:k0=min(k1，k2，k3，k4)，ρ为正常数，定义虚拟控制函数的滤波误差为

从而建立补偿后的跟踪误差子系统如下式所示:

根据前述控制目标，在后续的设计中将通过命令滤波反步算法来保证r1，r2，r3，r4尽可能小，同时保证闭环系统所有状态变量连续稳定有界.控制系统框图如图1所示，具体步骤将在下面的设计中给出.

图1 控制系统框图Fig.1 Block diagram of the control system

步骤1对上述定义的第1个补偿后的跟踪误差r1求导可得

选取第1 个误差子系统的Lyapunov 函数为V1=，对其求导得

将α1视为该子系统的虚拟控制输入，设计虚拟控制函数为

其中k1＞0为常数.将式(6)(10)代入式(9)得

由上式可知，当r2=0时，.但在这一步骤中不能保证r2总是为0.为此，需要在下一步骤设计时，引进虚拟控制函数α2，使第1个误差子系统闭环稳定.

步骤2对上述定义的第2个补偿后的跟踪误差求导可得

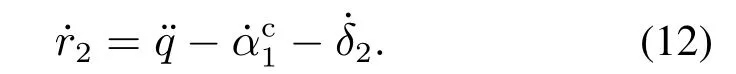
选取第2个误差子系统的Lyapunov函数为

其中I为关节的转动惯量，对其求导得

将α2视为该子系统的虚拟控制输入，设计虚拟控制函数为

其中k2＞0为常数.将式(1)(6)和式(14)代入式(13)得

由上式可知，当r3=0时，.但这一步骤中不能保证r3总是为0.为此，需要在下一步骤设计时，引进虚拟控制函数α3，使第2个误差子系统闭环稳定.

步骤3对上述定义的第3个补偿后的跟踪误差求导可得

选取第3个误差子系统的Lyapunov函数为

对其求导得

将α3视为该子系统的虚拟控制输入，设计虚拟控制函数为

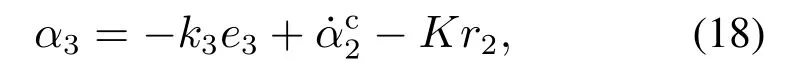
其中k3＞0为常数，将式(6)(18)代入式(17)得

由上式可知，当r4=0时，.但这一步骤中不能保证r4总是为0.为此，需要在下一步骤设计时，通过设计系统的真实控制函数τ，使第3个误差子系统闭环稳定.

步骤4对上述定义的第4个补偿后的跟踪误差求导可得

选取第4个误差子系统的Lyapunov函数为

其中J为电机的转动惯量，对其求导得

在这一步中，出现了系统的真实控制输入u，τ即为该子系统的真实控制函数，取最终控制函数为

其中k4＞0为常数.将式(1)(22)代入式(21)得

4 稳定性证明

选取整个补偿后的误差闭环系统(7)的Lyapunov函数为

由式(23)可得

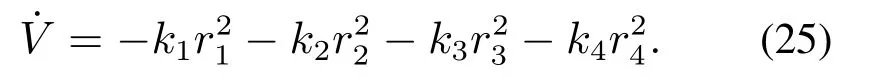
将式(24)代入式(25)可得

采用引理2，针对式(26)可得

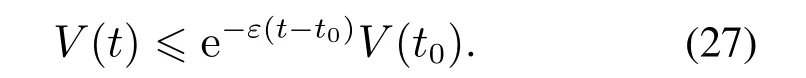
由式(27)可得，当t →∞时，V(t)指数收敛至零，收敛速度取决于ε.又由式(24)可得，当t →∞时，r1→0，r2→0，r3→0，r4→0.由式(7)可得

由引理1和k0的定义可得，从理论上分析，通过调节命令滤波器参数ωn和ζ，以及调节系统参数k1，k2，k3，k4就可以保证轨迹跟踪误差e1收敛到零附近的一个邻域内.

综上所述，根据假设1和假设2可得，该闭环系统所有状态变量是连续稳定有界，系统跟踪误差e1最终收敛到零附近的一个邻域内.

5 实验验证

为了验证本文所提出方法的有效性，在MATLAB/Simulink环境下对单关节柔性机械臂控制系统进行了仿真研究.系统的参数选定如下:

仿真中设定关节位置q 跟踪的理想轨迹为qd=sin t.仿真结果见图2-12所示.

图2为本文所提出的方法在控制器参数k1=5，k2=60，k3=30，k4=5，ζ=0.5 条件下，改变ωn的值，关节轨迹跟踪误差e1响应曲线.

图2 在参数k1=5，k2=60，k3=30，k4=5，ζ=0.5下本文所提方法的关节轨迹跟踪误差e1响应曲线Fig.2 The tracking error of the joint using the proposed control method with parameters k1=5，k2=60，k3=30，k4=5，ζ=0.5

图3为本文所提出的方法控制器参数ζ=0.5，ωn=250条件下，改变k1，k2，k3，k4的值，关节轨迹跟踪误差e1响应曲线.

图3 在参数ζ=0.5，ωn=250下本文所提方法的关节轨迹跟踪误差e1响应曲线Fig.3 The tracking error of the joint using the proposed control method with parameters ζ=0.5，ωn=250

由图2可见，二阶命令滤波器参数ζ=0.5，通过增加ωn的值，关节轨迹q跟踪理想轨迹qd的误差e1随之减小，这证明了命令滤波器的参数ωn直接影响到系统的跟踪误差e1.由图3可见，通过增加k1，k2，k3，k4的值，关节轨迹q跟踪理想轨迹qd的误差e1随之减小，即实验结果与上述第4部分得到的结论相对应.

图4-6分别是本文所提CFBC方法，反步方法和常规PD加重力补偿方法[4]作用在柔性关节机械臂上，其关节轨迹q跟踪理想轨迹qd的响应曲线和跟踪误差e1响应曲线.

图4 本文所提方法的关节位置跟踪响应曲线和跟踪误差e1响应曲线Fig.4 The position tracking and tracking error of the joint using the proposed control method

图5 反步方法关节位置跟踪响应曲线和跟踪误差e1响应曲线Fig.5 The position tracking and tracking error of the joint using the backstepping control method

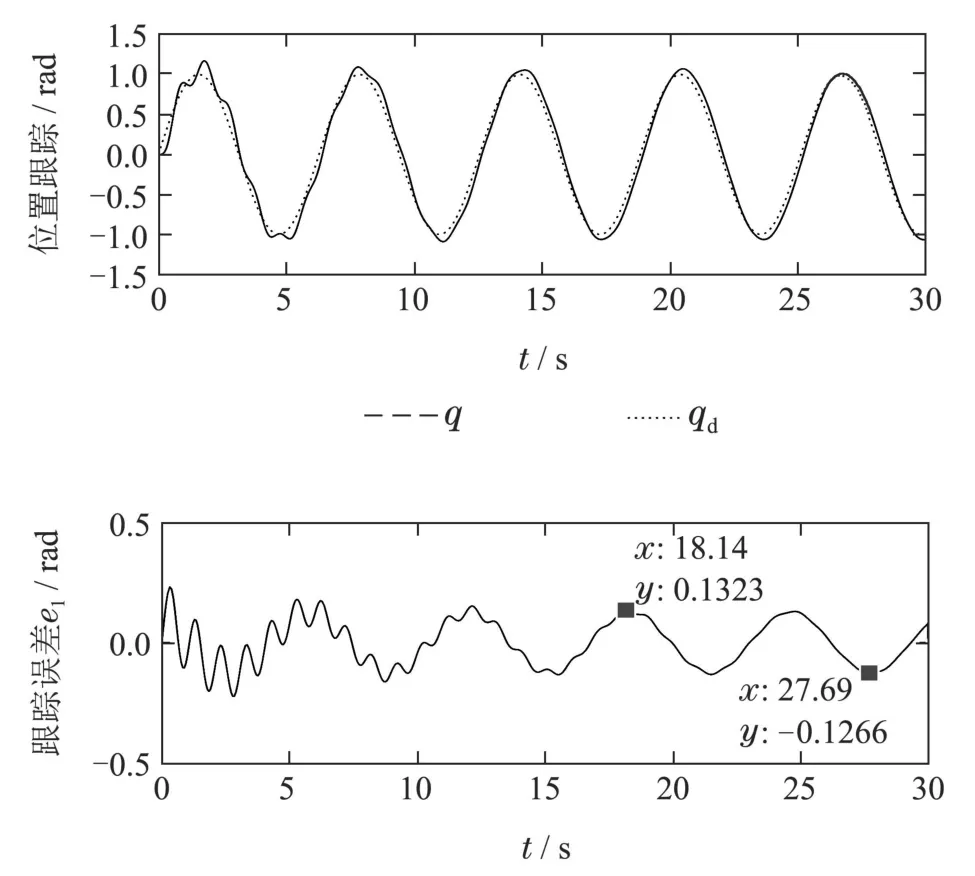
图6 PD加重力补偿方法关节位置跟踪响应曲线和跟踪误差e1响应曲线Fig.6 The position tracking and tracking error of the joint using the PD control with gravity compensation control method

由图可见，图4 为控制器参数k1=5，k2=60，k3=30，k4=5，ζ=0.5，ωn=250 条件下，本文所提CFBC 方法的关节位置跟踪响应曲线和跟踪误差e1响应曲线，波形稳定后跟踪误差e1在[－0.0008477，0.0008481]之间.图5为未采用命令滤波器，相同控制器参数k1=5，k2=60，k3=30，k4=5 条件下，反步控制方法的关节位置跟踪响应曲线和跟踪误差e1响应曲线，波形稳定后跟踪误差e1在[－0.05826，0.0821]之间.图6 为kp=400，kd=40条件下，PD加重力补偿控制方法的关节位置跟踪响应曲线和跟踪误差e1响应曲线，波形稳定后跟踪误差e1在[－0.1266，0.1323]之间.综合图4－6可见，波形稳定后，本文提出的考虑误差补偿的命令滤波反步控制方法(CFBC)的控制精度最高，PD加重力补偿控制方法控制精度最低，反步控制方法的控制精度在两者之间.

为了进一步说明本文所提CFBC方法在柔性关节机械臂的关节位置轨迹跟踪方面的优势，将未考虑误差补偿的命令滤波反步方法关节位置跟踪响应特性进行仿真，图7为与图4相同控制器参数条件下，未考虑误差补偿的命令滤波反步方法的关节轨迹q跟踪理想轨迹qd的响应曲线和跟踪误差e1响应曲线.

由图7可见，波形稳定后跟踪误差e1在[－0.0009727，0.0009725]之间.对比图4 和图7 可得，在仿真实验所设定的参数条件下，考虑滤波误差补偿，控制器的精度最大可以提高12.7%.

图7 未考虑误差补偿的命令滤波反步方法的关节位置跟踪响应曲线和跟踪误差e1响应曲线Fig.7 The position tracking and tracking error of the joint using the command-filtered backstepping control method without error compensation

接下来分析在本文所提CFBC方法中所设计的虚拟控制函数的滤波误差的动态响应特性.图8为考虑滤波误差补偿和未考虑滤波误差补偿条件下，虚拟控制函数α1的滤波误差响应曲线.图9为考虑滤波误差补偿和未考虑滤波误差补偿条件下，虚拟控制函数α2的滤波误差响应曲线.图10为考虑滤波误差补偿和未考虑滤波误差补偿条件下，虚拟控制函数α3的滤波误差响应曲线.控制器参数为

图8 命令滤波反步方法的虚拟控制函数α1滤波跟踪误差响应曲线Fig.8 The filtering tracking error of the virtual control function α1 use the command-filtered backstepping control method

图9 命令滤波反步方法的虚拟控制函数α2滤波跟踪误差响应曲线Fig.9 The filtering tracking error of the virtual control function α2 use the command-filtered backstepping control method

图10 命令滤波反步方法的虚拟控制函数α3滤波跟踪误差响应曲线Fig.10 The filtering tracking error of the virtual control function α3 use the command-filtered backstepping control method

综合图8－10可见，本文所提方法所得到的虚拟控制函数αi(i=1，2，3)的滤波误差比未考虑误差补偿情况下明显减少.

最后，分析本文所提CFBC方法在控制律响应速度方面的特性.图11为未考虑误差补偿的命令滤波反步方法力矩输入曲线，图12为本文所提出方法的力矩输入曲线.控制器参数为

对比图11和图12可以看出，当考虑滤波误差补偿时，力矩输入曲线更快趋于稳定，比不考虑滤波误差补偿时进入稳态时间缩短了约0.06 s.证明了本文所提方法虽然加入了滤波误差补偿信号，但并未影响到控制系统的响应速度.

图11 未考虑误差补偿的命令滤波反步方法力矩输入曲线Fig.11 The control torques input using the command-filtered backstepping control method without error compensation

图12 本文所提方法的力矩输入曲线Fig.12 The control torques input using the proposed control method

综合以上仿真结果可以看出:本文所提出的CFBC方法与常规柔性关节机械臂关节轨迹跟踪控制所用的PD加重力补偿方法和传统反步方法相比较，柔性关节机械臂控制精度有明显提高，与未考虑滤波误差补偿的命令滤波反步方法相比较，柔性关节机械臂的控制精度更高，暂态响应效果更好.

6 结论

本文将命令滤波反步方法用于柔性关节机械臂轨迹跟踪控制，通过引入滤波误差补偿机制，来消除滤波误差对控制性能的影响，并且根据Lyapunov稳定性理论分析了系统的稳定性，最后通过MATLAB对比实验验证了所提出方法的有效性.实验结果如下:1)通过调节命令滤波器参数ωn和ζ，以及调节系统参数k1，k2，k3，k4，对比所得到的跟踪误差e1的响应曲线，证明了论文第4部分的结论;2)通过对比本文所提出的CFBC方法与反步方法，常规PD加重力补偿方法的跟踪误差e1的响应曲线，证明了本文所提方法可实现最高的跟踪精度;3)通过对比本文所提出的考虑误差补偿的CFBC方法与未考虑误差补偿的CFBC方法的跟踪误差e1的响应曲线、虚拟控制函数αi(i=1，2，3)的滤波误差响应曲线、力矩输入曲线，证明了本文所提出的CFBC方法跟踪精度更高，滤波误差明显减少，力矩输入曲线更快趋于稳定.

本研究对于拓展反步法在柔性关节机械臂的应用具有重要意义，但本文所提出的CFBC方法仅考虑了在单关节柔性机械臂的应用，对于多关节机械臂的应用效果尚不可知，后期将考虑扩展到多关节柔性机械臂的应用，并且考虑引入自适应鲁棒控制方法以克服柔性关节机械臂动力学模型存在的参数不确定特性和未知的外界干扰影响系统暂态性能的问题.