GNSS导航星座近实时精密轨道解算方法研究

肖长伟，曲国鹏，闫高原，刘家兴

（江苏建筑职业技术学院建筑工业化与信息化应用技术研究所，江苏 徐州 221116）

1 引言

在GNSS系统中导航星座近实时精密轨道是保障系统正常运行的关键技术之一。GNSS导航星座近实时轨道精度是衡量GNSS卫星导航系统性能的一个重要指标[1-2]。GNSS导航星座的近实时精密轨道是保障GNSS精密定位、导航以及低轨卫星精密定轨的基础，因此，GNSS导航星座近实时精密轨道解算技术一直受到国内外许多专家和研究机构的重视，成为全球导航定位系统领域重要的研究课题[3-5]。

随着全球导航定位技术应用深入，社会对全球导航系统实时性和高精度的需求不断增加，迫切需要基于GNSS导航星座实时精密轨道的高精度实时定位服务，研究GNSS导航星座高精度实时定位服务系统将有利于促进GNSS导航星座定位、定轨理论和算法的发展。GNSS导航星座近实时精密轨道确定技术作为实现GNSS高精度实时定位导航服务的核心技术，已经成为全球卫星导航定位领域最热门研究课题之一[2]。

为了提高我国在政治、经济和军事领域的世界地位，我国正在大力建设完全具有自主知识产权的全球卫星导航系统——中国北斗卫星导航系统，北斗卫星导航系统由空间段、地面段和用户段3部分组成，可以在全球范围内全天候、全天时为世界范围内各类用户提供高精度，稳定可靠的定位、导航和授时服务，并具有其他全球卫星导航系统没有的全球通信功能。从2007年4月第一颗北斗导航卫星的成功发射到今天为止我国已经成功发射了45颗北斗导航卫星，我国北斗卫星导航系统已基本建设成熟。但是，由于我国北斗卫星导航系统跟踪站的布设主要设置在国内，卫星跟踪弧段有限，因此，跟踪网的基准约束条件和几何观测结构都相对比较弱，导致我国北斗卫星导航星座的轨道精度以及轨道解算的实时性相对较差，因此，怎样进行近实时导航星座精密轨道确定成为了重要的研究课题[6-7]。

文章利用滑动数据窗口内短弧法方程叠加的方法，基于2018年年积日为89天～91天全球均匀分布的60个IGS站的观测数据，解算GNSS导航星座近实时精密轨道数据，然后与CODE提供的精密轨道作比较，评价滑动数据窗口内短弧法方程叠加方法解算的近实时轨道可靠性和精度[6-7]。

2 GNSS导航星座近实时轨道解算

2.1 GNSS导航星座近实时轨道解算流程

图1 导航星座近实时轨道解算流程图

图1为GNSS导航星座近实时轨道的解算流程图，以全球均匀分布的60个IGS站提供的6h的观测数据生成一个短弧段法方程，滑动窗口为2d48h的观测数据（共8个6h短弧段法方程）。短弧段法方程进程处理当前6h时间段上可获得的实时观测数据，数据解算结束后生成包括卫星初始状态、地球自转参数、力模型参数、测站坐标、大气参数和模糊度参数等的6h短弧段法方程，在当前的6h短弧段法方程生成之后，利用短弧法方程叠加的方法与前七个6h短弧段法方程（共8个6h短弧段法方程）合并成一个法方程，求解出由整个滑动窗口中48h数据求出的卫星初始轨道和力模型参数，然后利用轨道积分的方法得到2d48h的轨道以及预报以后6h的轨道，其中，我们把预报的6h的轨道作为近实时精密轨道。其后，将下一个6h短弧段法方程与相对于下一个6h短弧段法方程之前的7个6h短弧段法方程合并生成一个法方程，求解出由整个滑动窗口中48h数据求出的卫星初始轨道和力模型参数，利用轨道积分的方法得到48h的轨道以及以后6h的预报轨道，以此类推。这样，只需要快速解算当前天的6h短弧段法方程，以当前6h短弧段法方程之前的7个6h短弧法方程作为先验法方程信息，从而实现近实时精密轨道的快速更新，下表为短弧段建立过程中采用的测量模型和力学模型[6-8]。

2.2 算例分析

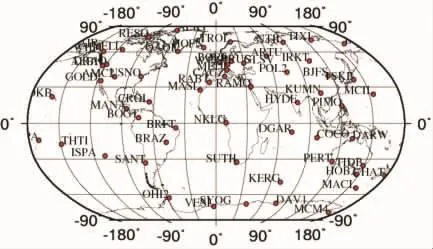
图2 全球分布的60个IGS站

本文基于2018年年积日89天～91天60个全球均匀分布的IGS站的观测数据，IGS站的分布如图2所示，利用BERNESE6.0软件解算GNSS导航星座的近实时精密轨道，然后与CODE提供的精密轨道做差，求算其RMS以评价解算近实时精密轨道的精度。以2018年年积日91天0点至6点的观测数据形成的6h短弧段法方程作为当前观测数据形成的6h短弧法方程，然后与其之前紧邻的7个6h短弧段法方程进行叠加。

图3为利用2018年年积日91天0点至6点的观测数据解算的各颗卫星6h弧段轨道精度（RMS），图4为当前6h观测弧段与此观测弧段之前紧邻的7个6h短弧段叠加之后的当前6h短弧段的轨道精度（RMS）。从中我们可以看出，利用当前6h的观测数据进行GNSS导航星座精密轨道解算，由于地面跟踪站对GNSS卫星的观测弧段长度有限，没有足够的观测数据进行约束导致各颗卫星的轨道精度比较低，不过大部分卫星的轨道精度都在1m范围以内，GNSS导航星座中所有卫星的总误差径向、切向、法向分别为 0.873m、0.374m和0.395m，平均为0.547m。这是由于GNSS导航星座中卫星的观测数据量比较少的缘故。所有的短弧法方程叠加之后，GNSS导航星座中各颗卫星的轨道精度都有了明显的提高，GNSS导航星座中所有卫星的总误差径向、切向、法向分别为0.067m、0.069m 和 0.064m，平均为0.067m，且GNSS导航星座中每颗卫星的轨道精度都是稳定可靠的[8-11]。

图5为短弧法方程叠加之后预报6h的轨道精度（RMS），即GNSS导航星座近实时轨道的精度。从中可以看出，短弧法方程叠加之后近实时轨道精度在径向、切向、法向分别为0.078m、0.120m和0.064m，平均为0.088m，可以看出本文解算的GNSS近实时轨道精度无论径向、切向还是法向轨道精度都相对比较高，且GNSS导航星座中每颗卫星的轨道精度都是稳定可靠的。

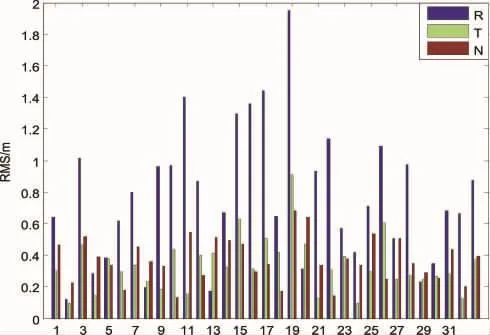
图3 叠加之前当前6h弧段的轨道精度（RMS）

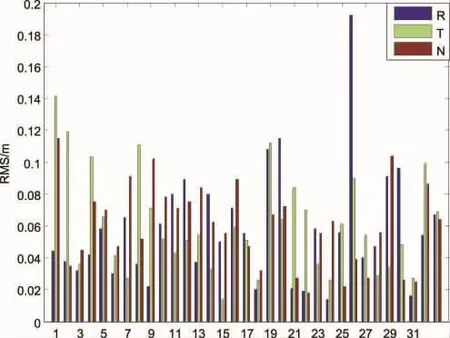
图4 叠加之后当前6h弧段的轨道精度（RMS）

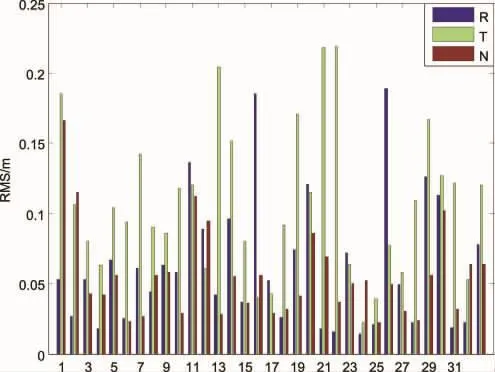
图5 预报6h（近实时）的轨道精度（RMS）

3 结论

本文详细地论述了GNSS导航星座近实时精密轨道的解算方法。基于全球均匀分布的60个IGS站的观测数据进行GNSS导航星座近实时精密轨道解算，其解算精度在径向、切向、法向分别为0.078m、0.120m和0.064m，平均为0.088m。本文解算的GNSS近实时轨道精度无论径向、切向还是法向轨道精度都比较高，并且本文解算的GNSS导航星座中每颗卫星的轨道精度都是稳定的，说明本文采用的滑动数据窗口内短弧法方程叠加的方法是可行的。