考虑渐进损伤的纤维缠绕复合材料圆筒铺层顺序优化设计①
颜 标,郭凯特,校金友
(1.中国电子科技集团公司第三十八研究所,合肥 230088;2.西北工业大学 航天学院,西安 710072)
0 引言
纤维缠绕复合材料圆筒由于其高比强度、比模量、轻质化和良好的抗腐蚀等优越性能,目前正被广泛用于航空航天和石油化工等领域[1-7]。复合材料的设计和制造过程参数严重影响着最终结构件的力学性能,因此如何确定纤维缠绕复合材料圆筒的设计及制造参数(铺层顺序、缠绕角、纤维体积分数和张力梯度等参数),最大化其刚度和强度,同时尽可能的减轻构件质量,一直是工程设计中不断追求的目标。实验和理论研究表明,铺层顺序和缠绕角对于缠绕壳体的质量和力学性能有着重要的影响[8-11]。对于复合材料纤维缠绕圆筒而言合理的铺层顺序,不仅能够提高圆筒的强度和刚度,还能减小复合材料圆筒的质量。对于内压载荷下的复合材料圆筒,网格理论表明最佳缠绕角度是±55°,然而网格理论未考虑基体的作用,同时该结论又是将铺层形式先定位±θ下所获得的结果,并不一定是最佳结果,因为实际每一层铺层角均可以变化即铺层形式并不确定。因此,在铺层形式未确定的情况下,研究特定载荷工况下复合材料圆筒的最佳铺层形式对提高圆筒承载性能具有重要意义。
近十年来,采用智能优化算法寻找复合材料层合板或者复合材料圆筒最佳铺层顺序,众多学者进行了研究。Park[10]运用GA、第一剪切理论与Tsai-Hill失效准则优化了对称铺层层合板在不同外载和不同边界条件下的铺层序列 ,使其承载能力最强。Pelletier[11]运用多目标遗传算法优化了承内压圆筒的铺层,使得爆破压强与环向刚度均满足设计要求。Rich与Haftka[12]以及Nagendra[13]等优化了复合材料平板的铺层,使其屈曲强度最大。Soremekun[14]运用GA优化了弯-扭耦合复合材料梁的铺层,使其强度最大。Martins[15]通过实验与模拟均发现当复合材料结构失效(最终失效)强度要大于功能失效(初始损伤)强度,而且优化铺层时所采用的强度计算方法对优化结果有很大的影响。Mertiny[16]通过实验方法研究了双轴载荷作用下铺层顺序对于复合材料圆筒强度的影响规律,结果表明铺层顺序对于结构最终失效模式及极限载荷有显著影响。Tabakov[17]基于3D弹性力学理论,结合Tsai-Wu失效准则,以最大爆破压强为目标,优化了复合材料圆筒的铺层顺序,结果表明优化的铺层并非常规铺层,没有明显规律。目前,虽然以强度为目标函数的复合材料铺层优化研究很多,但大部分是基于首层失效,未考虑渐进损伤,而复合材料损伤是渐进式的,出现初始损伤之后,载荷会重新分配,结构还能继续承载。因此,基于初始损伤与GA优化出的铺层不一定意味着结构具有最大的结构失效强度,有必要在铺层优化设计中考虑结构渐进损伤行为,研究铺层参数对圆筒结构极限强度的影响规律。
采用有限元进行渐进损伤包含两个步骤:损伤准则和损伤演化。损伤准则用来判断损伤的起始,损伤演化来控制损伤的扩展。关于失效准则,首先提出来的是唯象失效理论,该类失效理论依赖于大量精确的实验数据,运用多项式将不同失效模式耦合起来,例如Tsai-Wu失效模式、Tsai-Hill失效模式、Hollfman准则等[18]。Hashin和Rotem[19]首先提出了基于损伤机理的新一代损伤准则,分开考虑不同损伤模式,该准则将复合材料损伤分为基体损伤与纤维损伤,其中基体损伤考虑了剪切与拉压的相互作用,采用了二次耦合关系。Puck[20]与Schurmann[21]将Mohr和Coulomb理论[11]引入Hashin准则,提出了失效平面与失效角的概念,并重新推导出了纤维与基体的损伤准则并提出了Puck准则,但是该准则十分复杂,包含许多需要实验拟合的参数。后来,Davila[22]基于Puck准则,提出了LaCR准则,不包含任何拟合参数,所有参数都具有明确的物理意义。因此,本文复合材料圆筒损伤起始采用该准则。
本文采用遗传算法和复合材料结构渐进损伤理论,针对无约束条件以及缠绕工艺与环向刚度约束下三种工况,寻求内压载荷下使得结构性能最佳的铺层顺序。遗传算法基于Matlab平台实现,渐进损伤采用Abaqus软件实现,采用Python语言读写文件,建立两个软件平台之间信息传递桥梁,搭建起一种内压载荷作用下考虑渐进损伤的复合材料圆筒铺层优化方法,并对结果进行了分析讨论。
1 复合材料圆筒有限元模型
本文采用的有限元模型为8层纤维缠绕圆筒,由于该圆筒为缠绕制成,因此铺层模式为均衡铺层,即[±θ1±θ2…±θn]。为减小计算量,取1/8结构分析。其边界条件如图1所示,环向与圆筒右端为对称边界,左端为端部封闭边界条件,即固定1,2方向的位移,沿筒身方向自由,且其端部载荷为
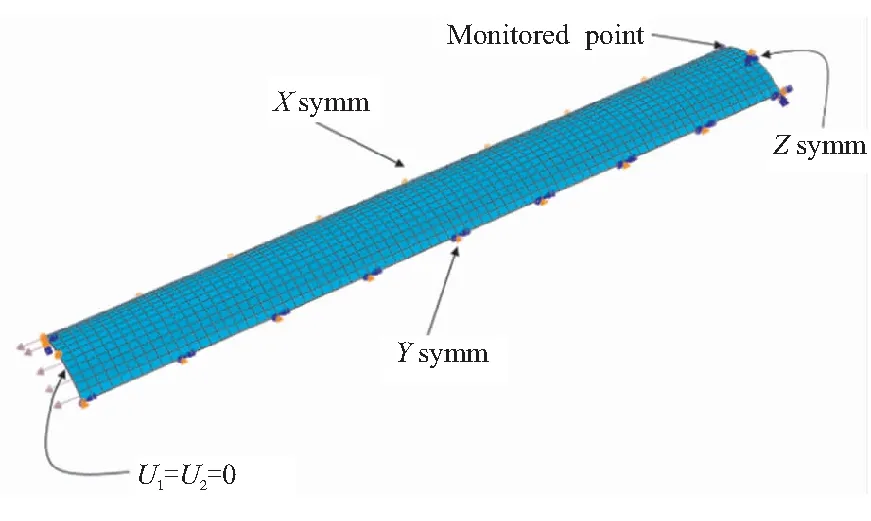
图1 圆筒有限元模型Fig.1 Finite element model of cylinder
(1)
式中p为圆筒承受内压;r为圆筒内半径;r1为圆筒外径;σA为圆筒端部表面压强。
本文采取的圆筒模型内半径r=50.8 mm,厚度t=2.75 mm,长度L=1100 mm,材料采用Glass/Epoxy复材,参数取自文献[23],如表1所示。模型划分单元数目为环向15个,轴向80个。采用C3D8R单元,层间性能用基体性能近似替代。沙漏控制为Enhanced。圆筒的破坏通过监控点(图1右上角)径向位移-内压曲线判断。

表1 复合材料单向板材料性能Table 1 Mechanical properties of composite
2 复合材料圆筒损伤起始及损伤演化
在对复合材料圆筒进行渐进损伤分析时,首先应给出相应的复合材料起始损伤判据。由于LaCR准则不仅预测精度较高,不包含任何拟合参数,且所有参数都具有明确的物理意义。本文运用LaCR准则来预测复合材料的面内损伤,LaCR准则是基于损伤机理推导出的,损伤模式分为四种:纤维拉伸损伤、纤维压缩损伤、基体拉伸损伤与基体压缩损伤。下面针对这四种损伤模式做以叙述。
2.1 损伤起始准则
(1)基体拉伸失效
图2给出了各种载荷作用下复合材料断裂平面示意图。其中,横向拉伸和面内剪切产生的断裂平面均与纤维方向平行,LaCR准则的基体拉伸失效考虑了拉伸与剪切的耦合,其表达式如下:
Fmt=(1-g)σ22/YT+g(σ22/YT)2+(τ22/SL)2
=1
(2)
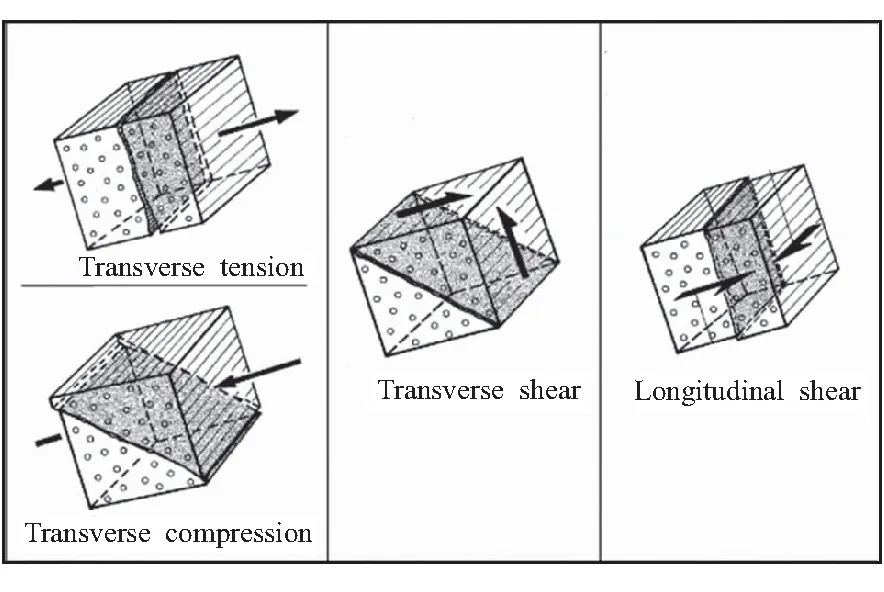
图2 不同载荷下断裂平面Fig.2 Fracture plane under different loads
式中g=GⅠ/GⅡ,GⅠ为一型裂纹断裂韧性,GⅡ为二型裂纹断裂韧性;YT为横向拉伸强度;SL为纵向剪切强度。
(2)基体压缩失效
基体压缩损伤较为复杂,基体损伤的失效平面的法向方向n与横向压缩载荷方向成一定的夹角α,如图3所示。
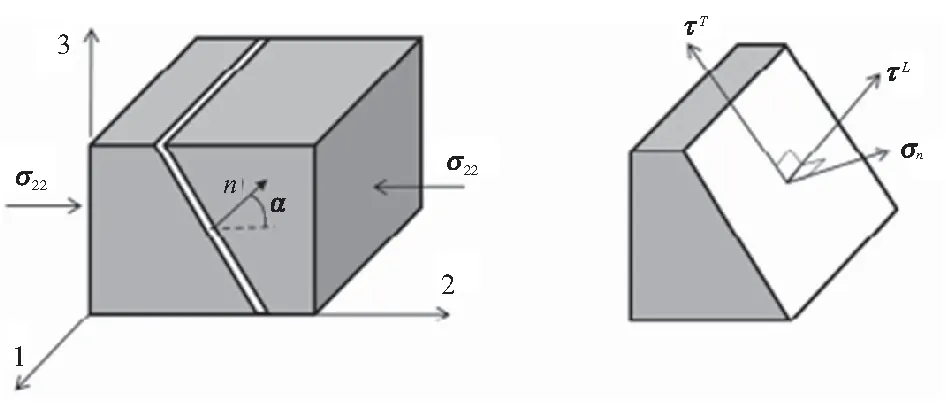
图3 压缩损伤失效平面Fig.3 Failure plane of compression damage
将直角坐标系应力绕1轴旋转α度得到:
(3)
σn对失效平面的压缩会产生摩擦力,会削弱剪切应力对损伤的影响。因此,用等效切应力来描述失效平面的切应力:
(4)
其中,
(5)
式中YC为横向压缩强度;α0为失效平面法向方向与2方向的夹角,α0根据Puck实验数据, 一般取53°。
LaCR准则运用二次相互作用来描述基体的压缩损伤:
(6)
其中,〈·〉为Cauley算子,定义为
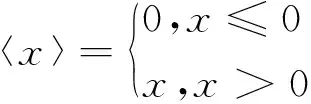
(7)
(3) 纤维拉伸损伤
对于纤维拉伸损伤,最大应力准则便能给出满意的结果:
(8)
(4)纤维压缩损伤
纤维压缩损伤较为复杂,其失效准则直到现在仍然在不断的发展中。许多研究认为,纤维的损伤是由基体失效引起的纤维屈曲导致的[24]。
LaCR准则采取了相同的观点推导纤维的压缩损伤准则,假设纤维的局部弯曲角度为φ,如图4所示。可以算得局部坐标系下的应力状态为:由于基体的拉伸与压缩损伤准则表达式不同,因此将分基体受拉与受压来给出纤维的压缩损伤准则。当基体受拉时,将式(9)代入式(2),可得式(10)。
(9)
(10)
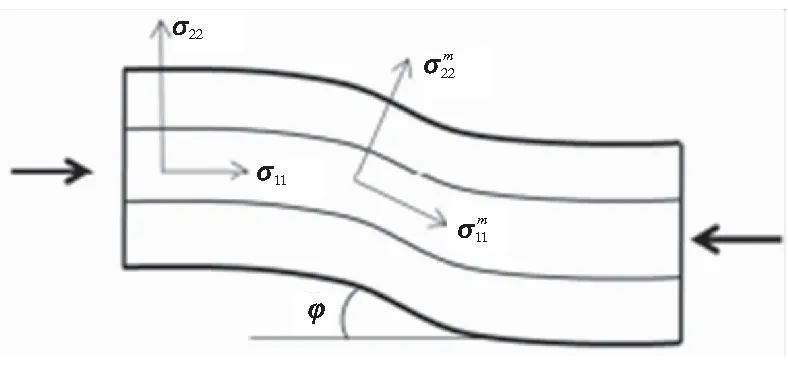
图4 纤维局部屈曲失效模式Fig.4 Failure mode of local fiber buckling
当基体受拉时,其失效准则表达式如下:
(11)
其中,局部屈曲角φ表达式如下:
(12)
(13)
2.2 损伤演化
当材料发生损伤时对材料刚度矩阵进行折减。纤维与基体损伤分别用变量df与dm描述,那么当损伤发生后的刚度矩阵可表示为
(14)
其中,K=1-(1-df)(1-dm)ν12ν21,E11、E22、G12、ν12、ν21为材料弹性参数。当完全损伤发生后,若直接将刚度矩阵相应分量折减为0,会引起刚度矩阵奇异。因此,当完全损伤后df(m)一般不取1,可取一个十分接近1的值,本文取1-10-6。
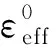
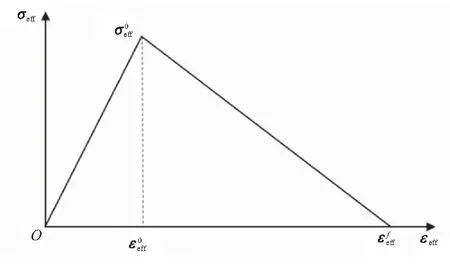
图5 双线性损伤演化准则Fig.5 Bilinear damage evolution criterion
由于损伤的不可逆性,损伤变量只能单调增加,且其值不能大于1:
(15)
在有限元中运用应变软化模型会导致严重的网格依赖性,损伤过程的能量耗散与网格大小相关,为缓解网格的依赖性,本文采用Bazant提出的裂纹带模型(Crack band model),认为裂纹产生所耗损的能量应该等于裂纹表面形成所需的能量即断裂韧性:
(16)
式中Gc为断裂韧性;Lc为单元特征长度。
该方法不仅有效缓解了有限元模拟过程的网格依赖性,同时将损伤过程的能量耗散与实际物理量断裂韧性联系起来了,更加符合实际。
材料本构模型存在应变软化或性能衰退会导致收敛困难,采用粘性正则化可以改善收敛性,该方法在计算损伤演化时不使用当前损伤变量,而是使用正则化后的损伤变量:
(17)
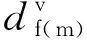
3 考虑渐进损伤的圆筒铺层优化方法
遗传算法是模拟达尔文生物进化论的自然选择和孟德尔遗传学机理的生物进化过程的计算模型,是一种通用模拟自然进化过程搜索最优解的方法。求解的过程主要由问题的数学建模、基因编码、适应度函数求解与运用遗传算子生成下一代四部分组成。以上过程反复迭代求解直到求出满足要求的解或迭代步数达到指定值,遗传算法的主要过程可分为编码、解码、杂交、突变和个体适应度评价几个步骤。
本文的遗传算法优化模型在Matlab中实现,爆破内压运用渐进损伤模型预测,在商业有限元软件Abaqus中实现。因此,铺层优化算法主要分为优化算法与有限元求解两部分组成,如图6所示。其中,黄色实线框内为GA算法求解过程,绿色虚线框内为有限元求解过程,GA算法模块与有限元求解模块的数据交流通过输入文件Sequence.in与输出文件Pressure.out进行桥接。
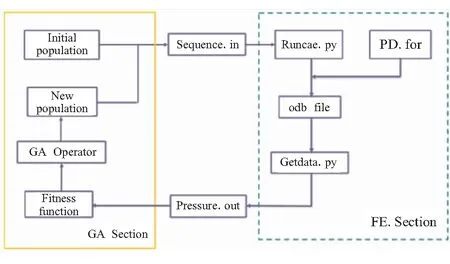
图6 铺层优化流程图Fig.6 Flow chart of optimization process
上述铺层优化算法计算过程可总结为:初始种群产生后,将其铺层序列写入文件Sequence.in中,然后Python程序Runcae.py从中读入铺层序列建立CAE模型,并调用渐进损伤子程序PD.for进行承内压圆筒有限元分析,完成后生成结果文件,运用Getdata.py脚本读出爆破内压并写出到文件Pressure.out中,最后将爆破内压作为个体适应度返回到GA部分并生成下一代种群。在本次遗传算法求解中,杂交概率取100%,突变概率取2%,种群数目取20,最大迭代次数取50。
4 基于遗传算法的复合材料圆筒铺层顺序优化
4.1 复合材料圆筒有限元模型验证
为进一步验证上述损伤模型预测圆筒爆破压强的准确性,运用该模型计算[±45]4与[±60]4铺层的圆筒爆破内压并与实验对比,图 7为圆筒内压与监测点径向变形关系图,可看到[±45]4铺层在压强达到8.34 MPa时,径向位移急剧增加,即圆筒破坏。
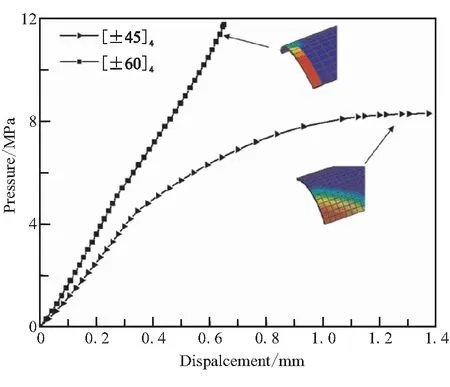
图7 压强-监测点位移关系曲线Fig.7 Curves between pressure and monitoring node displacement
对于[±60]4铺层,当圆筒爆破内压达11.7 MPa时失效,但径向位移并未急剧增加,这主要是由于该铺层下失效模式为圆筒中部轴向失效,此时轴向位移急剧增大后圆筒失效。损伤模型预测强度值与实验值对比如表2所示,实验值取自文献[26]。两种铺层下误差分别为1.65%与11.3%,验证了上述损伤模型的准确性,接下来将运用基于上述损伤模型与GA的铺层优化算法对承内压复合材料圆筒进行铺层设计。
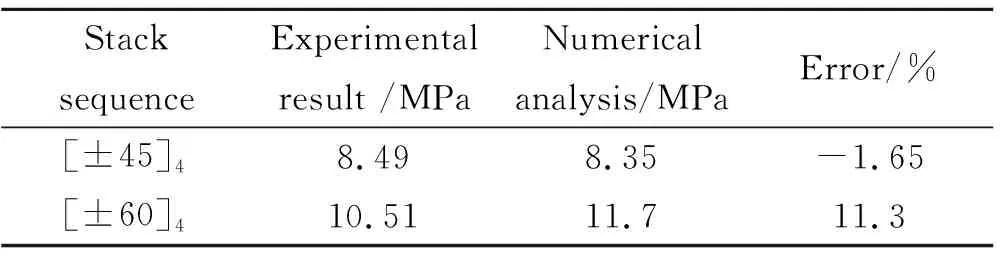
表2 实验与模拟爆破压强对比Table 2 Comparison of burst pressure for experiment and simulation
4.2 无约束的铺层设计
图8为铺层角度无约束下的优化,大概30代后达到最大爆破压强17.56 MPa,平均爆破压强不断增加直到22代后在稳定值附近波动,平均值没有趋近于最大值是由于通过遗传算子杂交、变异等产生的下一代中总可能包含非最优解。正是由于此,遗传算法可跳出局部最优从全局寻求最优解,而不是收敛到局部最优。该种工况(#1)下优化出的最佳铺层如表3所示。
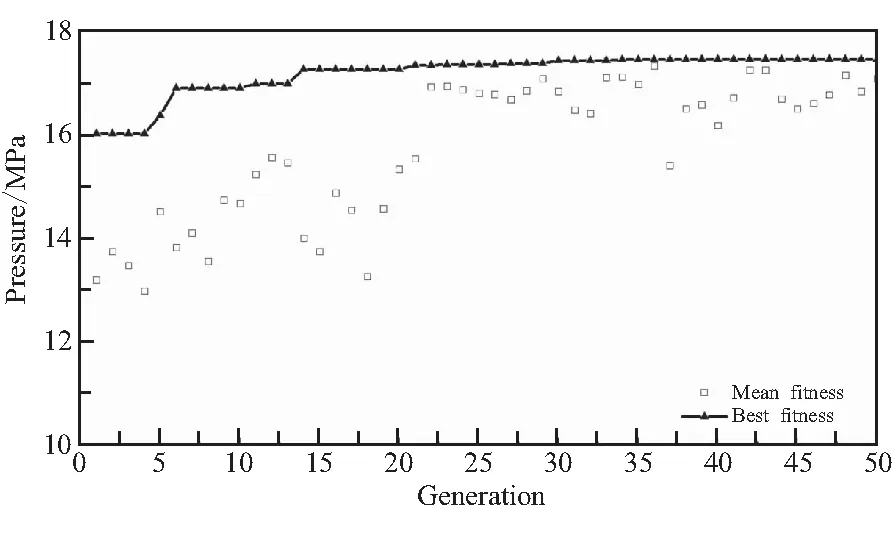
图8 无约束情况下铺层设计Fig.8 Stacking sequence design under unconstrained condition
可看到,在考虑渐进损伤优化出的铺层没有规律,而实际生产中,一般采用均衡反对称铺层[±55]4。实际上圆筒承受内压时,当某些层损伤后,圆筒原有的铺层规律也将消失,Pelletier[11]与Irisarri[8]运用GA优化出的层合板铺层序列也没有规律。而工业上优化出的铺层有规律是由于其优化前假设的铺层序列就具有规律,如假设铺层序列为[±θ]n。
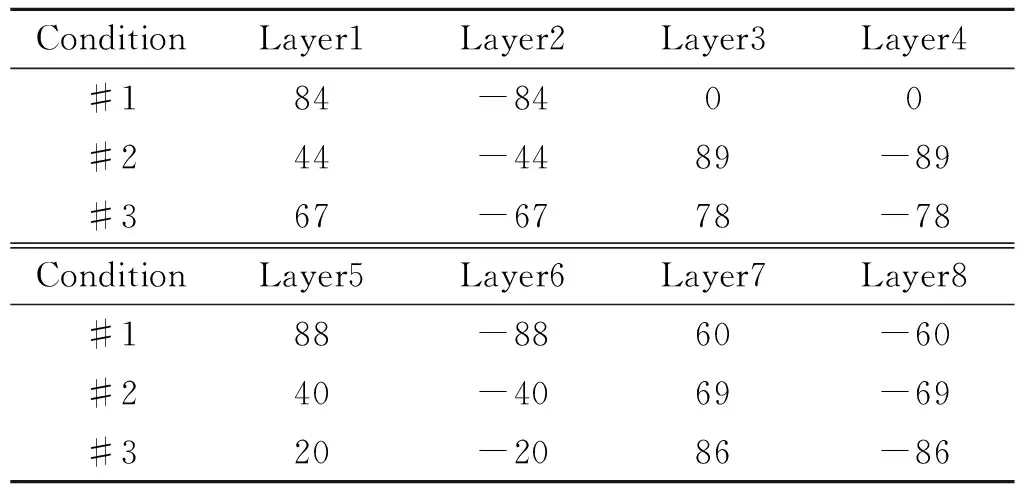
表3 不同约束条件下优化的最佳铺层序列Table 3 Optimized stacking sequence under different constrains
图9对比了[±55]4铺层与优化出的铺层的压强-检测点位移关系曲线,可以看到优化出的铺层爆破压强为17.58 MPa,大于传统采用的[±55]4铺层。可以发现,两种铺层下基体损伤的产生均远早于最终失效,当纤维失效后结构不再能承受更大压强,纤维失效意味着最终失效说明铺层较为合理,因为充分发挥了纤维的高强度特性。同时,可发现优化的铺层具有更大的刚度,这主要是由于在承力方向上布置了更多的纤维,这也导致了更大的爆破压强。此外,优化出的铺层的失效应变更小,这主要是由于优化出的铺层在承力方向上具有更多纤维,因此导致了比[±55]4铺层提前出现最终失效(失效位移更小)。
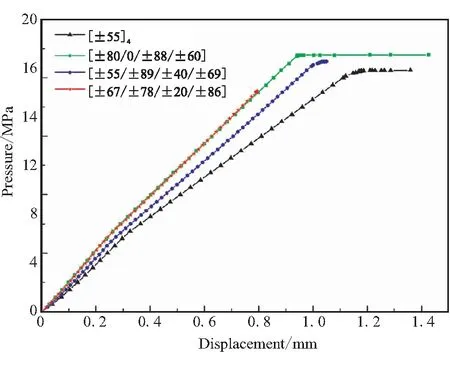
图9 不同条件下优化铺层的压强-检测点位移曲线Fig.9 Curves between pressure and monitoring node for optimized stacking sequence under different constrains
4.3 制造工艺约束下的铺层设计
由于封头与摩擦系数的限制,缠绕工艺中纤维的缠绕角不能过小,否则无法在封头处从+θ角过渡到-θ。本文根据圆筒尺寸与摩擦系数限制缠绕角不能小于20°。由表3看到无约束条件下优化出的铺层为[±84/±0/±88/±60],其中的0°铺层无法缠绕。因此考虑工艺限制,上述铺层在实际生产中无法实现,现在工艺限制下对铺层进行优化。
图10为考虑工艺约束下的铺层优化结果,可以看到在第12代后到达最大压强17.11 MPa。平均值与无约束条件下一样,在不断波动中趋于稳定值,在27代后便在最大值附近波动。此种情况下优化的铺层角为[±44/±89/±40/±69],所有角度均在要求内,而且优化出的角度也没有明显规律。将该铺层角度下的位移压强绘制在图9中,如蓝色曲线所示,其压强略小于无约束下的铺层。同时,可发现不同铺层形式下基体损伤的时间差别不大,纤维的损伤的时间差别较大,爆破压强越大纤维损伤的时间越早。
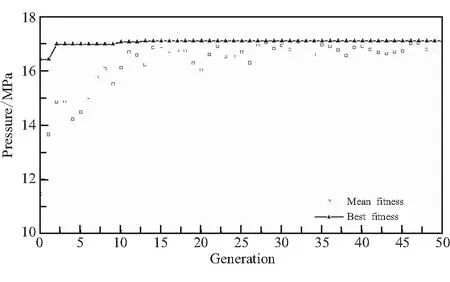
图10 制造工艺约束情况下铺层设计Fig.10 Stacking sequence design under manufacturing constrains
4.4 刚度约束下的铺层设计
本节针对高刚度、高强度要求进行约束,其中强度同样由渐进损伤模型给出。对于刚度,其可由损伤发生前的压强-监测点位移曲线获得,但是每次均调用Abaqus将带来巨大的计算量,使得计算效率较低,因此在本次优化中刚度由层合板理论计算得到。当给出铺层模式后,首先在Matlab中计算该铺层模式下的环向刚度E_y,若环向刚度小于指定值E_0,则直接跳过调用Abaqus,并将适应度函数直接赋值为0,从而该铺层序列会在后续迭代中迅速被淘汰。只有刚度满足要求的铺层才会调用Abaqus计算强度,从而减小计算量,本次模拟中E_0取20 GPa。
图11为刚度约束下优化结果图,20代后压强到达稳定值15.09 MPa,平均值与上文两种情况类似,在震荡中慢慢趋于稳定。优化出的铺层为[±67/±78/±20/±86],可看到角度均大于等于20,符合工艺要求。将该铺层下的爆破压强-监测点位移曲线绘制在图9中如红色曲线所示,压强明显小于其余铺层模式。同时,可看到与绿色曲线斜率(刚度)基本一样,但绿色曲线(无约束下铺层应力应变曲线)对应的铺层不符合工艺约束,其存在0°层。而且该铺层模式下圆筒破坏时参考点径向位移没有发生突变,这主要是由于该铺层下失效模式为圆筒中部轴向失效,此时轴向位移急剧增大后圆筒失效。对比图中四条爆破曲线,可看到[±55]4不仅强度较小,同时刚度也较小,并不是最合适的铺层,相比于[±55]4铺层,本文给出的铺层具有明显优势。
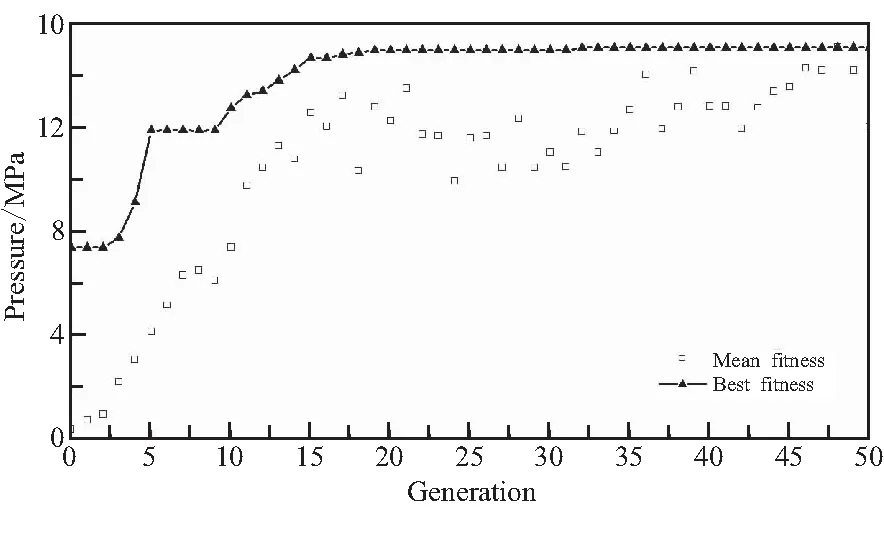
图11 刚度约束下的铺层设计Fig.11 Stacking sequence design under constrained modulus
5 结论
(1)建立了内压载荷作用下复合材料圆筒铺层顺序优化方法,该方法考虑了复合材料渐进损伤过程。优化算法基于Matlab平台建立,渐进损伤分析基于Abaqus软件平台分析。采用Python语言编写脚本进行两个软件平台的数据交换,搭建了基于Matlab和Abaqus软件平台的复合材料圆筒铺层顺序的优化设计平台。
(2)基于本文所建立的复合材料渐进损伤分析方法,对[±45]4与[±60]4铺层的圆筒爆破内压并与实验对比。结果表明,误差在13%以内,从而验证了本文渐进损伤模型的正确性,为后续铺层顺序的优化奠定了基础。
(3)基于搭建的复合材料圆筒铺层顺序的优化平台,对三种工况条件下的铺层优化做了分析计算。结果表明,无约束条件和考虑工艺约束条件下所得到的铺层均无明显规律,无约束条件下爆破压强和考虑工艺约束下的爆破压强均高于传统铺层[±55]4所对应的爆破压强,分别高出6.5%和3.7%,说明该方法可在一定程度上提高复合材料圆筒的爆破压强。

