基于Simulink的地电波检测机械臂>运动控制器及动力学研究

姚 明，周 敏，王 婧

(1.国网上海市电力公司市北供电公司，上海 200072；2.上海服泽能源科技有限公司,上海 200025)

地电波检测是变电设备日常巡检的一种重要且有效的手段。本文将地电波检测机械臂装置与移动电力巡检机器人结合起来，能够实现地电波自动巡检功能。地电波机械臂涉及结构设计、运动学、动力学、控制器设计等很多方面，本文主要研究地电波机械臂的动力学问题，使用牛顿-欧拉法建立地电波机械臂的动力学模型[1-5]。在MATLAB中对地电波检测机械臂的动力学模型进行仿真。

1 地电波检测机械臂介绍

1.1 机械臂结构

机械臂包含五个转动关节和一个两手指的末端夹持器。它可以到达655 mm的高度，质量为6.3 kg，设计能够夹持质量0.5 kg的物体。在机械臂保持竖直姿态的情况下，关节1和关节5可以绕着相互平行的转动轴进行转动。

1.2 机械臂操作系统

机器人操作系统(Robot Operating System，简称ROS)是机器人控制领域流行的应用开发环境，包括提供硬件抽象、设备驱动、可视化器、消息传递等的库和工具，可以创建ROS节点与节点管理器连接。每个连接到节点管理器的节点都可以通过订阅相应的主题来收听其他节点提供的所有消息[6-10]。除了消息之外，参数和服务可以以相同方式用于连接到节点管理器的所有节点。用户通过编写节点发布消息或话题、服务来与其他节点通信。 KUKA-youBot有一个现成的ROS组件，它为ROS和直接访问硬件的youBot驱动程序之间的通信建立了一个接口。这使得可以通过youBot组件发布消息形成反馈控制来控制关节位置或速度。

2 机械臂动力学建模

2.1 动力学建模方法概述

地电波检测机械臂的动力学建模问题，即研究关节角度、关节速度、关节加速度等关节运动状态与各关节驱动力矩之间的关系。建立地电波检测机械臂的精确动力学模型并深入研究其动力学特性，为接下来设计机械臂动力学控制器实现精确实时运动控制打下基础。

对于如何建立动力学模型的方法，主要有牛顿-欧拉法、拉格朗日法等[1-5]。牛顿-欧拉法推导过程简单便于编程且计算比较快，对机械臂的每个构件分别运用牛顿方程和欧拉方程，适用于工业机械臂的动力学计算。但是其考虑不做功的内力、内力矩，并且方程为非封闭形式，消耗不必要的计算机时间。拉格朗日法基于总能量的标量函数推导其动力学方程。随着机械臂自由度数目的逐渐增加，计算次数显著增多。最近几年兴起的智能化动力学建模出现较大发展，比如模糊动力学模型、智能自适应模型等。智能化建模方法不依赖具体机械臂的动力学特性，方便对机械臂实施更高层次的控制。针对地电波检测机械臂的结构特点，本文采用牛顿-欧拉法为地电波检测机械臂建立逆动力学模型。

2.2 牛顿欧拉动力学建模

2.2.1 惯性张量

对于轴向转动的机械臂，采用惯性张量描述机械臂连杆的质量分布，可用3×3矩阵表示如下：

(1)

矩阵中的各元素：

(2)

(3)

(4)

(5)

(6)

(7)

其中，机械臂连杆由单元体dv组成，其关节连杆的密度为ρ。Ixx，Iyy，Izz称为惯量矩，Ixy，Iyz，Iyz称为惯量积，这六个独立的变量取决于所在连杆坐标系的位姿。随着连杆质心坐标系的旋转，当连杆惯性张量中的惯量积为零时，此时连杆坐标系的坐标轴成为连杆主轴，惯量矩称为主惯性矩。根据惯性张量的特点，可以根据地电波检测机械臂各个连杆的质心坐标系位置和惯性张量确定该机械臂的质量分布。

2.2.2 牛顿—欧拉动力学方程

牛顿—欧拉动力学方程描述了关节力矩和关节运动状态之间的数学关系。根据其定义方法，对于可动关节均为转动关节的机械臂来说，该算法的运算过程如下：

外推：

(8)

(9)

(10)

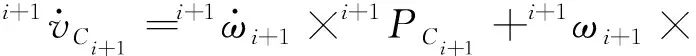
(11)

(12)

(13)

内推：

(14)

(15)

(16)

2.3 地电波检测机械臂动力学建模

将地电波检测机械臂的惯性张量，连杆质量，质心矢量，旋转矩阵，关节角度、速度、加速度等参数带入方程中便可计算出关节力矩。

连杆质心位置(mm)：

1Pc1=(15.16 -3.59 -31.05)

2Pc2=(113.97 -15 19.03)

3Pc3=(104.41 0.13 -20.22)

4Pc4=(-0.15 53.53 24.64)

5Pc5=(0 1.2 -16.48)

连杆主惯性矩(kg·m2)：

l1xx=0.002 952 5;l1yy=0.006 009 1;l1zz=0.002 882 1

l2xx=0.003 114 5;l2yy=0.000 584 3;l2zz=0.003 163 1

l3xx=0.001 727 67;l3yy=0.000 419 67;l3zz=0.001 846 8

l4xx=0.000 676 4;l4yy=0.001 057 3;l4zz=0.000 661 0

l5xx=0.000 193 4;l5yy=0.000 160 2;l5zz=0.000 068 9

连杆质量(kg):

m1=1.390,m2=1.318,m3=0.821,m4=0.769,m5=0.687

采用牛顿—欧拉方程，可以将得到的动力学结果可以写成如下状态空间的形式：

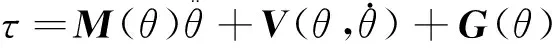
(17)

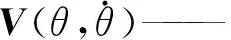
因式(17)中的矢量取决于位置和速度，也称为状态空间方程：

(18)

(19)

3 基于MATLAB的动力学仿真

在MATLAB中对地电波检测机械臂的动力学模型进行仿真。根据地电波检测机械臂的关节角度、关节角速度和关节角加速度等运动状态可以通过计算得到关节驱动力矩，仿真结果如图1所示。

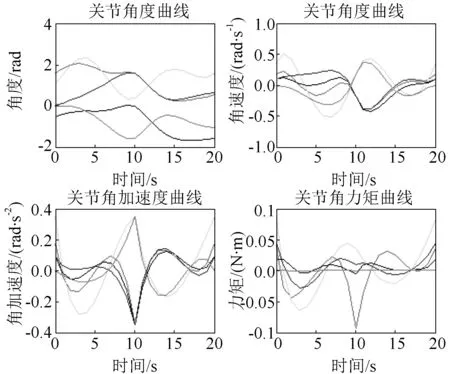
图1 动力学仿真结果

4 动力学控制器设计

基于地电波检测机械臂动力学模型设计控制器，并在Simulink与Gazebo环境下进行仿真，以达到了良好地控制效果，为接下来更先进的控制器设计打下基础。

4.1 控制器设计

地电波检测机械臂是一个非线性耦合动力系统，在运动控制过程中必然存在各种不确定因素增大了其控制难度，因此对其控制器设计与分析具有重要意义。控制难点具体如下。

(1)参数不确定：如机械臂的负载等参数的变化。

(2)外干扰：如电机驱动饱和、传感器测量误差、采样延时等。

(3)强非线性：传动摩擦力、振动误差、响应滞后等。

4.2 控制器设计

地电波检测机械臂的控制问题是一个多输入、多输出问题，可以把控制部分分解成基于模型的控制部分和伺服控制部分。

F=αF′+β

(20)

式(20)为基于模型的控制部分，对于5自由度的地电波检测机械臂来说，α代表5×5的解耦矩阵，起解耦作用。

(21)

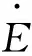
对于常见的机械臂动力学方程：

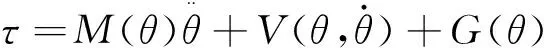
(22)

因此，可以利用控制器分解法设计如下控制器：

τ=ατ′+β

(23)

(24)

其中：

α=M(θ)

(25)

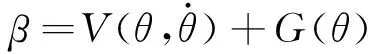
(26)

该控制系统模型如图2所示。

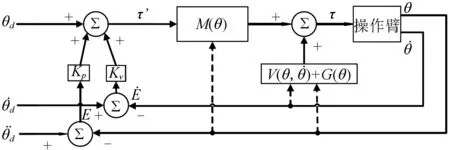
图2 基于模型的地电波检测机械臂控制

利用式(22)至式(26)，可以得到系统闭环误差方程：

(27)

由于Kv和Kp为对角矩阵，因此各关节是解耦的。

4.3 Simulink仿真

利用地电波检测机械臂动力学模型设计了该控制器，并在MATLAB的Simulink中搭建了仿真环境(见图3)，设计了地电波检测机械臂的动力学仿真模块，并测试了地电波检测机械臂各关节的阶跃响应。各关节的阶跃响应曲线见图4。

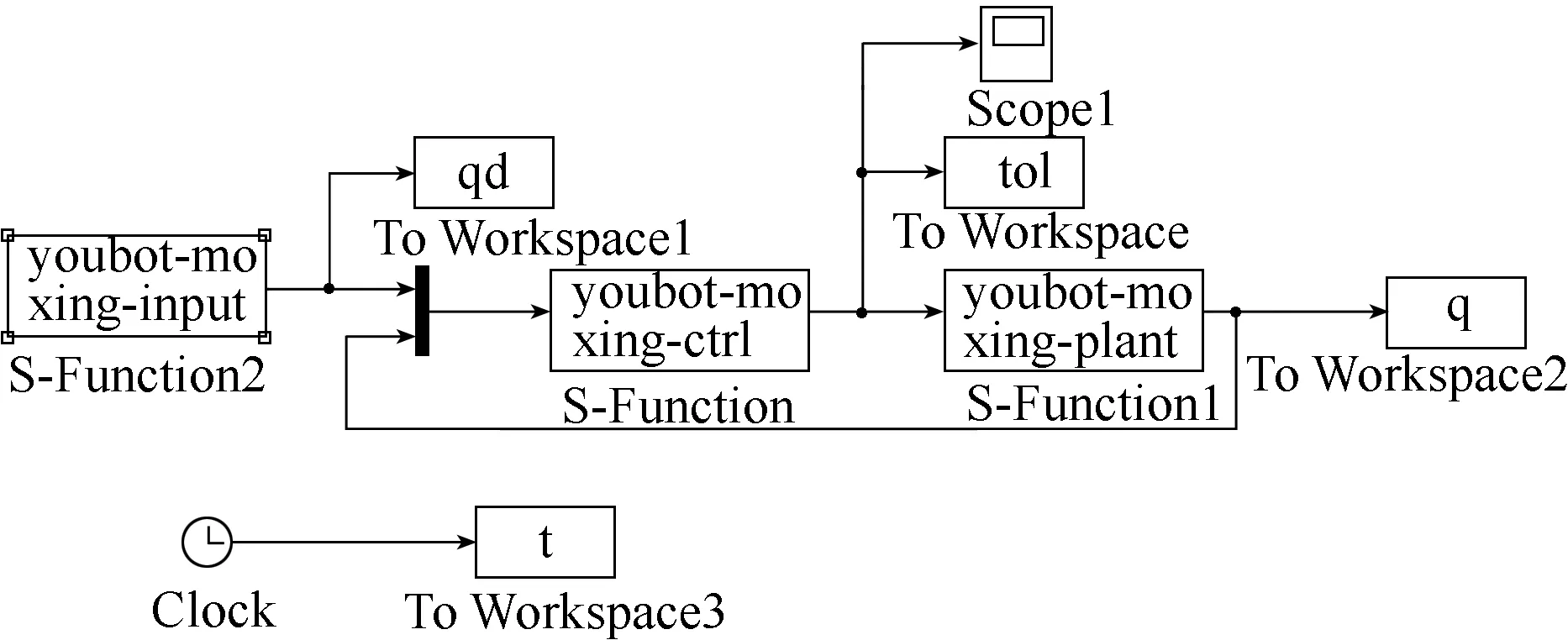
图3 Simulink仿真环境搭建

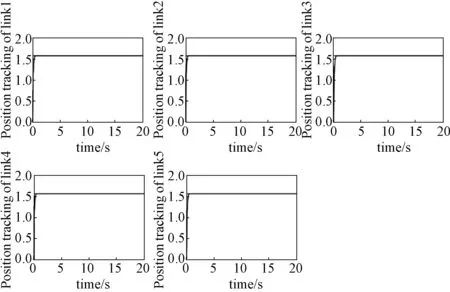
图4 各关节的阶跃响应曲线

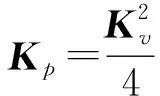
4.4 Gazebo仿真

Gazebo可以实现地电波检测机械臂的物理仿真，通过在ROS与MATLAB联合控制在Gazebo仿真环境下的地电波检测机械臂运动来实现控制效果。为了方便控制人机交互，采用MATLAB编写了上位机软件，其界面见图5。

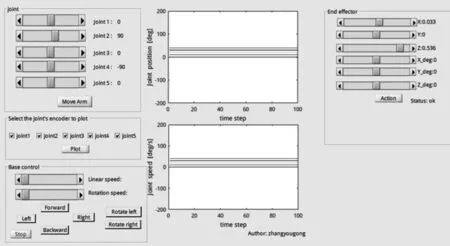
图5 地电波检测机械臂的上位机控制界面

5 结语

针对动力学建模问题，采用牛顿-欧拉法得到了其逆动力学方程。基于控制律分解方法设计了机械臂的运动控制器，并搭建了Simulink仿真模型，仿真结果显示了该系统良好的阶跃响应、轨迹跟踪性能。