基于团簇随机连接的CliqueNet航 班延误预测模型

屈景怡，曹 磊，陈 敏，董 樑，曹烨琇

（1. 天津市智能信号与图像处理重点实验室（中国民航大学），天津300300； 2. 中国民用航空华东地区空中交通管理局，上海200335）

0 引言

近年来，随着航空运输需求量增大，由于空域和天气等因素的限制，航班延误问题日益突出。另一方面，为贯彻全国交通工作会议精神，推进民航高质量发展，中国民用航空局空中交通管理局在2019 年提出了围绕质量变革、效率变革的发展需求［1］，围绕大数据、云计算、人工智能等数字信息化、智能化技术谋求发展空间已经成为行业普遍共识。目前，国内外学者在对航班延误预测、预警和维护航班正常运行等方面进行了大量针对性研究［2］。现有方法中多采用贝叶斯网络（Bayesian Network，BN）［3-4］、支 持 向 量 机（Support Vector Machine，SVM）［5］、随机森林［6-7］、人工神经网络（Artificial Neural Network，ANN）［8］等传统的机器学习算法。文献［3-4］中利用BN参数学习理论，从不确定和概率性知识信息的航班数据中通过推理得出规律结论，对关联机场的衔接航班延误影响进行分析，提出了基于BN 的航班延误传播模型；结合实际数据测试得到的结果表明该模型可以有效地分析航班延误从局部到全局的传播。文献［5］中使用SVM 给出了到港延误预测模型，采用空间重构理论计算到港延误的延误时间、嵌入维度和最大Lyapunov 指数等指标，发现到港延误时间序列存在的混沌特性；实验结果表明，该方法的预测结果明显优于粒子群优化和差分进化等预测算法。文献［6］中针对航空数据呈现高维化、海量化趋势，提出利用Spark 并行化方式进行随机森林的特征划分和树的生成：前者以快速的方式进行航班延误预测；后者对噪声和异常值具有更好的容忍性，克服了决策树过拟合问题。文献［7］中同时考虑时空延迟状态作为模型的解释变量，并且使用随机森林算法预测未来2～24 h 的起飞延误。网络中除了描述最有影响的机场和链路（始发—目的地对）的到达或离开延迟状态的局部延迟变量外，还描述了整个国家空域系统在预测时的全局延迟状态的延迟变量。该模型在2007和2008年运行数据上进行了训练和验证，并对系统中100 个最延迟的链路进行了评估，结果显示其预测性能远优于单一因素的预测模型。但是上述几个航班延误模型针对的数据样本相对较少，在面对高维度的样本时不能很好地拟合。

文献［8］中以肯尼迪国际机场（John F Kennedy International Airport，JFK）为例将ANN 应用到航班延误预测，在1/N 编码方式的基础之上介绍了新型的多级输入层神经网络，在某种意义上可以更容易得出输入变量和输出变量之间的关系。以肯尼迪机场为例，将该方法应用于航班延误预测，输入层各子层神经元代表系统不同层次的延误源，而各神经元的激活则代表系统整体延误源的可能性。ANN 虽然可以较好地拟合“延误源”等客观规律，但全连接神经网络没有克服模型加深无法收敛的问题，且预测准确率相对较低。

因此，针对上述问题，本文提出一种基于大数据的深度学习方法进行延误预测。目前，类脑智能研究［9］和神经网络在计算机视觉、自动驾驶、模式识别等领域均得到了广泛的应用，其性能远优于传统的统计学习算法。其中，卷积神经网络（Convolutional Neural Network，CNN）［10］取得了较大突破。残差网络（Residual Network，ResNet）［11］的提出，则很好地解决了训练深层网络产生的梯度消失的问题，真正意义上实现了“深度”学习。神经网络中仿生大脑的循环网络结构［12］是一种高效的信息传递网络结构。受其启发，团簇网络（Clique Network，CliqueNet）［13］以团簇连接方式最大限度地提高特征层之间的信息传递效率；并且对网络转换层中的通道［14］以及空间维度［15］进行特征重标定，可以有效提高网络的准确率。

本文在深入研究上述文献后，提出了一种更高效的随机连接CliqueNet 的仿生网络模型，用以提高对航班数据的处理能力；并针对不同的转换层进行讨论，充分结合其双重标定的优势，增强特征层传播的有用信息，抑制无用信息，提高预测准确率；最后在融合气象信息的航班数据上进行有效性的验证。

1 CliqueNet

本文所设计的CliqueNet 的基本结构如图1 所示，输入的数据经过模型特征提取之后给出预测结果。模型则由团簇和转换层（Transition）组成：团簇作信息的交互传递；转换层则嵌入在团簇之间，用于标定特征信息并且增加网络健壮性。

下面分别对模型中团簇和转换层进行介绍。

图1 CliqueNet的基本结构Fig.1 Basic structure of CliqueNet

1.1 随机连接团簇

考虑到航班延误预测模型需要更强的数据处理能力来拟合高维度的海量数据，对全连接团簇进行随机团簇连接的改进，因为某种意义上，随机连接的仿生网络结构能更好地拟合数据背后的客观规律。

全连接团簇的环状结构如图2（a）所示，将其展开，会呈现出两个阶段。第一阶段：仿照密集型连接卷积网络（Densely connected convolutional Network，DenseNet）［16］的连接方式，即每一层输入均来自前面所有层的输出，对整个网络进行初始化；第二阶段：每层的输入来自其他所有底层的输出。考虑到全连接方式［13］具有能进行最大化信息传递的优势以及网络参数随着层数增加而呈现倍数增长带来的缺陷，本文将团簇中的全连接方式改成随机连接，如图2（b）给出的连接实例，即第二阶段的顶层特征随机来自其他底层的特征输入。较之全连接方式，即省略虚线连接部分，这样的网络既可以实现特征层之间信息的有效传输，又可以降低网络的参数量；而且后期实验结果也表明，网络依然能保持较高的预测准确率。

表1给出了5层的团簇传播参数说明。在第一阶段，输入层X0对所有层进行初始化，且每个更新层与下一层相连，准备更新下一层。在第二阶段，各层的网络之间进行随机的传递（表1中展示了一个实例），如式（1）所示：

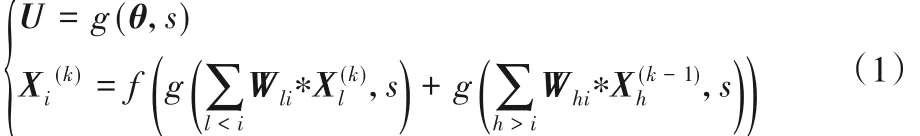
其中：分别表示相对于第i层)的前、后层的特征；k值表示第几阶段；Wli和Whi依次表示和前后层做卷积操作的参数，本文中卷积操作均用*表示。随机函数［17］g(θ，s)的参数θ表示输入特征值，参数s表示随机种子，U为网络提取后的特征值，例如：U=g(X0，3)表示初始化特征由顶层随机对3个底层做出特征传递。实验中为了继承CliqueNet中全连接中最大化信息传递的优势，将s从2 计数，即保证每层输入至少来自其他2 层的输入，最大取值为团簇中设置的层数，即s= range[2，layer_num]。f(·)表示非线性激活函数，用于参数传递的非线性映射。实验中由两层循环实现：第一层循环控制顶层的切换；第二层循环用于顶层与随机给出的底层之间的连接，并做信息传递。

1.2 转换层

除了上述结构之外，为了满足民航业高精度延误预测的要求和提高网络鲁棒性，本文还对图1 中的转换层进行优化以提高网络性能。基于压缩激励（Squeeze and Excitation，SE）模块［14］可以有效地对特征通道进行权重分配，而且其权重分配在反向传播时，网络会自适应调整参数，进而达到对融合航班和天气的数据集进行学习的目的，如图3 通道维度所示。此外，考虑到客观事实中航班延误可能受天空状况、能见度、湿度等局部维度数据影响较大，部分字段，例如航班尾号等对航班延误影响不是很大，故引入了能自适应调整局部维度数据的通道和空间注意力残差（Channel-wise and Spatial Attention Residual，CSAR）模块［18］，该模块在SE 模块的基础上对通道特征和空间特征进行双重标定，对不同的局部维度数据标定不同的特征权重，并利用非线性激活函数组成的门控机制学习通道和空间上的非线性交互，其结构设计（如图3所示）会使网络具有更多非线性，可以更好地拟合目标函数。

表1 五层团簇参数传播信息表Tab. 1 Propagation information table of 5-layer clique parameters

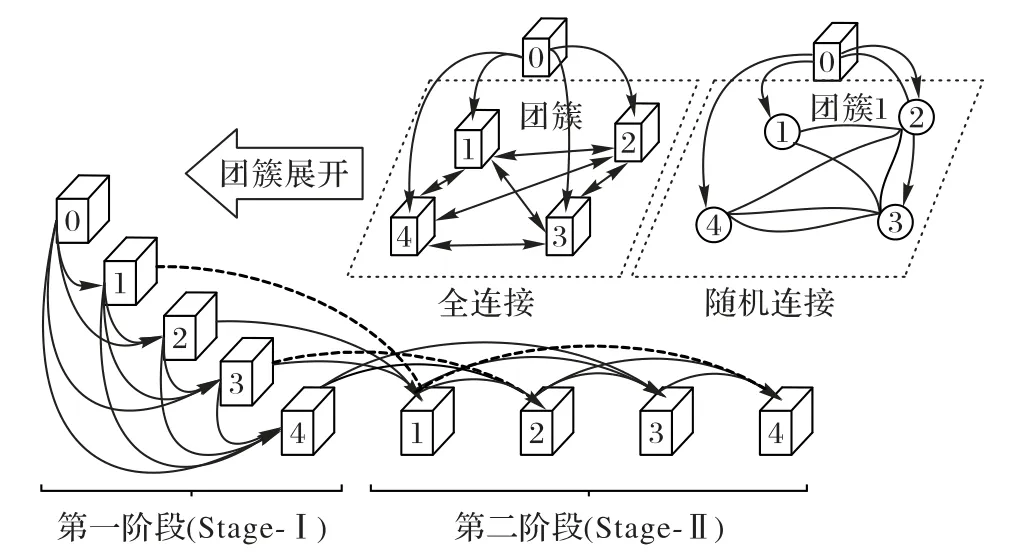
图2 团簇拓扑结构Fig.2 Topology of clique

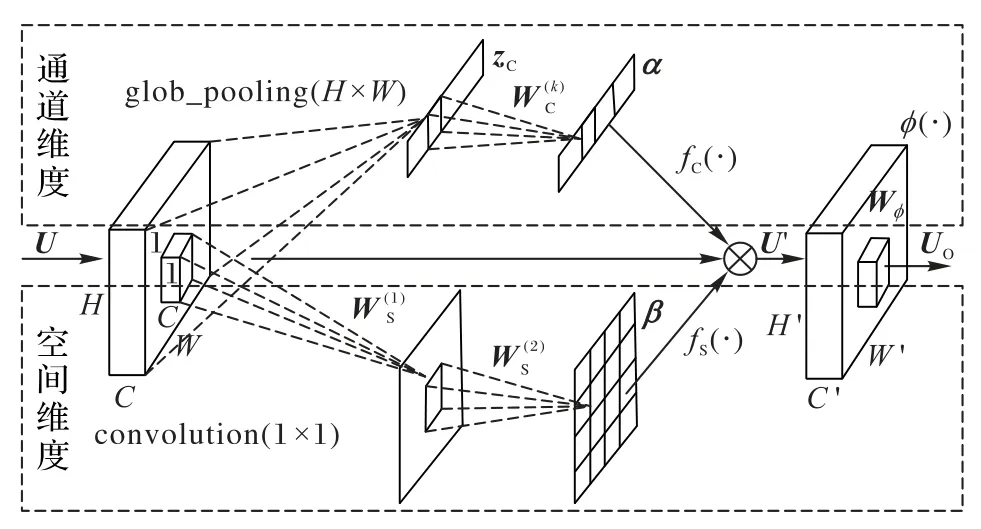
图3 转换层拓扑结构Fig. 3 Topology of transition layer

CSAR 模块中，U=[u1，u2，…，uC]是输入特征单元，表示尺寸为H×W、通道数为C的特征图层。分两个分支传播：通道维度和空间维度。在通道维度中对每个特征通道进行全局池化，得到信道描述符z∈ RC×1×1，如式（2）所示。其中：uC(i，j)表示通道uC第(i，j)位置上的数值，并且使用Sigmoid和线性整流单元（Rectified Linear Unit，ReLU）作为门控机制在传播过程中学习特征通道间的非线性交互，分别用σ(·)和δ(·)表示，如式（3）所示。最后通过fC(·)将信道描述符和特征图相乘得到最终的输出特征UC，如式（4）所示。

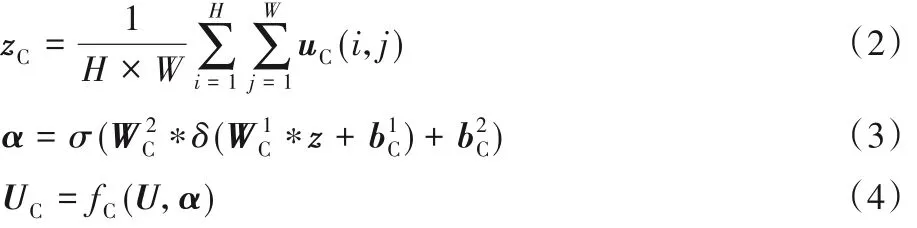
通道维度中使用全局池化将全局的空间信息压缩到信道描述符中，可以对融合天气和航班数据的特征图进行权重分配。

与通道维度互补的空间维度的特征重标定可以更有效地“关注”到局部维度的数据。网络前向结构设计中，将输入特征U经过两层卷积神经网络得到空间标定因子β∈ R1×H×W，第一层卷积产生每层的特征图随后与第二层1*1 卷积神经网络相连接（参数为W2S，b2S）。然后使用 Sigmoid 函数σ(·)对第一层网络产生的特征图元素映射到区间［0，1］中，得到空间标定因子β，如式（5）所示。最后与输入特征U作乘积运算，其中，fS(·)表示将特征图空间位置上的元素与对应的空间标定因子β相乘，如式（6）所示。输入特征经过双重标定后，经过卷 积 层 得 到 最 终 输 出 特 征UO=[u1，u2，…，uC′]，如 式（7）所示。

1.3 网络配置及训练

1.3.1 配置信息

表2 中给出了S0和S1两种网络配置信息，分别表示不同转换层和不同网络结构。其中团簇包含两个网络参数：每个团簇中网络的层数以及每层中卷积核的个数。在团簇中均使用3× 3 的卷积层进行连接，并采用p= 1 的padding 技术以保证特征图在传输过程中维度不变。卷积层在执行前都经过由批 归 一 化（Batch Normalization，BN）［19］、线 性 整 流 单 元（Rectified Linear Unit，ReLU）和卷积层所组成的执行单元。转换层连接在团簇之后，如果没有特殊说明（如“—”），则表示以卷积核为1× 1的卷积层和2 × 2平均池化作为转换层。

表2 网络模型配置信息Tab. 2 Configuration information of network model

1.3.2 网络训练

本次对神经网络的训练采用反向传播（Back Propagating，BP）的方法，即定义标签和预测值之间的误差函数，通过随机梯度下降不断调整网络的权重和偏置，使网络不断拟合目标函数，进而得到学习的目的。反向传播中，主要为梯度值和误差项的计算，梯度由误差项推导得出。以下对CliqueNet 中一个4 层随机连接团簇的实例进行梯度计算推导，如图2 第二阶段。第一阶段进行网络初始化过程，不参与反向传播。首先，依据BP算法［20］计算各隐藏层的误差项以及第l层第i幅特征图的误差项（如式（8）），然后利用误差项公式计算出网络各隐藏层梯度（如式（9））。

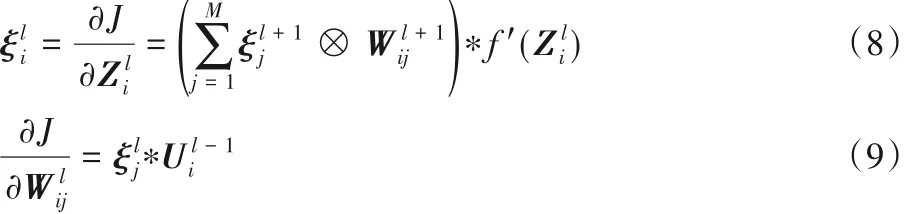
其中：J 表示定义的损失函数；ξl+1i 为第l + 1 层中第i 幅特征图；表示第l + 1 层与第l 层中第i 幅特征图到第j 幅特征图的映射矩阵；表示第l卷积层中第i幅特征图，f′()表示为该层激活函数的导数；“⊗”类似卷积核操作，区别在于它将卷积核进行翻转后再与对应的误差特征作滑动乘积并累加的运算。

同理由式（10）可以逐个求出隐藏层的误差项迭代关系，其中，Ul表示第l 层的输出特征值表示损失函数对输出特征值的导数。结合式（8）～（10）可以得出Stage-Ⅱ的各隐藏层的误差项计算，结果如式（11）～（14）所示。

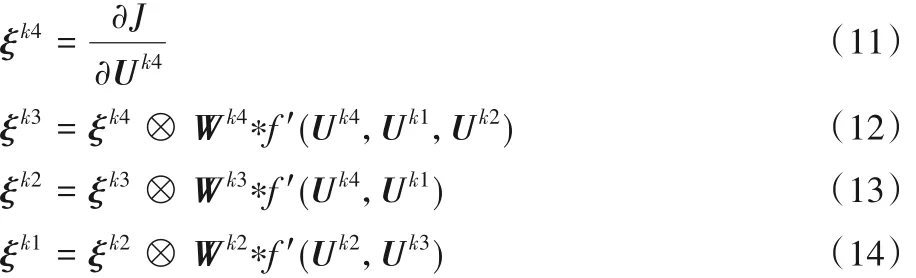
根据式（10）～（14），网络的首个隐藏层梯度值可由式（15）表示，式中U表示输入特征图。

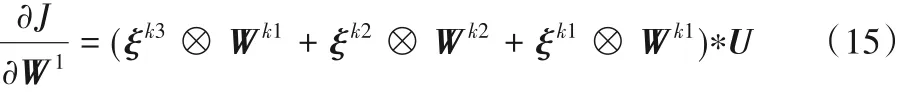
从反向传播的推导过程中可以看出，由于团簇随机连接方式，在计算激活函数导数时，其特征值输入不仅仅来自前面级联网络层，也会随机包含其他网络层传入的特征数值。各隐藏层梯度计算完成之后需要调用随机梯度下降函数，如式（16）所示，以不断更新权重参数，直到网络收敛。

后文中将对梯度值前的系数η（学习率）展开谈论，引入退化学习率，以更好地训练模型。

2 航班延误预测

2.1 预测模型

从航班延误预测模型整体结构（图4）可以直观地看到6层团簇和转换层（Transition）之间的逻辑关系：团簇采用随机连接方式模拟大脑中复杂网络的结构和功能特征［21］。如果类比于神经元，其特征层和信息传递的连接相当于胞核和轴突部分，某种意义上能更好地模拟大脑皮层的电信号交互的方式［22］。本文首先对航班、天气的数据进行融合，然后输入模型进行特征提取，最后给出航班延误程度的预测。

图4 航班延误预测模型整体结构Fig. 4 Overall framework of flight delay prediction model

2.2 数据融合

本文模型使用的实验数据来自于2017—2018 年美国交通运输统计局（Bureau of Transportation Statistics，BTS）的航班数据和美国国家海洋和气候管理局（National Oceanic and Atmospheric Administration，NOAA）提供的本地气候质量监控数据。为了方便叙述，将两块数据集整理为航班数据、机场数据、气象数据三个数据集并给出以下定义：

1）航班数据：F ={ f1，f2，…，fl，…，fn1}，其中：f1表示单个样本，即一条航班数据；n1 表示样本总量（以下类似）。每条样本主要包括起飞日期、航空公司ID、起飞/降落机场ID、起飞/降落城市代码、起飞/降落城市ID、航班号、计划起飞/降落时间、滑出时间、起轮/放轮时间、滑入时间等27个特征。

2）机场数据：A ={a1，a2，…，al，…，an2}。本文主要针对起飞延误作数据分析，机场数据选取自延误影响较大的机场，每条样本包括日期、起飞延误时长、机场ID、机场代码、机场所在航空区域等8个属性特征。

3）气象数据：W ={w1，w2，…，wl，…，wn3}，包括日期、具体观测时间、气象观测站类型/所在机场、机场天气状态、天空状况、风向、风速、能见度、温度、相对湿度、海平面气压、海拔高度等19个特征。

对数据清洗是整个预处理过程中必不可少且较为重要的环节。上述数据集的异常数据主要包括异常值和缺省值两类。本文针对异常值使用SQL 语句直接进行删除；而针对较少比例的缺省值则直接采用均值进行填充。数据集中涉及改航班和取消航班两个维度数据缺省率达到95%以上，考虑到这两个特征对延误的影响不是很大，后期对这两个维度数据直接进行了删除。

数据融合部分主要目的是为了让三个数据集建立关联，为保证时空一致性，在空间维度上通过机场ID、航班起飞/到达机场ID和观测站所在机场ID进行关联，并通过各个数据集的时间戳进行关联以确保三部分的数据集保持时间上的一致性。具体操作步骤如下所示：

1）读入航班数据F、机场数据A、天气数据W。

2）读取一条航班数据f，对机场ID、日期/时间设置关联键值，得到flight_key，f。

3）读取一条机场数据a，对起飞/到达机场ID、计划起飞/降落时间设置关联键值，得到airport_key，a。

4）读取一条天气数据w，对各观测站所在机场ID、观测时间设置关联键值，得到weather_key，w；

5）将上述数据中具有相同key的数据执行merge 操作，即相同主键的数据进行连接，得到融合后的数据集r。

6）将融合后的数据集r逐条取出，对每条数据中连续特征字段通过Min-Max 归一化编码方式将数据映射到［0，1］区间，消除量纲之间的差异；对于高基数离散字段按照数据出现频次使用Mean-Encoder 进行编码。构建输出矩阵R，本次实验使用航班数据共1 505 056 条，编码后为81 维特征，最终通过矩阵变换输入到神经网络中的数据维度为1505 056 × 9 ×9。

2.3 分类预测

首先，按照表3 中延误时间对航班延误等级［23］进行判定划分，共5 个等级，并对其进行One-hot 编码，作为标签值。然后，矩阵R经过模型特征提取后，由分类预测模块对其作分类预测处理。提取的最终特征由全局池化层将维度大小为n×n×c的矩阵转换为一维向量V=[v1，v2，…，vc]，全连接后经过Softmax 分类器［24］，即将V映射成延误等级预测的一维概率向量si，如式（17）所示。最后对预测的一维向量取对数并与标签值{y(i)=j}作交叉熵运算作出判定，如式（18）所示，即得到向量空间中两个向量空间的距离，并根据结果中距离最近判定预测结果是否准确。

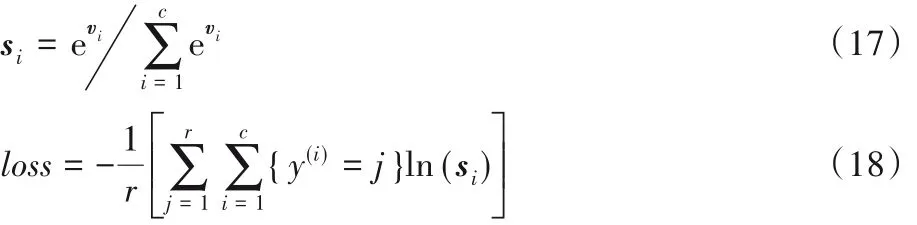
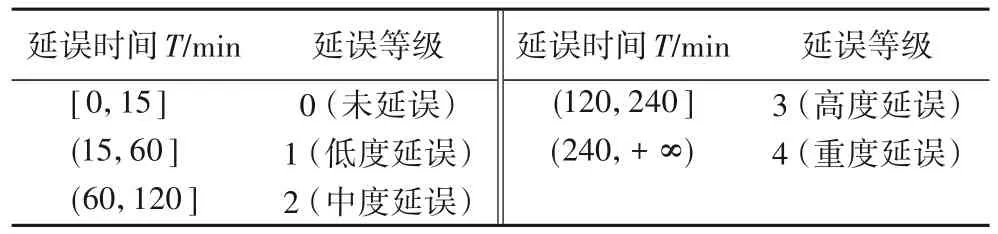
表3 航班延误等级划分Tab. 3 Classification of flight delay level

2.4 航班延误预测的混淆矩阵

航班延误的混淆矩阵如表4 所示，其中每一列代表了数据的真实归属类别，每一行表示实际的预测结果值；T、F 分别表示正确和错误的预测结果，预测值与标签值一致时判定为正确，否则判定为错误。例如，分类器会给出某条航班数据属于 5 个 类 别 的 概 率 分 别 为［0.979 494 6，0.013 817 06，0.000 327 83，0.000 306 73，0.006 053 79］，分类器会选择概率最大值作为输出类别，以此判定该航班的延误等级，所以该例为未延误。测试中若与航班延误时间划分的未延误标签值［1，0，0，0，0］一致，则判定正确，否则错误。实际航班延误分析数据量较大，后文实验中使用混淆矩阵中二级指标准确率来衡量模型。

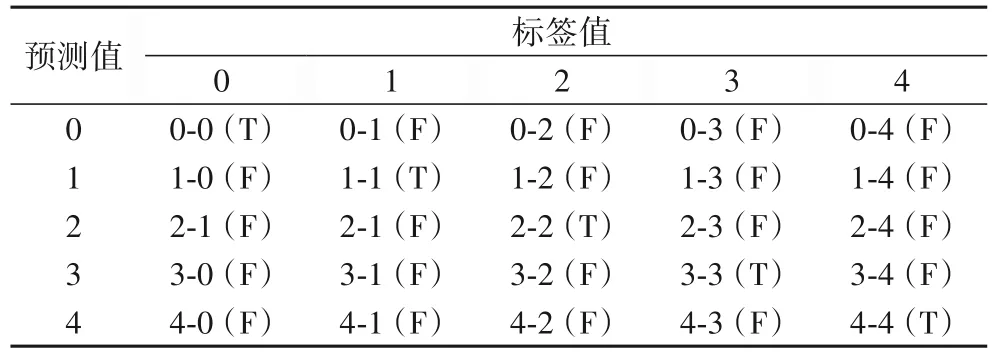
表4 航班延误预测的混淆矩阵Tab. 4 Confusion matrix of flight delay prediction

3 实验结果与分析

本章主要对实验中的硬件环境、模型网络的超参数配置，以及CliqueNet 的不同网络结构对实验结果产生的影响进行阐述，最后对不同的模型给予比较。

3.1 实验环境和参数配置

实验室硬件配置了2 台工作站，3 台高性能服务器：戴尔工作站是 Intel Xeon Sliver 4114 CPU，主频 2.20 GHz，10 核，NVIDIA TITAN Xp GPU，12 GB 显存；戴尔 PoweredgeR730 机架式服务器，Intel XeonE5-2630 双 CPU，16 GB 内存，1 TB SAS，NVIDIA TESLA P100 GPU。 软 件 运 行 环 境 为Ubuntu16.04操作系统搭建的Tensorflow深度学习框架。

本文对超参数设置如下：L2 正则化系数［25］为 0.000 1，Dropout［26］比例 0.85，可以有效防止过拟合，使用交叉熵作为损失函数，并采用随机梯度下降（Stochastic Gradient Descent，SGD）［27］的方法加快函数收敛。训练批次大小设置为128，默认设置为2的倍数。

3.1.1 退化学习率

为在训练速度和精度之间找到平衡，对随机梯度下降优化器第一个超参数学习率η进行讨论。较大学习率会使训练速度会有所提升，但是损失函数不能很好地收敛至最小值，存在较大的波动；过小的学习率会使精度有所提升，但是训练会耗费太多时间。因此，引入退化学习率，即对学习率进行批次衰减，兼具上述优点，以更好地训练模型。如式（19）所示，其中：ηi表示初始学习率，ηi+1表示退化后的学习率；k表示衰减率，指数g_step表示当前迭代次数，d_step为自定义的衰减步数。

即随着迭代次数的增加，学习率会按照指定衰减率衰减。表5 中，选取初始学习率浮点数后一位、后两位一共四组典型数据进行比较，可以看出初始学习率设置为0.1 时，实验结果较为理想，所以本文后续实验中将初始学习率设置为0.1。

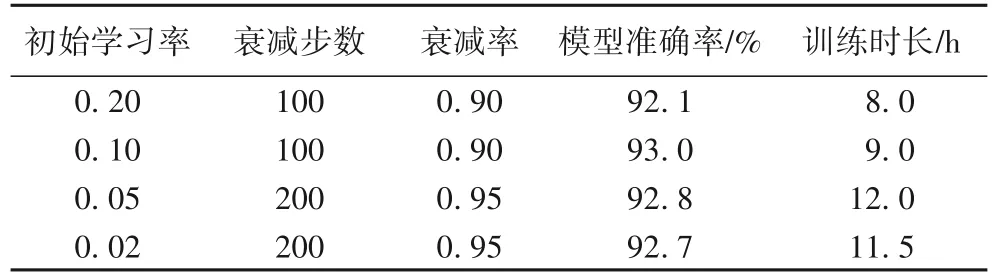
表5 初始学习率对模型准确率与训练时长的影响Tab. 5 Effect of initial learning rate on modelaccuracy and training duration

3.1.2 数据均衡和分类准确率

本次训练使用的航班延误数据量较大，可达到百万级，各延误等级之间的数据样本数目差距很大，考虑到实验中的数据不均衡问题，在转换成输入矩阵时对样本进行重采样：通过上采样增加延误航班类别的数据条目，对正常航班采用下采样以减少样本数量，来适当地改变样本的分布。但是实际生活中的正常航班和延误航班数目差距很大，尤其是表3 中重度延误情况，即使使用数据均衡，其数据占比仍然相差较大，但考虑其仍然符合实际的期望，故使用重采样后的数据集作为训练样本，具体信息如表6 所示。训练使用的测试数据集在每种分类中按照1/10的比例随机挑选。

分类预测准确率p表示预测结果正确（即与标签值保持一致）的航班样本与样本总量的比值：

其中：N表示样本总量，q为延误等级数，Pi表示实际延误等级为i的航班样本中被预测正确的航班数据条数。

3.2 不同团簇连接对结果的影响

表7 给出了团簇中不同的连接方式在数据集r上测试的准确率，其中：R-conn 表示随机连接（Random connection），F-conn 表示全连接（Full connection），Ⅰ-Ⅱ表示Stage-Ⅰ的特征传递给损失函数，Stage-Ⅱ的特征由转换层传入到下一个团簇（如图4 所示）。从表7 和图5 中可以看出，R-conn-Ⅱ-Ⅱ准确率为92.9%，比F-conn-Ⅱ-Ⅱ高0.5 个百分点，训练时的损失值维持在0.172 左右，比全连接更低，这说明随机连接在减少连接的同时，网络性能依然趋于稳定。R-conn-Ⅰ-Ⅱ的准确率也一直保持在92.0%左右，可以看出团簇随机连接依然保持了较高的预测准确率。

表7 不同团簇连接的预测准确率比较Tab. 7 Comparison of prediction accuracy of different clique connections

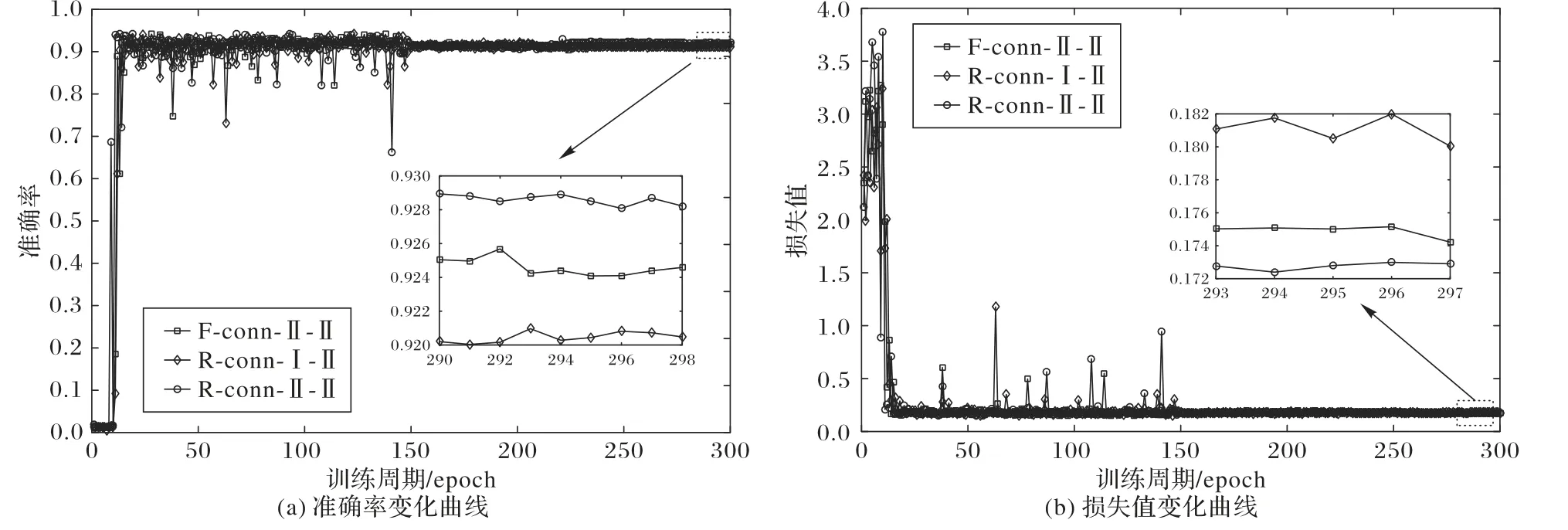
图5 不同团簇连接方式实验结果变化曲线Fig.5 Variation curves of experimental results for different clique connections

3.3 不同转换层对实验结果的影响

图6 和表8 是团簇之间不同转换层的实验结果比较。如1.2 节所述，CSAR 模块分别对通道维度和空间维度作出特征标定，如图6（a）所示，与SE模块只对通道维度作出标定相比，CSAR 模块最后的预测分类准确率要高出0.9 个百分点。嵌入不同的转换层对网络的复杂程度及参数量的增长几乎可以忽略不计，在训练过程中，损失值表示预测数值和真实值接近程度，损失值越小表示越接近真实值。从图6（b）和表8 中可以看出，引入CSAR 模块将网络损失值减小至0.17 左右并趋于稳定，表示网络拟合度刚好，没有出现过拟合和欠拟合的现象，这说明对转换层进行改进可以更好地训练模型。对比表8和表7的数据可以看出，预测准确率均有所提升，其中CSAR模块的引入将网络最终准确率维持在93.4%左右。

3.4 不同模型比较

为了验证基于大数据的深度学习方法比传统的机器学习统计算法更具优势，表9 中给出了不同航班延误预测模型的准确率结果。其中：贝叶斯网络［3］和支持向量机［5］分别以国内的某枢纽机场和某航空公司提供的整年数据进行训练，但其只涉及单独的机场和航班数据，数据维度较小。ANN 模型［8］以2012 年肯尼迪机场的1 099 次入境航班作数据分析研究，数据样本量较少。并行化随机森林［6］特征划分的数据来源于美国航空交通运输统计局2015—2016 年的历史数据，使用的数据源和本文保持一致。随机森林模型［7］使用来自2007 年1月份至2008年12月份航空系统性能度量数据库的数据，其数据字段和本文分析的字段相似，包括到达和离开机场、计划和实际起飞时间、航空公司代码和飞机尾号等。双通道卷积神经网络（Dual Channel Neural Network，DCNN）［28］与本文使用的数据集相同，样本数量均为150 万左右。除此之外，卷积神经网络DenseNet 同样属于密集型连接网络，与本文模型的可比性较强，所以本文实验在相同的数据集上给出了两者在不同量级网络的预测结果比较（见表9，其中：T表示网络卷积层数，k表示每层的卷积核个数）。

表 9 中同时还给出了在 CIFAR-10 数据集［29］上进行测试的结果。CIFAR-10 是图片分类中常用的测试数据集，共60 000 张大小为32 × 32的图片集。相较于传统的模型算法，随机连接的CliqueNet 性能有明显的提升。其中CliqueNet 仅用了12 层网络就获得了与96 层DenseNet 几乎一致的准确率，说明网络的连接方式更为高效，以轻量级网络实现了较高的准确率。

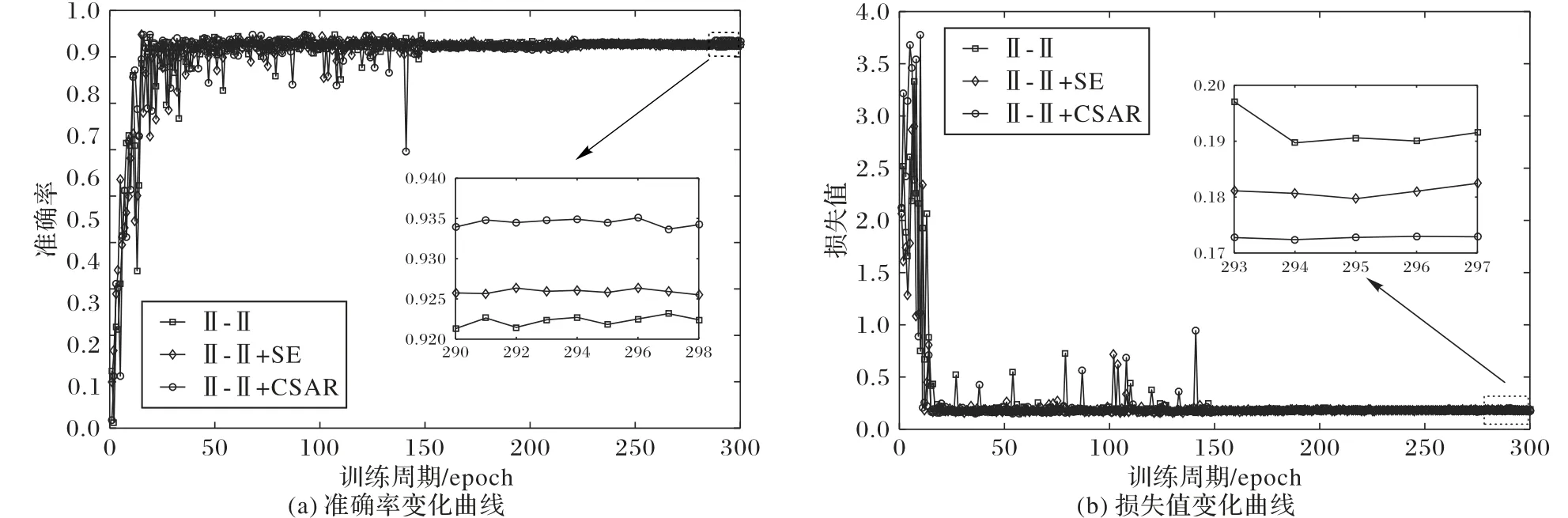
图6 不同转换层实验结果变化曲线Fig.6 Variation curves of experimental results for different transition layers

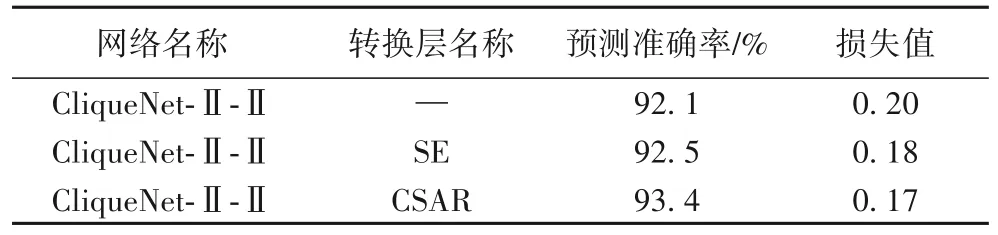
表8 不同转换层的预测准确率比较Tab. 8 Comparison of prediction accuracy of different transition layers

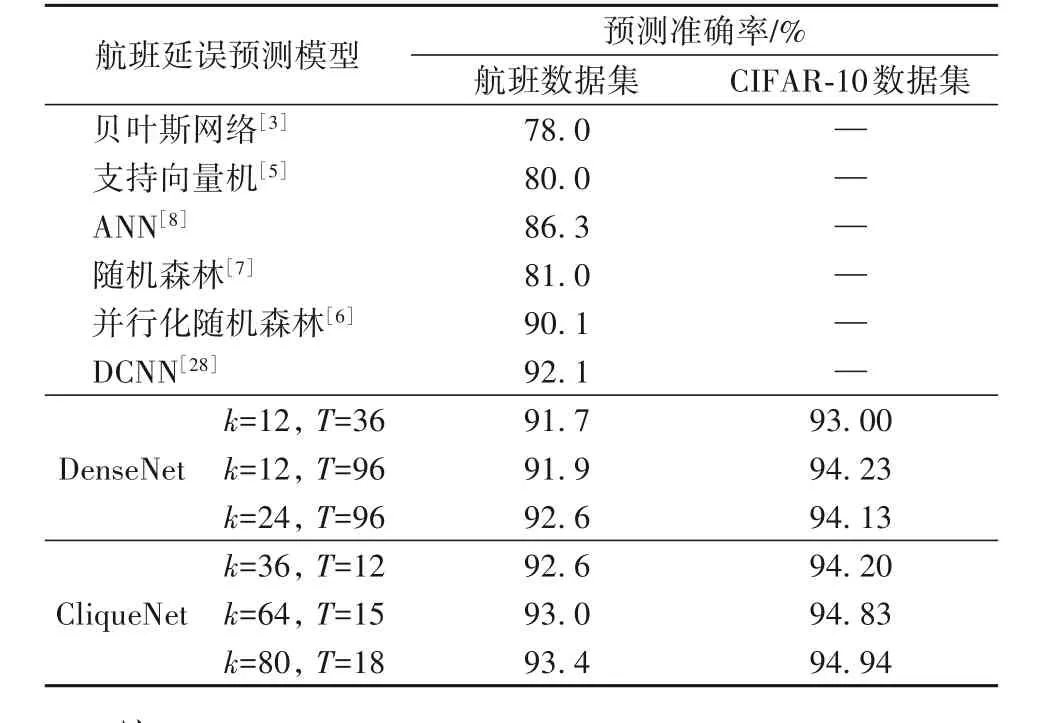
表9 不同航班延误预测模型的准确率比较Tab. 9 Accuracy comparison of different flight delay prediction models

4 结语

本文提出了一种团簇随机连接的CliqueNet 航班延误预测模型，以随机密集型连接方式更为有效地让网络之间进行信息流动，以轻量级网络获得了高精度的航班延误预测准确率；并且对不同的转换层进行讨论，对通道和特征维度进行特征重标定，使预测准确率最多提升约1 个百分点。为存储海量数据，实验室中搭建了HDFS（Hadoop Distribute File System）［30］为基础的大数据平台。神经网络模型训练可以充分利用大数据的优势，让网络在充分的资料学习基础上挖掘数据背后的客观规律，进而达到高精度预测的目的。本实验室于2019 年与华东空管局有围绕航班延误预测展开的项目合作。其中华东空管局提供了2018年3月到2019年3月的国内航班和气象数据，正在进行相关数据预处理工作，后期工作重点主要放在国内数据的研究和分析。